2023NOIP A层联测20-旅行
小 A 旅行到了远方的一座城市,其内部的道路可以被视为一张包含恰好 n n n 个点以及 n n n 条边的无向连通图。这里的居民可以用一种特质的墨水来改变图中某一条边的颜色。
居民们的狂欢节即将开始了,且节日会持续 m m m 天。每一天,居民们会选择图中的一条边,并用某一种颜色的墨水去覆盖这条边原有的颜色。在每一天的最后,他们都想知道当前的城市包含多少个颜色相同的连通块。
特别的,一个颜色相同的连通块指的是一个由一些相同颜色的边组成的连通块。
多组数据 T ≤ 10 T\le10 T≤10
n , m ≤ 1 0 5 n,m\le10^5 n,m≤105
首先这个图是基环树。
可以用各种方法求出一开始颜色相同连通块的个数。我使用并查集。
对于每次询问,改变这条边的颜色,贡献只需看两个点的连边情况。
可以分成两部分考虑,先去掉这条边的颜色,再加上修改的颜色。
前一个操作,如果两边都有这种颜色,那么断掉这条边会增加一个连通块;如果两边都没有,就会减少一个;否则不变。
后一个操作,如果两边都有这种颜色,那么断掉这条边会减少一个连通块;如果两边都没有,就会增加一个;否则不变。
但是如果两边的颜色是同一个连通块,那么就不会增加连通块,这种情况只能是环上的边全是一种颜色(在后种情况就是除了当前边全是一种颜色),特判即可。
实现上可以开 n n n 个 map 维护当前点的出边颜色。
时间复杂度 O ( T n log n ) O(Tn\log n) O(Tnlogn)
代码如下
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+1;
int n,m,fa[N],bj[N],dfn[N],low[N],num,vis[N],VIS[N];
stack<int> s;
vector<int> ans;
map<int,int> ma[N],ring;
map<pair<int,int>,int> To;
struct Node
{int v,w,id;Node(){}Node(int a,int b,int c){v=a,w=b,id=c;}
};
vector<Node> v[N];
struct node
{int u,v,w;bool operator==(const node &a)const{return u==a.u&&v==a.v&&w==a.w;}
}a[N];
int find(int x)
{return x==fa[x]?x:fa[x]=find(fa[x]);
}
void add(int x,int y)
{int a=find(x),b=find(y);if(a!=b) fa[a]=b;
}
void dfs(int u,int fa)
{dfn[u]=low[u]=++num;s.push(u);for(auto i:v[u]){if(!dfn[i.v]){dfs(i.v,u);low[u]=min(low[u],low[i.v]);if(low[i.v]>=dfn[u]){vector<int> aa;int x=0;do{x=s.top();s.pop();aa.push_back(x);}while(x!=i.v);aa.push_back(u);if(aa.size()>2) ans=aa;}}else if(i.v!=fa) low[u]=min(low[u],dfn[i.v]);}
}
void Dfs(int u,int fa)
{if(VIS[u]) return;VIS[u]=1;for(auto i:v[u]) if(i.v!=fa&&vis[i.v]) ring[i.w]++,Dfs(i.v,u);
}
int main()
{freopen("tour.in","r",stdin);freopen("tour.out","w",stdout);int t;cin>>t;while(t--){memset(VIS,0,sizeof(VIS));memset(vis,0,sizeof(vis));memset(dfn,0,sizeof(dfn));memset(low,0,sizeof(low));num=0;while(s.size()) s.pop();To.clear();ans.clear();ring.clear();scanf("%d%d",&n,&m);for(int i=1;i<=n;i++) fa[i]=i;for(int i=1,x,y,w;i<=n;i++){scanf("%d%d%d",&a[i].u,&a[i].v,&a[i].w);if(a[i].u>a[i].v) swap(a[i].u,a[i].v);v[a[i].u].push_back(Node(a[i].v,a[i].w,i));v[a[i].v].push_back(Node(a[i].u,a[i].w,i));ma[a[i].u][a[i].w]++;ma[a[i].v][a[i].w]++;To[make_pair(a[i].u,a[i].v)]=i;}dfs(1,0);for(auto i:ans) vis[i]=1;if(ans.size()) for(auto i:v[ans.front()]) if(vis[i.v]){Dfs(ans.front(),i.v);break;}for(int i=1;i<=n;i++){for(auto j:v[a[i].u]){if(j.v==a[i].v) continue;if(j.w==a[i].w) add(i,j.id);}for(auto j:v[a[i].v]){if(j.v==a[i].u) continue;if(j.w==a[i].w) add(i,j.id);}}for(int i=1;i<=n;i++) bj[i]=find(i);sort(bj+1,bj+1+n);int num=unique(bj+1,bj+1+n)-bj-1;for(int i=1,x,y,w;i<=m;i++){scanf("%d%d%d",&x,&y,&w);if(x>y) swap(x,y);int id=To[make_pair(x,y)];int fl1=0,fl2=0;ma[a[id].u][a[id].w]--;ma[a[id].v][a[id].w]--;fl1=ma[a[id].u][a[id].w];fl2=ma[a[id].v][a[id].w];ma[a[id].u][a[id].w]++;ma[a[id].v][a[id].w]++;if(fl1&&fl2&&(!vis[a[id].u]||!vis[a[id].v]||ring.size()>1)) num++;else if(!fl1&&!fl2) num--;ma[a[id].u][a[id].w]--;ma[a[id].v][a[id].w]--;if(vis[a[id].u]&&vis[a[id].v]) ring[a[id].w]--;if(!ring.count(a[id].w)) ring.erase(a[id].w);if(!ma[a[id].u][a[id].w]) ma[a[id].u].erase(a[id].w);if(!ma[a[id].v][a[id].w]) ma[a[id].v].erase(a[id].w);a[id].w=w;ma[a[id].u][a[id].w]++;ma[a[id].v][a[id].w]++;if(vis[a[id].u]&&vis[a[id].v]) ring[a[id].w]++;fl1=0,fl2=0;ma[a[id].u][a[id].w]--;ma[a[id].v][a[id].w]--;fl1=ma[a[id].u][a[id].w];fl2=ma[a[id].v][a[id].w];ma[a[id].u][a[id].w]++;ma[a[id].v][a[id].w]++;if(vis[a[id].u]&&vis[a[id].v]){ring[a[id].w]--;if(!ring.count(a[id].w)) ring.erase(a[id].w);}if(fl1&&fl2&&(!vis[a[id].u]||!vis[a[id].v]||ring.size()>1)) num--;else if(!fl1&&!fl2) num++;if(vis[a[id].u]&&vis[a[id].v]) ring[a[id].w]++;printf("%d\n",num);}for(int i=1;i<=n;i++) v[i].clear(),ma[i].clear();}
}
相关文章:

2023NOIP A层联测20-旅行
小 A 旅行到了远方的一座城市,其内部的道路可以被视为一张包含恰好 n n n 个点以及 n n n 条边的无向连通图。这里的居民可以用一种特质的墨水来改变图中某一条边的颜色。 居民们的狂欢节即将开始了,且节日会持续 m m m 天。每一天,居民们…...
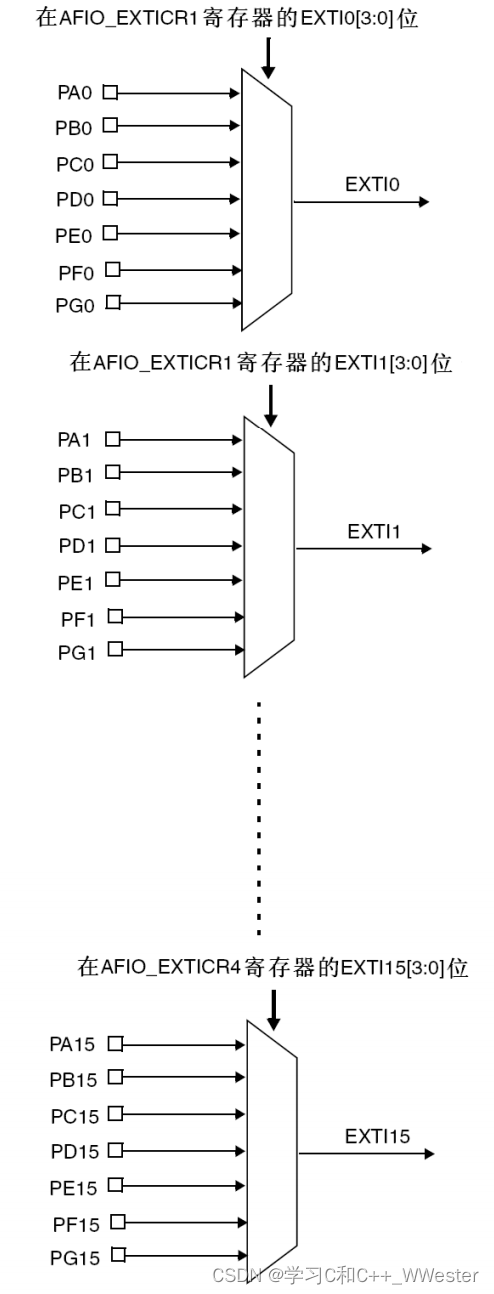
STM32 中断NVIC详解,配置及示例
NVIC全称 Nested Vectored Controller 嵌套向量中断控制器 它是一种硬件设备,用于管理和协调处理器的中断请求。NVIC可以管理多个中断请求,并按优先级处理它们。当一个中断请求到达时,NVIC会确定其优先级并决定是否应该中断当前执行的程序&am…...

10.30英语期中稿
influence of Chinese and Japanese literary culture on the country and the world, and compare the differences between the two 对自己文化影响 中日文学文化比较 表达,餐饮,服装 相似点与不同点 与日本友人交流 draft Chinese and Japanes…...

二维数组如何更快地遍历
二维数组如何更快地遍历 有时候,我们会发现,自己的代码和别人的代码几乎一模一样,但运行时间差了很多,别人是 AC \text{AC} AC,你是 TLE \text{TLE} TLE,这是为什么呢? 一个可能的原因是数组的…...
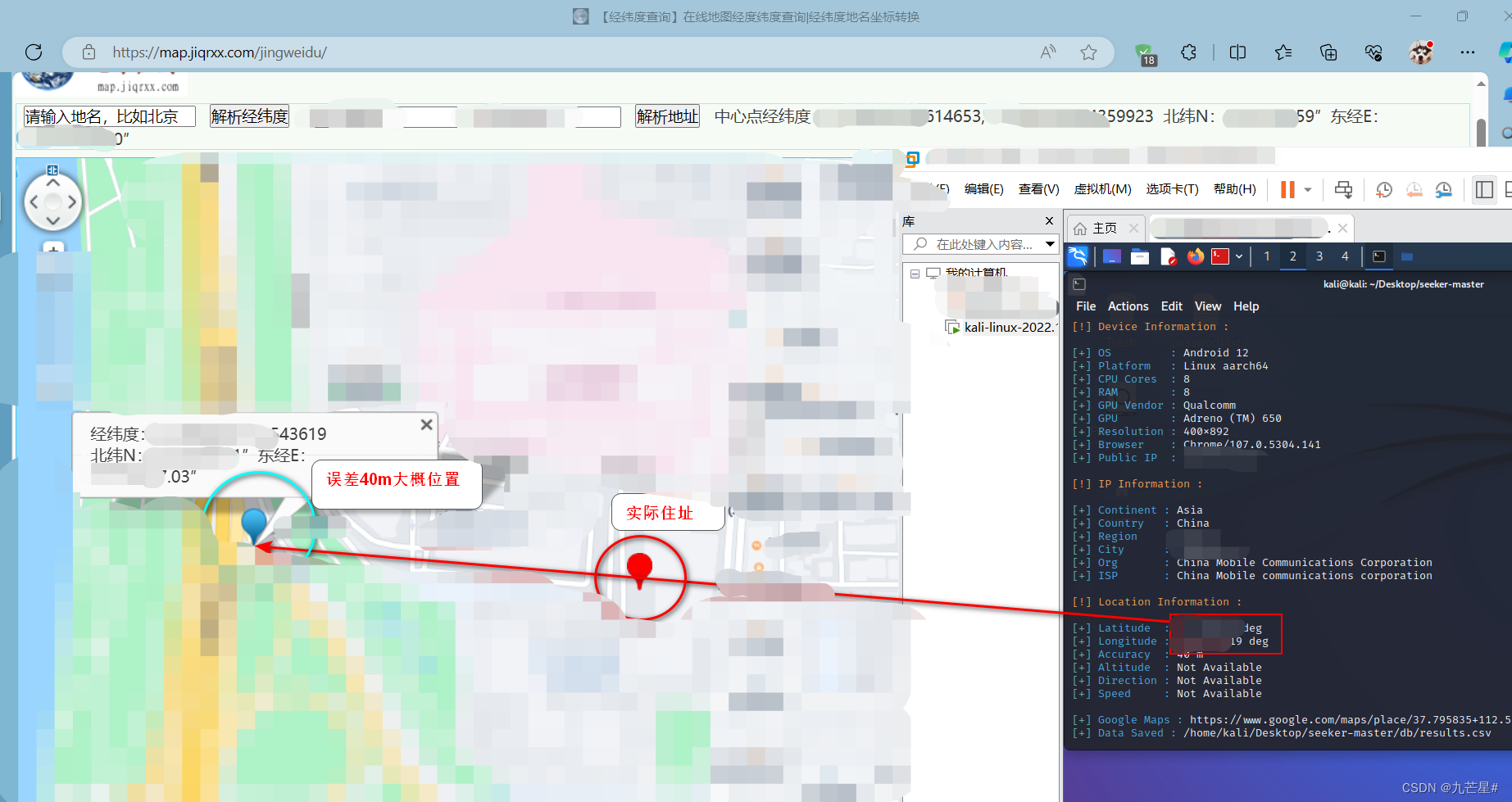
【网络安全】Seeker内网穿透追踪定位
Seeker追踪定位对方精确位置 前言一、kali安装二、seeker定位1、ngrok平台注册2、获取一次性邮箱地址3、ngrok平台登录4、ngrok下载5、ngrok令牌授权6、seeker下载7、运行seeker定位8、运行隧道开启监听9、伪装链接10、用户点击(获取定位成功)11、利用经…...
Spring Boot 3系列之一(初始化项目)
近期,JDK 21正式发布,而Spring Boot 3也推出已有一段时间。作为这两大技术领域的新一代标杆,它们带来了许多令人振奋的新功能和改进。尽管已有不少博客和文章对此进行了介绍,但对于我们这些身处一线的开发人员来说,有些…...

用python判断一个数是否为素数
判断一个数是否为素数可以使用以下方法: 排除特殊情况:首先判断该数是否小于等于1,因为素数定义中,素数必须大于1。如果小于等于1,则该数不是素数。 除尽法(试除法):从2开始&#x…...

FreeRTOS_信号量之二值信号量
目录 1. 信号量简介 2. 二值信号量 2.1 二值信号量简介 2.1.1 二值信号量无效 2.1.2 中断释放信号量 2.1.3 任务获取信号量成功 2.1.4 任务再次进入阻塞态 2.2 创建二值信号量 2.2.1 vSemaphoreCreateBinary() 2.2.2 xSemaphoreCreateBinary() 2.2.3 xSemaphoreCrea…...
使用Gateway解决跨域问题时配置文件不生效的情况之一
首先html文件只有一个发送ajax请求 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" content"IEedge"><meta name"viewport" content&q…...
【火影手游】新版押镖护送高分攻略
文章目录 Part.I IntroductionPart.II 迪达拉视角1、打栅栏2、石头边,打石头和栅栏3、石头边,踩封印,撞力士4、大树前,打石头和栅栏5、石头边,给佩恩当路标6、后一前二接大招7、补伤害 Part.III 佩恩视角1、头进洞&…...
【JVM】类的声明周期(加载、连接、初始化)
🐌个人主页: 🐌 叶落闲庭 💨我的专栏:💨 c语言 数据结构 javaEE 操作系统 Redis 石可破也,而不可夺坚;丹可磨也,而不可夺赤。 JVM 一、类的声明周期(加载阶段…...
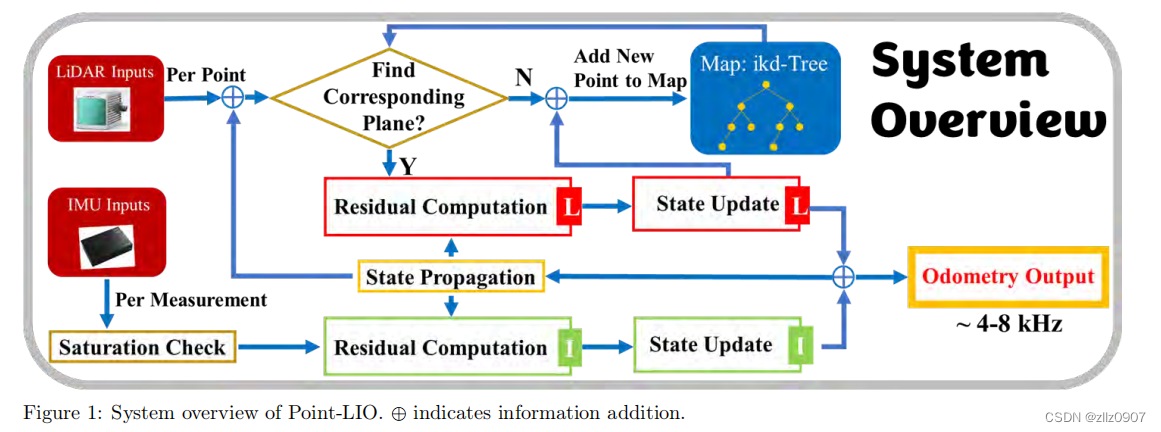
开源3D激光(视觉)SLAM算法汇总(持续更新)
原文连接 目录 一、Cartographer 二、hdl_graph_slam 三、LOAM 四、LeGO-LOAM 五、LIO-SAM 六、S-LOAM 七、M-LOAM 八、livox-loam 九、Livox-Mapping 十、LIO-Livox 十一、FAST-LIO2 十二、LVI-SAM 十三、FAST-Livo 十四、R3LIVE 十五、ImMesh 十六、Point-LIO 一、Cartograph…...

绕WAF手法总结
云锁 被拦截 http://www.test123.com/article.php?id1%20union%20select%201,2,3 绕过 http://www.test123.com/article.php?id-1/*!36000union*//*!36000distinct*//*!36000select*/1,2,user() 360websec 被拦截 http://www.xxx.com.cn/productshow.php?id79 绕过 http:/…...
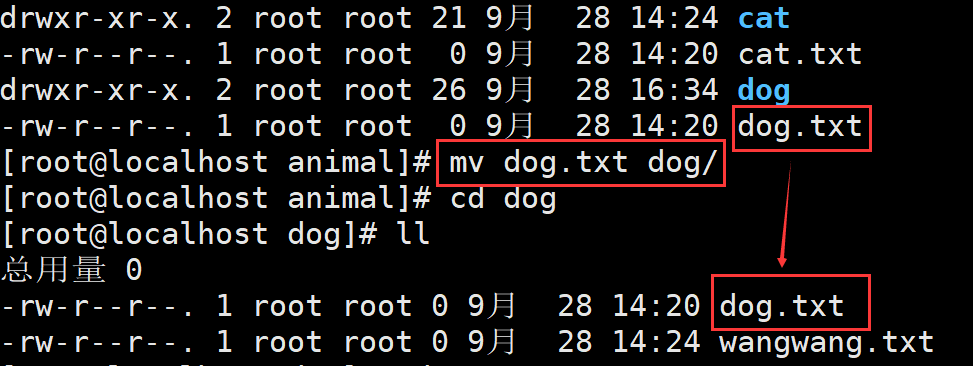
Linux mv命令:移动文件或改名
mv 命令(move 的缩写),既可以在不同的目录之间移动文件或目录,也可以对文件和目录进行重命名。该命令的基本格式如下: [rootlocalhost ~]# mv 【选项】 源文件 目标文件 -f:强制覆盖,如果目标文…...

在 Elasticsearch 中丰富你的 Elasticsearch 文档
作者:David Pilato 对于 Elasticsearch,我们知道联接应该在 “索引时” 而不是查询时完成。 本博文是一系列三篇博文的开始,因为我们可以在 Elastic 生态系统中采取多种方法。 我们将介绍如何在 Elasticsearch 中做到这一点。 下一篇博文将介…...

探营云栖大会:蚂蚁集团展出数字人全栈技术,三大AI“机器人”引关注
一年一度的科技盛会云栖大会将于10月31日正式开幕。30日,记者来到云栖大会展区探营,提前打卡今年上新的“黑科技”。 记者在蚂蚁集团展馆看到,超1亿人参与的亚运“数字火炬手”全栈技术首次公开展示,还可体验基于数字人技术的“数…...
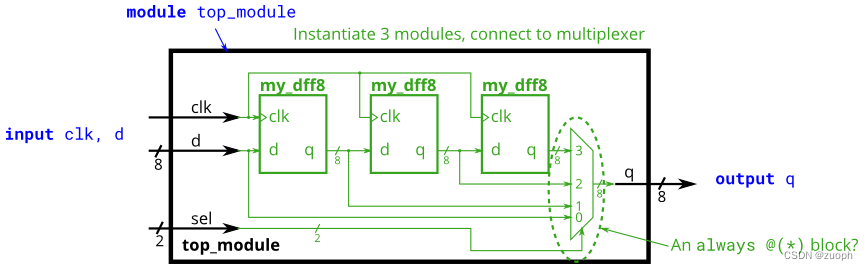
hdlbits系列verilog解答(8位宽移位寄存器)-24
文章目录 一、问题描述二、verilog源码三、仿真结果一、问题描述 这项练习是module_shift移位寄存器的延伸。模块端口不是只有单个引脚,我们现在有以向量作为端口的模块,您将在其上附加线向量而不是普通线网数据。与 Verilog 中的其他位置一样,端口的向量长度不必与连接到它…...
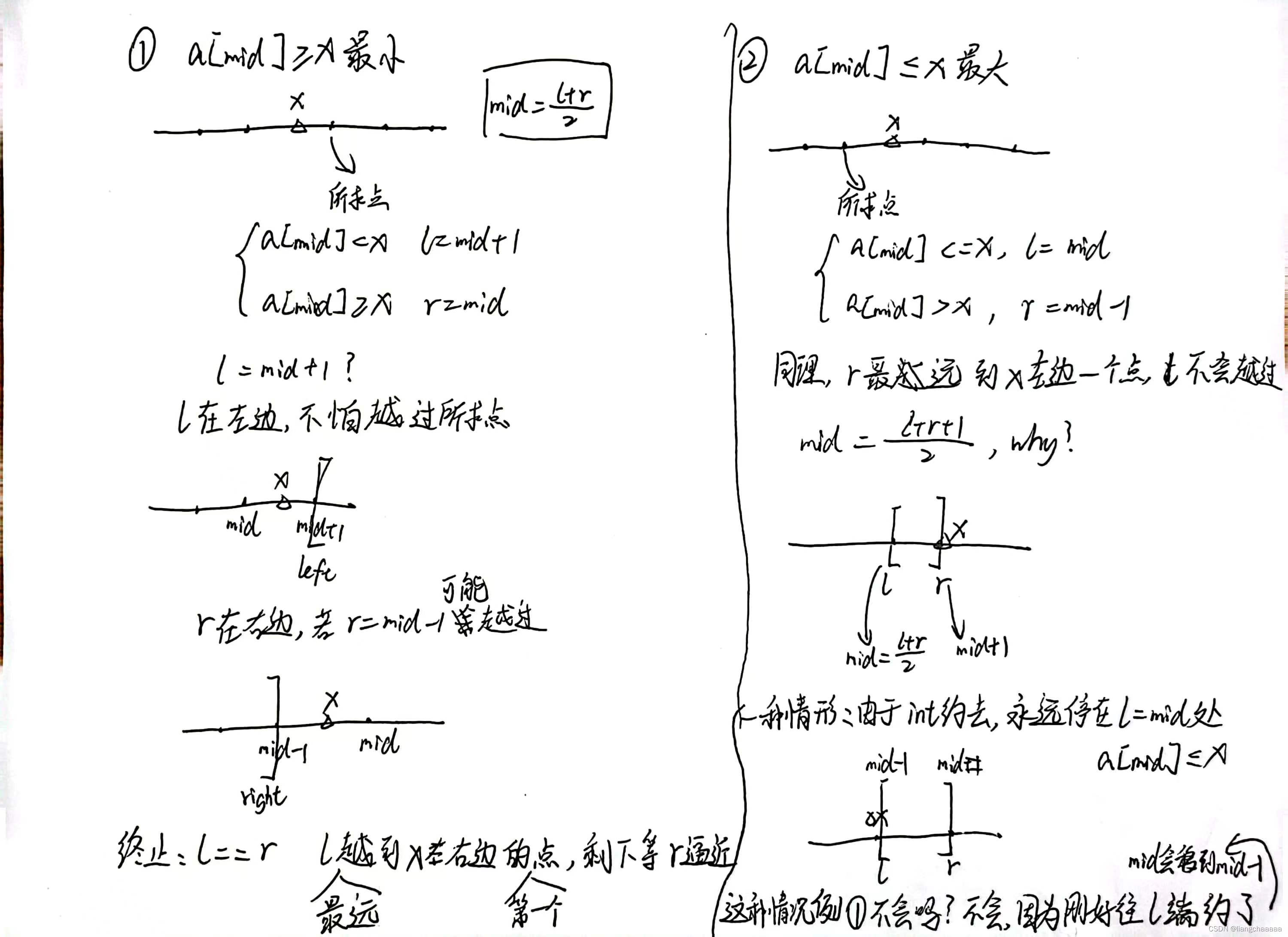
LeetCode 275. H 指数 II
原题链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 题目描述 给你一个整数数组 citations ,其中 citations[i] 表示研究者的第 i 篇论文被引用的次数,citations 已经按照 升序排列 。计算并返回该研究者的 h…...
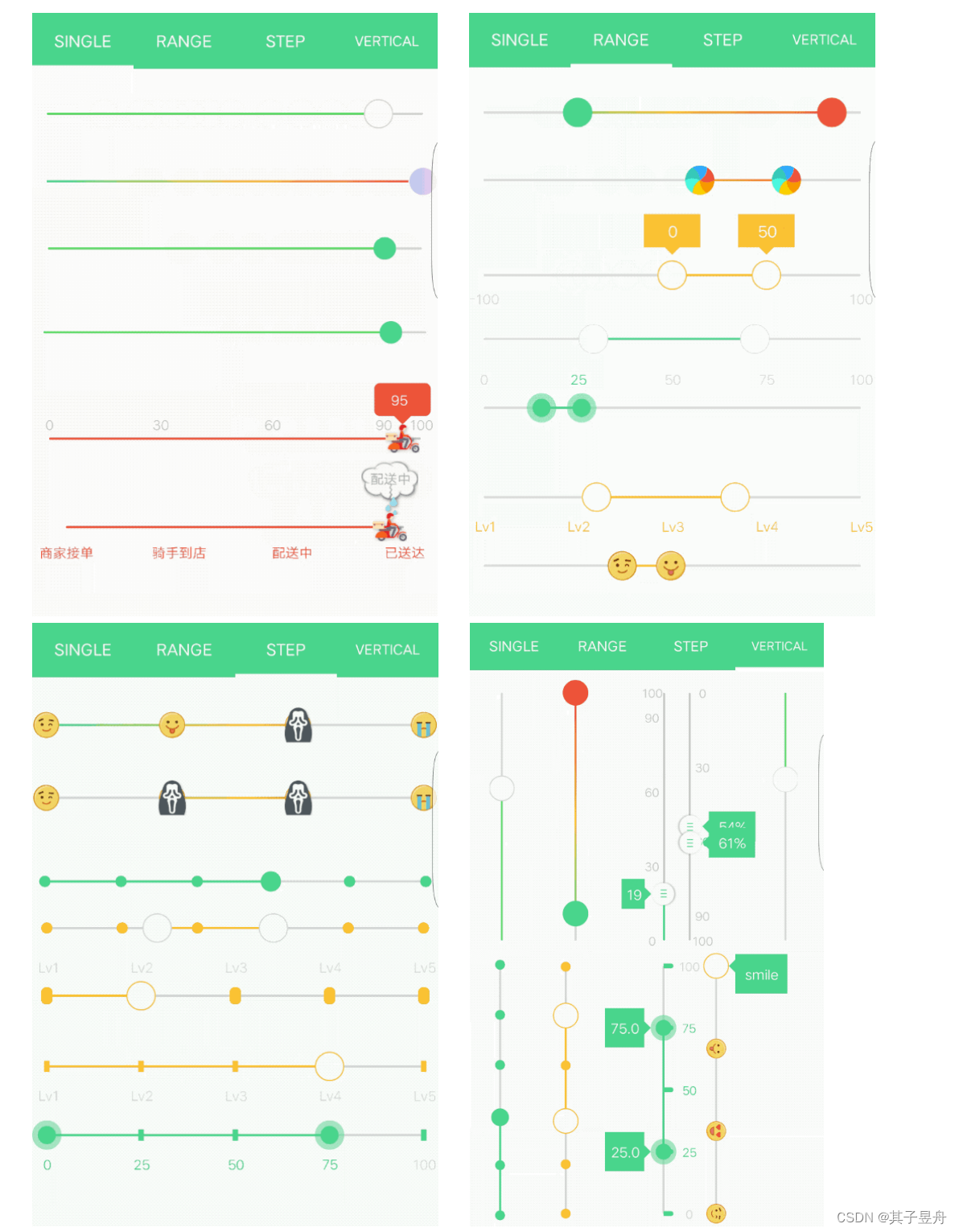
Android 优质的UI组件汇总
1、RuleView :Android自定义标尺控件(选择身高、体重等) 链接:https://github.com/cStor-cDeep/RuleView 2、DashboardView :Android自定义仪表盘View,仿新旧两版芝麻信用分、炫酷汽车速度仪表盘 链接:https://git…...
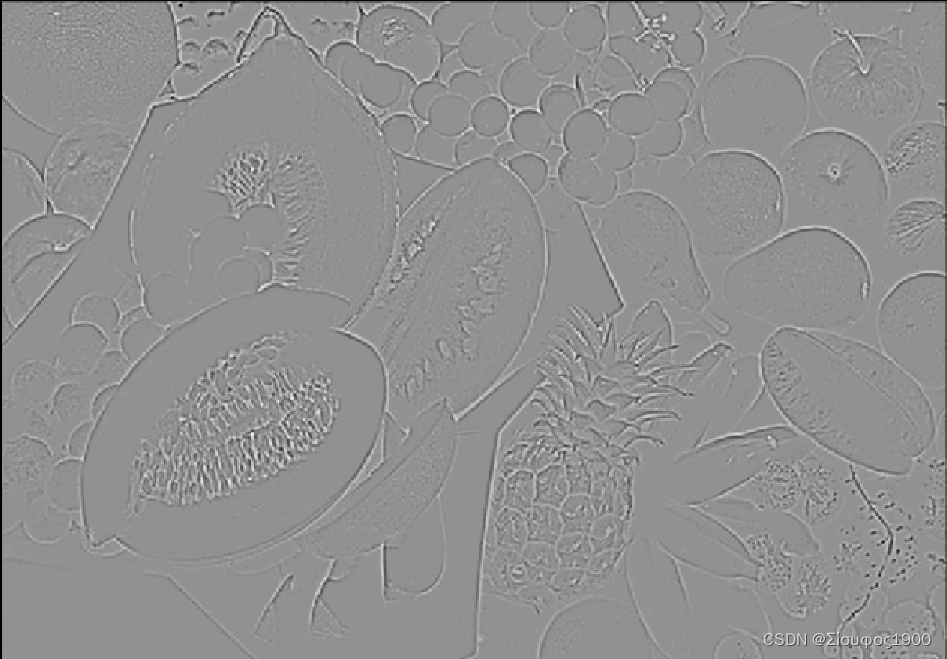
halcon roberts、 prewitt_amp、 sobel_amp、 edges_image、 laplace_of_gauss 对比
原图 灰度: roberts 算子: prewitt算子 sobel 算子 canny算子 拉普拉斯 代码: read_image (Image, C:/Users/alber/Desktop/opencv_images/canny.png) rgb1_to_gray (Image, GrayImage)* 测试 roberts 算子 roberts (GrayImage, ImageRoberts…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...
32单片机——基本定时器
STM32F103有众多的定时器,其中包括2个基本定时器(TIM6和TIM7)、4个通用定时器(TIM2~TIM5)、2个高级控制定时器(TIM1和TIM8),这些定时器彼此完全独立,不共享任何资源 1、定…...
