数据结构与算法:二叉树之“堆排序”
目录
一、树概念及结构
二、二叉树树概念及结构
特殊的二叉树
三、堆的概念及结构
四、堆的创建
1、声明结构体
2、初始化
3、销毁
4、添加新元素
5、交换元素
6、向上调整
7、判断堆是否为空
8、移除堆顶元素
9、向下调整
10、获取堆元素个数
五、使用堆排序
排降序建小堆
完整版:
Heap.h声明部分
Heap.c函数部分
text.c使用及测试部分
一、树概念及结构
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因 为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
- 有一个特殊的结点,称为根结点,根节点没有前驱结点。
- 除根节点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm,其中每一个集合Ti(1 <= i <= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继。
- 因此,树是递归定义的
- 注意:树形结构中,子树之间不能有交集,否则就不是树形结构
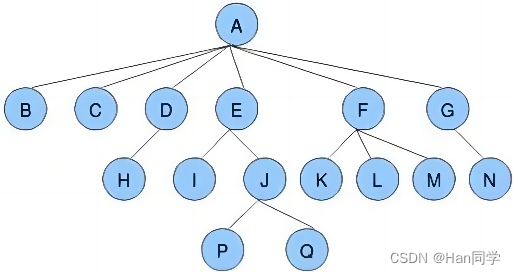
- 节点的度:一个节点含有的子树的个数称为该节点的度; 如上图:A的为6
- 叶节点或终端节点:度为0的节点称为叶节点; 如上图:B、C、H、I...等节点为叶节点
- 非终端节点或分支节点:度不为0的节点; 如上图:D、E、F、G...等节点为分支节点
- 双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图:A是B的父节点
- 孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点; 如上图:B是A的孩子节点
- 兄弟节点:具有相同父节点的节点互称为兄弟节点; 如上图:B、C是兄弟节点
- 树的度:一棵树中,最大的节点的度称为树的度; 如上图:树的度为6
- 节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
- 树的高度或深度:树中节点的最大层次; 如上图:树的高度为4
- 堂兄弟节点:双亲在同一层的节点互为堂兄弟;如上图:H、I互为兄弟节点
- 节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先
- 子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙
- 森林:由m(m>0)棵互不相交的树的集合称为森林;
二、二叉树树概念及结构
二叉树是一个由n(n>=0)个结点构成的有限集合,其中该集合可以为空,这时称其为空二叉树;或者由一个根结点以及两个互不相交的左子树和右子树组成,且左右子树均为二叉树。在二叉树中,子树被明确区分为左子树和右子树,且它们的顺序不可颠倒。
- 值得注意的是,二叉树的定义具有递归性质,因为二叉树本身可以为空,根结点可以有空的左子树或空的右子树。
- 这使得二叉树与普通树有明显的区别,即使只有一棵子树存在,也需要明确指定它是左子树还是右子树。这是二叉树与树最主要的区别之一。
- 请注意,二叉树不同于一般的树,因为它的子树具有左右之分,并且顺序不能颠倒。因此,“二叉树是结点度为2的树”的说法是不正确的。
二叉树的基本形态包括以下五种:
特殊的二叉树
当涉及到二叉树的特殊类型时,有两个主要概念需要了解:满二叉树和完全二叉树。
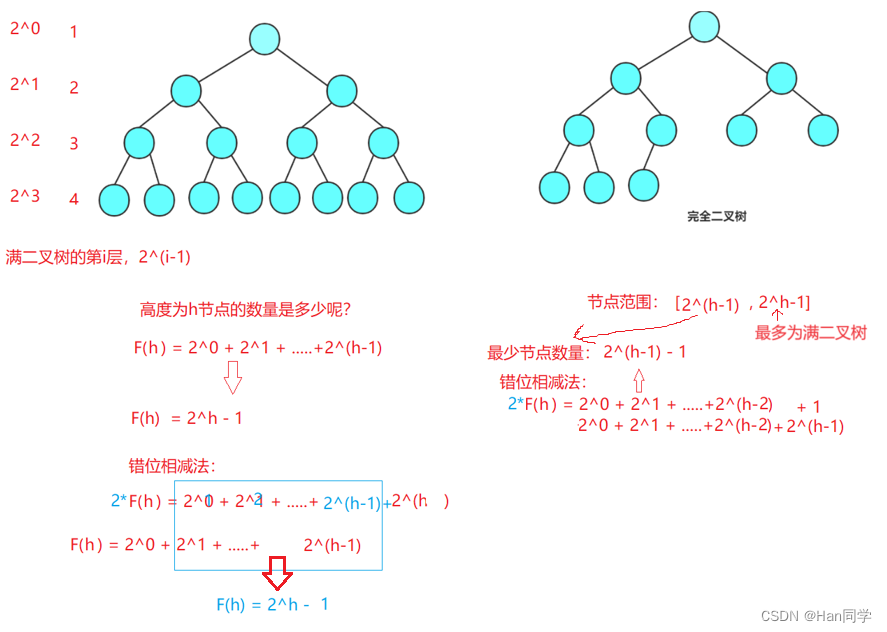
- 满二叉树:满二叉树是一种特殊的二叉树,其特点是每个层级的结点数都达到最大值。具体来说,如果一个二叉树的深度为K,且结点总数为2^K - 1,那么它就是一个满二叉树。满二叉树的每一层都包含最大数量的结点,使得它具有很特殊的结构。
- 完全二叉树:完全二叉树是一种高效的数据结构,与满二叉树相关。一个二叉树如果在深度为K的情况下,其结点都与深度为K的满二叉树中的编号从1到n的结点一一对应,那么它就被称为完全二叉树。需要注意的是,满二叉树是完全二叉树的一个特殊情况。
- 若规定根节点的层数为1,则一棵非空二叉树的第i层上最多有
个结点。
- 若规定根节点的层数为1,则深度为h的二叉树的最大结点数是
。
- 对任何一棵二叉树, 如果度为0其叶结点个数为 n0 , 度为2的分支结点个数为 n2 ,则有 n0 =n2 +1。
- 若规定根节点的层数为1,具有n个结点的满二叉树的深度,h=log以2为底,n+1的对数。
- 对于具有n个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从0开始编号,则对于序号为i的结点有:
- 若i>0,i位置节点的双亲序号:(i-1)/2;i=0,i为根节点编号,无双亲节点
- 若2i+1<n,左孩子序号:2i+1,2i+1>=n否则无左孩子
- 若2i+2<n,右孩子序号:2i+2,2i+2>=n否则无右孩子
三、堆的概念及结构
堆(Heap)是一种特殊的树状数据结构,通常用于实现优先队列和对数据进行排序。堆的主要特点是它是一棵树,其中每个节点的值满足特定的堆属性。在堆中,通常有两种主要类型:最大堆和最小堆。
最大堆(Max Heap):在最大堆中,每个节点的值都不小于其子节点的值,即根节点的值最大。这意味着最大堆的最大元素总是位于根节点,而子树中的值递减。
最小堆(Min Heap):在最小堆中,每个节点的值都不大于其子节点的值,即根节点的值最小。这意味着最小堆的最小元素总是位于根节点,而子树中的值递增。
堆的常见用途包括:
优先队列:堆可以用来实现高效的优先队列,使得可以快速访问和删除具有最高或最低优先级的元素。
堆排序:堆排序是一种高效的排序算法,它利用堆的性质来进行排序。它的时间复杂度为O(n log n)。
堆通常是以数组的形式来表示,其中父节点和子节点之间的关系通过数组索引来建立。具体来说,对于一个具有n个元素的堆,节点的索引从1到n编号,其中:
- 父节点的索引为i,则它的左子节点的索引为2i,右子节点的索引为2i + 1。
- 子节点的索引为i,则其父节点的索引为i/2。
这种数组表示方法使得堆的操作更加高效,因为它不需要使用额外的指针来表示树的结构。
四、堆的创建
本次以小堆举例进行讲解
1、声明结构体
typedef int HPDataType;
typedef struct Heap
{HPDataType* a;int size;int capacity;
}HP;HPDataType被定义为int类型,表示堆中存储的数据类型。- 创建堆的结构体Heap,定义别名为HP。
- 指针a指向堆的数组
- size为堆的当前大小
- capacity为堆的容量
2、初始化
void HeapInit(HP* php)
{assert(php);php->a = NULL;php->size = 0;php->capacity = 0;
}- assert 判断指针是否合法。
- 指向数组的指针 a 初始化为 NULL。
- size 和 capacity 初始化为0。
3、销毁
void HeapDestroy(HP* php)
{assert(php);free(php->a);php->a = NULL;php->capacity = php->size = 0;
}- assert 判断指针是否合法。
- 释放数组空间,将 a 指针置空,同时将 capacity 和 size 设置为0。
4、添加新元素
void HeapPush(HP* php, HPDataType x)
{assert(php);if (php->size == php->capacity) {int newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* tmp = (HPDataType*)realloc(php->a, newCapacity * sizeof(HPDataType));if (tmp==NULL) {perror("realloc fail");return;}php->a = tmp;php->capacity = newCapacity;}php->a[php->size] = x;php->size++;AdjustUp(php->a, php->size - 1);
}- assert 判断指针是否合法。
- 判断当前是否需要扩容,初始堆的容量为0,则为堆开辟四个HPDataType类型大小的空间,如果当前堆的大小size等于容量capacity,则将堆扩容为两倍原来大小的空间。
- 扩容失败,打印错误信息,结束函数
- 将扩容的空间赋值给指针a,更新容量capacity的大小。
- 将要增加的元素插入数组a中,更新size大小。
- 每次在堆中添加新元素时,小堆可能会被破坏,所以我们再添加新元素后,要在AdjustUp函数中判断是否需要进行向上调整。
5、交换元素
后续函数会经常用到,同一串代码放到函数里供其使用者调用比较好。
void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}6、向上调整
void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;while (child > 0) {if (a[child] < a[parent]) {Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else {break;}}
}- 首先通过当前的孩子节点child找到父节点parent。
- 当child大于0时,进行判断当前chilid是否需要调整
- 如果child位置元素小于parent位置元素,则通过Swap进行交换,然后新的孩子节点更新为parent位置,通过孩子节点更新新的父节点位置,然后继续比较和交换,直到不再需要交换为止。
- 如果当前孩子节点不小于当前的父节点,则结束循环,当前节点不需要向上调整。
7、判断堆是否为空
bool HeapEmpty(HP* php)
{assert(php);return php->size == 0;
}8、移除堆顶元素
一般来说,堆的移除操作通常是移除堆顶元素,这样大堆小堆的性质保持不变,如果移除堆底会破坏堆的性质。
void HeapPop(HP* php)
{assert(php);assert(!HeapEmpty(php));Swap(&php->a[0], &php->a[php->size - 1]);php->size--;AdjustDown(php->a, php->size, 0);
}- assert 判断指针是否合法。
- 检查堆是否为空,为空则报错。
- 移除堆顶元素有两种方法,首选第二种方法,不需要重新建堆,节约时间。

- 首先交换堆顶堆尾,然后size减一完成删除,后续不会访问删除位置的元素,所以不释放内存空间也可以。
- 然后进行向下调整。
9、向下调整
向下调整是从第一个节点(父节点)开始向下调整,传入参数命名为parent
void AdjustDown(HPDataType* a, int size, int parent)
{int child = parent * 2 + 1;while (child < size) {if (child + 1 < size && a[child + 1] < a[child]) {child++;}if (a[child] < a[parent]) {Swap(&a[child], &a[parent]);parent = child;child = parent * 2 - 1;}else {break;}}
}- 通过传入参数获取到当前的左子节点的位置。
- 当child位置小于数组元素个数时进行判断。
- 进入循环,首先判断检查右子节点是否存在并且比左子节点的值小,如果是,将
child更新为右子节点的索引,以确保选择更小的子节点进行比较。 - 比较选定的子节点的值与父节点的值,如果子节点的值小于父节点的值,就交换它们。
- 更新parent为新的子节点位置,更新child为新的左子节点位置,然后继续比较和交换,直到不再需要交换为止。
- 如果当前子节点不小于当前父节点则停止循环。
10、获取堆元素个数
int HeapSize(HP* php)
{assert(php);return php->size;
}五、使用堆排序
void HeapSort(int* a, int n)
{HP hp;HeapInit(&hp);// 时间复杂度:N*logNfor (int i = 0; i < n; ++i){HeapPush(&hp, a[i]);}// 时间复杂度:N*logNint i = 0;while (!HeapEmpty(&hp)){int top = HeapTop(&hp);a[i++] = top;HeapPop(&hp);}HeapDestroy(&hp);
}可以使用这种方式,但有诸多弊端:
- 要先有一个堆,太麻烦。
- 空间复杂度+拷贝数据
排降序建小堆
所以我们要在传入的原数组上排降序,需要使用建小堆的方式向上调整。
void HeapSort(int* a, int n)
{// 建堆--向上调整建堆for (int i = 1; i < n; i++){AdjustUp(a, i);}int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);// 再调整,选出次小的数AdjustDown(a, end, 0);--end;}
}
- 从根节点的子节点开始向上建堆,除了根节点以外,每个节点都进行向上调整。
- 定义堆的最后一个节点end为n-1
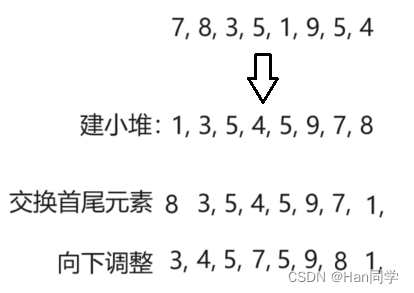
- 我们将堆的根节点(也就是最小值)与堆的最后一个元素交换,即将最小值放到排序尾部即为好的部分。接下来,通过调用
AdjustDown函数,将堆的大小减一,再次将堆调整为最小堆。 - 重复while循环内部操作,直到整个数组排序完成。每次交换和堆的调整都会将最小的元素添加到已排序的部分,直到整个数组都有序。
HeapSort的时间复杂度为O(nlog(n)),它不需要额外的空间来存储数据,所以是一种原地排序算法。它在最坏情况下的性能仍然是O(nlog(n)),因此相对稳定,适用于大规模数据的排序。
我们也可以向下建堆:
倒着调整叶子节点不需要处理,从倒树第一个非叶子节点开始,即最后一个节点的父节点开始调整。
void HeapSort(int* a, int n)
{for (int i = (n - 1 - 1) / 2; i >= 0; --i){ AdjustDown(a, n, i);}int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);// 再调整,选出次小的数AdjustDown(a, end, 0);--end;}
}
完整版:
Heap.h声明部分
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>typedef int HPDataType;
typedef struct Heap
{HPDataType* a;int size;int capacity;
}HP;void HeapInit(HP* php);
void HeapDestroy(HP* php);void AdjustUp(HPDataType* a, int child);
void HeapPush(HP* php, HPDataType x);
bool HeapEmpty(HP* php);
void AdjustDown(int* a, int n, int parent);
void HeapPop(HP* php);HPDataType HeapTop(HP* php);
int HeapSize(HP* php);Heap.c函数部分
#include "Heap.h"void HeapInit(HP* php)
{assert(php);php->a = NULL;php->size = 0;php->capacity = 0;
}void HeapDestroy(HP* php)
{assert(php);free(php->a);php->a = NULL;php->capacity = php->size = 0;
}void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;while (child>0) {if (a[child] < a[parent]) {Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else {break;}}
}void HeapPush(HP* php, HPDataType x)
{assert(php);if (php->size == php->capacity) {int newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* tmp = (HPDataType*)realloc(php->a, newCapacity * sizeof(HPDataType));if (tmp==NULL) {perror("realloc fail");return;}php->a = tmp;php->capacity = newCapacity;}php->a[php->size] = x;php->size++;AdjustUp(php->a, php->size - 1);
}bool HeapEmpty(HP* php)
{assert(php);return php->size==0;
}
void AdjustDown(HPDataType* a, int size, int parent)
{int child = parent * 2 + 1;while (child < size) {if (child + 1 < size && a[child + 1] < a[child]) {child++;}if (a[child] < a[parent]) {Swap(&a[child], &a[parent]);parent = child;child = parent * 2 - 1;}else {break;}}
}void HeapPop(HP* php)
{assert(php);assert(!HeapEmpty(php));Swap(&php->a[0], &php->a[php->size - 1]);php->size--;AdjustDown(php->a, php->size, 0);
}HPDataType HeapTop(HP* php)
{assert(php);assert(!HeapEmpty(php));return php->a[0];
}int HeapSize(HP* php)
{assert(php);return php->size;
}text.c使用及测试部分
#define _CRT_SECURE_NO_WARNINGS 1
#include "Heap.h"void HeapSort(int* a, int n)
{// 建堆--向上调整建堆for (int i = 1; i < n; i++){AdjustUp(a, i);}// 建堆--向下调整建堆//for (int i = (n - 1 - 1) / 2; i >= 0; --i)//{// AdjustDown(a, n, i);//}int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);// 再调整,选出次小的数AdjustDown(a, end, 0);--end;}
}int main()
{int a[] = { 7,8,3,5,1,9,5,4 };HeapSort(a, sizeof(a) / sizeof(int));for (int i = 0; i < 8; i++) {printf("%d ", a[i]);}return 0;
}//---测试堆函数功能---
//int main()
//{
// HP hp;
// HeapInit(&hp);
// int a[] = { 65,100,70,32,50,60 };
// for (int i = 0; i < sizeof(a) / sizeof(int); ++i)
// {
// HeapPush(&hp, a[i]);
// }
//
// while (!HeapEmpty(&hp))
// {
// int top = HeapTop(&hp);
// printf("%d\n", top);
// HeapPop(&hp);
// }
//
// return 0;
//}相关文章:

数据结构与算法:二叉树之“堆排序”
目录 一、树概念及结构 二、二叉树树概念及结构 特殊的二叉树 三、堆的概念及结构 四、堆的创建 1、声明结构体 2、初始化 3、销毁 4、添加新元素 5、交换元素 6、向上调整 7、判断堆是否为空 8、移除堆顶元素 9、向下调整 10、获取堆元素个数 五、使用堆排序…...
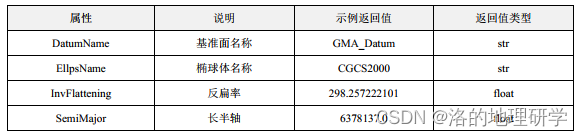
gma 2 教程(三)坐标参考系统:2.基准面/椭球体
安装 gma:pip install gma 地球是一个近似于椭球体的三维物体,而地球上的各种测量和计算都需要一个基准面来进行。基准面是一个虚拟的平面,用于测量和计算地球上的各种物理量。在地球科学中,基准面通常是一个参考椭球体࿰…...

【1day】复现广联达-Linkworks 协同办公管理平台信息泄露漏洞
注:该文章来自作者日常学习笔记,请勿利用文章内的相关技术从事非法测试,如因此产生的一切不良后果与作者无关。 目录 一、漏洞描述 二、影响版本 三、资产测绘 四、漏洞复现...
Spring Cloud之ElasticSearch的学习【详细】
目录 ElasticSearch 正向索引与倒排索引 数据库与elasticsearch概念对比 安装ES、Kibana与分词器 分词器作用 自定义字典 拓展词库 禁用词库 索引库操作 Mapping属性 创建索引库 查询索引库 删除索引库 修改索引库 文档操作 新增文档 查找文档 修改文档 全量…...
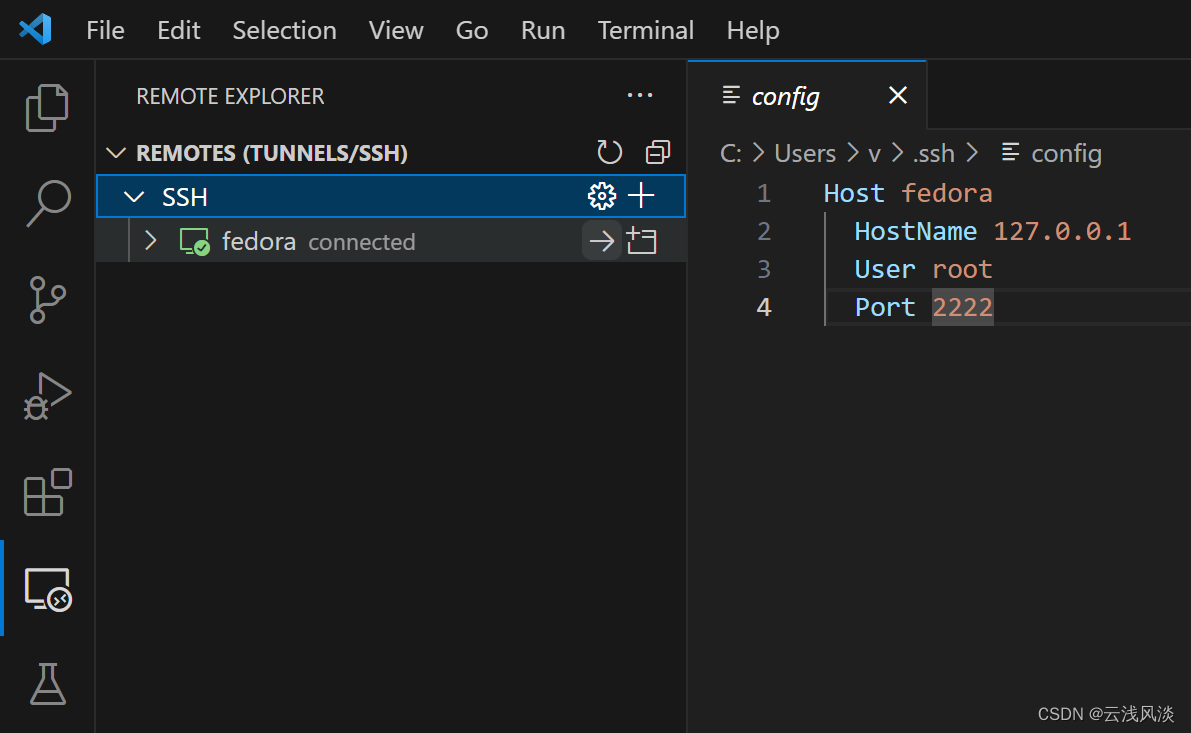
vscode免密码认证ssh连接virtual box虚拟机
文章目录 安装软件virtual box配置vscode配置创建并传递密钥连接虚拟机最后 安装软件 安装vscode和virtual box,直接官网下载对应软件包,下载之后,点击执行,最后傻瓜式下一步安装即可 virtual box配置 创建一个仅主机网络的网卡 …...

【Linux】Centos yum源替换
YUM是基于RPM包管理,能够从指定的服务器自动下载RPM包并且安装,可以自动处理依赖性关系,并且一次安装所有依赖的软件包,无须繁琐地一次次下载、安装。 CentOS 8操作系统版本结束了生命周期(EOL)࿰…...
)
uniapp组件初始化的销毁(监听隐藏事件)
onHide是监听隐藏事件onHide() {console.log("销毁");this.clearTimer(); }, onShow(){console.log("初始化");this.getOrderInfo() },...
leetcode:1207. 独一无二的出现次数(python3解法)
难度:简单 给你一个整数数组 arr,请你帮忙统计数组中每个数的出现次数。 如果每个数的出现次数都是独一无二的,就返回 true;否则返回 false。 示例 1: 输入:arr [1,2,2,1,1,3] 输出:true 解释&…...

2023秋《论文写作》课程总结
2023秋《论文写作》课程总结 授课教师为闵帆教授,原文链接《论文写作》 文章目录 2023秋《论文写作》课程总结一、关于写作工具二、关于写作中的单词、短语、语法等三、关于论文题目四、关于摘要和关键词五、关于引言部分六、关于方法及实验部分七、关于结论八、关…...
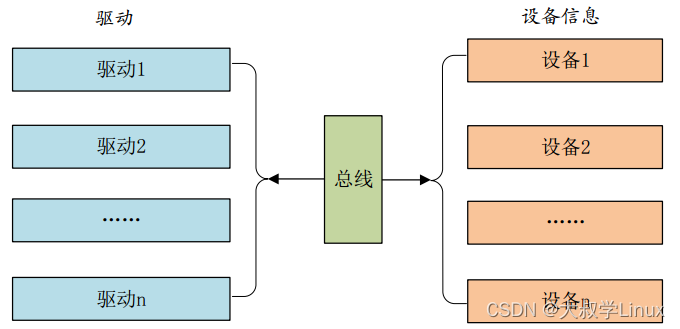
Linux学习第27天:Platform设备驱动开发: 专注与分散
Linux版本号4.1.15 芯片I.MX6ULL 大叔学Linux 品人间百味 思文短情长 专注与分散是我在题目中着重说明的一个内容。这是今天我们要学习分离与分层概念的延伸。专注是说我们要专注某层驱动的开发,而对于其他层则是芯片厂商…...

最长公共子序列
题目描述 给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。 一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符…...
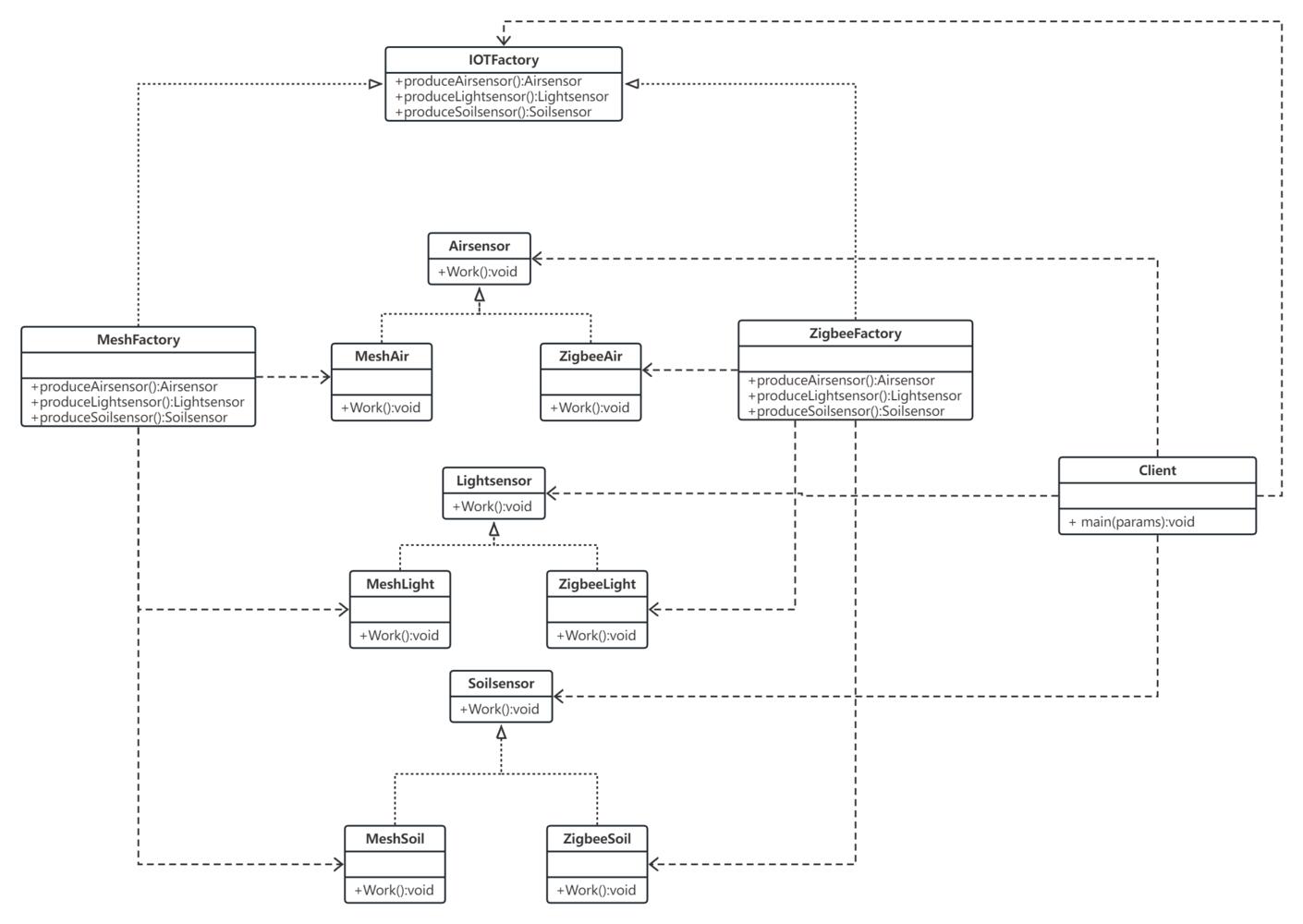
万字解析设计模式之工厂方法模式与简单工厂模式
一、概述 1.1简介 在java中,万物皆对象,这些对象都需要创建,如果创建的时候直接new该对象,就会对该对象耦合严重,假如我们要更换对象,所有new对象的地方都需要修改一遍,这显然违背了软件设计的…...

One-to-N N-to-One: Two Advanced Backdoor Attacks Against Deep Learning Models
One-to-N & N-to-One: Two Advanced Backdoor Attacks Against Deep Learning Models----《一对N和N对一:针对深度学习模型的两种高级后门攻击》 1对N: 通过控制同一后门的不同强度触发多个后门 N对1: 只有当所有N个后门都满足时才会触发…...
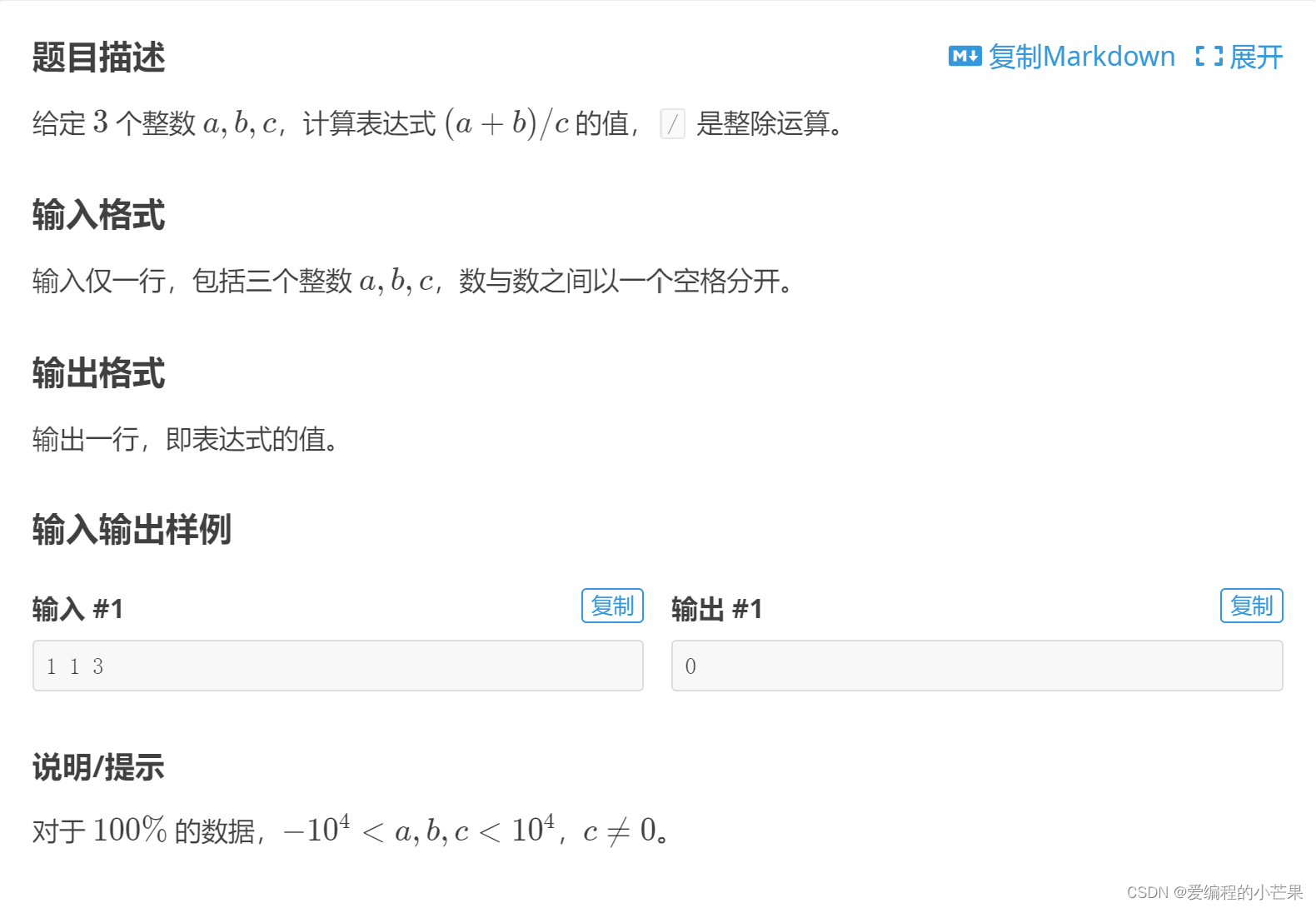
洛谷 B2009 计算 (a+b)/c 的值 C++代码
目录 题目描述 AC Code 切记 题目描述 题目网址:计算 (ab)/c 的值 - 洛谷 AC Code #include<bits/stdc.h> using namespace std; int main() {int a,b,c;cin>>a>>b>>c;cout<<(ab)/c<<endl;return 0; } 切记 不要复制题…...
)
Arduino驱动ME007-ULA防水测距模组(超声波传感器)
目录 1、传感器特性 2、控制器和传感器连线图 3、驱动程序 3.1、读取串口数据...

Linux 权限管理(二)
文件类型和访问权限(事物属性) linux前都会有一串这个字符,第二字符到第九字符分别表示拥有者,所属组,和other所对应的权限。那么第一个字符表示什么呢? 第一个字符表示文件类型: d:…...
线性代数 第一章 行列式
一、概念 不同行不同列元素乘积的代数和(共n!项) 二、性质 经转置行列式的值不变,即; 某行有公因数k,可把k提到行列式外。特别地,某行元素全为0,则行列式的值为0; 两行互换行列式…...

查询Oracle所有用户相关信息
$sqlplus / as sysdba 1. 查询oracle中所有用户信息 select * from dba_users; select * from all_users; select distinct owner from all_objects; 2. 只查询用户和密码 select username,password from dba_users; 3. 查询当前用户信息 select * from dba_ustats; 4…...

电路的电线的拼接
不积跬步无以至千里,今天小编也是复习今天学习的内容,废话不多说,看博客吧!!! 目录 准备条件 操作 成品 准备条件 操作 将定制的套管插入导线当中,24V或者0V是尖端的端子,后面根…...

前端学习之webpack
概述 webpack是一个流行的前端项目构建工具(打包工具),可以解决当前web开发中所面临的问题。 webpack提供了友好的模块化支持,以及代码压缩混淆、处理js兼容问题、性能优化等强大的功能,从而让程序员把工作重心放到具…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...