当前位置： 首页 > news >正文

线性代数 第一章 行列式

news 2025/7/3 10:50:06

一、概念

不同行不同列元素乘积的代数和（共n!项）

二、性质

  1. 经转置行列式的值不变，即\left | A^T \right |=\left | A \right |；

  2. 某行有公因数k，可把k提到行列式外。特别地，某行元素全为0，则行列式的值为0；

  3. 两行互换行列式变号，特别地，两行相等行列式值为0，两行成比例行列式值为0；

  4. 某行所有元素都是两个数的和，则可写成两个行列式之和；

  5. 某行的k倍加至另一行，行列式的值不变。

三、展开式

|A|=ai1Ai1+ai2Ai2＋…+ainAin（按i行展开）

|A|=a1jA1j+a2A2j+…＋anjAnj（按j列展开）

四、计算

4.1 数字型

三角化法、公式法、归纳法

常用技巧

  1. 直接按行（列）展开
  2. 把第1行（列）的k倍加到第i行（列）
  3. 把每行（列）都加到第1行（列）
  4. 逐行（列）相加

4.2 抽象型

  • 用行列式性质
  • 用矩阵性质
  • 用特征值 \left | A \right |=\prod \lambda _i 相似

五、证 \left | A \right |=0

  • Ax=0有非零解

  • 反证法
  • r(A)<n
  • 0是A的特征值
  • \left | A \right |=-\left | A \right |

设某系数行列式为D

D≠0，非齐次线性方程组有唯一解；D=0，可能无穷多解，也可能无解。

D≠0，齐次线性方程组只有零解；D=0，有非零解（即无穷多解）。

六、应用

  • Ax=0有非零解
  • 伴随矩阵求逆法
  • 线性相关（无关）判定
  • 可逆的证明
  • 克拉默法则
  • 特征值计算
  • 二次型正定判定

七、主要公式

  1. 上（下）三角行列式的值等于主对角线元素的乘积
  2. 关于副对角线的行列式=(-1)^{\frac{n(n-1)}{2}}a_{1n}a_{2,n-1}...a_{n1}
  3. 两个特殊的拉普拉斯展开式 主对角线\left | A \right |\cdot \left | B \right | 副对角线(-1)^{mn}\left | A \right |\cdot \left | B \right |
  4. 范德蒙行列式 =\prod_{1\leqslant j< i\leqslant n}(x_i-x_j)
  5. 特征多项式

设A是3阶矩阵，则A的特征多项式\left | \lambda E-A \right |=\lambda ^{3}-(a_{11}+a_{22}+a_{33})\lambda ^{2}+s_2\lambda -\left | A \right |

其中

s_2=\left | \begin{array}{ccc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array}\right | + \left | \begin{array}{ccc} a_{11} & a_{13} \\ a_{31} & a_{33} \end{array}\right | + \left | \begin{array}{ccc} a_{22} & a_{23} \\ a_{32} & a_{33} \end{array}\right |

八、n阶方阵的行列式

\left | A^T \right |=\left | A \right |

\left | kA \right |=k^n \left | A \right |

\left | AB \right |=\left | A \right |\cdot \left | B \right |

\left | A^* \right |=\left | A \right |^{n-1}

\left | A^{-1} \right |=\left | A \right |^{-1}

\left | A \right |=\prod_{i=1}^{n}\lambda _i

if A\sim B,then \left | A \right |=\left | B \right |,\left | A+kE \right |=\left | B+kE \right |

相关文章：

线性代数 第一章 行列式

一、概念 不同行不同列元素乘积的代数和&#xff08;共n!项&#xff09; 二、性质 经转置行列式的值不变&#xff0c;即&#xff1b; 某行有公因数k&#xff0c;可把k提到行列式外。特别地&#xff0c;某行元素全为0&#xff0c;则行列式的值为0&#xff1b; 两行互换行列式…...

编程日记 2023/10/30 22:47:59

查询Oracle所有用户相关信息

$sqlplus / as sysdba 1. 查询oracle中所有用户信息 select * from dba_users; select * from all_users; select distinct owner from all_objects; 2. 只查询用户和密码 select username,password from dba_users; 3. 查询当前用户信息 select * from dba_ustats; 4…...

编程日记 2023/10/30 22:46:57

电路的电线的拼接

不积跬步无以至千里&#xff0c;今天小编也是复习今天学习的内容&#xff0c;废话不多说&#xff0c;看博客吧&#xff01;&#xff01;&#xff01; 目录 准备条件 操作 成品 准备条件 操作 将定制的套管插入导线当中&#xff0c;24V或者0V是尖端的端子&#xff0c;后面根…...

编程日记 2023/10/30 22:44:55

前端学习之webpack

概述 webpack是一个流行的前端项目构建工具&#xff08;打包工具&#xff09;&#xff0c;可以解决当前web开发中所面临的问题。 webpack提供了友好的模块化支持&#xff0c;以及代码压缩混淆、处理js兼容问题、性能优化等强大的功能&#xff0c;从而让程序员把工作重心放到具…...

编程日记 2023/10/30 22:43:54

2023NOIP A层联测20-旅行

小 A 旅行到了远方的一座城市&#xff0c;其内部的道路可以被视为一张包含恰好 n n n 个点以及 n n n 条边的无向连通图。这里的居民可以用一种特质的墨水来改变图中某一条边的颜色。 居民们的狂欢节即将开始了&#xff0c;且节日会持续 m m m 天。每一天&#xff0c;居民们…...

编程日记 2023/10/30 22:42:53

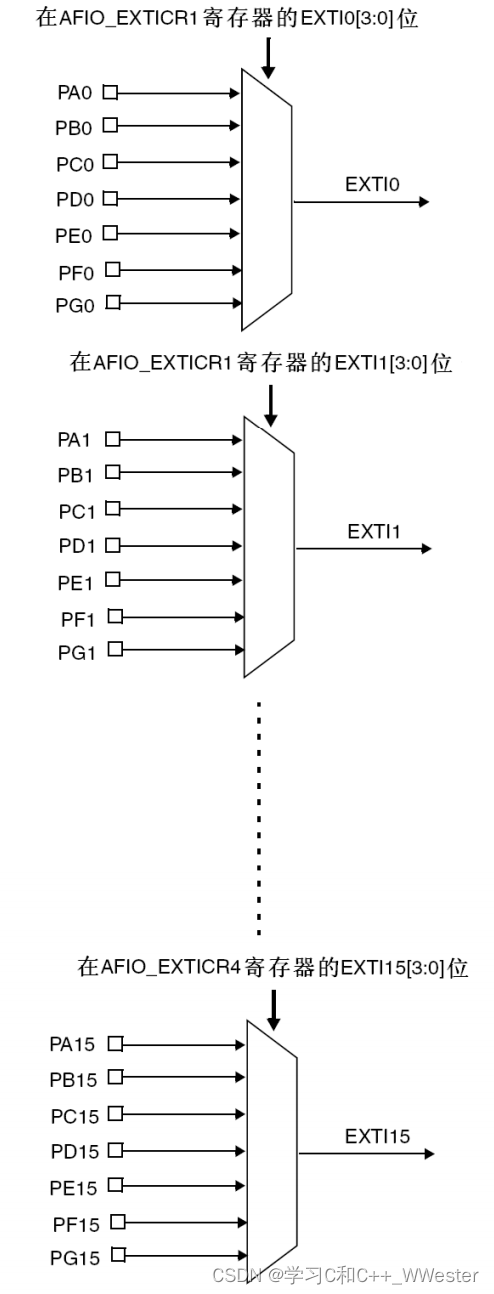
STM32 中断NVIC详解，配置及示例

NVIC全称 Nested Vectored Controller 嵌套向量中断控制器 它是一种硬件设备&#xff0c;用于管理和协调处理器的中断请求。NVIC可以管理多个中断请求&#xff0c;并按优先级处理它们。当一个中断请求到达时&#xff0c;NVIC会确定其优先级并决定是否应该中断当前执行的程序&am…...

编程日记 2023/10/30 22:41:52

10.30英语期中稿

influence of Chinese and Japanese literary culture on the country and the world, and compare the differences between the two 对自己文化影响 中日文学文化比较 表达&#xff0c;餐饮&#xff0c;服装 相似点与不同点 与日本友人交流 draft Chinese and Japanes…...

编程日记 2023/10/30 22:39:51

二维数组如何更快地遍历

二维数组如何更快地遍历 有时候&#xff0c;我们会发现&#xff0c;自己的代码和别人的代码几乎一模一样&#xff0c;但运行时间差了很多&#xff0c;别人是 AC \text{AC} AC&#xff0c;你是 TLE \text{TLE} TLE&#xff0c;这是为什么呢&#xff1f; 一个可能的原因是数组的…...

编程日记 2023/10/30 22:35:48

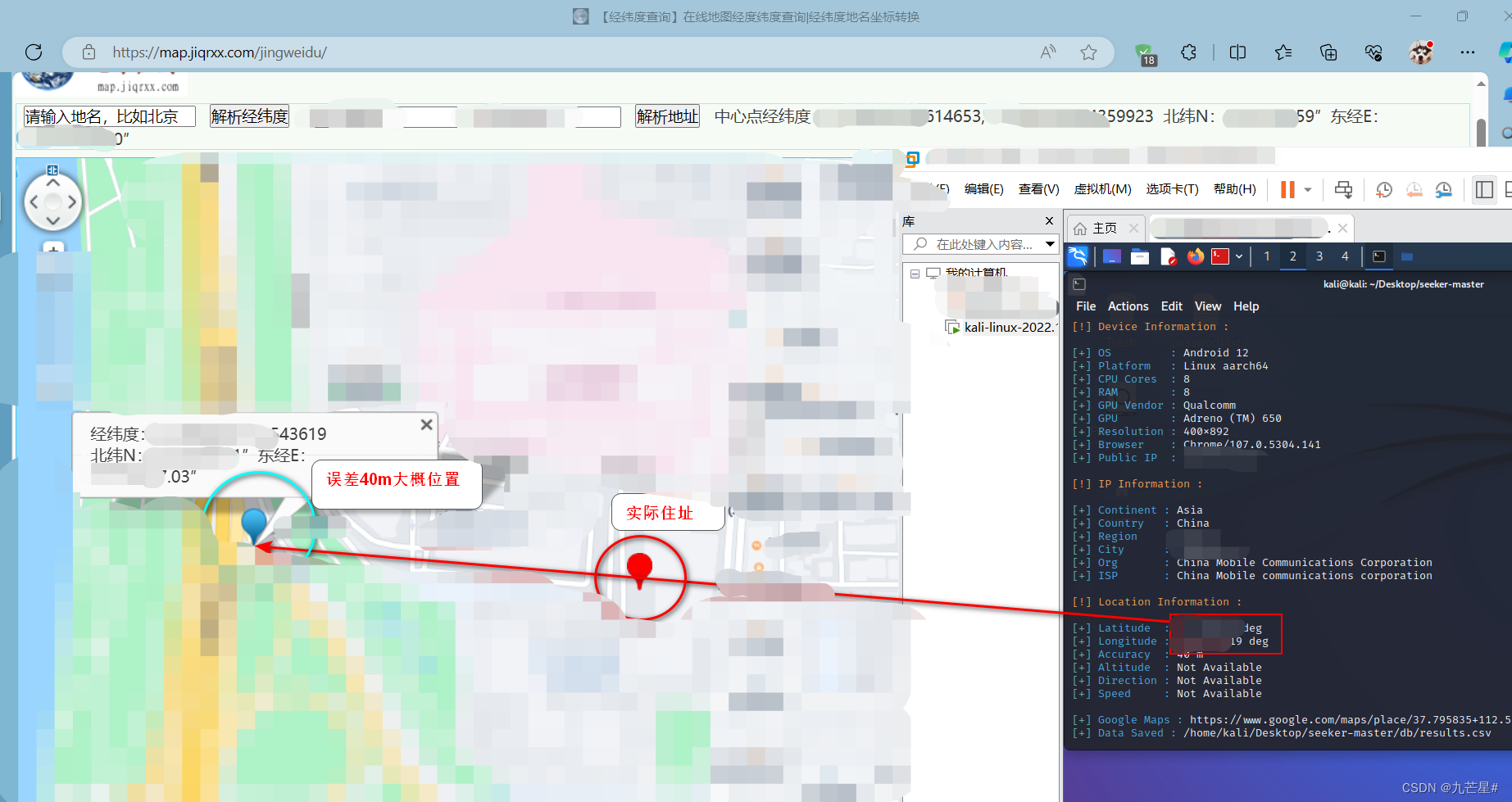
【网络安全】Seeker内网穿透追踪定位

Seeker追踪定位对方精确位置 前言一、kali安装二、seeker定位1、ngrok平台注册2、获取一次性邮箱地址3、ngrok平台登录4、ngrok下载5、ngrok令牌授权6、seeker下载7、运行seeker定位8、运行隧道开启监听9、伪装链接10、用户点击&#xff08;获取定位成功&#xff09;11、利用经…...

编程日记 2023/10/30 22:34:47

Spring Boot 3系列之一（初始化项目）

近期&#xff0c;JDK 21正式发布&#xff0c;而Spring Boot 3也推出已有一段时间。作为这两大技术领域的新一代标杆&#xff0c;它们带来了许多令人振奋的新功能和改进。尽管已有不少博客和文章对此进行了介绍&#xff0c;但对于我们这些身处一线的开发人员来说&#xff0c;有些…...

编程日记 2023/10/30 22:33:46

用python判断一个数是否为素数

判断一个数是否为素数可以使用以下方法&#xff1a; 排除特殊情况&#xff1a;首先判断该数是否小于等于1&#xff0c;因为素数定义中&#xff0c;素数必须大于1。如果小于等于1&#xff0c;则该数不是素数。 除尽法&#xff08;试除法&#xff09;&#xff1a;从2开始&#x…...

编程日记 2023/10/30 22:32:44

FreeRTOS_信号量之二值信号量

目录 1. 信号量简介 2. 二值信号量 2.1 二值信号量简介 2.1.1 二值信号量无效 2.1.2 中断释放信号量 2.1.3 任务获取信号量成功 2.1.4 任务再次进入阻塞态 2.2 创建二值信号量 2.2.1 vSemaphoreCreateBinary() 2.2.2 xSemaphoreCreateBinary() 2.2.3 xSemaphoreCrea…...

编程日记 2023/10/30 22:31:44

使用Gateway解决跨域问题时配置文件不生效的情况之一

首先html文件只有一个发送ajax请求 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" content"IEedge"><meta name"viewport" content&q…...

编程日记 2023/10/30 22:30:42

【火影手游】新版押镖护送高分攻略

文章目录 Part.I IntroductionPart.II 迪达拉视角1、打栅栏2、石头边&#xff0c;打石头和栅栏3、石头边&#xff0c;踩封印&#xff0c;撞力士4、大树前&#xff0c;打石头和栅栏5、石头边&#xff0c;给佩恩当路标6、后一前二接大招7、补伤害 Part.III 佩恩视角1、头进洞&…...

编程日记 2023/10/30 22:28:40

【JVM】类的声明周期（加载、连接、初始化）

&#x1f40c;个人主页&#xff1a; &#x1f40c; 叶落闲庭 &#x1f4a8;我的专栏&#xff1a;&#x1f4a8; c语言 数据结构 javaEE 操作系统 Redis 石可破也&#xff0c;而不可夺坚&#xff1b;丹可磨也&#xff0c;而不可夺赤。 JVM 一、类的声明周期&#xff08;加载阶段…...

编程日记 2023/10/30 22:27:39

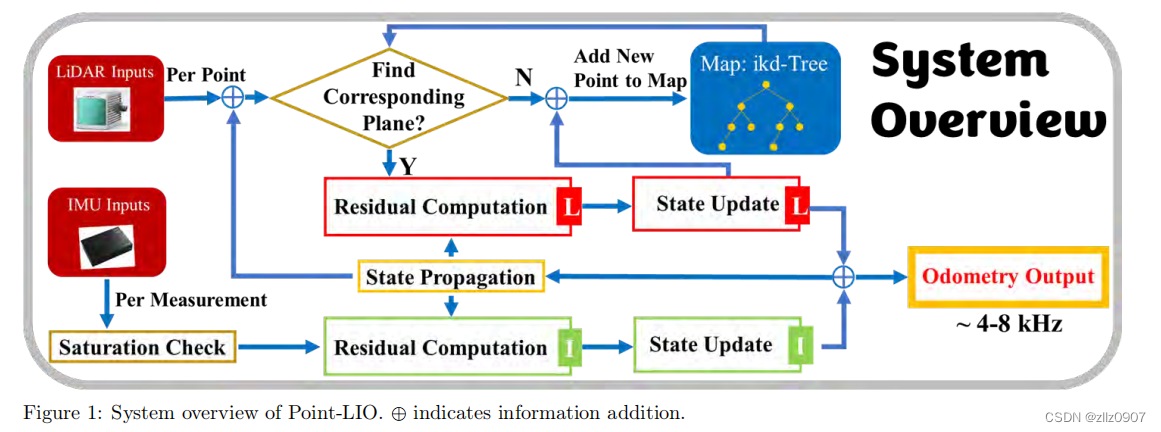
开源3D激光（视觉）SLAM算法汇总（持续更新）

原文连接 目录 一、Cartographer 二、hdl_graph_slam 三、LOAM 四、LeGO-LOAM 五、LIO-SAM 六、S-LOAM 七、M-LOAM 八、livox-loam 九、Livox-Mapping 十、LIO-Livox 十一、FAST-LIO2 十二、LVI-SAM 十三、FAST-Livo 十四、R3LIVE 十五、ImMesh 十六、Point-LIO 一、Cartograph…...

编程日记 2023/10/30 22:26:37

绕WAF手法总结

云锁 被拦截 http://www.test123.com/article.php?id1%20union%20select%201,2,3 绕过 http://www.test123.com/article.php?id-1/*!36000union*//*!36000distinct*//*!36000select*/1,2,user() 360websec 被拦截 http://www.xxx.com.cn/productshow.php?id79 绕过 http:/…...

编程日记 2023/10/30 22:25:36

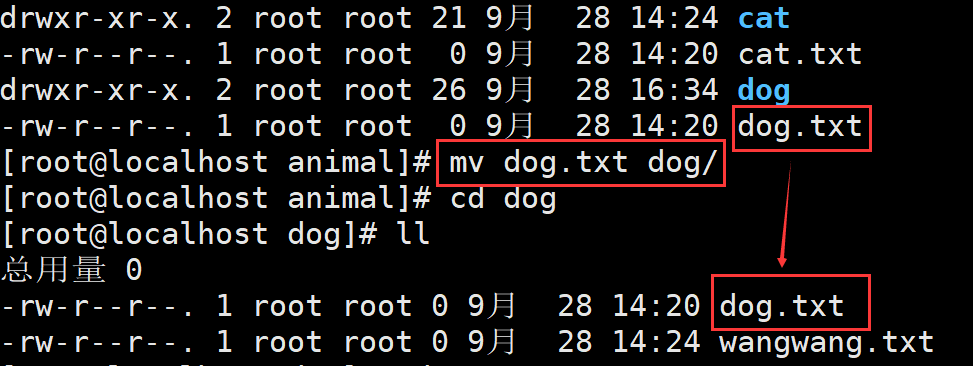
Linux mv命令：移动文件或改名

mv 命令&#xff08;move 的缩写&#xff09;&#xff0c;既可以在不同的目录之间移动文件或目录&#xff0c;也可以对文件和目录进行重命名。该命令的基本格式如下&#xff1a; [rootlocalhost ~]# mv 【选项】 源文件 目标文件 -f&#xff1a;强制覆盖&#xff0c;如果目标文…...

编程日记 2023/10/30 22:24:35

在 Elasticsearch 中丰富你的 Elasticsearch 文档

作者&#xff1a;David Pilato 对于 Elasticsearch&#xff0c;我们知道联接应该在 “索引时” 而不是查询时完成。 本博文是一系列三篇博文的开始&#xff0c;因为我们可以在 Elastic 生态系统中采取多种方法。 我们将介绍如何在 Elasticsearch 中做到这一点。 下一篇博文将介…...

编程日记 2023/10/30 22:23:33

探营云栖大会：蚂蚁集团展出数字人全栈技术，三大AI“机器人”引关注

一年一度的科技盛会云栖大会将于10月31日正式开幕。30日&#xff0c;记者来到云栖大会展区探营&#xff0c;提前打卡今年上新的“黑科技”。 记者在蚂蚁集团展馆看到&#xff0c;超1亿人参与的亚运“数字火炬手”全栈技术首次公开展示&#xff0c;还可体验基于数字人技术的“数…...

编程日记 2023/10/30 22:21:31

Flask RESTful 示例

目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题&#xff1a; 下面创建一个简单的Flask RESTful API示例。首先&#xff0c;我们需要创建环境&#xff0c;安装必要的依赖&#xff0c;然后…...

编程新知 2025/6/30 10:44:58

相机从app启动流程

一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下： 重点代码分析： 启动相机前，先要通过getCameraIdList获取camera的个数以及id，然后可以通过getCameraCharacteristics获取对应id camera的capabilities（静态信息）进行一些openCamera前的…...

编程新知 2025/6/19 2:36:50

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测；从基础到高级，涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等

&#x1f50d; 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术&#xff0c;可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势&#xff0c;还能有效评价重大生态工程…...

编程新知 2025/6/21 14:45:36

大模型多显卡多服务器并行计算方法与实践指南

一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术，以解决单机资源不足的问题。分布式训练主要分为两种模式： 数据并行：将数据分片到不同设备，每个设备拥有完整的模型副本 模型并行：将模型分割到不同设备，每个设备处理部分模型计算 现代大模型训练通常结合…...

编程新知 2025/6/24 6:21:26

拉力测试cuda pytorch 把 4070显卡拉满

import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试&#xff0c;通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小&#xff0c;增大可提高计算复杂度duration: 测试持续时间&#xff08;秒&…...

编程新知 2025/6/21 10:39:11

GC1808高性能24位立体声音频ADC芯片解析

1. 芯片概述 GC1808是一款24位立体声音频模数转换器&#xff08;ADC&#xff09;&#xff0c;支持8kHz~96kHz采样率&#xff0c;集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器&#xff0c;适用于高保真音频采集场景。 2. 核心特性 高精度&#xff1a;24位分辨率&#xff0c…...

编程新知 2025/7/3 3:02:27

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的？

uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件&#xff0c;用于在原生应用中加载 HTML 页面&#xff1a; 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

编程新知 2025/6/21 2:45:17

Android第十三次面试总结（四大 组件基础）

Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成&#xff0c;用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机&#xff1a; ​onCreate()​​ ​调用时机​&#xff1a;Activity 首次创建时调用。​…...

编程新知 2025/6/21 16:37:38

【Java学习笔记】BigInteger 和 BigDecimal 类

BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点&#xff1a;传参类型必须是类对象 一、BigInteger 1. 作用&#xff1a;适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

编程新知 2025/6/21 16:56:20

VM虚拟机网络配置（ubuntu24桥接模式）：配置静态IP

编辑-虚拟网络编辑器-更改设置 选择桥接模式&#xff0c;然后找到相应的网卡&#xff08;可以查看自己本机的网络连接&#xff09; windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置&#xff0c;选择刚才配置的桥接模式 静态ip设置&#xff1a; 我用的ubuntu24桌…...

编程新知 2025/6/26 5:18:35