论文范文:论基于架构的软件设计方法及应用

注意:范文只适用于帮助大家打开写作思路,并不能作为素材直接用于平时练习、考试中。考试中直接使用范文的素材,会有被认定为雷同卷的风险。
摘要:
2022年4月,本人所在单位计划研发生态集装箱管理控制平台项目。该平台主要用于与现有公司生态集装箱产品做对接,达到远程控制、平台管理,为集装箱生态种植提质提效的目的。本人在项目中担任架构师,负责系统的架构设计。本文以生态集装箱管理平台项目为例,主要论述基于架构的软件设计方法在该项目中的应用。在架构需求阶段,我们采用了用例图、类图等进行用例模型和分析模型的建立,完成需求分析问题。在架构设计阶段,我们采用了面向对象的软件设计方法,解决了系统架构设计问题。在架构复审阶段,我们采用了架构权衡分析方法(简称ATAM),完成了架构的质量和功能评估,评审架构可能存在的风险以及缺陷。经过合理有效地运用基于架构的软件设计方法,本项目得以成功上线,并获得客户的一致好评。
正文:
2022年4月,本人所在的单位按照既定的企业系统战略规划,同时经过市场调研与分析,决定研发生态集装箱管理控制平台。生态集装箱为无尘的水培作物环境,以本地嵌入式系统为核心调各种环境参数。在产品的使用中,生态集装箱的本地操作与控制,状态检测等工作对使用者极为个便,对其进行物联网化改造成了急需解决的需求问题。生态集装箱管理控制平台项目主要完成集装箱的远程监控、远程操作、协作管理等,在方便用户使用,提高集装箱产物的产量与品
相关文章:

论文范文:论基于架构的软件设计方法及应用
注意:范文只适用于帮助大家打开写作思路,并不能作为素材直接用于平时练习、考试中。考试中直接使用范文的素材,会有被认定为雷同卷的风险。 摘要: 2022年4月,本人所在单位计划研发生态集装箱管理控制平台项目。该平台主要用于与现有公司生态集装箱产品做对接,达到远程控制…...
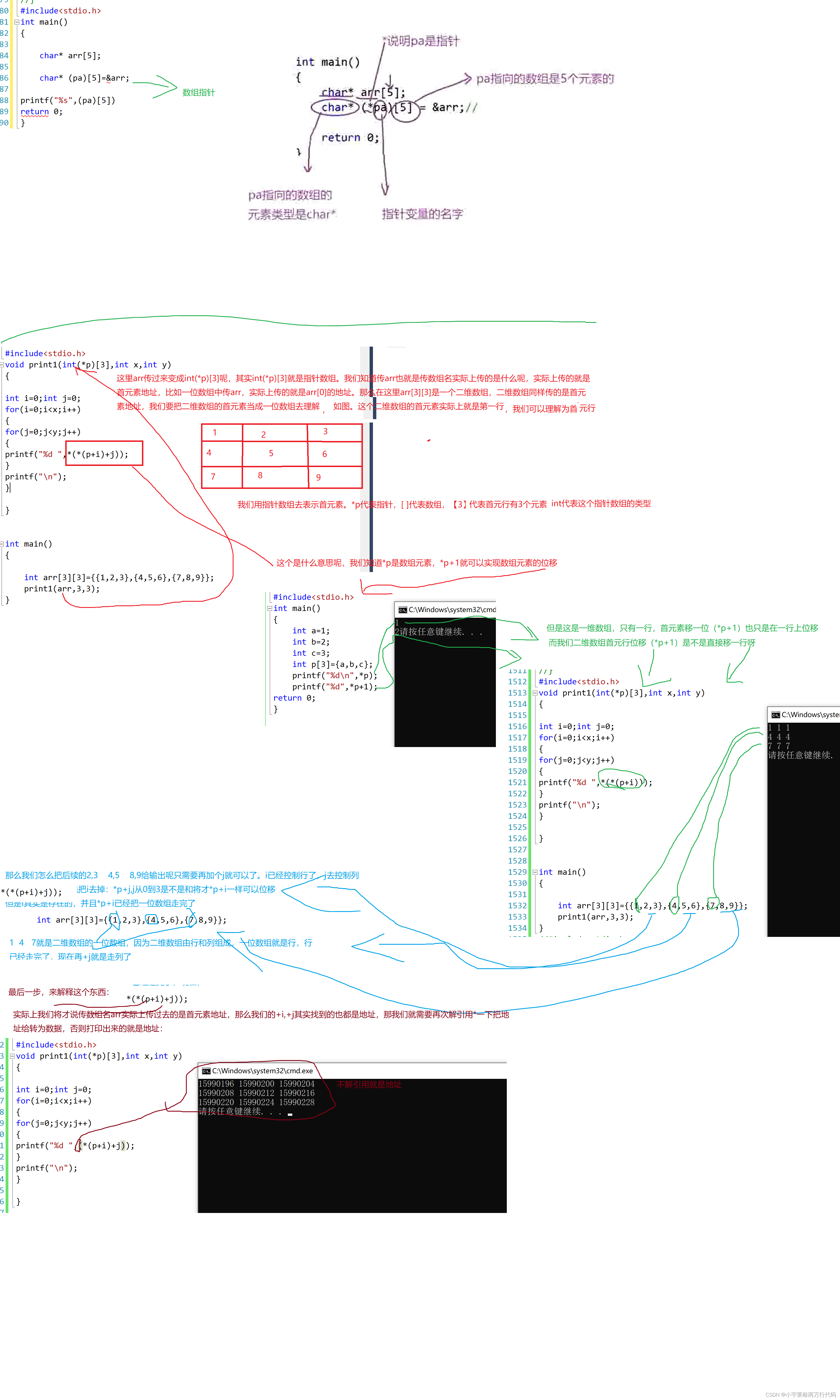
C语言 指针进阶笔记
p和*p: 如图,p是指针,指针存放着地址,打印出来应该是数组的值 *p是指针里里面的元素 #include<stdio.h> int main() {int a1;int b2;int c3;int p[3]{a,b,c};printf("%d",*p); return 0; } 那么现在的打印结果应该为数组的…...

数据库认证 | Oracle OCP好考吗
数据库对于很多技术人员来说都不陌生,但是你想深入了解的话,那么考个证书也许就是一个不错的选择。 如果能考个Oracle OCP认证的话,那也确实不错。那么Oracle OCP好考吗?下面我们就来了解一下吧。 01 Oracle OCP好考吗 OCP考试还…...

处理大数据的基础架构,OLTP和OLAP的区别,数据库与Hadoop、Spark、Hive和Flink大数据技术
处理大数据的基础架构,OLTP和OLAP的区别,数据库与Hadoop、Spark、Hive和Flink大数据技术 2022找工作是学历、能力和运气的超强结合体,遇到寒冬,大厂不招人,可能很多算法学生都得去找开发,测开 测开的话&am…...
解决计算机msvcp120.dll文件丢失的5种方法,亲测有效
在计算机使用过程中,我们经常会遇到一些错误提示,其中之一就是“msvcp120.dll丢失”。这个错误提示可能会给我们带来很大的困扰,影响我们的正常使用。本文将详细介绍msvcp120.dll丢失的原因、解决方法以及预防措施,帮助大家更好地…...

Python selenium交互
视频版教程:一天掌握python爬虫【基础篇】 涵盖 requests、beautifulsoup、selenium selenium可以模拟用户点击事件,以及控制浏览器前进,后退等操作。 下面是一个模拟百度搜索,点击下一页,控制浏览器后退,…...

基本微信小程序的体检预约小程序
项目介绍 我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,体检预约系统小程序被用户普遍使用,为方便用户…...

FHE 的高精度算术:BGV-big、BFV-big
参考文献: [NL11] Naehrig M, Lauter K, Vaikuntanathan V. Can homomorphic encryption be practical?[C]//Proceedings of the 3rd ACM workshop on Cloud computing security workshop. 2011: 113-124.[GC15] Geihs M, Cabarcas D. Efficient integer encoding…...
基于SpringBoot的在线笔记系统
技术介绍 🔥采用技术:SpringSpringMVCMyBatisJSPMaven 🔥开发语言:Java 🔥JDK版本:JDK1.8 🔥服务器:tomcat 🔥数据库:mysql 🔥数据库开发工具&…...
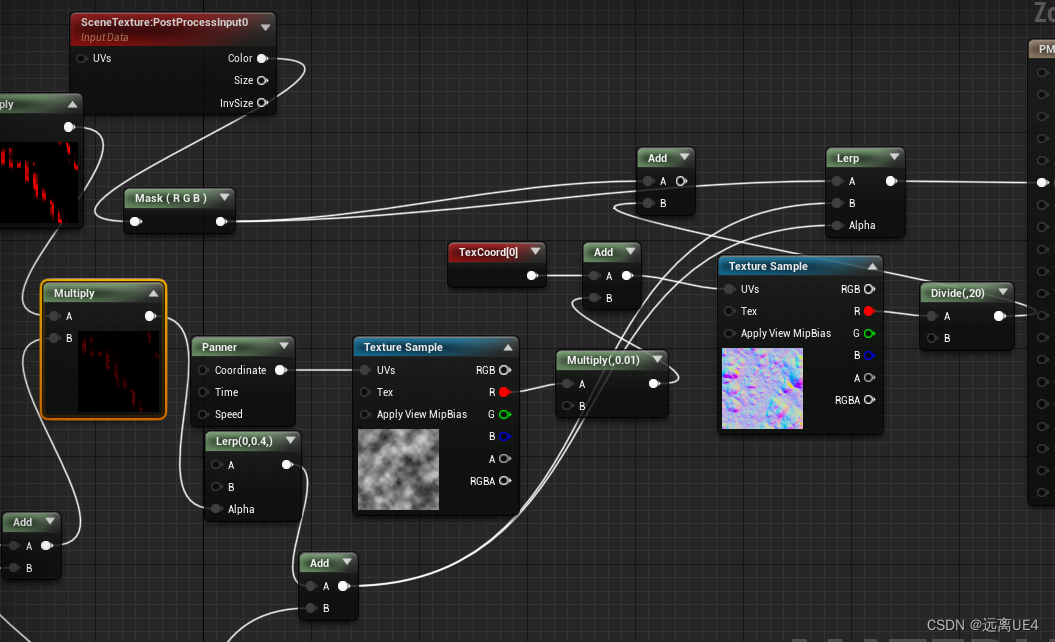
UE4 使用材质后期 制作玻璃有雨效果
效果展示,其实这是一个动画效果 以上为所有逻辑 拿到TexCoord给到Panner,Time和Speed都是通过下面计算而来,后面讲,再拿到时间和速度值过后,加上扰动值,最后取G值,因为雨事从上而下的动…...
:笔记检验概述)
笔记检验(一):笔记检验概述
文章目录 一、 笔迹的概念及成分(一) 笔迹的概念(二) 笔迹的成分 二、 笔迹检验的概念、任务及作用(一) 笔迹检验的概念(二) 笔迹检验的任务(三) 笔记检验的作…...

NOIP2023模拟6联测27 C. 点餐
NOIP2023模拟6联测27 C. 点餐 题目大意 有 n n n 种菜品,每样菜品有 a i , b i a_i , b_i ai,bi 假设有某位顾客点了 k k k 样菜品,那么价格为 ∑ i 1 k a p i max i 1 k b p i \sum_{i 1}^k a_{p_i}\max_{i 1}^kb_{p_i} ∑i1kapi…...

简单聊聊远程协同运维定义以及优势-行云管家
很多新人小伙伴对于远程协同运维不是很了解,今天我们就来简单聊聊远程协同运维定义以及优势。 远程协同运维定义 远程协同运维其实非常容易理解,主要是指计算机系统技术服务工程相关的人员通过局域网或者是其他网络对于它来进行连接,共同远…...

Ortec974A EPICS IOC程序
Ortec974A设备介绍,请见Ortec -- 974A 四通道100-MHz计时器/计数器_ortec974a_EPICS Technical的博客-CSDN博客 1) 创建一个用户存放这个IOC程序结构的目录: rootorangepi4-lts:/usr/local/EPICS/program# mkdir ortec974A rootorangepi4-l…...

JS-文件下载,实现在ios也是下载 而不是预览,
需求 通过A链接的方式,把从后台获取到的文件下载到本地,实现在移动端,PC端都能下载 问题 通过ajax请求后端生成的文件流之后,创建BLOB文件进行下载,在PC端和移动安卓端都可以实现下载到本地和对应的手机,而在IOS端的…...

Leetcode.275 H 指数 II
题目链接 Leetcode.275 H 指数 II mid 题目描述 给你一个整数数组 c i t a t i o n s citations citations ,其中 c i t a t i o n s [ i ] citations[i] citations[i] 表示研究者的第 i i i 篇论文被引用的次数, c i t a t i o n s citations citat…...

代码随想录Day40-单调栈:力扣第496e、503m、42h、84h题
496e. 下一个更大元素 I 题目链接 代码随想录文章讲解链接 方法一:单调栈哈希表 用时:13m52s 思路 维护一个栈底到栈顶是单调递减的栈,从后往前遍历数组nums2,更新栈。nums2当前元素nums2[i]的下一个更大元素就是栈顶元素&am…...
Git窗口打开vim后如何退出编辑(IDEA/Goland等编辑器)
最近在学习git高级操作过程中,遇到了一下问题: 我在学习Git合并多个commit为一个的时候,需要输入一个命令 git rebase -i HEAD~2 这说明已经是编辑模式了。当我写好后,我还按照原来在linux上的按下ESC键,但是只是光…...

【CSDN 每日一练 ★★☆】【二叉树/BSF】二叉树的层序遍历
【CSDN 每日一练 ★★☆】【二叉树/BSF】二叉树的层序遍历 二叉树 BSF 题目 给你一个二叉树,请你返回其按 层序遍历 得到的节点值。 (即逐层地,从左到右访问所有节点)。 示例: 二叉树:[3,9,20,null,nul…...
Golang | Zinx学习笔记(一)
参考 http://zinx.me/ https://www.kancloud.cn/aceld/zinx/1960213 https://www.yuque.com/aceld/tsgooa/gx01meg5ow4pftac 说明 zinx是一个基于Golang的轻量级并发服务器框架。 目前zinx已经在很多企业进行开发使用,具体使用领域包括:后端模块的消息中转、长链…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...
