记录一段帮朋友写的代码,使用牛顿-拉夫逊方法解方程
要求
已知公式:
t = G + A B F r + B r 2 2 F + A 2 B + G A F ln ( r − A ) + C o n s t t=\frac{G+AB}{F}r+\frac{Br^2}{2F}+\frac{A^2B+GA}{F}\ln (r-A)+Const t=FG+ABr+2FBr2+FA2B+GAln(r−A)+Const
其中
- t 的值为0-1000,每间隔25取一次值
- A=2.12941E-10
- B=0.637224706
- F=1.2652E-08
- G=4.28646E-06
- Const=1.90196E-06
求r的值。
解法
要解这样的方程通常需要用到数值方法。对于这样的复杂方程,我们可以使用牛顿-拉夫逊法来求解。
牛顿-拉夫逊方法的基本思想是:从一个初始猜测值开始,使用函数的导数(或切线的斜率)来更新猜测值,逐步逼近函数的真实零点。
首先,我们需要定义方程和它的导数,然后根据初始值逐渐逼近正确的解。
/*使用牛顿-拉夫逊法来求解。
牛顿-拉夫逊方法的基本思想是:从一个初始猜测值开始,使用函数的导数(或切线的斜率)来更新猜测值,逐步逼近函数的真实零点。
首先,定义方程function和它的导数定义了方程和其导数derivative,然后根据初始值逐渐逼近正确的解。
newtonRaphson函数使用牛顿-拉夫逊方法迭代地逼近方程的根,从一个初始猜测值开始。
*/
#include <stdio.h>
#include <math.h>
// 设置阈值,用于决定函数的值何时足够接近于0
// 当函数的值的绝对值小于这个阈值时,可以认为我们找到了方程的一个解
#define TOLERANCE 1e-6
// 设置去迭代的最大次数,防止无限迭代
#define MAX_ITER 1000double A = 2.12941E-10;
double B = 0.637224706;
double F = 1.2652E-08;
double G = 4.28646E-06;
double Const = 1.90196E-06;// 定义函数
double function(double r, double t) {return (G + A * B) * r / F + B * r * r / (2 * F) + (A * A * B + G * A) * log(r - A) / F + Const - t;
}// 定义函数对r的导数
double derivative(double r) {return (G + A * B) / F + B * r / F + (A * A * B + G * A) / (F * (r - A));
}// 使用牛顿-拉夫逊法求解
double newtonRaphson(double t) {double r = 1.0; // 初始的猜测值for (int i = 0; i < MAX_ITER; i++) {double f = function(r, t); // 函数在当前猜测值处的值double f_prime = derivative(r); // 函数在当前猜测值处的导数值(也就是切线的斜率)// f的绝对值小于阈值,返回r值if (fabs(f) < TOLERANCE)return r;r = r - f / f_prime; // 牛顿-拉夫逊方法中的关键更新步骤,用于寻找函数的零点或根}// 超过迭代的最大次数,返回r值return r;
}int main() {int i=1;for (double t = 25; t <= 1000; t += 25) {printf("第%d次迭代:",i++);double r = newtonRaphson(t);printf("t = %lf, r = %lf\n", t, r);}return 0;
}运行结果:

这里,我随机选择了r = 1.0作为开始迭代的初始值。选择合适的初始猜测值很重要,因为不同的初始值可能会导致不同的收敛结果,或者在某些情况下可能不会收敛。如果r = 1.0不适用于这个方程或特定的t值范围,可能需要根据实际情况调整这个值。
通常,基于对问题的了解和对方程的形状有一定的认识,选择一个合理的初始值是有帮助的。如果不确定最佳的初始猜测值是多少,可以尝试多个值并检查结果的稳定性。
另外,阈值TOLERANCE和最大迭代次数MAX_ITER的值也需要自行根据经验选择。
相关文章:

记录一段帮朋友写的代码,使用牛顿-拉夫逊方法解方程
要求 已知公式: t G A B F r B r 2 2 F A 2 B G A F ln ( r − A ) C o n s t t\frac{GAB}{F}r\frac{Br^2}{2F}\frac{A^2BGA}{F}\ln (r-A)Const tFGABr2FBr2FA2BGAln(r−A)Const 其中 t 的值为0-1000,每间隔25取一次值A2.12941E-10B0.…...

滑动窗口限流算法实现一
固定算法 原理:固定算法是将时间线分隔成固定大小的时间窗口,每个窗口都会有个计数器,用来记录窗口时间范围内的请求总数,如果窗口的请求总数达到最大限定值,会认定流量超限。比如将窗口大小设为1分钟,每分…...

简单明了!网关Gateway路由配置filters实现路径重写及对应正则表达式的解析
问题背景: 前端需要发送一个这样的请求,但出现404 首先解析请求的变化: http://www.51xuecheng.cn/api/checkcode/pic 1.请求先打在nginx,www.51xuecheng.cn/api/checkcode/pic部分匹配到了之后会转发给网关进行处理变成localho…...

EMQX内置Web管理控制台-Dashboard
一、Dashboard概述 EMQX Dashboard官网文档:https://docs.emqx.com/zh/enterprise/v5.1/dashboard/introduction.html 1、简介 EMQX 为用户提供了一个功能强大的内置管理控制台,即 EMQX Dashboard。通过这个控制台的 Web 界面,用户可以轻松监…...
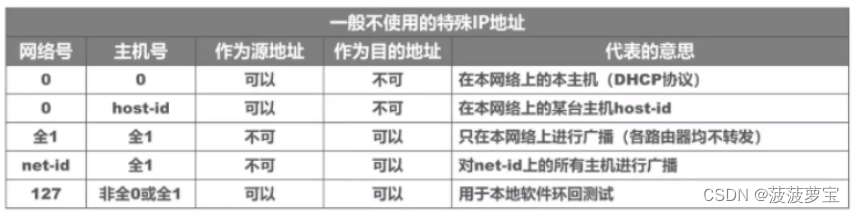
计算机网络重点概念整理-第四章 网络层【期末复习|考研复习】
计算机网络复习系列文章传送门: 第一章 计算机网络概述 第二章 物理层 第三章 数据链路层 第四章 网络层 第五章 传输层 第六章 应用层 第七章 网络安全 计算机网络整理-简称&缩写 文章目录 前言四、网络层4.1 网络层功能4.1.1 电路交换、报文交换与分组交换4.1…...

数组转树形数据
const nodes [{ id: 3, name: 节点C, pid: 1 },{ id: 6, name: 节点F, pid: 3 },{ id: 0, name: root, pid: null },{ id: 1, name: 节点A, pid: 0 },{ id: 8, name: 节点H, pid: 4 },{ id: 4, name: 节点D, pid: 1 },{ id: 2, name: 节点B, pid: 0 },{ id: 5, name: 节点E, p…...

react动态插入样式
在开发组件过程中,偶尔需要动态的插入css,比如在在iframe中渲染组件后,iframe中是没有样式的,所以需要手动插入样式。 插入样式 通常是在useLayoutEffect中动态创建style标签 useLayoutEffect(() > {if (!ref.current) {cons…...
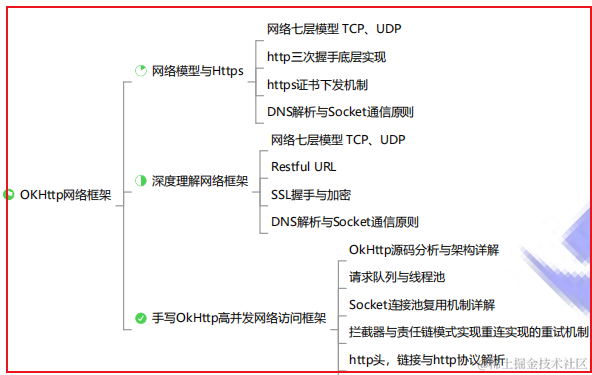
OkHttp网络框架深入理解-SSL握手与加密
OkHttp简介 由Square公司贡献的一个处理网络请求的开源项目,是目前Android使用最广泛的网络框架。从Android4.4开始HttpURLConnection的底层实现采用的是OkHttp。 特点: 支持HTTP/2并允许对同一主机的所有请求共享一个套接字通过连接池,减少了请求延迟…...
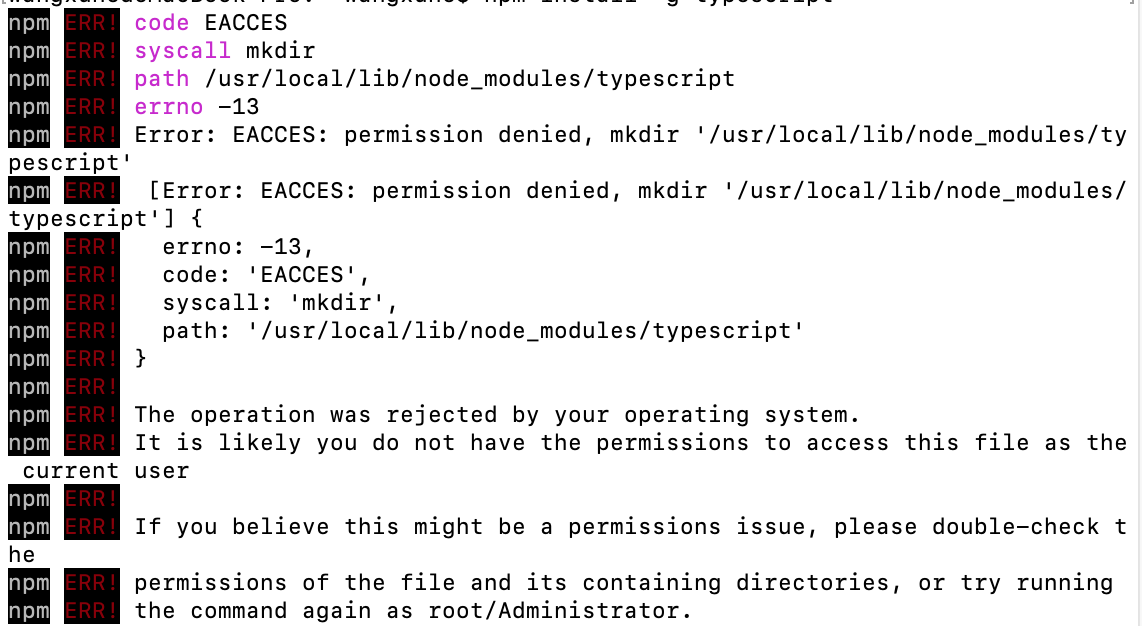
Mac 安装使用NPM及常用命令
环境: Mac 工具: NPM 可通过官网查询一些模块相关 NPM Doc 通过官网文档了解更多的关于NPM的使用 安装 NPM是Node.js的包管理工具,可用于解决 Node.js在代码部署上的问题。 新版本的Node.js已经集成了NPM, 因此可通过下载 Nod…...

利用 JSqlParser 防止 SQL 注入
高手文章《jsqlparser:实现基于SQL语法分析的SQL注入攻击检查》介绍了利用 JSqlParser 防止 SQL 注入,写得很好,只不过有两个问题,代码比较复杂,我于是作了简化,只有两个类;其次检测比较严格,连…...

10.27~10.29数电第三次实验分析与问题
实验要求 分析 寄存器 D触发器有两个输出口,一个输入口,一个时钟信号,一个复位信号 同步异步就是说复位信号在不在always里 给它加一个load就成了一位寄存器, 寄存器堆 8个8位的寄存器堆,每个寄存器都有两读一写…...
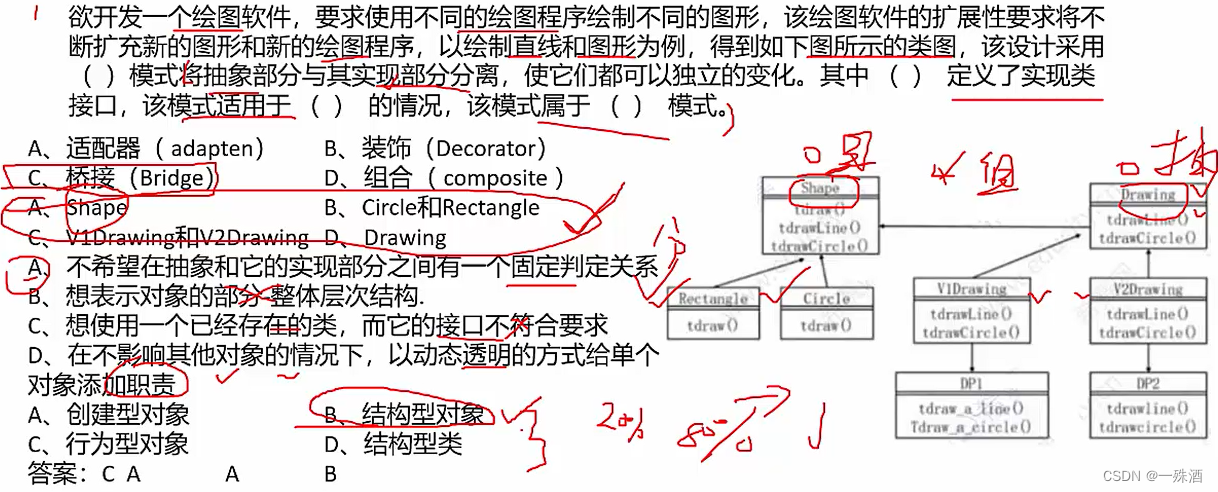
【软考】14.3 设计模式
《设计模式》 有下划线:类模式 / 对象模式无下划线:对象模式 创建型 设计模式 创建对象 构建器(Builder):类和构造分离抽象工厂(Abstract Factory):抽象接口工厂(Factor…...

Mac docker+vscode
mac 使用docker vs code 通过vscode 可以使用docker容器的环境。 可以在容器安装gdb, 直接调试代码。 创建容易时候可以指定目录和容易目录可以共享文件。...
)
LLVM学习笔记(58)
4.4. 目标机器对象 在main()函数的350行,TimeCompilations默认为1,可以通过隐藏的选项“-time-compilations”来指定它的值,它的作用是重复进行指定次数的编译,以得到更好的编译用时数据。而在这个循环中调用的compileModule()&a…...
C语言 每日一题 PTA 10.30 day8
1.高空坠球 皮球从某给定高度自由落下,触地后反弹到原高度的一半,再落下,再反弹,……,如此反复。问皮球在第n次落地时,在空中一共经过多少距离?第n次反弹的高度是多少? 输入格式 : …...
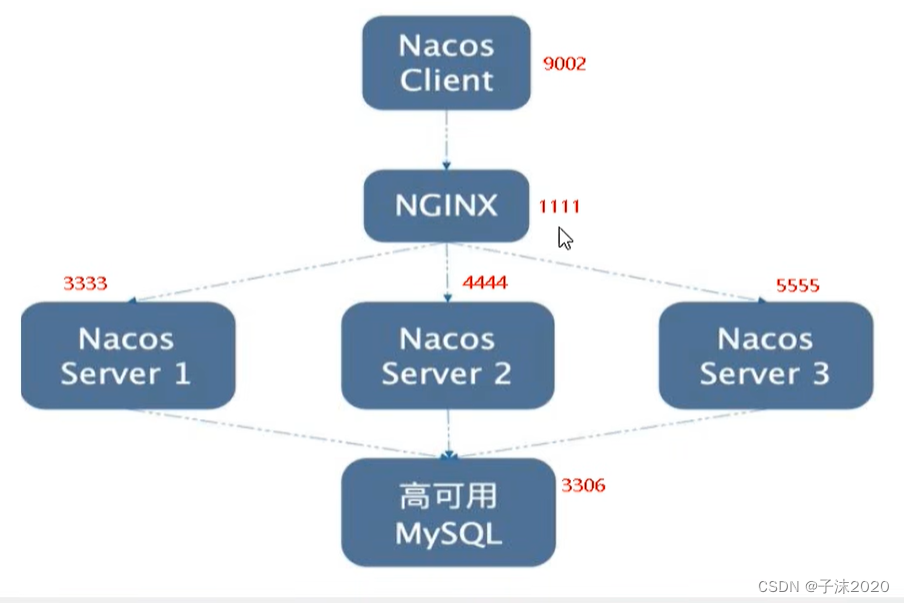
nacos在linux中的安装、集群的配置、mysql生产配置
1.下载和安装 官方下载地址:https://github.com/alibaba/nacos/releases,根据自己需要的本版去下载就行 下载的是 .tar.gz 后缀的文件是linux版本的 使用tar命令解压,完成之后是一个nacos的文件夹 和windows下的文件夹目录是一样的 要启…...

OpenAI 组建安全 AGI 新团队!应对AI“潘多拉魔盒”
夕小瑶科技说 原创 作者 | 小戏 一旦谈及未来 AI,除了天马行空的科幻畅想,不可避免的也有未来 AI 时代的末日预言。从 AI 武器化到 AI 欺骗,从邪恶 AI 到 AI 掌权,人工智能,尤其是通用人工智能的风险始终都清清楚楚的…...
上网行为管理软件有哪些丨功能图文超详细介绍
很多人都在后台问,上网行为管理软件到底是什么,有什么作用,今天就重点给大家讲解一下: 是什么 上网行为管理软件可以帮助企业规范员工的上网行为,提高办公效率,减少潜在威胁。 有哪些 在市面上ÿ…...
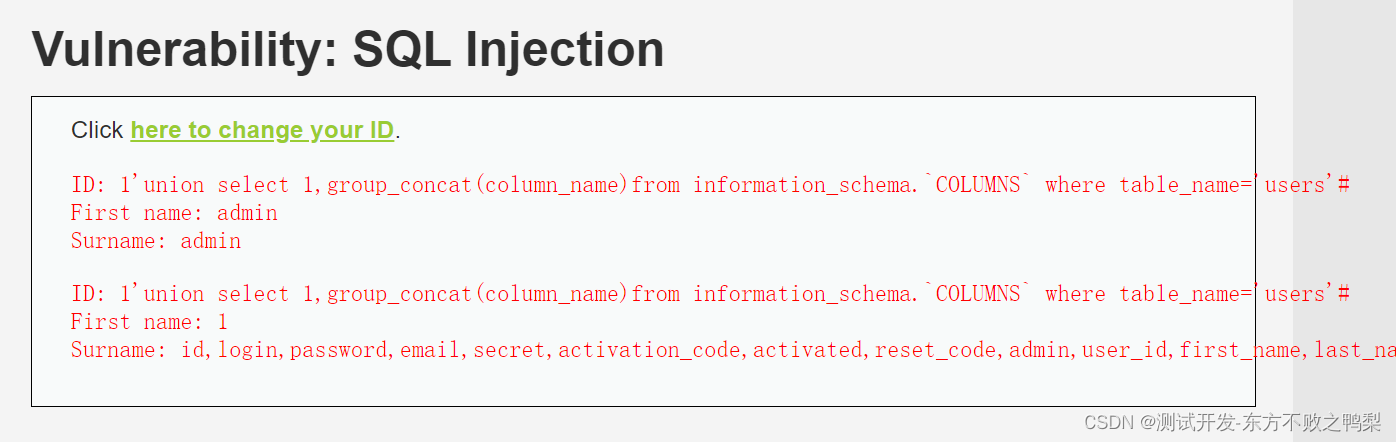
DVWA-SQL Injection SQL注入
概念 SQL注入,是指将特殊构造的恶意SQL语句插入Web表单的输入或页面请求的查询字符串中,从而欺骗后端Web服务器以执行该恶意SQL语句。 成功的 SQL 注入漏洞可以从数据库中读取敏感数据、修改数据库数据(插入/更新/删除)、对数据…...

【0基础学Java第四课】-- 逻辑控制
4. 逻辑控制 4.1 顺序结构4.2 分支结构4.2.1 if语句判断一个数字是奇数还是偶数判断一个数字是正数,负数,还是零判断一个年份是否为闰年 4.2.2 switch 语句 4.3 while循环打印 1 - 10 的数字计算 1 - 100 的和计算 5 的阶乘计算1!2࿰…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...

门静脉高压——表现
一、门静脉高压表现 00:01 1. 门静脉构成 00:13 组成结构:由肠系膜上静脉和脾静脉汇合构成,是肝脏血液供应的主要来源。淤血后果:门静脉淤血会同时导致脾静脉和肠系膜上静脉淤血,引发后续系列症状。 2. 脾大和脾功能亢进 00:46 …...

Canal环境搭建并实现和ES数据同步
作者:田超凡 日期:2025年6月7日 Canal安装,启动端口11111、8082: 安装canal-deployer服务端: https://github.com/alibaba/canal/releases/1.1.7/canal.deployer-1.1.7.tar.gz cd /opt/homebrew/etc mkdir canal…...
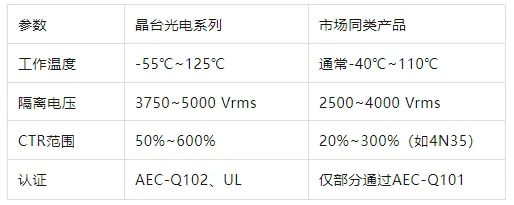
高抗扰度汽车光耦合器的特性
晶台光电推出的125℃光耦合器系列产品(包括KL357NU、KL3H7U和KL817U),专为高温环境下的汽车应用设计,具备以下核心优势和技术特点: 一、技术特性分析 高温稳定性 采用先进的LED技术和优化的IC设计,确保在…...
