【贝叶斯回归】【第 2 部分】--推理算法

一、说明
在第一部分中,我们研究了如何使用 SVI 对简单的贝叶斯线性回归模型进行推理。在本教程中,我们将探索更具表现力的指南以及精确的推理技术。我们将使用与之前相同的数据集。
二、模块导入
[1]:
%reset -sf
[2]:
import logging
import osimport torch
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from torch.distributions import constraintsimport pyro
import pyro.distributions as dist
import pyro.optim as optimpyro.set_rng_seed(1)
assert pyro.__version__.startswith('1.8.6')
[3]:
%matplotlib inline
plt.style.use('default')logging.basicConfig(format='%(message)s', level=logging.INFO)
smoke_test = ('CI' in os.environ)
pyro.set_rng_seed(1)
DATA_URL = "https://d2hg8soec8ck9v.cloudfront.net/datasets/rugged_data.csv"
rugged_data = pd.read_csv(DATA_URL, encoding="ISO-8859-1") 三、贝叶斯线性回归
我们的目标是再次根据数据集中的两个特征(该国家是否位于非洲及其地形坚固指数)来预测一个国家的人均 GDP 对数,但我们将探索更具表现力的指南。
3.1 模型+指南
我们将再次写出模型,类似于第一部分,但明确不使用 PyroModule。我们将使用相同的先验写出回归中的每一项。 bA和bR是is_cont_africa和roughness对应的回归系数,a是截距,bAR是两个特征之间的相关因子。
编写指南的过程与我们模型的构建非常相似,主要区别在于指南参数需要可训练。为此,我们使用在 ParamStore 中注册指南参数pyro.param()。注意尺度参数的正约束。
[4]:
def model(is_cont_africa, ruggedness, log_gdp):a = pyro.sample("a", dist.Normal(0., 10.))b_a = pyro.sample("bA", dist.Normal(0., 1.))b_r = pyro.sample("bR", dist.Normal(0., 1.))b_ar = pyro.sample("bAR", dist.Normal(0., 1.))sigma = pyro.sample("sigma", dist.Uniform(0., 10.))mean = a + b_a * is_cont_africa + b_r * ruggedness + b_ar * is_cont_africa * ruggednesswith pyro.plate("data", len(ruggedness)):pyro.sample("obs", dist.Normal(mean, sigma), obs=log_gdp)def guide(is_cont_africa, ruggedness, log_gdp):a_loc = pyro.param('a_loc', torch.tensor(0.))a_scale = pyro.param('a_scale', torch.tensor(1.),constraint=constraints.positive)sigma_loc = pyro.param('sigma_loc', torch.tensor(1.),constraint=constraints.positive)weights_loc = pyro.param('weights_loc', torch.randn(3))weights_scale = pyro.param('weights_scale', torch.ones(3),constraint=constraints.positive)a = pyro.sample("a", dist.Normal(a_loc, a_scale))b_a = pyro.sample("bA", dist.Normal(weights_loc[0], weights_scale[0]))b_r = pyro.sample("bR", dist.Normal(weights_loc[1], weights_scale[1]))b_ar = pyro.sample("bAR", dist.Normal(weights_loc[2], weights_scale[2]))sigma = pyro.sample("sigma", dist.Normal(sigma_loc, torch.tensor(0.05)))mean = a + b_a * is_cont_africa + b_r * ruggedness + b_ar * is_cont_africa * ruggedness
[5]:
# Utility function to print latent sites' quantile information.
def summary(samples):site_stats = {}for site_name, values in samples.items():marginal_site = pd.DataFrame(values)describe = marginal_site.describe(percentiles=[.05, 0.25, 0.5, 0.75, 0.95]).transpose()site_stats[site_name] = describe[["mean", "std", "5%", "25%", "50%", "75%", "95%"]]return site_stats# Prepare training data
df = rugged_data[["cont_africa", "rugged", "rgdppc_2000"]]
df = df[np.isfinite(df.rgdppc_2000)]
df["rgdppc_2000"] = np.log(df["rgdppc_2000"])
train = torch.tensor(df.values, dtype=torch.float)
3.2 SVI推理
和之前一样,我们将使用 SVI 来执行推理。
[6]:
from pyro.infer import SVI, Trace_ELBOsvi = SVI(model,guide,optim.Adam({"lr": .05}),loss=Trace_ELBO())is_cont_africa, ruggedness, log_gdp = train[:, 0], train[:, 1], train[:, 2]
pyro.clear_param_store()
num_iters = 5000 if not smoke_test else 2
for i in range(num_iters):elbo = svi.step(is_cont_africa, ruggedness, log_gdp)if i % 500 == 0:logging.info("Elbo loss: {}".format(elbo))
埃尔博损失:5795.467590510845
埃尔博损失:415.8169444799423
埃尔博损失:250.71916329860687
埃尔博损失:247.19457268714905
埃尔博损失:249.2004036307335
埃尔博损失:250.96484470367432
埃尔博损失:249.35092514753342
埃尔博损失:248.7831552028656
埃尔博损失:248.62140649557114
埃尔博损失:250.4274433851242
[7]:
from pyro.infer import Predictivenum_samples = 1000
predictive = Predictive(model, guide=guide, num_samples=num_samples)
svi_samples = {k: v.reshape(num_samples).detach().cpu().numpy()for k, v in predictive(log_gdp, is_cont_africa, ruggedness).items()if k != "obs"}
让我们观察模型中不同潜在变量的后验分布。
[8]:
for site, values in summary(svi_samples).items():print("Site: {}".format(site))print(values, "\n")
站点:a平均标准差 5% 25% 50% 75% 95%
0 9.177024 0.059607 9.07811 9.140463 9.178211 9.217098 9.27152地点:bA平均标准差 5% 25% 50% 75% 95%
0 -1.890622 0.122805 -2.08849 -1.979107 -1.887476 -1.803683 -1.700853站点:bR平均标准差 5% 25% 50% 75% 95%
0 -0.157847 0.039538 -0.22324 -0.183673 -0.157873 -0.133102 -0.091713站点:bAR平均标准差 5% 25% 50% 75% 95%
0 0.304515 0.067683 0.194583 0.259464 0.304907 0.348932 0.415128网站:西格玛平均标准差 5% 25% 50% 75% 95%
0 0.902898 0.047971 0.824166 0.870317 0.901981 0.935171 0.981577 3.3 HMC
与使用变分推理(为我们提供潜在变量的近似后验)相反,我们还可以使用马尔可夫链蒙特卡罗(MCMC)进行精确推理,这是一类算法,在极限情况下,允许我们从真实的样本中提取无偏样本。后部。我们将使用的算法称为 No-U Turn Sampler (NUTS) [1],它提供了一种运行哈密顿蒙特卡罗的高效且自动化的方法。它比变分推理稍慢,但提供了精确的估计。
[9]:
from pyro.infer import MCMC, NUTSnuts_kernel = NUTS(model)mcmc = MCMC(nuts_kernel, num_samples=1000, warmup_steps=200)
mcmc.run(is_cont_africa, ruggedness, log_gdp)hmc_samples = {k: v.detach().cpu().numpy() for k, v in mcmc.get_samples().items()}
样本:100%|██████████| 1200/1200 [00:30,38.99it/s,步长=2.76e-01,根据。概率=0.934]
[10]:
for site, values in summary(hmc_samples).items():print("Site: {}".format(site))print(values, "\n")
站点:a平均标准差 5% 25% 50% 75% 95%
0 9.182098 0.13545 8.958712 9.095588 9.181347 9.277673 9.402615地点:bA平均标准差 5% 25% 50% 75% 95%
0 -1.847651 0.217768 -2.19934 -1.988024 -1.846978 -1.70495 -1.481822站点:bR平均标准差 5% 25% 50% 75% 95%
0 -0.183031 0.078067 -0.311403 -0.237077 -0.185945 -0.131043 -0.051233站点:bAR平均标准差 5% 25% 50% 75% 95%
0 0.348332 0.127478 0.131907 0.266548 0.34641 0.427984 0.560221网站:西格玛平均标准差 5% 25% 50% 75% 95%
0 0.952041 0.052024 0.869388 0.914335 0.949961 0.986266 1.038723 3.4 比较后验分布
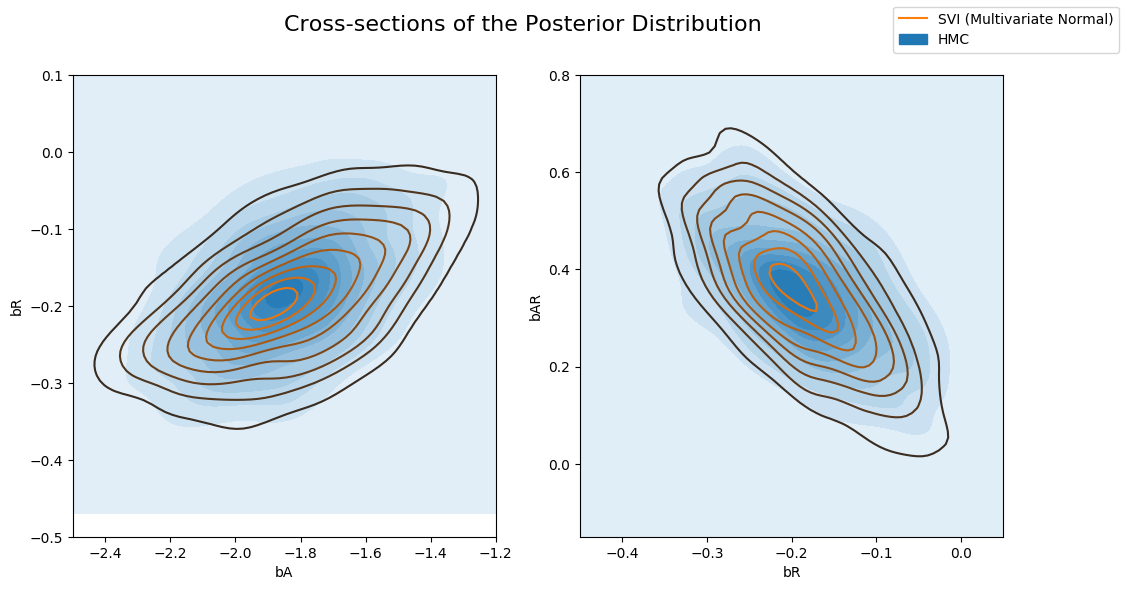
让我们将通过变分推理获得的潜在变量的后验分布与哈密顿蒙特卡罗获得的潜在变量的后验分布进行比较。如下所示,对于变分推理,不同回归系数的边缘分布相对于真实后验(来自 HMC)而言是分散不足的。这是通过变分推理最小化的KL(q||p)损失(真实后验与近似后验的 KL 散度)的伪影。
当我们绘制来自联合后验分布的不同横截面并覆盖来自变分推理的近似后验时,可以更好地看到这一点。请注意,由于我们的变分族具有对角协方差,因此我们无法对潜在变量之间的任何相关性进行建模,并且所得的近似值过于自信(分散不足)
[11]:
sites = ["a", "bA", "bR", "bAR", "sigma"]fig, axs = plt.subplots(nrows=2, ncols=2, figsize=(12, 10))
fig.suptitle("Marginal Posterior density - Regression Coefficients", fontsize=16)
for i, ax in enumerate(axs.reshape(-1)):site = sites[i]sns.distplot(svi_samples[site], ax=ax, label="SVI (DiagNormal)")sns.distplot(hmc_samples[site], ax=ax, label="HMC")ax.set_title(site)
handles, labels = ax.get_legend_handles_labels()
fig.legend(handles, labels, loc='upper right');

[12]:
fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(12, 6))
fig.suptitle("Cross-section of the Posterior Distribution", fontsize=16)
sns.kdeplot(x=hmc_samples["bA"], y=hmc_samples["bR"], ax=axs[0], shade=True, label="HMC")
sns.kdeplot(x=svi_samples["bA"], y=svi_samples["bR"], ax=axs[0], label="SVI (DiagNormal)")
axs[0].set(xlabel="bA", ylabel="bR", xlim=(-2.5, -1.2), ylim=(-0.5, 0.1))
sns.kdeplot(x=hmc_samples["bR"], y=hmc_samples["bAR"], ax=axs[1], shade=True, label="HMC")
sns.kdeplot(x=svi_samples["bR"], y=svi_samples["bAR"], ax=axs[1], label="SVI (DiagNormal)")
axs[1].set(xlabel="bR", ylabel="bAR", xlim=(-0.45, 0.05), ylim=(-0.15, 0.8))
handles, labels = axs[1].get_legend_handles_labels()
fig.legend(handles, labels, loc='upper right');

3.5 多元正态指南
与之前从对角正态指南获得的结果相比,我们现在将使用从多元正态分布的 Cholesky 分解生成样本的指南。这使我们能够通过协方差矩阵捕获潜在变量之间的相关性。如果我们手动编写此代码,我们将需要组合所有潜在变量,以便我们可以联合采样多元正态分布。
[13]:
from pyro.infer.autoguide import AutoMultivariateNormal, init_to_meanguide = AutoMultivariateNormal(model, init_loc_fn=init_to_mean)svi = SVI(model,guide,optim.Adam({"lr": .01}),loss=Trace_ELBO())is_cont_africa, ruggedness, log_gdp = train[:, 0], train[:, 1], train[:, 2]
pyro.clear_param_store()
for i in range(num_iters):elbo = svi.step(is_cont_africa, ruggedness, log_gdp)if i % 500 == 0:logging.info("Elbo loss: {}".format(elbo))
埃尔博损失:703.0100790262222
埃尔博损失:444.6930855512619
埃尔博损失:258.20718491077423
埃尔博损失:249.05364602804184
埃尔博损失:247.2170884013176
埃尔博损失:247.28261297941208
埃尔博损失:246.61236548423767
埃尔博损失:249.86004841327667
埃尔博损失:249.1157277226448
埃尔博损失:249.86634194850922
我们再看一下后背的形状。您可以看到多变量指南能够捕获更多真实的后验信息。
[14]:
predictive = Predictive(model, guide=guide, num_samples=num_samples)
svi_mvn_samples = {k: v.reshape(num_samples).detach().cpu().numpy()for k, v in predictive(log_gdp, is_cont_africa, ruggedness).items()if k != "obs"}
fig, axs = plt.subplots(nrows=2, ncols=2, figsize=(12, 10))
fig.suptitle("Marginal Posterior density - Regression Coefficients", fontsize=16)
for i, ax in enumerate(axs.reshape(-1)):site = sites[i]sns.distplot(svi_mvn_samples[site], ax=ax, label="SVI (Multivariate Normal)")sns.distplot(hmc_samples[site], ax=ax, label="HMC")ax.set_title(site)
handles, labels = ax.get_legend_handles_labels()
fig.legend(handles, labels, loc='upper right');

现在让我们比较对角法线引导和多元法线引导计算的后验。请注意,多元分布比对角正态分布更不均匀。
[15]:
fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(12, 6))
fig.suptitle("Cross-sections of the Posterior Distribution", fontsize=16)
sns.kdeplot(x=svi_samples["bA"], y=svi_samples["bR"], ax=axs[0], label="SVI (Diagonal Normal)")
sns.kdeplot(x=svi_mvn_samples["bA"], y=svi_mvn_samples["bR"], ax=axs[0], shade=True, label="SVI (Multivariate Normal)")
axs[0].set(xlabel="bA", ylabel="bR", xlim=(-2.5, -1.2), ylim=(-0.5, 0.1))
sns.kdeplot(x=svi_samples["bR"], y=svi_samples["bAR"], ax=axs[1], label="SVI (Diagonal Normal)")
sns.kdeplot(x=svi_mvn_samples["bR"], y=svi_mvn_samples["bAR"], ax=axs[1], shade=True, label="SVI (Multivariate Normal)")
axs[1].set(xlabel="bR", ylabel="bAR", xlim=(-0.45, 0.05), ylim=(-0.15, 0.8))
handles, labels = axs[1].get_legend_handles_labels()
fig.legend(handles, labels, loc='upper right');

以及由 HMC 计算后验的多变量指南。请注意,多变量指南可以更好地捕获真实的后验。
[16]:
fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(12, 6))
fig.suptitle("Cross-sections of the Posterior Distribution", fontsize=16)
sns.kdeplot(x=hmc_samples["bA"], y=hmc_samples["bR"], ax=axs[0], shade=True, label="HMC")
sns.kdeplot(x=svi_mvn_samples["bA"], y=svi_mvn_samples["bR"], ax=axs[0], label="SVI (Multivariate Normal)")
axs[0].set(xlabel="bA", ylabel="bR", xlim=(-2.5, -1.2), ylim=(-0.5, 0.1))
sns.kdeplot(x=hmc_samples["bR"], y=hmc_samples["bAR"], ax=axs[1], shade=True, label="HMC")
sns.kdeplot(x=svi_mvn_samples["bR"], y=svi_mvn_samples["bAR"], ax=axs[1], label="SVI (Multivariate Normal)")
axs[1].set(xlabel="bR", ylabel="bAR", xlim=(-0.45, 0.05), ylim=(-0.15, 0.8))
handles, labels = axs[1].get_legend_handles_labels()
fig.legend(handles, labels, loc='upper right');
参考
[1] 霍夫曼、马修·D.和安德鲁·格尔曼。“禁止掉头采样器:在哈密顿蒙特卡罗中自适应设置路径长度。” 机器学习研究杂志 15.1(2014):1593-1623。https://arxiv.org/abs/1111.4246。
相关文章:

【贝叶斯回归】【第 2 部分】--推理算法
一、说明 在第一部分中,我们研究了如何使用 SVI 对简单的贝叶斯线性回归模型进行推理。在本教程中,我们将探索更具表现力的指南以及精确的推理技术。我们将使用与之前相同的数据集。 二、模块导入 [1]:%reset -sf[2]:import logging import osimport tor…...

【深入浅出汇编语言】寄存器精讲第二期
🌈个人主页:聆风吟 🔥系列专栏:数据结构、算法模板、汇编语言 🔖少年有梦不应止于心动,更要付诸行动。 文章目录 📋前言一. ⛳️物理地址二. ⛳️16位结构的CPU三. ⛳️8086CPU给出物理地址的方…...

如何保证分布式情况下的幂等性
关于这个分布式服务的幂等性,这是在使用分布式服务的时候会经常遇到的问题,比如,重复提交的问题。而幂等性,就是为了解决问题存在的一个概念了。 什么是幂等 幂等(idempotent、idempotence)是⼀个数学与计算机学概念,常⻅于抽象代数中。 在编程中⼀个幂等操作的特点是…...

Mybatis特殊SQL的执行
文章目录 模糊查询批量删除动态设置表名添加功能获取自增的主键自定义映射resultMapresultMap处理字段和属性的映射关系 多对一映射处理级联方式处理映射关系使用association处理映射关系 分步查询1. 查询员工信息 2. 查询部门信息 一对多映射处理collection 模糊查询 /*** 根…...
MyBatis-Flex(一):快速开始
框架介绍 MyBatis-Flex 是一个优雅的 MyBatis 增强框架,它非常轻量、同时拥有极高的性能与灵活性。 MyBatis-Flex 官方文档 说明 本文参照官方文档的【快速开始】 章节,编写 Spring Boot 项目的代码示例。 快速开始 创建数据库表 直接参照官网示…...

Vue组件化
组件 组件是实现应用中局部功能的代码(HTML,CSS,JS)和资源(图片,声音,视频)的集合,凡是采用组件方式开发的应用都可以称为组件化应用 模块是指将一个大的js文件按照模块化拆分规则进行拆分成的每个js文件, 凡是采用模块方式开发的应用都可以称为模块化应用(组件包括模块) 传…...

nodejs+python+php+微信小程序-基于安卓android的健身服务应用APP-计算机毕业设计
考虑到实际生活中在健身服务应用方面的需要以及对该系统认真的分析,将系统权限按管理员和用户这两类涉及用户划分。 则对于进一步提高健身服务应用发展,丰富健身服务应用经验能起到不少的促进作用。 健身服务应用APP能够通过互联网得到广泛的、全面的宣…...
SpringCloud 微服务全栈体系(九)
第九章 Docker 三、Dockerfile 自定义镜像 常见的镜像在 DockerHub 就能找到,但是我们自己写的项目就必须自己构建镜像了。 而要自定义镜像,就必须先了解镜像的结构才行。 1. 镜像结构 镜像是将应用程序及其需要的系统函数库、环境、配置、依赖打包而…...
Mybatis 多对一和一对多查询
文章目录 Mybatis 多对一 and 一对多查询详解数据库需求Mybatis代码注意 Mybatis 多对一 and 一对多查询详解 数据库 员工表 t_emp 部门表 t_dept CREATE TABLE t_emp (emp_id int NOT NULL AUTO_INCREMENT,emp_name varchar(25) CHARACTER SET utf8 COLLATE utf8_general_ci…...
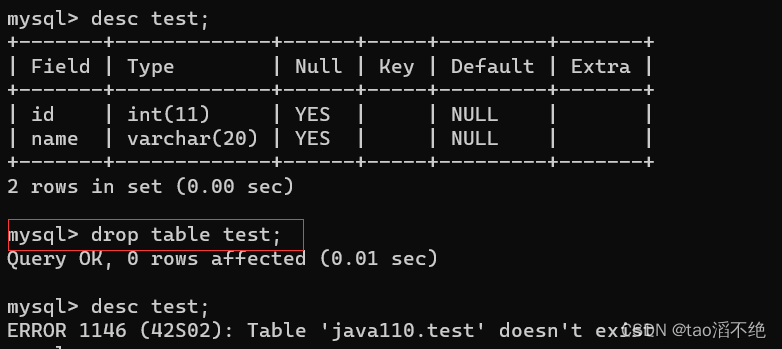
MySQL的数据库操作、数据类型、表操作
目录 一、数据库操作 (1)、显示数据库 (2)、创建数据库 (3)、删除数据库 (4)、使用数据库 二、常用数据类型 (1)、数值类型 (2࿰…...

音视频技术开发周刊 | 317
每周一期,纵览音视频技术领域的干货。 新闻投稿:contributelivevideostack.com。 MIT惊人再证大语言模型是世界模型!LLM能分清真理和谎言,还能被人类洗脑 MIT等学者的「世界模型」第二弹来了!这次,他们证明…...

【JavaSE专栏58】“Java构造函数:作用、类型、调用顺序和最佳实践“ ⚙️⏱️
解析Java构造函数:作用、类型、调用顺序和最佳实践" 🚀📚🔍🤔📝🔄⚙️⏱️📖🌐 摘要引言1. 什么是构造函数 🤔2. 构造函数的类型与用途 📝1.…...
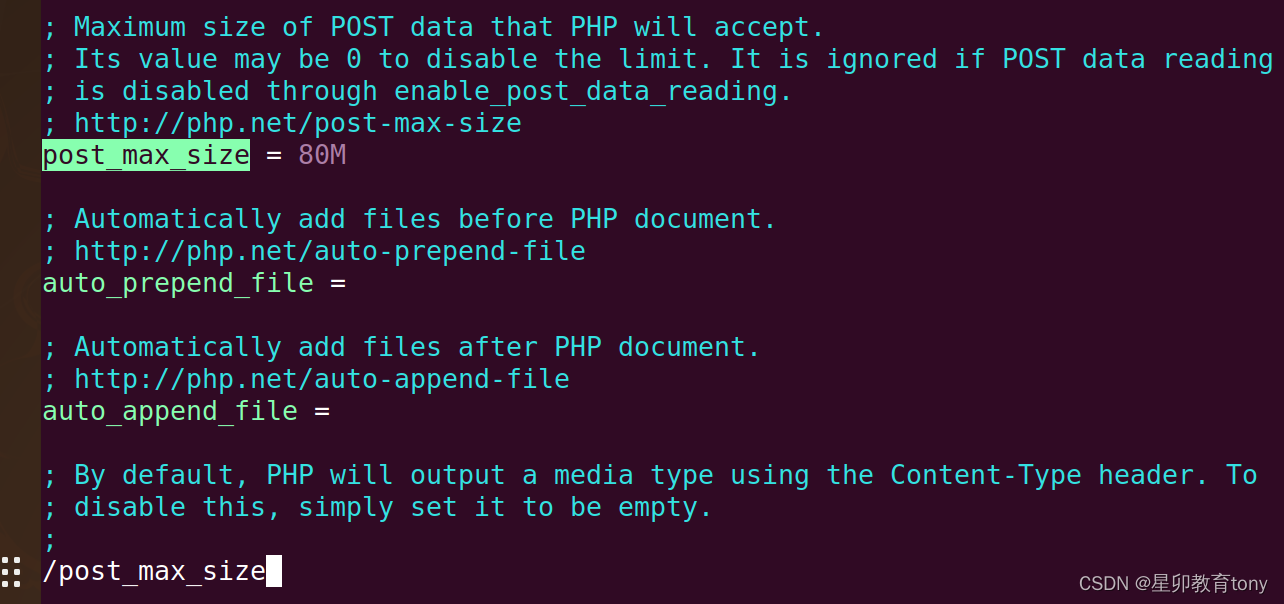
Ubuntu系统HUSTOJ 用 vim 修改php.ini 重启PHP服务
cd / sudo find -name php.ini 输出: ./etc/php/7.4/cli/php.ini ./etc/php/7.4/fpm/php.ini sudo vim /etc/php/7.4/cli/php.ini sudo vim /etc/php/7.4/fpm/php.ini 知识准备: vim的搜索与替换 在正常模式下键入 / ,即可进入搜索模式…...

案例分析真题-信息安全
案例分析真题-信息安全 2009年真题 【问题1】 【问题2】 【问题3】 2010年真题 【问题1】 【问题2】 【问题3】 2011 年真题 【问题1】 【问题2】 【问题3】 骚戴理解:这个破题目完全考的知识储备,不知道的连手都动不了,没法分析 2013年真题…...
envi5.3处理高分二号影像数据辐射定标大气校正
目录 一、多光谱影像处理 1. 辐射定标 2.大气校正 1. 需要准备一些数据: 2.大气校正过程 3、正射校正 二、全色影像处理 1. 辐射定标 2. 正射校正 三、图像融合 1.几何配准 2.图像融合 高分二号处理流程 envi5.3的安装教程: ENVI5.3安装 安装完ENVI5.3后࿰…...

C语言 结构体
结构体的自引用: 自引用的目的: 结构体的自引用就是指在结构体内部,包含指向自身类型结构体的指针。 像链表就会用到结构体的自引用。假如我们要创建链表 链表的没个节点都是一个结构体,它里面存放着它的数据和下个节点的地址。 假如我们用…...

frp-内网穿透部署-ubuntu22服务器-windows server-详细教程
文章目录 1.下载frp2.配置服务器2.1.配置frps.ini文件2.2.设置服务文件2.3.设置开机自启和服务操作2.4.后台验证2.5.服务器重启 3.配置本地window3.1.frpc配置3.2.添加开机计划启动3.3.控制台启动隐藏窗口 4.centos防火墙和端口3.1.开放端口3.2.查看端口 5.关闭进程5.1.杀死进程…...

MySQL内存使用的监控开关和使用查看
参考文档: https://brands.cnblogs.com/tencentcloud/p/11151 https://www.cnblogs.com/grasp/p/10306697.html MySQL如何使用内存 在MySQL中,内存占用主要包括以下几部分,全局共享的内存、线程独占的内存、内存分配器占用的内存࿰…...
数据库管理-第113期 Oracle Exadata 04-硬件选择(20231020)
数据库管理-第113期 Oracle Exadata 04-硬件选择(2023010290) 本周没写文章,主要是因为到上海参加了Oracle CAB/PAB会议,这个放在后面再讲,本期讲一讲Exadata,尤其是存储节点的硬件选择及其对应的一些通用…...
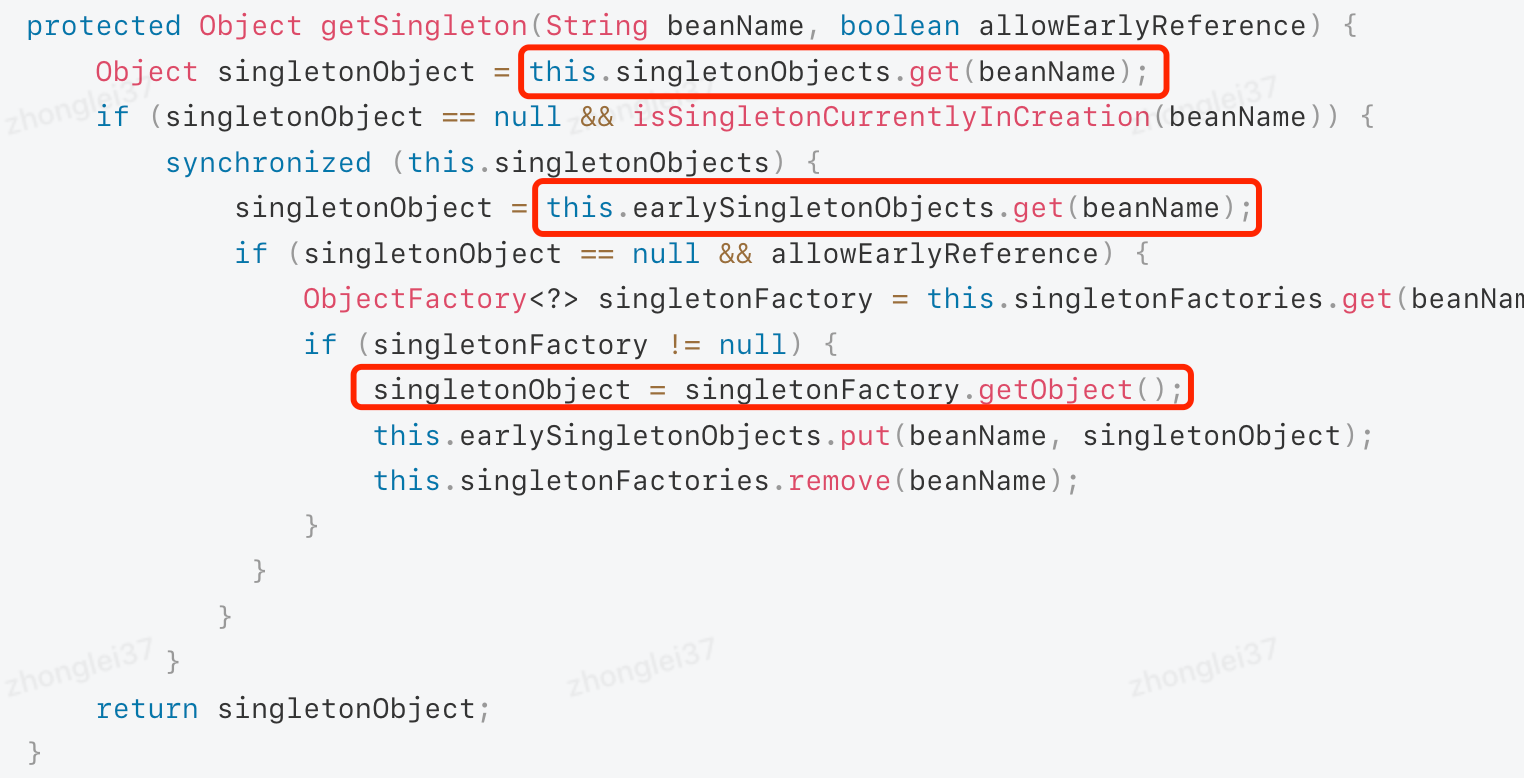
带着问题去分析:Spring Bean 生命周期 | 京东物流技术团队
1: Bean在Spring容器中是如何存储和定义的 Bean在Spring中的定义是_org.springframework.beans.factory.config.BeanDefinition_接口,BeanDefinition里面存储的就是我们编写的Java类在Spring中的元数据,包括了以下主要的元数据信息: 1&…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...
