Python稀疏矩阵最小二乘法
文章目录
- 最小二乘法
- 返回值
- 测试
最小二乘法
scipy.sparse.linalg实现了两种稀疏矩阵最小二乘法lsqr和lsmr,前者是经典算法,后者来自斯坦福优化实验室,据称可以比lsqr更快收敛。
这两个函数可以求解Ax=bAx=bAx=b,或arg minx∥Ax−b∥2\argmin_x\Vert Ax-b\Vert^2argminx∥Ax−b∥2,或arg minx∥Ax−b∥2+d2∥x−x0∥2\argmin_x\Vert Ax-b\Vert^2+d^2\Vert x-x_0\Vert^2argminx∥Ax−b∥2+d2∥x−x0∥2,其中AAA必须是方阵或三角阵,可以有任意秩。
通过设置容忍度at,bta_t, b_tat,bt,可以控制算法精度,记r=b−Axr=b-Axr=b−Ax为残差向量,如果Ax=bAx=bAx=b是相容的,lsqr在∥r∥⩽at∗∥A∥⋅∥x∥+bt∥b∥\Vert r\Vert\leqslant a_t*\Vert A\Vert\cdot\Vert x\Vert + b_t\Vert b\Vert∥r∥⩽at∗∥A∥⋅∥x∥+bt∥b∥时终止;否则将在∥ATr∥⩽at∥A∥⋅∥r∥\Vert A^T r\Vert\leqslant a_t\Vert A\Vert \cdot\Vert r\Vert∥ATr∥⩽at∥A∥⋅∥r∥。
如果两个容忍度都是10−610^{-6}10−6,最终的∥r∥\Vert r\Vert∥r∥将有6位精度。
lsmr的参数如下
lsmr(A, b, damp=0.0, atol=1e-06, btol=1e-06, conlim=100000000.0, maxiter=None, show=False, x0=None)
参数解释:
A可谓稀疏矩阵、数组以及线性算子b为数组damp阻尼系数,默认为0atol,btol截止容忍度,是lsqr迭代的停止条件,即at,bta_t, b_tat,bt。conlim另一个截止条件,对于最小二乘问题,conlim应该小于10810^8108,如果Ax=bAx=bAx=b是相容的,则conlim最大可以设到101210^{12}1012iter_limint迭代次数show如果为True,则打印运算过程calc_var是否估计(A.T@A + damp**2*I)^{-1}的对角线x0阻尼系数相关
lsqr和lsmr相比,没有maxiter参数,但多了iter_lim, calc_va参数。
上述参数中,damp为阻尼系数,当其不为0时,记作δ\deltaδ,待解决的最小二乘问题变为
[AδI]x=[bδx0]\begin{bmatrix}A\\\delta I\end{bmatrix} x=\begin{bmatrix}b\\\delta x_0 \end{bmatrix} [AδI]x=[bδx0]
返回值
lsmr的返回值依次为:
x即Ax=bAx=bAx=b中的xxxistop程序结束运行的原因itn迭代次数normr∥b−Ax∥\Vert b-Ax\Vert∥b−Ax∥normar∥AT(b−Ax)∥\Vert A^T(b-Ax)\Vert∥AT(b−Ax)∥norma∥A∥\Vert A\Vert∥A∥condaA的条件数normx∥x∥\Vert x\Vert∥x∥
lsqr的返回值为
x即Ax=bAx=bAx=b中的xxxistop程序结束运行的原因itn迭代次数r1norm∥b−Ax∥\Vert b-Ax\Vert∥b−Ax∥r2norm∥b−Ax∥2+δ2∥x−x0∥2\sqrt{\Vert b-Ax\Vert^2+\delta^2\Vert x-x_0\Vert^2}∥b−Ax∥2+δ2∥x−x0∥2anorm估计的Frobenius范数Aˉ\bar AAˉacondAˉ\bar AAˉ的条件数arnorm∥ATr−δ2(x−x0)∥\Vert A^Tr-\delta^2(x-x_0)\Vert∥ATr−δ2(x−x0)∥xnorm∥x∥\Vert x\Vert∥x∥var(ATA)−1(A^TA)^{-1}(ATA)−1
二者的返回值较多,而且除了前四个之外,剩下的意义不同,调用时且须注意。
测试
下面对这两种算法进行验证,第一步就得先有一个稀疏矩阵
import numpy as np
from scipy.sparse import csr_arraynp.random.seed(42) # 设置随机数状态
mat = np.random.rand(500,500)
mat[mat<0.9] = 0
csr = csr_array(mat)
然后用这个稀疏矩阵乘以一个xxx,得到bbb
xs = np.arange(500)
b = mat @ xs
接下来对这两个最小二乘函数进行测试
from scipy.sparse.linalg import lsmr, lsqr
import matplotlib.pyplot as plt
mx = lsmr(csr, b)[0]
qx = lsqr(csr, b)[0]
plt.plot(xs, lw=0.5)
plt.plot(mx, lw=0, marker='*', label="lsmr")
plt.plot(qx, lw=0, marker='.', label="lsqr")
plt.legend()
plt.show()
为了对比清晰,对图像进行放大,可以说二者不分胜负

接下来比较二者的效率,500×500500\times500500×500这个尺寸显然已经不合适了,用2000×20002000\times20002000×2000
from timeit import timeitnp.random.seed(42) # 设置随机数状态
mat = np.random.rand(500,500)
mat[mat<0.9] = 0
csr = csr_array(mat)
timeit(lambda : lsmr(csr, b), number=10)
timeit(lambda : lsqr(csr, b), number=10)
测试结果如下
>>> timeit(lambda : lsqr(csr, b), number=10)
0.5240591000001587
>>> timeit(lambda : lsmr(csr, b), number=10)
0.6156221000019286
看来lsmr并没有更快,看来斯坦福也不靠谱(滑稽)。
相关文章:

Python稀疏矩阵最小二乘法
文章目录最小二乘法返回值测试最小二乘法 scipy.sparse.linalg实现了两种稀疏矩阵最小二乘法lsqr和lsmr,前者是经典算法,后者来自斯坦福优化实验室,据称可以比lsqr更快收敛。 这两个函数可以求解AxbAxbAxb,或arg minx∥Ax−b…...

mac本前端Homebrew下载,操作
1、打开电脑终端 2、下载Homebrew,在终端中输入 /usr/bin/ruby -e "$(curl -fsSL https://raw.githubusercontent.com/Homebrew/install/master/install)"开始下载Homebrew,因为这个地址是国外网站,下载失败的话,输入…...

Linux系统之查看进程监听端口方法
Linux系统之查看进程监听端口方法一、端口监听介绍二、使用netstat命令1.netstat命令介绍2.netstat帮助3.安装netstat工具4.列出所有监听 tcp 端口5.显示TCP端口的统计信息6.查看某个服务监听端口三、使用ss命令1.ss命令介绍2.ss命令帮助3.查看某个服务监听端口四、使用lsof命令…...
使用命令别名一键启动arthas
1. 使用命令别名启动arthas 确保单板上有jdk和arthas jdk目录:/home/xinliushijian/arthas/jdk arthas目录;/home/xinliushijian/arthas su xinliushijian编写脚本messi.sh cd /home/xinliushijian/arthas vi messi.sh 内容如下: #!/bin/ba…...

python+pytest接口自动化(2)-HTTP协议基础
HTTP协议简介HTTP 即 HyperText Transfer Protocol(超文本传输协议),是互联网上应用最为广泛的一种网络协议。所有的 WWW 文件都必须遵守这个标准。设计 HTTP 最初的目的是为了提供一种发布和接收 HTML 页面的方法。HTTP 协议在 OSI 模型中属…...

操作系统权限提升(十五)之绕过UAC提权-基于白名单DLL劫持绕过UAC提权
系列文章 操作系统权限提升(十二)之绕过UAC提权-Windows UAC概述 操作系统权限提升(十三)之绕过UAC提权-MSF和CS绕过UAC提权 操作系统权限提升(十四)之绕过UAC提权-基于白名单AutoElevate绕过UAC提权 注:阅读本编文章前,请先阅读系列文章,以…...
非常好看的html网页个人简历
一. 前言 文末获取gitee链接 在前几天逛b站的时候,发现了个比较实用的东西-----个人简介网页版,相当于网页版的个人简历,相较于PDF形式的,网页版所能呈现内容更加丰富,而且更加美观,在BOOS上被HR小姐姐要…...
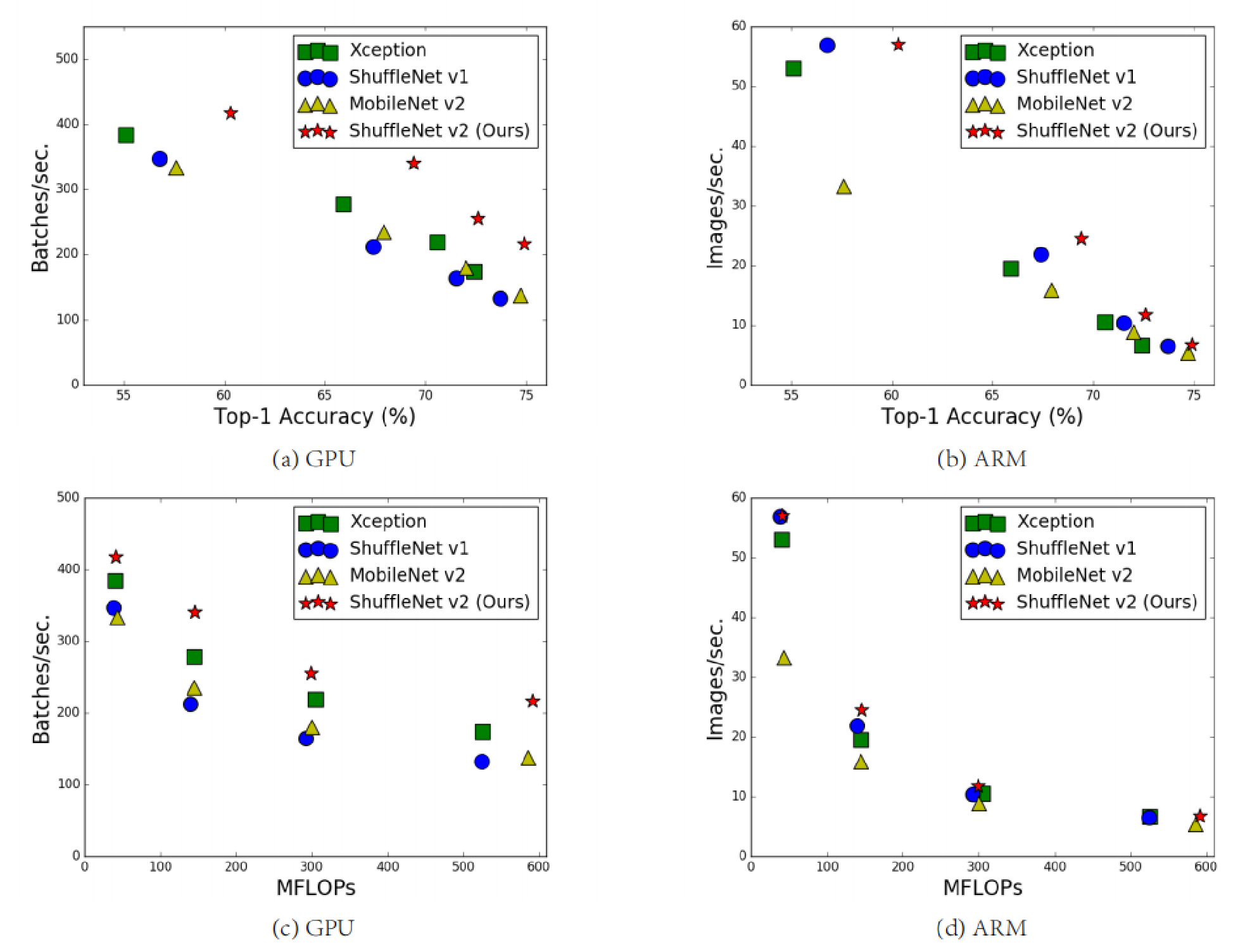
轻量级网络模型ShuffleNet V2
在学习ShuffleNet V2内容前需要简单了解卷积神经网络和MobileNet,以及Shuffnet V1的相关内容,大家可以出门左转,去看我之前的几篇博客MobileNet发展脉络(V1-V2-V3),轻量级网络模型ShuffleNet V1🆗ÿ…...
分享美容美发会员管理系统功能的特点_美容美发会员管理系统怎么做
人们越来越关心美发,美发行业发展迅速,小程序可以连接在线场景,许多美发院也开发了会员卡管理系统。那么一个实用的美发会员管理系统怎么制作呢?它有什么功能?我们一起来看看~(干货满满,耐心看完…...

Oracle-05-DCL篇
🏆一、简介 Oracle的DCL代表数据库控制语言,用于管理数据库对象的访问和安全性。DCL的两个主要命令是GRANT和REVOKE。 GRANT命令用于授予用户或角色对数据库对象的访问权限,例如表、视图或存储过程。GRANT命令的语法如下: GRANT privilege_name [, privilege_name]... …...

tess4j简单使用入门
tess4j下载 下载地址: https://sourceforge.net/projects/tess4j/ 不要直接下载,点击files,然后下载最新版 下载解压后放到指定的目录即可,这里放到d:\jar目录下 tess4j根目录: d:\jar\tess4j tess4j使用 把test4j项目目录中dist和lib目录下的所有jar包导入到需要的项目中…...

WebGPU学习(4)---使用 UniformBuffer
接下来让我们使用 UniformBuffer。UniformBuffer 是一个只读内存区域,可以在着色器上访问。 这次,我们将传递给着色器的矩阵存储在 UniformBuffer 中。演示示例 1.在顶点着色器中的 UniformBuffer 这次我们在顶点着色器里定义一个名为Uniforms的新结构体…...

Http客户端Feign-远程调用
Feign的使用步骤 引入依赖添加EnableFeignClients注解编写FeignClient接口使用FeignClient中定义的方法代替RestTemplate Feign的日志配置 1.方式一是配置文件,feign.client.config.xxx.loggerLevel 如果xxx是default则代表全局如果xxx是服务名称,例如userservi…...

RK3568镜像的拆包和打包
文章目录 前言一、window上分包和打包分包打包二、Linux上分包和打包分包打包总结前言 本文记录在win10上利用瑞芯微提供的工具进行分包和打包,同样也有Linux教程 提示:以下是本篇文章正文内容,下面案例可供参考 一、window上分包和打包 分包 window下一般直接利用工具即…...

《设计模式》适配器模式
《设计模式》适配器模式 适配器(Adapter)是一种结构型设计模式,它允许我们将一个类的接口转换成另一个类的接口,从而使得原本由于接口不兼容而无法合作的类能够一起工作。适配器模式通常用于以下情况: 在已有的类中添…...

linux 随笔 5-服务管理
0. 装到虚拟机与物理机,感觉各有各的不方便 Linux下systemctl命令和service、chkconfig命令的区别 1. service 根据/etc/init.d目录下的配置,做服务相关的: 启动停止重新启动关闭系统服务 2. chkconfig 用于维护 /etc/rc[0-6].d 的命令…...
【java基础】枚举类(enum)
文章目录基本介绍快速使用字段、方法、构造器枚举类方法toString方法valueOf方法values方法ordinal方法基本介绍 在java中有一种特殊的类型就是枚举类,对于一个有限的有固定值的集合,我们就可以考虑使用枚举类来进行表示,例如服装的大小为 小…...

Linux2
(1)root用户的主目录: (3)查看 (4)远程登陆系统:CentOS7上使用ifconfig查看IP,使用putty远程登陆 (5)查询目前用户登录情况:who命令…...

C语言基础应用(二)数据的转换与输入输出
学习了C语言的基本数据类型后,我们可能会想这些数据如何进行运算,是否可以让不同类型的数据直接进行运算呢? 一、数据类型转换 1.1 int类型与float类型之间的转换 int i 5; // j值为2.000000 因为左右操作数均为整型float j i/2; // …...
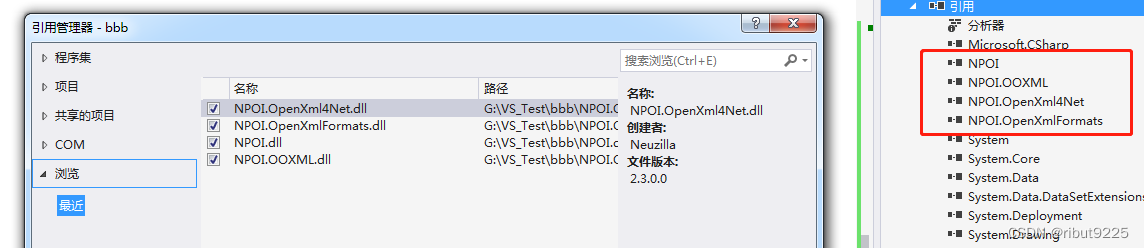
C# 用NPOI读取EXCEL
1. 复制DLL文件 ICSharpCode.SharpZipLib.dll NPOI.dll NPOI.OOXML.dll NPOI.OpenXml4Net.dll NPOI.OpenXmlFormats.dll 2. 在工程中添加引用 3. using System.IO; using NPOI.HSSF.UserModel; using NPOI.XSSF.UserModel; using NPOI.SS.UserModel; using NPOI.OpenXml4Ne…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...
