OpenCV 画极线
from pylab import *
import cv2from backend._gs_ import stereo_cameradef compute_epipole(F):""" 从基础矩阵 F 中计算右极点(可以使用 F.T 获得左极点)"""# 返回 F 的零空间(Fx=0)U,S,V = np.linalg.svd(F)e = V[-1]return e/e[2]def plot_epipolar_line(im, F, x, epipole=None, show_epipole=True):""" 在图像中,绘制外极点和外极线 F×x=0。F 是基础矩阵,x 是另一幅图像中的点 """m, n = im.shape[:2]line = np.dot(F, x)# 外极线参数和值t = np.linspace(0, n, 100)lt = np.array([(line[2] + line[0] * tt) / (-line[1]) for tt in t])# 仅仅处理位于图像内部的点和线ndx = (lt >= 0) & (lt < m)plot(t[ndx], lt[ndx], linewidth=2)if show_epipole:if epipole is None:epipole = compute_epipole(F)plot(epipole[0] / epipole[2], epipole[1] / epipole[2], 'r*')F = stereo_camera.F
im1 = cv2.imread(r'D:\mydocs\ftp\stereo_test\stereo_cali\small_test1\75_1.png')
im2 = cv2.imread(r'D:\mydocs\ftp\stereo_test\stereo_cali\small_test1\89_1.png')
x2 = np.array([ [1422, 1490, 1486], [1082,1183,1074], [1,1,1]])
# 计算极点
e = compute_epipole(F)# 绘制图像
figure()subplot(121)
imshow(im1)
# 分别绘制每个点,这样会绘制出和线同样的颜色
for i in range(3):plot(x2[0, i], x2[1, i], 'o')
title(u'outer polar')
axis('off')subplot(122)
imshow(im2)
# 分别绘制每条线,这样会绘制出很漂亮的颜色
for i in range(3):plot_epipolar_line(im2, F, x2[:, i], e, False)
title(u'outer polar')
axis('off')show()

相关文章:

OpenCV 画极线
from pylab import * import cv2from backend._gs_ import stereo_cameradef compute_epipole(F):""" 从基础矩阵 F 中计算右极点(可以使用 F.T 获得左极点)"""# 返回 F 的零空间(Fx0)U,S,V np.linalg.svd(F)e V[-1]return e/e[2]def plot_epi…...
之md5sum)
Linux命令(109)之md5sum
linux命令之md5sum 1.md5sum介绍 linux命令md5sum是用来计算和校验文件的MD5值。 另外: md5sum是用来校验文件内容,与文件名是否相同无关 md5sum校验文件时,逐位校验,如果文件越大,校验所需时间就越长 2.md5sum用…...
JavaEE入门介绍,HTTP协议介绍,常用状态码及含义,服务器介绍(软件服务器、云服务器)
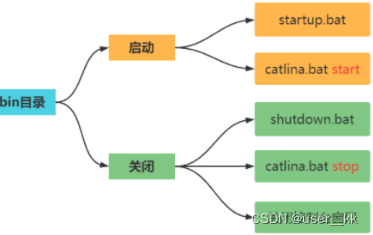
一、JavaEE入门 JavaEE(Java Enterprise Edition),Java企业版,是一个用于企业级web开发(不需要使用控制台)平台。最早由Sun公司定制并发布,后由Oracle负责维护。 JavaEE平台规范了在开发企业级w…...
FPGA时序分析与约束(7)——通过Tcl扩展SDC
一、概述 术语“Synopsys公司设计约束”(又名SDC,Synopsys Design Constraints)用于描述对时序、功率和面积的设计要求,是EDA工具中用于综合、STA和布局布线最常用的格式。本文介绍时序约束的历史概要和SDC的描述。 二、时序约束…...

C++面试——多线程详解
C11提供了语言层面上的多线程,包含在头文件<thread>中。它解决了跨平台的问题,提供了管理线程、保护共享数据、线程间同步操作、原子操作等类。C11 新标准中引入了5个头文件来支持多线程编程,如下图所示: 多进程与多线程 多…...

matlab 布尔莎七参数坐标转换模型
目录 一、算法原理二、代码实现三、结果展示本文由CSDN点云侠原创,原文链接。爬虫自重,把自己当个人。 一、算法原理 算法原理与实现代码已在免费文章:布尔莎七参数坐标转换模型一文中给出,不想看付费文章直接跳转即可。 二、代码实现 clc; clear; close all; %% --...
Android---StartActivity启动过程
在手机桌面应用中点击某一个 icon 之后,最终是通过 startActivity 去打开某一个 Activity 页面。我们知道,Android 中的一个 APP 就相当于一个进程。所以,startActivity 操作中还需要判断,目标 Activity 的进程是否已经创建。如果…...
隐私计算python实现Paillier同态加密
1.基本概念 Paillier同态加密是一种公钥加密方案,具有同态加密的特性。它由Pascal Paillier于1999年提出。 Paillier同态加密基于数论问题,其安全性基于大整数分解问题和离散对数问题的困难性。该方案可以用于保护隐私数据,同时支持在加密状态…...

代码随想录打卡第五十五天|● 300.最长递增子序列 ● 674. 最长连续递增序列 ● 718. 最长重复子数组
300.最长递增子序列 **题目:**给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0…...

C# 创建Oceanbase ODBC数据源 DSN
需要管理员权限打开VS,因为只有管理员权限可以修改注册表 using Microsoft.Win32; using System; using System.Collections.Generic; using System.ComponentModel; using System.Data; using System.Data.Odbc; using System.Diagnostics; using System.Drawing;…...
)
C++ 常用函数汇总#include<algorithm>(3万字总结)
文章目录 1. 排序(Sorting)1.1 sort(first, last):对指定范围内的元素进行升序排序1.2 stable_sort(first, last):在保持相等元素的相对顺序的情况下对指定范围内的元素进行排序1.3 partial_sort(first, middle, last):对范围内的元素进行部分排序,使得前部分是最小的,但…...

Google Archive Patch 基础应用代码记录
项目地址 Google Archive Patch 前置 <!-- 差量应用模块 --> <dependency><groupId>com.google.archivepatcher</groupId><artifactId>archive-patch-applier</artifactId><version>1.0.4</version><scope>test</…...
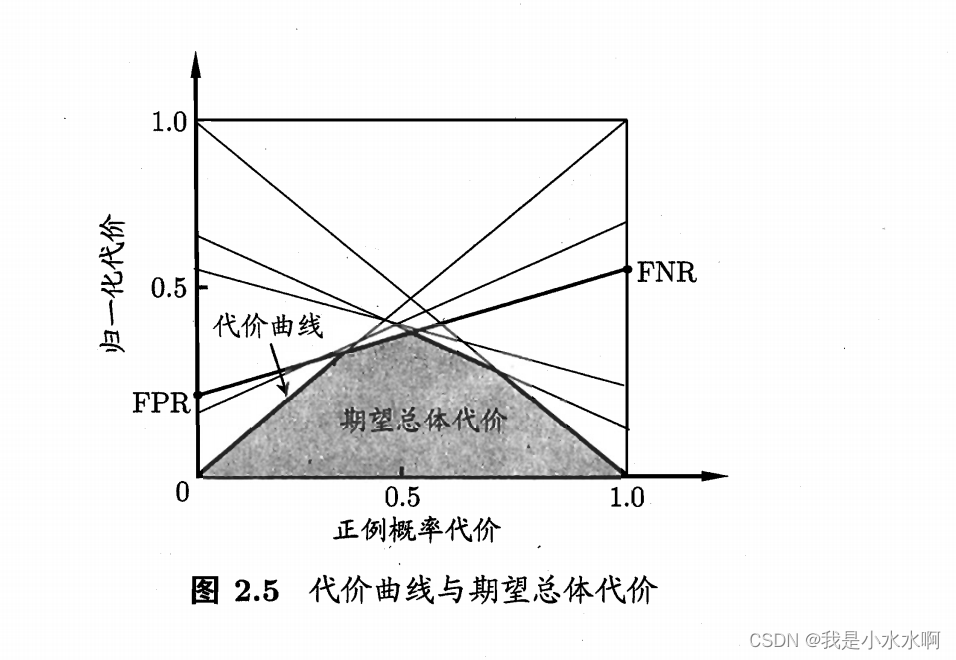
机器学习——代价敏感错误率与代价曲线
文章目录 代价敏感错误率实现代价曲线例子 代价敏感错误率 指在分类问题中,不同类别的错误分类所造成的代价不同。在某些应用场景下,不同类别的错误分类可能会产生不同的代价。例如,在医学诊断中,将疾病患者错误地分类为健康人可…...

如何利用 ChatGPT 提升编程技能
目录 前言代码命名与 ChatGPT设计模式与 ChatGPT代码重构与 ChatGPT代码优化与 ChatGPTChatGPT 的潜在挑战与限制成功案例分析最佳实践与注意事项结语 前言 编程是一项充满创造性和挑战的任务,但也是一个需要花费大量时间和精力的领域。在日益复杂的软件开发环境中…...
是什么意思)
ChatGPT:@EqualsAndHashCode(callSuper = false)是什么意思
ChatGPT:EqualsAndHashCode(callSuper false)是什么意思 EqualsAndHashCode(callSuper false)是什么意思? ChatGPT: EqualsAndHashCode(callSuper false) 是 Java 中的 Lombok 注解,用于自动生成 equals() 和 hashCode() 方法…...

docker部署的mariadb忘记密码
docker 里的 mariadb 数据库密码忘了,如果以前我会选择直接干掉重装,但是数据怎么办? 1 数据量小 就跳过密码登录进去备份出来 2 想办法改掉密码 我直接选择后者,跳过密码,mariadb10.4以后不能直接改密码了ÿ…...
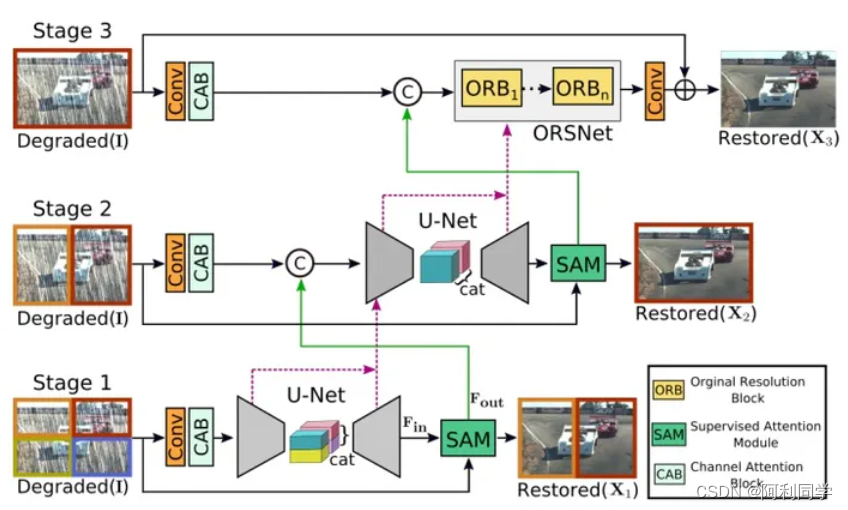
一体化模型图像去雨+图像去噪+图像去模糊(图像处理-图像复原-代码+部署运行教程)
本文主要讲述了一体化模型进行去噪、去雨、去模糊,也就是说,一个模型就可以完成上述三个任务。实现了良好的图像复原功能! 先来看一下美女复原.jpg 具体的: 在图像恢复任务中,需要在恢复图像的过程中保持空间细节…...
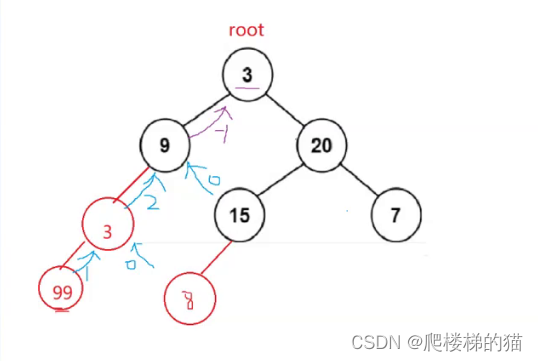
[java/力扣110]平衡二叉树——优化前后的两种方法
分析 根据平衡二叉树的定义,只需要满足:1、根节点两个子树的高度差不超过1;2、左右子树都为平衡二叉树 代码 public class BalancedBinaryTree {public class TreeNode{int val;TreeNode left;TreeNode right;TreeNode(){}TreeNode(int va…...
吉他、班卓琴和贝斯吉他降分器:Arobas Music Guitar 8.1.1
Arobas Music Guitar 是一款专业的吉他、班卓琴和贝斯吉他降分器。在熟练的手中,它不仅可以让您创作,还可以编辑、聆听和录制,以及导入和导出乐谱。如果有人感兴趣的话,录音是在八个轨道上进行的,你可以为每个轨道单独…...
cocos tilemap的setTileGIDAt方法不实时更新
需要取消勾选 Enable Culling。同时代码添加:markForUpdateRenderData函数。 floor.setTileGIDAt(102427,newP.x,newP.y,0); //中心 floor.markForUpdateRenderData(); 具体问题参考官网说明: Cocos Creator 3.2 手册 - 项目设置...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...
