796. 子矩阵的和(二维前缀和)
题目:
796. 子矩阵的和 - AcWing题库

思路:
1.暴力搜索(搜索时间复杂度为O(n2),很多时候会超时)
2. 前缀和(左上角(二维)前缀和):本题特殊在不是直接求前n个数的和,而是求矩阵中某个元素左上角所以数的和(包括该元素自己),利用左上角前缀和的运算求子矩阵和。
3.在求左上角前缀和以及由左上角前缀和求子矩阵的过程中都需要运用到容斥原理!!!
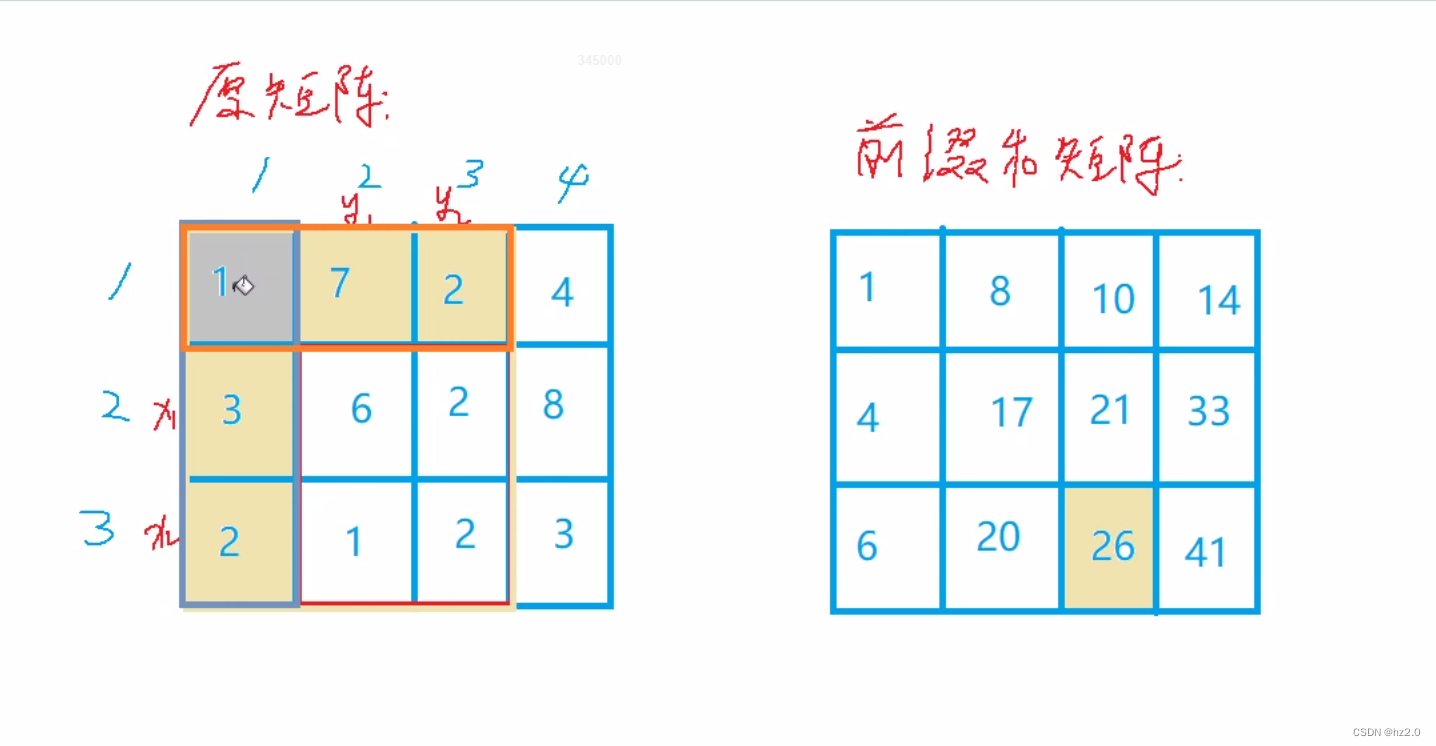
代码:
#include<iostream>
#include<cstdio>
using namespace std;
typedef unsigned long long ull;
const int N = 1010;
int n, m, q;
ull a[N][N], s[N][N];//a存储数据,s存储左上前缀和
int main()
{cin >> n >> m >> q;for (int i = 1; i <= n; i++)//入读数据for (int j = 1; j <= m; j++)scanf("%d", &a[i][j]);for (int i = 1; i <= n; i++)//求左上前缀和for (int j = 1; j <= m; j++)s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];//容斥原理while (q--) {ull x1, y1, x2, y2;scanf("%llu%llu%llu%llu", &x1, &y1, &x2, &y2);printf("%lld\n", s[x2][y2] - s[x2][y1 - 1] - s[x1 - 1][y2] + s[x1 - 1][y1 - 1]);//容斥原理}
}相关文章:

796. 子矩阵的和(二维前缀和)
题目: 796. 子矩阵的和 - AcWing题库 思路: 1.暴力搜索(搜索时间复杂度为O(n2),很多时候会超时) 2. 前缀和(左上角(二维)前缀和):本题特殊在不是直接求前…...
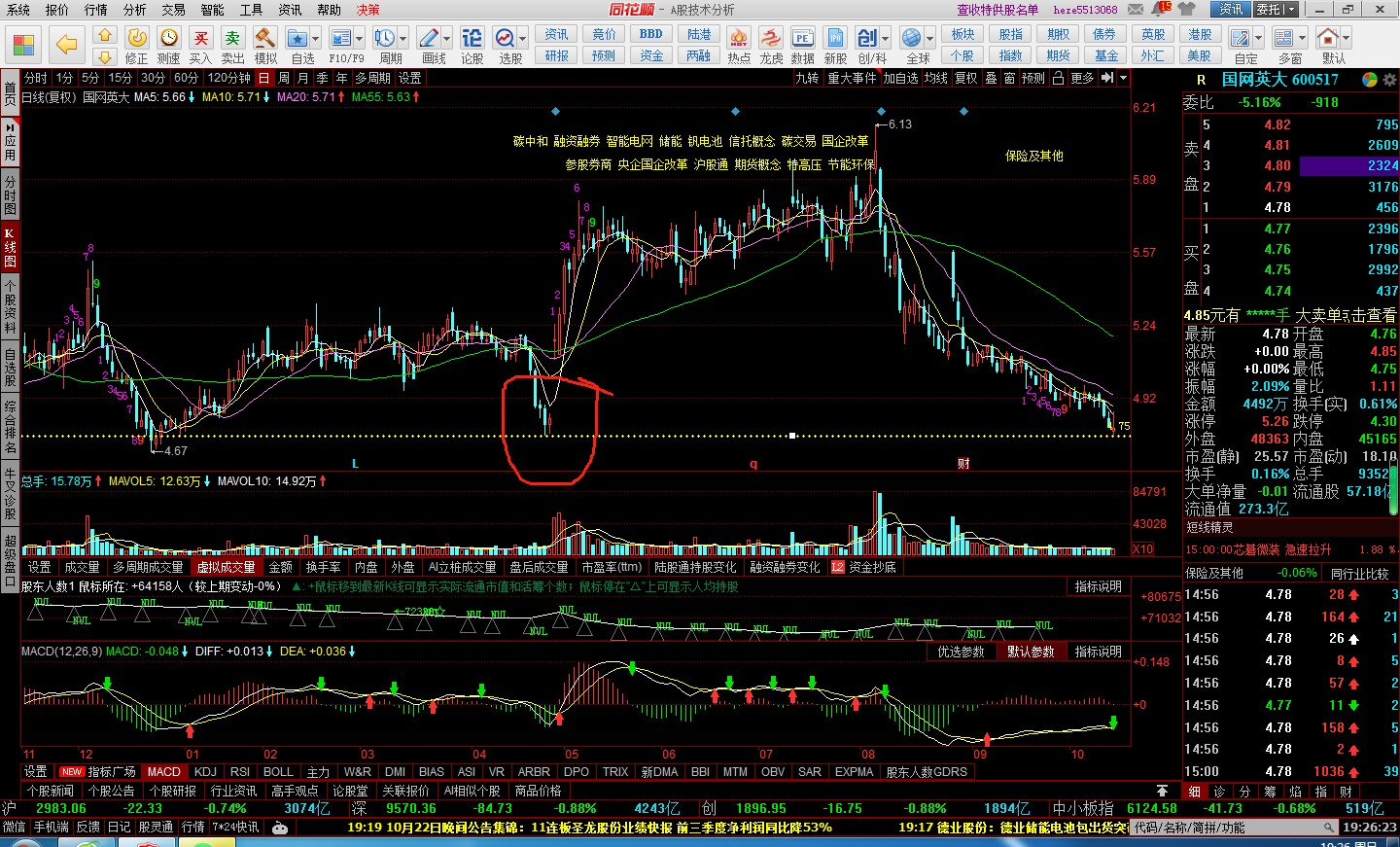
利用ChatGPT进行股票走势分析
文章目录 1. 股票分析2. 技巧分析3. 分析技巧21. 股票分析 这张图片显示了一个股票交易软件的界面。以下是根据图片内容的一些解读: 股票代码: 图片右上角显示的代码是“600517”,这是股票的代码。 图形解读: 该图展示了股票的日K线图。其中,蜡烛图表示每日的开盘、收盘、最…...
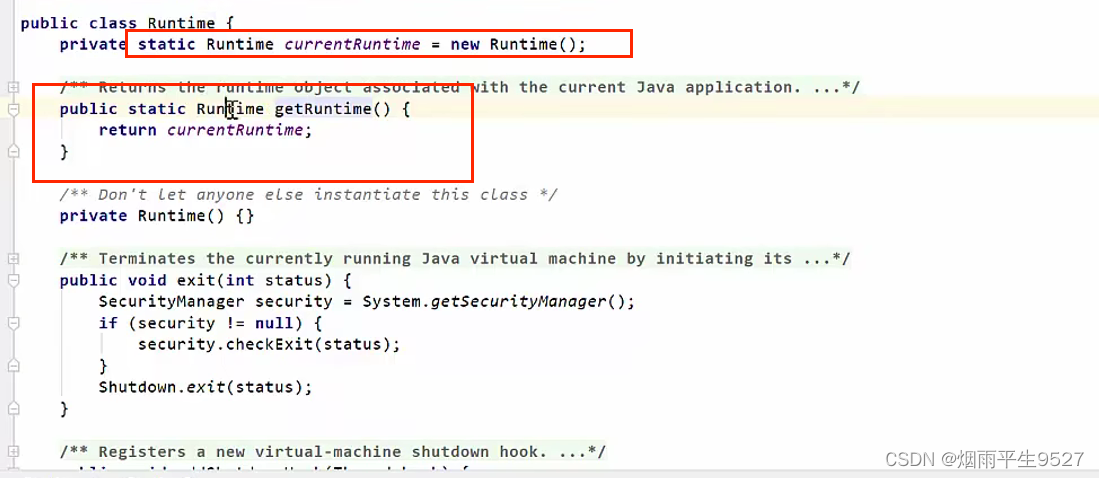
万字解析设计模式之单例模式
一、概述 1.1简介 单例模式(Singleton Pattern)是 Java 中最简单的设计模式之一。这种类型的设计模式属于创建型模式,它提供了一种创建对象的最佳方式。 这种模式涉及到一个单一的类,该类负责创建自己的对象,同时确保…...

vue2.x 二次封装element ui 中的el-dialog
在做后台管理系统的时候,dialog组件是我们使用频率比较高的组件,但是有一些需求现有的组件是不满足的。因此会需要我们做二次封装。 组件本身的属性我们保留,只需要根据需求添加,然后在使用的时候props去拿取使用就可以了。 本次遇…...

ssh连接Ubuntu虚拟机出现connection reset by ip地址 port 22怎么解决
使用前提:我是用Windows去连接安装在本机的Ubuntu虚拟机的时候出现的这个问题。 解决的方法:我使用了很多网络上方法,都没有用,发现我把IP地址搞错了 请继续看下去,因为有可能你会错过解决的方法。 在Windows网络连…...

树莓派4B安装ffmpeg
环境: piraspberrypi:~/x264 $ lsb_release -aNo LSB modules are available.Distributor ID: RaspbianDescription: Raspbian GNU/Linux 10 (buster)Release: 10Codename: buster 装H264 git clone --depth 1 https://code.videolan.org/video…...
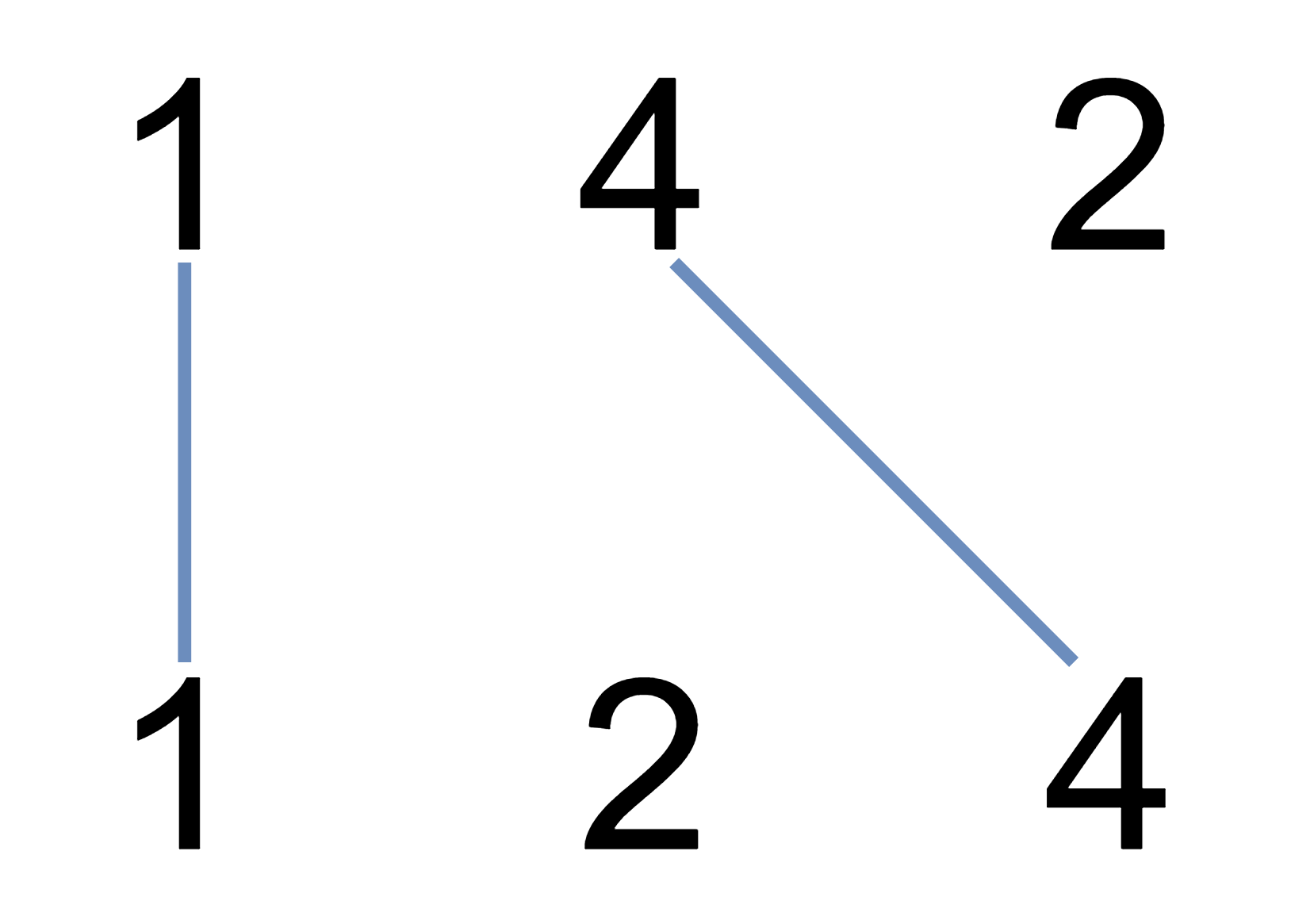
LeetCode|动态规划|1035. 不相交的线 、53. 最大子数组和
目录 一、1035. 不相交的线 1.题目描述 2.解题思路 3.代码实现 二、53. 最大子数组和 1.题目描述 2.解题思路 3.代码实现(动态规划解法) 一、1035. 不相交的线 1.题目描述 在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。 现…...
一体式IO模块:汽车行业的数字化转型助推器
随着市场经济需求的不断增长,汽车行业的自动化和智能化已经成为行业发展的必然趋势。在这个背景下,汽车行业的工作流程变得越来越复杂,工业机器人的广泛应用为汽车生产提供了强有力的支持,它们扮演着装配工、操作工、焊接工等多种…...

OpenCV官方教程中文版 —— Hough 直线变换
OpenCV官方教程中文版 —— Hough 直线变换 前言一、原理二、OpenCV 中的霍夫变换三、Probabilistic Hough Transform 前言 目标 • 理解霍夫变换的概念 • 学习如何在一张图片中检测直线 • 学习函数:cv2.HoughLines(),cv2.HoughLinesP() 一、原理…...
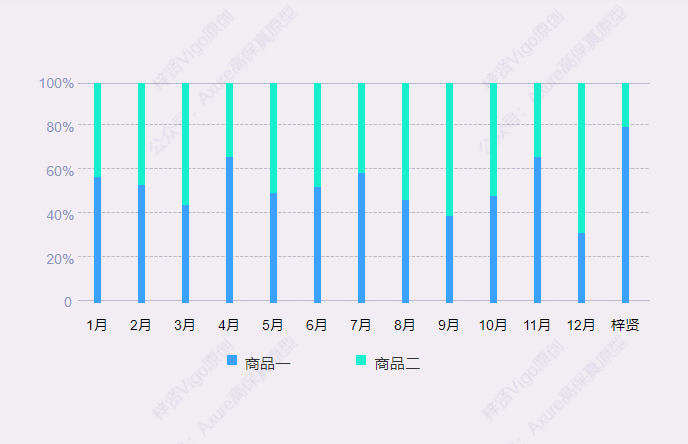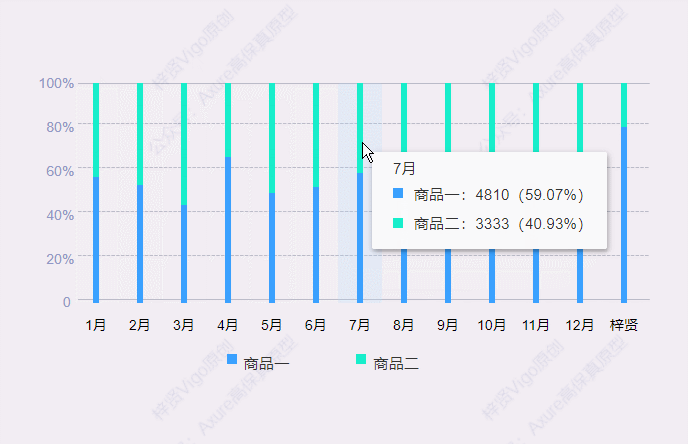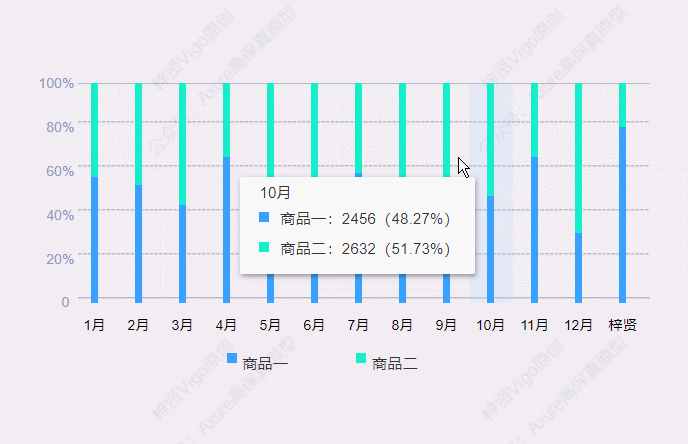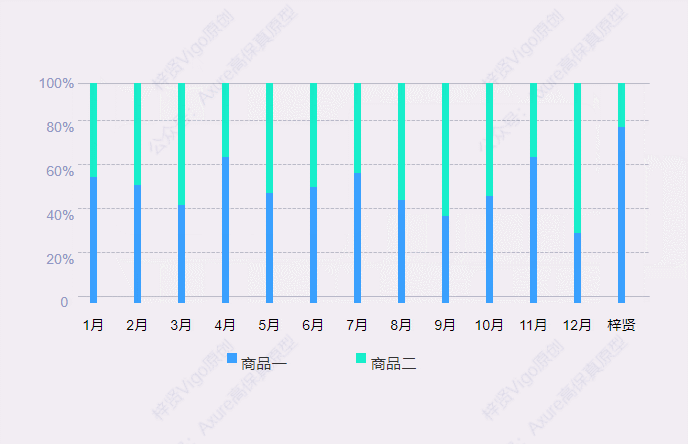
【Axure高保真原型】百分比堆叠柱状图
今天和大家分享百分比堆叠柱状图的的原型模板,鼠标移入堆叠柱状图后,会显示数据弹窗,里面可以查看具体项目对应的数据和占比。那这个原型模板是用中继器制作的,所以使用也很方便,只需要在中继器表格里维护项目数据信息…...

Vue.js中的双向数据绑定(two-way data binding)
聚沙成塔每天进步一点点 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 欢迎来到前端入门之旅!感兴趣的可以订阅本专栏哦!这个专栏是为那些对Web开发感兴趣、刚刚踏入前端领域的朋友们量身打造的。无论你是完全的新手还是有一些基础的开发…...

TFN 2.5G SDH传输分析仪 FT100-D300S
今天给大家带来一款TFN 2.5G SDH传输分析仪--TFN FT100-D300S. D300S SDH测试模块,是FT100智能网络测试平台产品家族的一部分,是一个坚固耐用、锂电池超长供电的传统PDH/SDH测试解决方案,支持2.5Gbps到2.048Mbps速率的传输链路测试。支持在线…...
电脑录像功能在哪?一文帮你轻松破解
“电脑录像功能在哪里呀?最近因工作上的原因,需要使用电脑来录像,但是找了一上午都找不到在哪里,眼看已经快没时间了,现在真的很急,希望大家帮帮我。” 电脑已经成为了人们生活和工作中必不可少的工具&…...

基于长短期神经网络的可上调容量PUP预测,基于长短期神经网络的可下调容量PDO预测,LSTM可调容量预测
目录 背影 摘要 代码和数据下载:基于长短期神经网络的可上调容量PUP预测,基于长短期神经网络的可下调容量PDO预测,LSTM可调容量预测(代码完整,数据齐全)资源-CSDN文库 https://download.csdn.net/download/abc991835105/88230834 LSTM的基本定义 LSTM实现的步骤 基于长短…...

站群服务器有哪些优势?
站群服务器有哪些优势? 站群服务器是单独为一个网站或者多个网站配置独立IP的一种服务器。企业或是用户如果想组建多个网站的话就需要用站群服务器了。 站群服务器可以提高搜索引擎多个网站的关注度,提高网站文章的收录以及网站文章的访问量。站群服务器有哪些优势…...

故障诊断模型 | Maltab实现LSTM长短期记忆神经网络故障诊断
文章目录 效果一览文章概述模型描述源码设计参考资料效果一览 文章概述 故障诊断模型 | Maltab实现LSTM长短期记忆神经网络故障诊断 模型描述 长短记忆神经网络——通常称作LSTM,是一种特殊的RNN,能够学习长的依赖关系。 他们由Hochreiter&Schmidhuber引入,并被许多人进行了…...

【WSL 2】Windows10 安装 WSL 2,并配合 Windows Terminal 和 VSCode 使用
【WSL 2】Windows10 安装 WSL 2,并配合 Windows Terminal 和 VSCode 使用 1 安装 Windows Terminal2 安装 WSL 23 在 Windows 文件资源管理器中打开 WSL 项目4 在 VSCode 中使用 WSL 24.1 必要准备4.2 从 VSCode 中 Connect WSL4.3 从 Linux 中打开 VSCode 1 安装 W…...
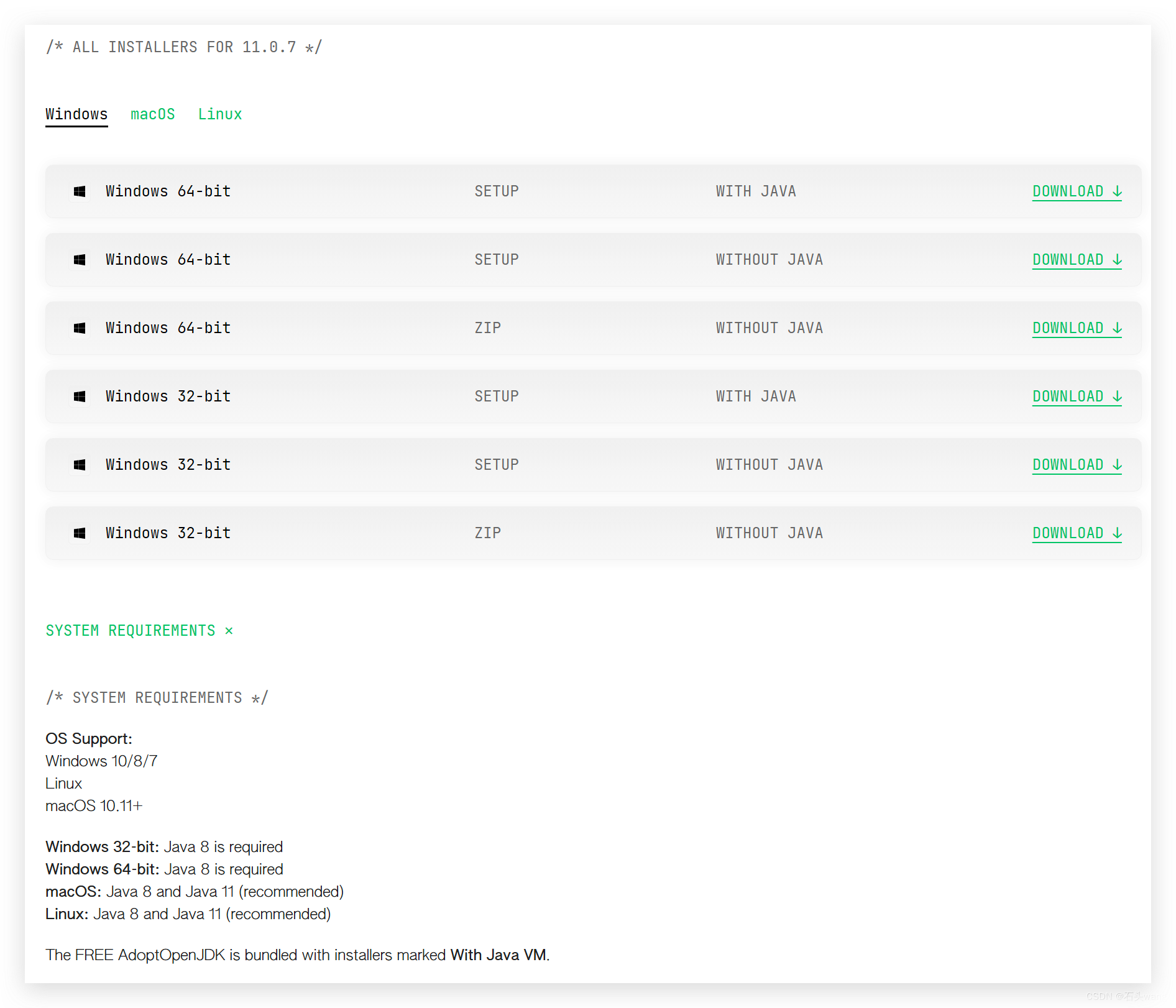
DbVisualizer和DBeaver启动不来,启动报错
启动报错 大多数启动报错都是因为你没有用管理员身份运行程序,提示的错误都是八竿子打不着的什么jdk、jvm问题。 比如DbVisualizer提示什么jvm配置参数,实际dbvis.exe 用管理员身份打开即可(右键 dbvis.exe->属性->兼容性->勾上 “…...
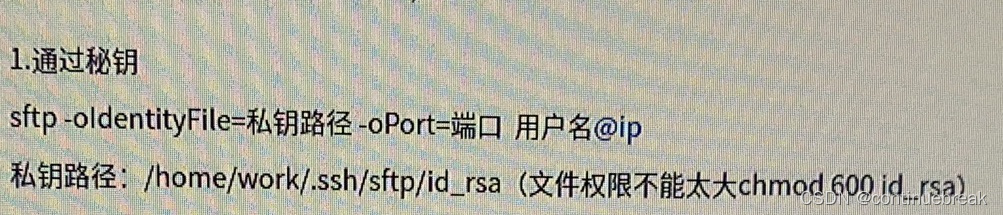
sftp连接远程服务器命令
...

el-select 、el-option 常见用法
<template> <div> // 可以多选 // 添加小叉,点击清空选择器 <el-select v-model"selectedValue" multiple disabled clearable filterable > <el-option …...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...
