【python数学建模】特征值与特征向量运用
1、求数列通项
(1)转化为求矩阵的幂次问题
例:求斐波那契数列的通项公式
已知斐波那契数列满足: F k + 2 = F k + 1 + F k F_{k+2}=F_{k+1}+F_{k} Fk+2=Fk+1+Fk
(a) 降阶:将二阶差分方程转化为一阶差分方程组
{ F k + 1 = F k + 1 F k + 2 = F k + 1 + F k \begin{cases} F_{k+1}=F_{k+1}\\ F_{k+2}=F_{k+1}+F_{k} \end{cases} {Fk+1=Fk+1Fk+2=Fk+1+Fk 写成矩阵形式: a k + 1 = A a k k = 0 , 1 , 2 , . . . a_{k+1}=Aa_{k}\ k=0,1,2,... ak+1=Aak k=0,1,2,...
其中 A = ( 0 1 1 1 ) , a k = ( F k F k + 1 ) , a 0 = ( 1 1 ) A=\left(\begin{matrix} 0&1\\1&1 \end{matrix}\right)\ , \ a_k=\left(\begin{matrix} F_k\\F_{k+1} \end{matrix}\right)\ , \ a_0=\left(\begin{matrix} 1\\1 \end{matrix}\right) A=(0111) , ak=(FkFk+1) , a0=(11)
推导得有: a k = A k a 0 a_k=A^ka_0 ak=Aka0
(b) 求矩阵的Jordan标准形
矩阵的特征方程为: λ 2 − λ − 1 \lambda^2-\lambda-1 λ2−λ−1,特征根为 1 ± 5 2 \frac{1\pm \sqrt5}{2} 21±5,特征向量为 , ( 1 ± 5 2 1 ) \ , \ \left(\begin{matrix} \frac{1\pm \sqrt5}{2}\\1 \end{matrix}\right) , (21±51),取特征向量为列向量构成矩阵 P P P
则有 A = P ( 1 + 5 2 0 0 1 − 5 2 ) P − 1 A=P\left(\begin{matrix} \frac{1+ \sqrt5}{2}&0\\0&\frac{1- \sqrt5}{2} \end{matrix}\right)P^{-1} A=P(21+50021−5)P−1
从而 a k = A k a 0 a_k=A^ka_0 ak=Aka0,斐波那契数列的通项公式为 a k a_k ak的第一行元素。
(c) python实现
import sympy as sp
sp.var('k',positive=True,integre=True)
a=sp.Matrix([[0,1],[1,1]])
val=a.eigenvals()
vec=a.eigenvects()
P,D=a.diagonalize()
ak=P@(D**k)@(P.inv())
F=ak@sp.Matrix([1,1])
print(sp.latex(sp.simplify(F[0])))
求出通项公式为: F k = 2 − k ( 2 ( 1 − 5 ) k + 5 ( 1 + 5 ) k + 3 ( 1 + 5 ) k ) 5 + 5 F^k=\frac{2^{- k} \left(2 \left(1 - \sqrt{5}\right)^{k} + \sqrt{5} \left(1 + \sqrt{5}\right)^{k} + 3 \left(1 + \sqrt{5}\right)^{k}\right)}{\sqrt{5} + 5} Fk=5+52−k(2(1−5)k+5(1+5)k+3(1+5)k)
取值:
f = sp.lambdify(k,F[0])
print(f(9))
(2)特征根法求通项
由于斐波那契数列的特征根是互异的,故可设通项为:
F k = c 1 ( 1 + 5 2 ) k + c 2 ( 1 − 5 2 ) k F_k=c_1(\frac{1+\sqrt5}{2})^k+c_2(\frac{1-\sqrt5}{2})^k Fk=c1(21+5)k+c2(21−5)k
代入初值条件求解上述二元一次方程: F 0 = F 1 = 1 F_0=F_1=1 F0=F1=1
{ c 1 + c 2 = 1 c 1 ( 1 + 5 2 ) + c 2 ( 1 − 5 2 ) = 1 \begin{cases} c_1+c_2=1\\ c_1(\frac{1+\sqrt5}{2})+c_2(\frac{1-\sqrt5}{2})=1 \end{cases} {c1+c2=1c1(21+5)+c2(21−5)=1
解得 { c 1 = 1 2 + 5 10 c 2 = 1 2 − 5 10 \begin{cases} c1=\frac{1}{2}+\frac{\sqrt5}{10}\\c2=\frac{1}{2}-\frac{\sqrt5}{10} \end{cases} {c1=21+105c2=21−105,从而得到通项公式。
python实现:
import sympy as sp
x=sp.symbols('x')
c=sp.symbols('c:2')
f=sp.Eq(x**2,x+1)
vals=list(sp.solveset(f))
eq1=c[0]+c[1]-1
eq2=c[0]*vals[0]+c[1]*vals[1]-1
s=sp.solve([eq1,eq2])
(3)利用rsolve函数求解有理系数单变量递推式
import sympy as sp
k=sp.symbols('k')
y=sp.Function('y')
f=y(k+2)-y(k+1)-y(k)
F=sp.rsolve(f,y(k),{y(0):1, y(1):1})
2、Leslie种群模型
3、Pagerank算法
相关文章:

【python数学建模】特征值与特征向量运用
1、求数列通项 (1)转化为求矩阵的幂次问题 例:求斐波那契数列的通项公式 已知斐波那契数列满足: F k 2 F k 1 F k F_{k2}F_{k1}F_{k} Fk2Fk1Fk (a) 降阶:将二阶差分方程转化为一阶…...

什么是 CNN? 卷积神经网络? 怎么用 CNN 进行分类?(1)
先看卷积是啥,url: https://www.bilibili.com/video/BV1JX4y1K7Dr/?spm_id_from333.337.search-card.all.click&vd_source7a1a0bc74158c6993c7355c5490fc600 下面这个式子就是卷积 看完了,感觉似懂非懂 下一个参考视频:https://www.y…...

java解决修改图片尺寸,压缩图片后出现背景变黑,图片字体模糊问题
将以下数学公式的图片使用Hutool提供的图片工具类改变尺寸 代码如下: package com.jason.common.file.word;import cn.hutool.core.img.ImgUtil; import cn.hutool.core.io.FileUtil;import javax.imageio.ImageIO; import java.awt.*; import java.awt.image.BufferedImage;…...

jq/js检测鼠标指针移动离开页面
通过 mouseout 鼠标事件,判断鼠标去往哪个元素 知识点:relatedTarget 事件属性 定义和用法 relatedTarget 事件属性返回与事件的目标节点相关的节点。 对于 mouseover 事件来说,该属性是鼠标指针移到目标节点上时所离开的那个节点。 对于 …...

ICC2: 如何在显示GUI操作产生的命令
我正在「拾陆楼」和朋友们讨论有趣的话题,你⼀起来吧? 拾陆楼知识星球入口 ICC2:自定义快捷键和菜单 VIEW -> Perference -> Global Settings 把display commands in logging console 下面几个都勾上即可。...
内网渗透——macOS上搭建Web服务器
# 公网访问macOS本地web服务器【内网穿透】 文章目录 1. 启动Apache服务器2. 公网访问本地web服务2.1 本地安装配置cpolar2.2 创建隧道2.3 测试访问公网地址3. 配置固定二级子域名3.1 保留一个二级子域名3.2 配置二级子域名4. 测试访问公网固定二级子域名 以macOS自带的Apache…...
Centos下用nodejs实现一个简单的web服务器
WebRTC是音视频直播中最常用的一个框架,在使用的过程中,我们就需要实现一个服务器端。本文以nodejs实现一个服务器为例,讲述一下在centos下如何用nodejs实现一个简单的web服务器。 一、安装nodejs 在linux环境下安装nodejs有多重方式&#x…...

3.10每日一题(三角有理函数积分(三角函数加减乘除))
1、通过类型判别方法>判断出为凑 tanx 2、加项减项拆常用的积分公式 注:tanx的导数是:cosx的平方分之一 cosx的平方分之一 1 tanx arctanx的求导公式要记住...
python练习(猜数字,99乘法表)
python练习(猜数字,99乘法表) 猜数字 import random num1random.choice(range(1,101))for i in range(11):num2input("plz input a number:")num2int(num2)if num1<num2:print("太大了,小一点")elif num1>num2:print("…...

正确部署Baichuan2(Ubuntu20.4) 步骤及可能出现的问题
部署其实是不太复杂的,但实际上也耗费了接近2-3天的时间去不断的设置 1 硬件配置信息 采用esxi 虚拟化的方式将T4 卡穿透给esxi 种的ubuntu20.4虚拟机 CPU给到8 core 内存至少32GB以上 T4卡是16GB 2 预先准备OS环境 这里使用的是ubuntu20.4版本,esxi中需要设置uefI启动方…...

docker 部署prometheus和grafana
1.启动node 容器 docker run -d -p 9100:9100 -v "/proc:/host/proc:ro" -v "/sys:/host/sys:ro" -v "/:/rootfs:ro" --net"bridge" prom/node-exporter 2.访问http://192.168.1.122:9100/metrics 3.创建文件/home/prometheus/ 下…...
在本地模拟C/S,Socket套接字的使用
public class SocketTCP01Server {public static void main(String[] args) throws IOException {/**1.在本机的 9999 端口监听 ,等待连接细节: 要求在本机没有其他服务在监听999细节:这个ServerSocket 可以通过accept()返回多个Socket[多个客…...
)
香港科技大学广州|可持续能源与环境学域博士招生宣讲会—东南大学专场!!!(暨全额奖学金政策)
香港科技大学广州|可持续能源与环境学域博士招生宣讲会—东南大学专场!!!(暨全额奖学金政策) “面向未来改变游戏规则的——可持续能源与环境学域” 专注于能源环境跨学科尖端技术研究 培养可持续能源技术…...

[Leetcode] 0108. 将有序数组转换为二叉搜索树
108. 将有序数组转换为二叉搜索树 题目描述 给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 高度平衡 二叉搜索树。 高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。 示例 1:…...

Pandas数据导入和导出:CSV、Excel、MySQL、JSON
导入MySQL查询结果:read_sql import pandascon "mysqlpymysql://user:pass127.0.0.1/test" sql "SELECT * FROM student WHERE id 2"# sql查询 df1 pandas.read_sql(sqlsql, concon) print(df1)导入MySQL整张表:read_sql_table…...

第16期 | GPTSecurity周报
GPTSecurity是一个涵盖了前沿学术研究和实践经验分享的社区,集成了生成预训练 Transformer(GPT)、人工智能生成内容(AIGC)以及大型语言模型(LLM)等安全领域应用的知识。在这里,您可以…...
省钱兄短剧短视频视频滑动播放模块源码支持微信小程序h5安卓IOS
# 开源说明 开源省钱兄短剧系统的播放视频模块(写了测试弄了好久才弄出来、最核心的模块、已经实战了),使用uniapp技术,提供学习使用,支持IOSAndroidH5微信小程序,使用Hbuilder导入即可运行 #注意ÿ…...
SDRAM学习笔记(MT48LC16M16A2,w9812g6kh)
一、基本知识 SDRAM : 即同步动态随机存储器(Synchronous Dynamic Random Access Memory), 同步是指其时钟频率与对应控制器(CPU/FPGA)的系统时钟频率相同,并且内部命令 的发送与数据传输都是以该时钟为基准ÿ…...
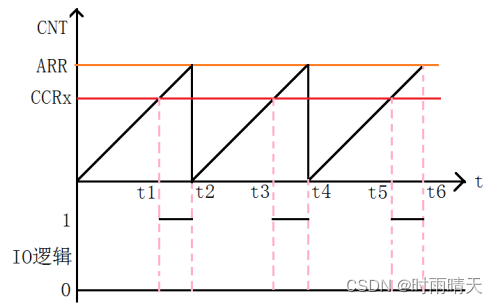
ARM 学习笔记3 STM32G4 定时器相关资料整理
官方文档 AN4539 HRTIM cookbookAN4539_HRTIM使用指南 中文版的文档,注意文档的版本号滞后于英文原版ST MCU中文文档 中文文档汇总 博客文章 STM32-定时器详解【STM32H7教程】第63章 STM32H7的高分辨率定时器HRTIM基础知识和HAL库APIstm32f334 HRTIM触发ADC注入中…...

LeetCode 917 仅仅反转字母 简单
题目 - 点击直达 1. XXXXX1. 917 仅仅反转字母 简单1. 原题链接2. 题目要求3. 基础框架 2. 解题思路1. 思路分析2. 时间复杂度3. 代码实现 1. XXXXX 1. 917 仅仅反转字母 简单 给你一个字符串 s ,根据下述规则反转字符串: 所有非英文字母保留在原有位置…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...

Matlab实现任意伪彩色图像可视化显示
Matlab实现任意伪彩色图像可视化显示 1、灰度原始图像2、RGB彩色原始图像 在科研研究中,如何展示好看的实验结果图像非常重要!!! 1、灰度原始图像 灰度图像每个像素点只有一个数值,代表该点的亮度(或…...
