当前位置： 首页 > news >正文

ARM 学习笔记3 STM32G4 定时器相关资料整理

news 2026/2/9 14:48:31

官方文档

  1. AN4539 HRTIM cookbook
  2. AN4539_HRTIM使用指南 中文版的文档，注意文档的版本号滞后于英文原版
  3. ST MCU中文文档 中文文档汇总

博客文章

  1. STM32-定时器详解
  2. 【STM32H7教程】第63章 STM32H7的高分辨率定时器HRTIM基础知识和HAL库API
  3. stm32f334 HRTIM触发ADC注入中断采样
  4. 电机控制基础1——定时器基础知识与PWM输出原理 此文定时器分类图很直观
  5. stm32影子寄存器、预装载寄存器，TIM_OC1PreloadConfig和TIM_ARRPreloadConfig的作用
  6. 利用STM32的TIM1/TIM8输出可以移相的互补PWM
  7. STM32定时器三种中心对齐计数模式简介
  8. STM32F103高级定时器死区时间的计算
  9. 高级定时器实例-PWM互补输出与刹车功能 好文章

Tips

PWM模式1 与 PWM模式2

个人速记：

  • PWM模式1，不论增减计数，cnt低于ccr为有效电平，高于则为无效电平。
  • PWM模式2，不论增减计数，cnt高于ccr为有效电平，低于则为无效电平。

以下摘自 分享：PWM输出极性高低的区别
在这里插入图片描述

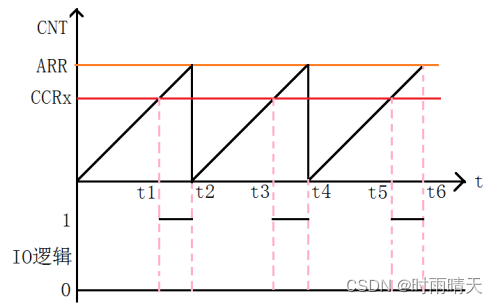
110：PWM模式1－ 在向上计数时，一旦TIMx_CNT<TIMx_CCR1时通道1为有效电平，否则为
无效电平；在向下计数时，一旦TIMx_CNT>TIMx_CCR1时通道1为无效电平(OC1REF=0)，否
则为有效电平(OC1REF=1)。
111：PWM模式2－ 在向上计数时，一旦TIMx_CNT<TIMx_CCR1时通道1为无效电平，否则为
有效电平；在向下计数时，一旦TIMx_CNT>TIMx_CCR1时通道1为有效电平，否则为无效电
平

其他

  1. Auto-reload preload enable， 控制TIMx_ARR寄存器是否缓冲，为0不缓冲，为1缓冲。类似于TI-DSP中的是否使用CMPA的影子寄存器。

相关文章：

ARM 学习笔记3 STM32G4 定时器相关资料整理

官方文档 AN4539 HRTIM cookbookAN4539_HRTIM使用指南 中文版的文档&#xff0c;注意文档的版本号滞后于英文原版ST MCU中文文档 中文文档汇总 博客文章 STM32-定时器详解【STM32H7教程】第63章 STM32H7的高分辨率定时器HRTIM基础知识和HAL库APIstm32f334 HRTIM触发ADC注入中…...

编程日记 2023/10/31 11:49:05

LeetCode 917 仅仅反转字母 简单

题目 - 点击直达 1. XXXXX1. 917 仅仅反转字母 简单1. 原题链接2. 题目要求3. 基础框架 2. 解题思路1. 思路分析2. 时间复杂度3. 代码实现 1. XXXXX 1. 917 仅仅反转字母 简单 给你一个字符串 s &#xff0c;根据下述规则反转字符串&#xff1a; 所有非英文字母保留在原有位置…...

编程日记 2023/10/31 11:48:03

JAVA深化篇_25—— IO流章节全网最全总结（附详细思维导图）

IO流章节全网最全总结&#xff08;附详细思维导图&#xff09; 本篇开始&#xff0c;先奉上思维导图&#xff1a;&#xff08;下载下来为超高清图&#xff0c;不愁小伙伴看不清&#xff01;&#xff09; 按流的方向分类&#xff1a; 输入流&#xff1a;数据源到程序(InputStr…...

编程日记 2023/10/31 11:47:02

易基因：ChIP-seq等揭示BRWD3调控KDM5活性以维持H3K4甲基化水平的表观机制｜PNAS

大家好&#xff0c;这里是专注表观组学十余年&#xff0c;领跑多组学科研服务的易基因。 组蛋白修饰对调控染色质结构和基因表达至关重要&#xff0c;组蛋白修饰失调可能导致疾病状态和癌症。染色质结合蛋白BRWD3&#xff08;Bromodomain and WD repeat-containing protein 3&…...

编程日记 2023/10/31 11:46:01

C++深度优先(DFS)算法的应用：收集所有金币可获得的最大积分

涉及知识点 深度优化(DFS) 记忆化 题目 节点 0 处现有一棵由 n 个节点组成的无向树&#xff0c;节点编号从 0 到 n - 1 。给你一个长度为 n - 1 的二维 整数 数组 edges &#xff0c;其中 edges[i] [ai, bi] 表示在树上的节点 ai 和 bi 之间存在一条边。另给你一个下标从 0…...

编程日记 2023/10/31 11:44:59

uniapp中APP端使用echarts用formatter设置y轴保留2位小数点不生效

uniapp使用echarts&#xff0c;在内置浏览器中&#xff0c;设置保留2位小数能正常显示&#xff08;代码如下&#xff09;&#xff0c;但是在APP端这个设置不起作用。 yAxis: {type: value,axisLabel: {formatter: function (val) {return val.toFixed(2); //y轴始终保留小数点…...

编程日记 2023/10/31 11:42:58

无糖茶饮三十年，从无人问津到人手一瓶

【潮汐商业评论/原创】 Joan又在外卖上点了一堆瓶装茶饮&#xff0c;东方树叶、燃茶、三得利乌龙茶……买了四五种纯茶&#xff0c;用她的话说&#xff0c;和美式咖啡相比&#xff0c;这些无糖茶更适合他这个中国体质。 事实上&#xff0c;越来越多的消费者开始像Joan一样&am…...

编程日记 2023/10/31 11:41:56

面向Three.js开发者的3D自动纹理化开发包

DreamTexture.js 是面向 three.js 开发者的 3D 模型纹理自动生成与设置开发包&#xff0c;可以为 webGL 应用增加 3D 模型的快速自动纹理化能力。 图一为原始模型, 图二图三为贴图后的模型。提示词&#xff1a; city, Realistic , cinematic , Front view ,Game scene graph 1、…...

编程日记 2023/10/31 11:40:55

数字孪生技术与VR：创造数字未来

在当今数字化浪潮中&#xff0c;数字孪生和虚拟现实&#xff08;VR&#xff09;技术是两大亮点&#xff0c;它们以独特的方式相互结合&#xff0c;为各个领域带来了创新和无限可能。本篇文章将探讨数字孪生与VR之间的关系&#xff0c;以及它们如何共同开辟未来的新前景。 数字…...

编程日记 2023/10/31 11:39:54

系统架构设计师-第15章-面向服务架构设计理论与实践-软考学习笔记

面向服务的体系结构&#xff08;Service-Oriented Architecture, SOA) 面向服务的体系结构&#xff08;Service-Oriented Architecture, SOA&#xff09;是一种软件架构模式&#xff0c;它将应用程序的不同功能组织为一组可重用的、松耦合的、自治的服务&#xff0c;这些服务通…...

编程日记 2023/10/31 11:38:53

为什么我觉得Rust比C++复杂得多？

为什么我觉得Rust比C复杂得多&#xff1f; Rust自学确实有一定门槛&#xff0c;很多具体问题解决起来搜索引擎也不太帮的上忙&#xff0c;会出现卡住的情况&#xff0c;卡的时间长了就放弃了。最近很多小伙伴找我&#xff0c;说想要一些c语言资料&#xff0c;然后我根据自己从…...

编程日记 2023/10/31 11:37:51

python sqlalchemy（ORM）- 03 增删改查

文章目录 ORM更新数据ORM查询ORM删除操作处理关系对象多表的关联查询 本节所有案例基于&#xff08;第一节 python sqlalchemy&#xff08;ORM&#xff09;- 01 ORM简单使用&#xff09;中的User、Address两个模型类 ORM更新数据 查询到模型类对象&#xff0c;直接修改其属性…...

编程日记 2023/10/31 11:36:50

Flutter笔记：完全基于Flutter绘图技术绘制一个精美的Dash图标（上）

Flutter笔记 完全基于Flutter绘图技术绘制一个精美的Dart语言吉祥物Dash&#xff08;上&#xff09; 作者&#xff1a;李俊才 &#xff08;jcLee95&#xff09;&#xff1a;https://blog.csdn.net/qq_28550263 邮箱 &#xff1a;291148484163.com 本文地址&#xff1a;https://…...

编程日记 2023/10/31 11:35:49

学习gorm：彻底弄懂Find、Take、First和Last函数的区别

在gorm中&#xff0c;要想从数据库中查找数据有多种方法&#xff0c;可以通过Find、Take和First来查找。但它们之间又有一些不同。本文就详细介绍下他们之间的不同。 一、准备工作 首先我们有一个m_tests表&#xff0c;其中id字段是自增的主键&#xff0c;同时该表里有3条数据…...

编程日记 2023/10/31 11:33:47

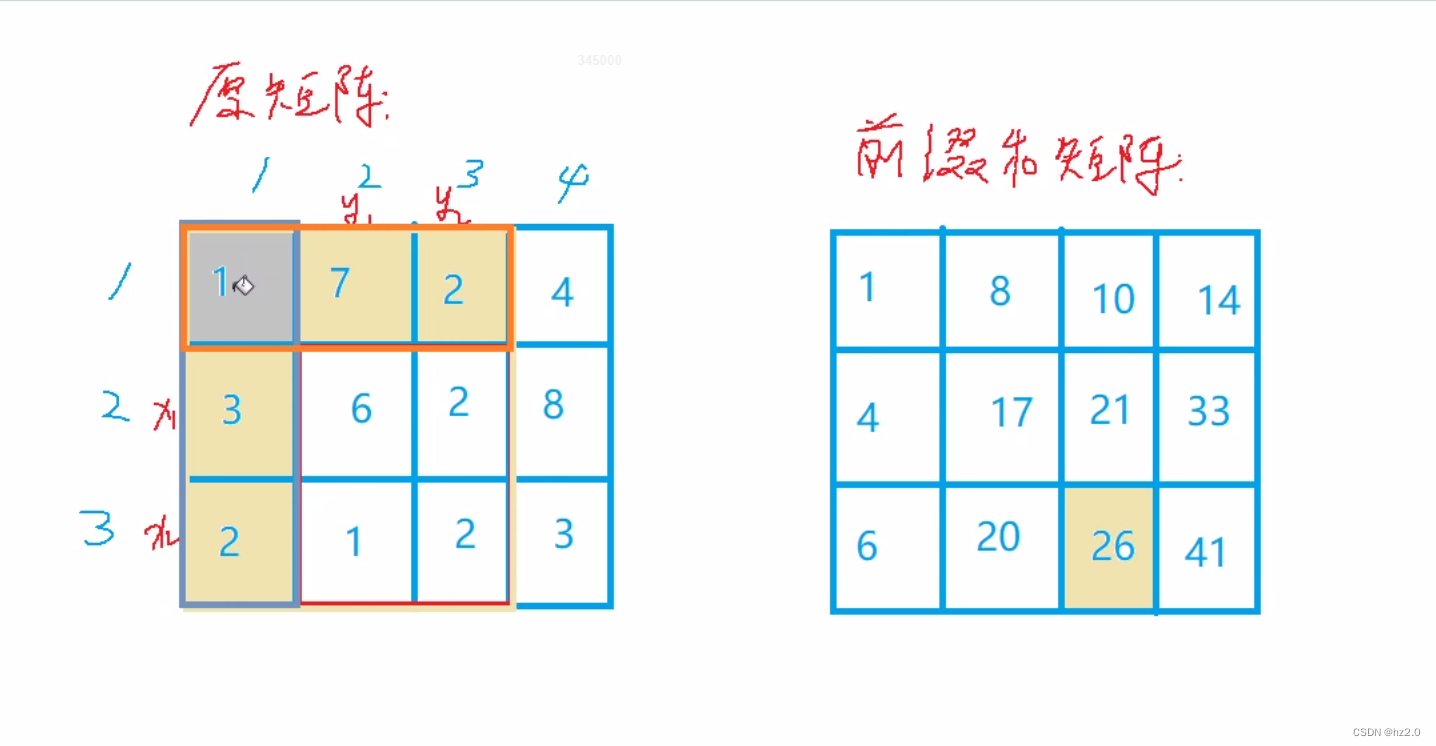
796. 子矩阵的和（二维前缀和）

题目&#xff1a; 796. 子矩阵的和 - AcWing题库 思路&#xff1a; 1.暴力搜索&#xff08;搜索时间复杂度为O(n2)&#xff0c;很多时候会超时&#xff09; 2. 前缀和&#xff08;左上角&#xff08;二维&#xff09;前缀和&#xff09;&#xff1a;本题特殊在不是直接求前…...

编程日记 2023/10/31 11:30:43

利用ChatGPT进行股票走势分析

文章目录 1. 股票分析2. 技巧分析3. 分析技巧21. 股票分析 这张图片显示了一个股票交易软件的界面。以下是根据图片内容的一些解读： 股票代码: 图片右上角显示的代码是“600517”，这是股票的代码。 图形解读: 该图展示了股票的日K线图。其中，蜡烛图表示每日的开盘、收盘、最…...

编程日记 2023/10/31 11:29:40

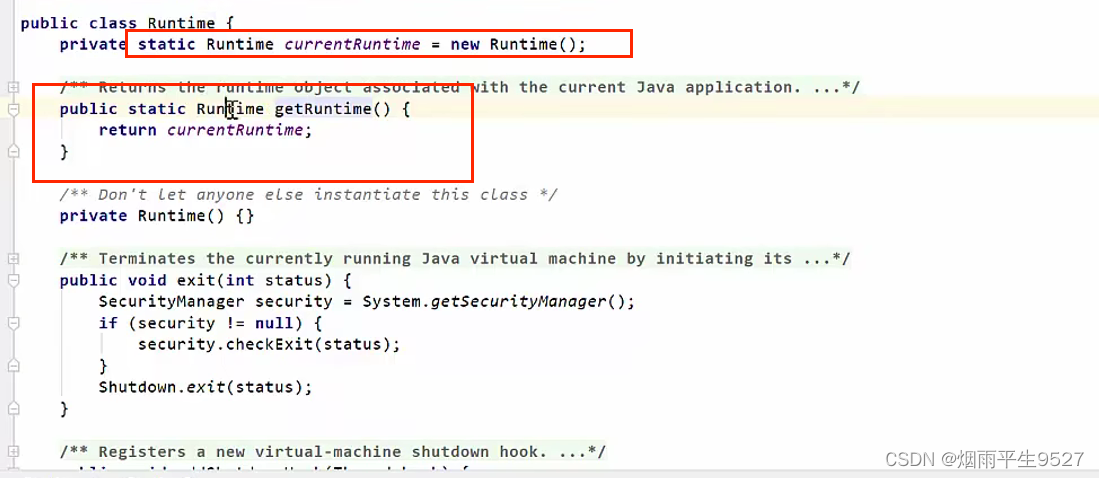
万字解析设计模式之单例模式

一、概述 1.1简介 单例模式&#xff08;Singleton Pattern&#xff09;是 Java 中最简单的设计模式之一。这种类型的设计模式属于创建型模式&#xff0c;它提供了一种创建对象的最佳方式。 这种模式涉及到一个单一的类&#xff0c;该类负责创建自己的对象&#xff0c;同时确保…...

编程日记 2023/10/31 11:28:38

vue2.x 二次封装element ui 中的el-dialog

在做后台管理系统的时候&#xff0c;dialog组件是我们使用频率比较高的组件&#xff0c;但是有一些需求现有的组件是不满足的。因此会需要我们做二次封装。 组件本身的属性我们保留&#xff0c;只需要根据需求添加&#xff0c;然后在使用的时候props去拿取使用就可以了。 本次遇…...

编程日记 2023/10/31 11:27:37

ssh连接Ubuntu虚拟机出现connection reset by ip地址 port 22怎么解决

使用前提&#xff1a;我是用Windows去连接安装在本机的Ubuntu虚拟机的时候出现的这个问题。 解决的方法&#xff1a;我使用了很多网络上方法&#xff0c;都没有用&#xff0c;发现我把IP地址搞错了 请继续看下去&#xff0c;因为有可能你会错过解决的方法。 在Windows网络连…...

编程日记 2023/10/31 11:26:36

树莓派4B安装ffmpeg

环境&#xff1a; piraspberrypi:~/x264 $ lsb_release -aNo LSB modules are available.Distributor ID: RaspbianDescription: Raspbian GNU/Linux 10 (buster)Release: 10Codename: buster 装H264 git clone --depth 1 https://code.videolan.org/video…...

编程日记 2023/10/31 11:25:35

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型

CVPR 2025 | MIMO&#xff1a;支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题&#xff1a;MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者&#xff1a;Yanyuan Chen, Dexuan Xu, Yu Hu…...

编程新知 2025/10/6 14:17:21

ubuntu搭建nfs服务centos挂载访问

在Ubuntu上设置NFS服务器 在Ubuntu上&#xff0c;你可以使用apt包管理器来安装NFS服务器。打开终端并运行&#xff1a; sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享&#xff0c;例如/shared&#xff1a; sudo mkdir /shared sud…...

编程新知 2026/2/6 23:18:59

Java 8 Stream API 入门到实践详解

一、告别 for 循环&#xff01; 传统痛点&#xff1a; Java 8 之前&#xff0c;集合操作离不开冗长的 for 循环和匿名类。例如&#xff0c;过滤列表中的偶数&#xff1a; List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

编程新知 2026/1/12 10:41:22

遍历 Map 类型集合的方法汇总

1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

编程新知 2026/1/24 15:08:45

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module

1、为什么要修改 CONNECT 报文&#xff1f; 多租户隔离&#xff1a;自动为接入设备追加租户前缀&#xff0c;后端按 ClientID 拆分队列。零代码鉴权&#xff1a;将入站用户名替换为 OAuth Access-Token&#xff0c;后端 Broker 统一校验。灰度发布&#xff1a;根据 IP/地理位写…...

编程新知 2025/8/1 10:20:23

质量体系的重要

质量体系是为确保产品、服务或过程质量满足规定要求&#xff0c;由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面&#xff1a; &#x1f3db;️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限&#xff0c;形成层级清晰的管理网络&#xf…...

编程新知 2025/10/24 9:13:44

相机从app启动流程

一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下： 重点代码分析： 启动相机前，先要通过getCameraIdList获取camera的个数以及id，然后可以通过getCameraCharacteristics获取对应id camera的capabilities（静态信息）进行一些openCamera前的…...

编程新知 2026/1/31 5:09:19

Module Federation 和 Native Federation 的比较

前言 Module Federation 是 Webpack 5 引入的微前端架构方案&#xff0c;允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

编程新知 2026/1/31 13:48:37

unix/linux，sudo，其发展历程详细时间线、由来、历史背景

sudo 的诞生和演化，本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来，让我们拨开时间的迷雾，一同探寻 sudo 那波澜壮阔（也颇为实用主义）的发展历程。 历史背景：su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前，Unix 系统管理员和需要特权操作的…...

编程新知 2025/11/18 21:31:41

SpringCloudGateway 自定义局部过滤器

场景&#xff1a; 将所有请求转化为同一路径请求&#xff08;方便穿网配置&#xff09;在请求头内标识原来路径&#xff0c;然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

编程新知 2026/2/1 4:53:36