数字孪生技术与VR:创造数字未来
在当今数字化浪潮中,数字孪生和虚拟现实(VR)技术是两大亮点,它们以独特的方式相互结合,为各个领域带来了创新和无限可能。本篇文章将探讨数字孪生与VR之间的关系,以及它们如何共同开辟未来的新前景。
数字孪生:现实世界的数字映射
数字孪生是一种虚拟技术,它通过数字模型的方式复制、映射和模拟现实世界中的事物、过程和系统。数字孪生模型包括从工厂和城市到供应链和医疗设施等各种领域。它们提供了复杂系统的深入理解,有助于提高效率、降低成本,以及更好地应对挑战。
虚拟现实:创造沉浸式体验
虚拟现实是一种技术,通过VR头戴设备将用户带入虚拟世界。在这个虚拟环境中,用户可以与数字内容互动,仿佛置身于虚拟世界之中。这种沉浸式体验使虚拟现实成为培训、娱乐、模拟和数据可视化等领域的有力工具。

数字孪生与VR:协同创新
数字孪生和虚拟现实的结合在各个领域中掀起了一股革命。首先,这一结合使得虚拟仿真环境成为可能。用户可以通过VR头戴设备沉浸式地体验数字孪生的虚拟版本。这意味着用户可以探索虚拟工厂、城市规划或医疗设施,同时感受到真实性。

此外,数字孪生和VR的结合支持了远程协作。在建筑和工程项目中,团队成员可以分布在不同地点,但通过VR技术,他们可以在数字孪生中实时合作,检查设计、解决问题和优化项目。

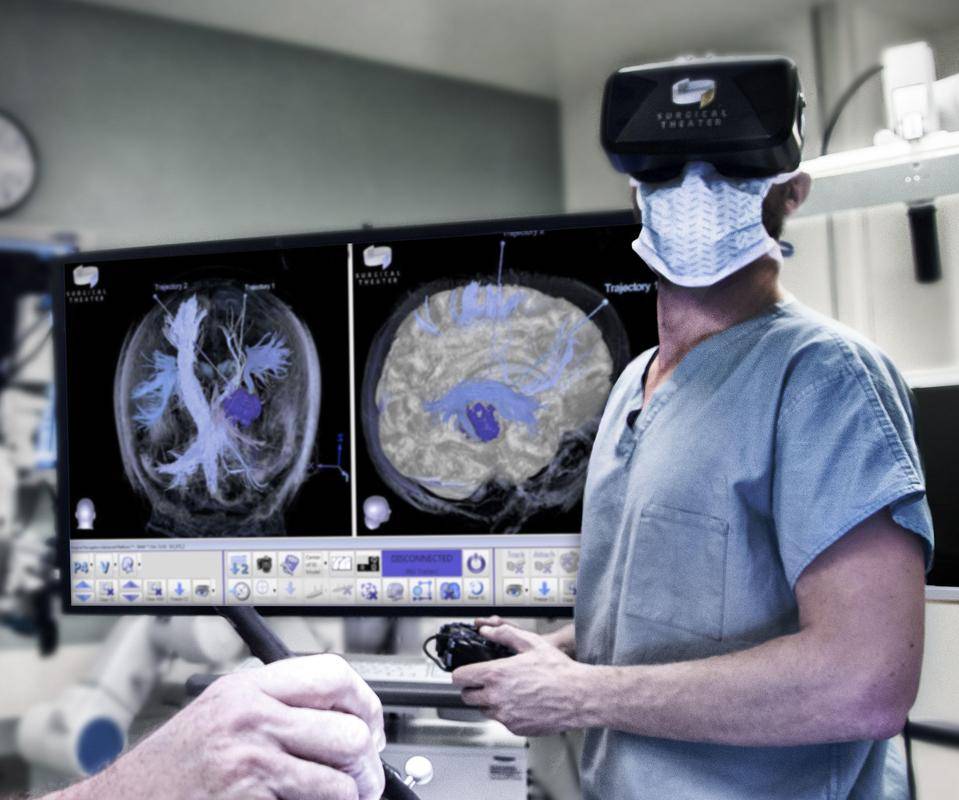
数字孪生与VR还在培训和模拟方面发挥了巨大作用。在医疗领域,医生可以通过虚拟现实进行手术培训,飞行员可以进行高度逼真的飞行模拟。这提供了一种安全且高效的学习方式。
此外,数据可视化也受益于数字孪生与VR的结合。数字孪生可以将复杂的数据和信息可视化,而VR提供了更直观、沉浸式的数据浏览体验。这有助于决策者更好地理解数据,制定更明智的决策。

最后,数字孪生和VR在娱乐和沉浸式体验领域有着巨大潜力。虚拟旅游允许用户探索全球各地的景点,而VR游戏将玩家带入想象中的世界。

数字孪生与虚拟现实的结合为各行各业带来了更多的机会和创新。它改变了我们与数字信息和虚拟环境互动的方式,为未来的科技发展提供了无限可能。在这个数字化时代,数字孪生与VR的结合将继续引领技术创新的浪潮,创造更多可能。
相关文章:

数字孪生技术与VR:创造数字未来
在当今数字化浪潮中,数字孪生和虚拟现实(VR)技术是两大亮点,它们以独特的方式相互结合,为各个领域带来了创新和无限可能。本篇文章将探讨数字孪生与VR之间的关系,以及它们如何共同开辟未来的新前景。 数字…...

系统架构设计师-第15章-面向服务架构设计理论与实践-软考学习笔记
面向服务的体系结构(Service-Oriented Architecture, SOA) 面向服务的体系结构(Service-Oriented Architecture, SOA)是一种软件架构模式,它将应用程序的不同功能组织为一组可重用的、松耦合的、自治的服务,这些服务通…...
为什么我觉得Rust比C++复杂得多?
为什么我觉得Rust比C复杂得多? Rust自学确实有一定门槛,很多具体问题解决起来搜索引擎也不太帮的上忙,会出现卡住的情况,卡的时间长了就放弃了。最近很多小伙伴找我,说想要一些c语言资料,然后我根据自己从…...
- 03 增删改查)
python sqlalchemy(ORM)- 03 增删改查
文章目录 ORM更新数据ORM查询ORM删除操作处理关系对象多表的关联查询 本节所有案例基于(第一节 python sqlalchemy(ORM)- 01 ORM简单使用)中的User、Address两个模型类 ORM更新数据 查询到模型类对象,直接修改其属性…...

Flutter笔记:完全基于Flutter绘图技术绘制一个精美的Dash图标(上)
Flutter笔记 完全基于Flutter绘图技术绘制一个精美的Dart语言吉祥物Dash(上) 作者:李俊才 (jcLee95):https://blog.csdn.net/qq_28550263 邮箱 :291148484163.com 本文地址:https://…...

学习gorm:彻底弄懂Find、Take、First和Last函数的区别
在gorm中,要想从数据库中查找数据有多种方法,可以通过Find、Take和First来查找。但它们之间又有一些不同。本文就详细介绍下他们之间的不同。 一、准备工作 首先我们有一个m_tests表,其中id字段是自增的主键,同时该表里有3条数据…...
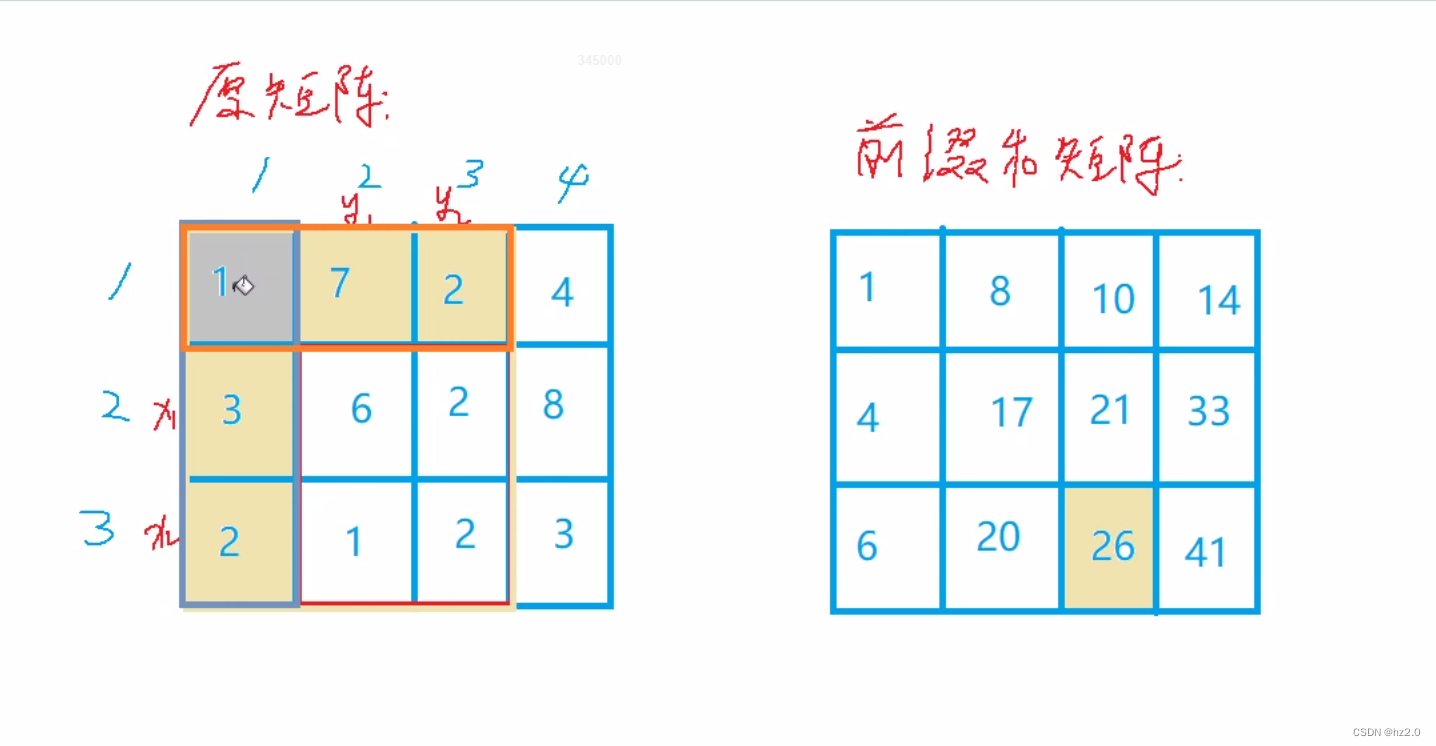
796. 子矩阵的和(二维前缀和)
题目: 796. 子矩阵的和 - AcWing题库 思路: 1.暴力搜索(搜索时间复杂度为O(n2),很多时候会超时) 2. 前缀和(左上角(二维)前缀和):本题特殊在不是直接求前…...
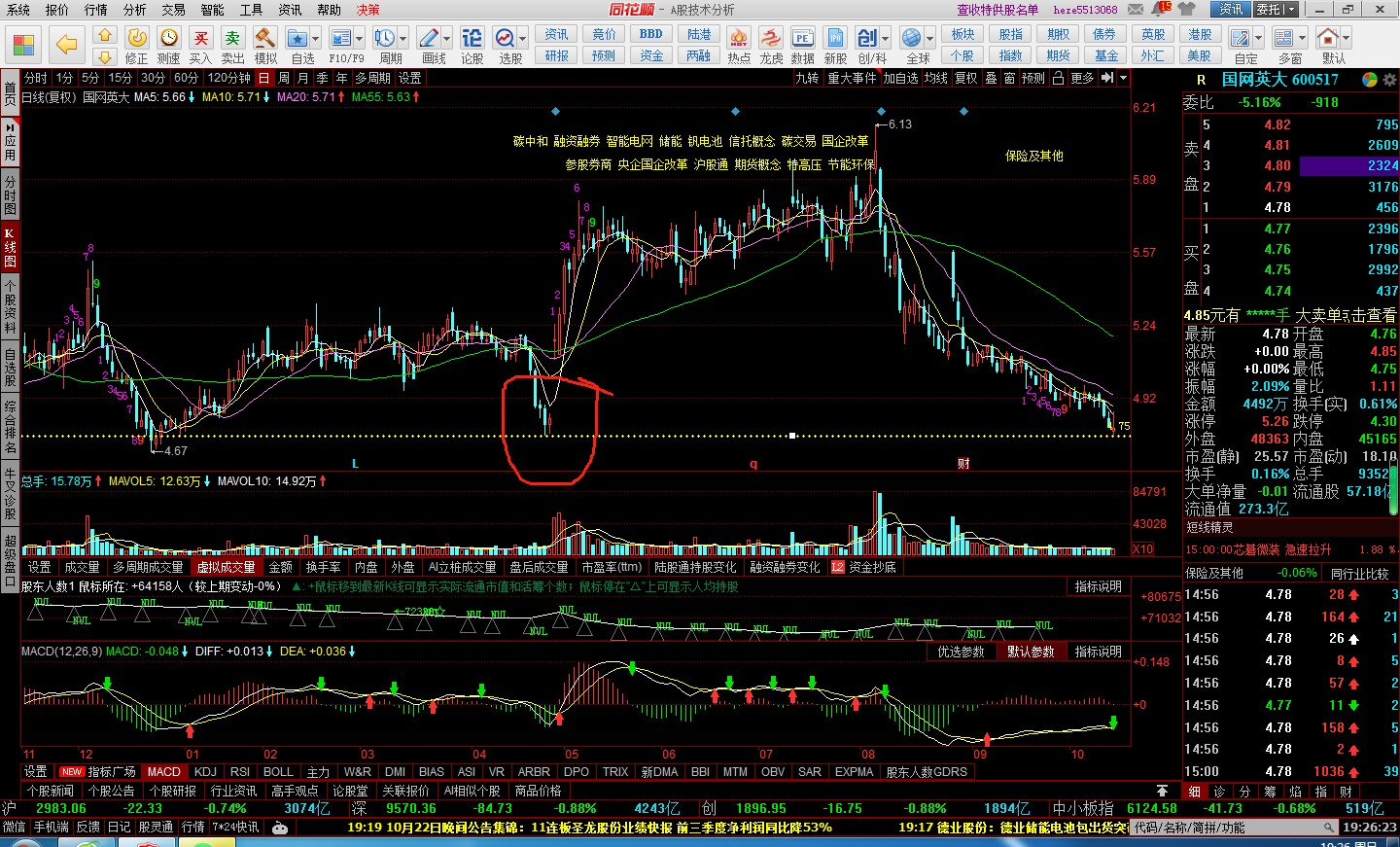
利用ChatGPT进行股票走势分析
文章目录 1. 股票分析2. 技巧分析3. 分析技巧21. 股票分析 这张图片显示了一个股票交易软件的界面。以下是根据图片内容的一些解读: 股票代码: 图片右上角显示的代码是“600517”,这是股票的代码。 图形解读: 该图展示了股票的日K线图。其中,蜡烛图表示每日的开盘、收盘、最…...
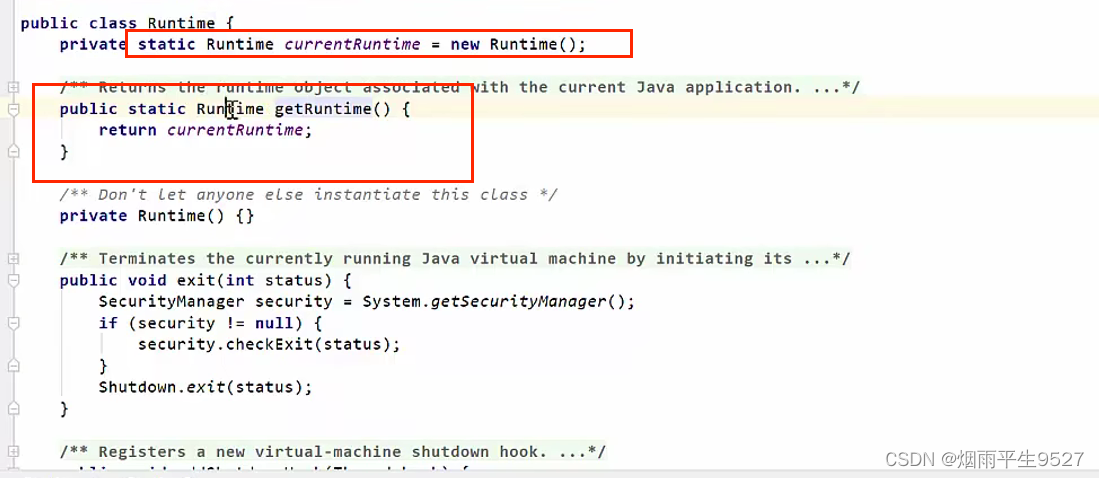
万字解析设计模式之单例模式
一、概述 1.1简介 单例模式(Singleton Pattern)是 Java 中最简单的设计模式之一。这种类型的设计模式属于创建型模式,它提供了一种创建对象的最佳方式。 这种模式涉及到一个单一的类,该类负责创建自己的对象,同时确保…...

vue2.x 二次封装element ui 中的el-dialog
在做后台管理系统的时候,dialog组件是我们使用频率比较高的组件,但是有一些需求现有的组件是不满足的。因此会需要我们做二次封装。 组件本身的属性我们保留,只需要根据需求添加,然后在使用的时候props去拿取使用就可以了。 本次遇…...

ssh连接Ubuntu虚拟机出现connection reset by ip地址 port 22怎么解决
使用前提:我是用Windows去连接安装在本机的Ubuntu虚拟机的时候出现的这个问题。 解决的方法:我使用了很多网络上方法,都没有用,发现我把IP地址搞错了 请继续看下去,因为有可能你会错过解决的方法。 在Windows网络连…...

树莓派4B安装ffmpeg
环境: piraspberrypi:~/x264 $ lsb_release -aNo LSB modules are available.Distributor ID: RaspbianDescription: Raspbian GNU/Linux 10 (buster)Release: 10Codename: buster 装H264 git clone --depth 1 https://code.videolan.org/video…...
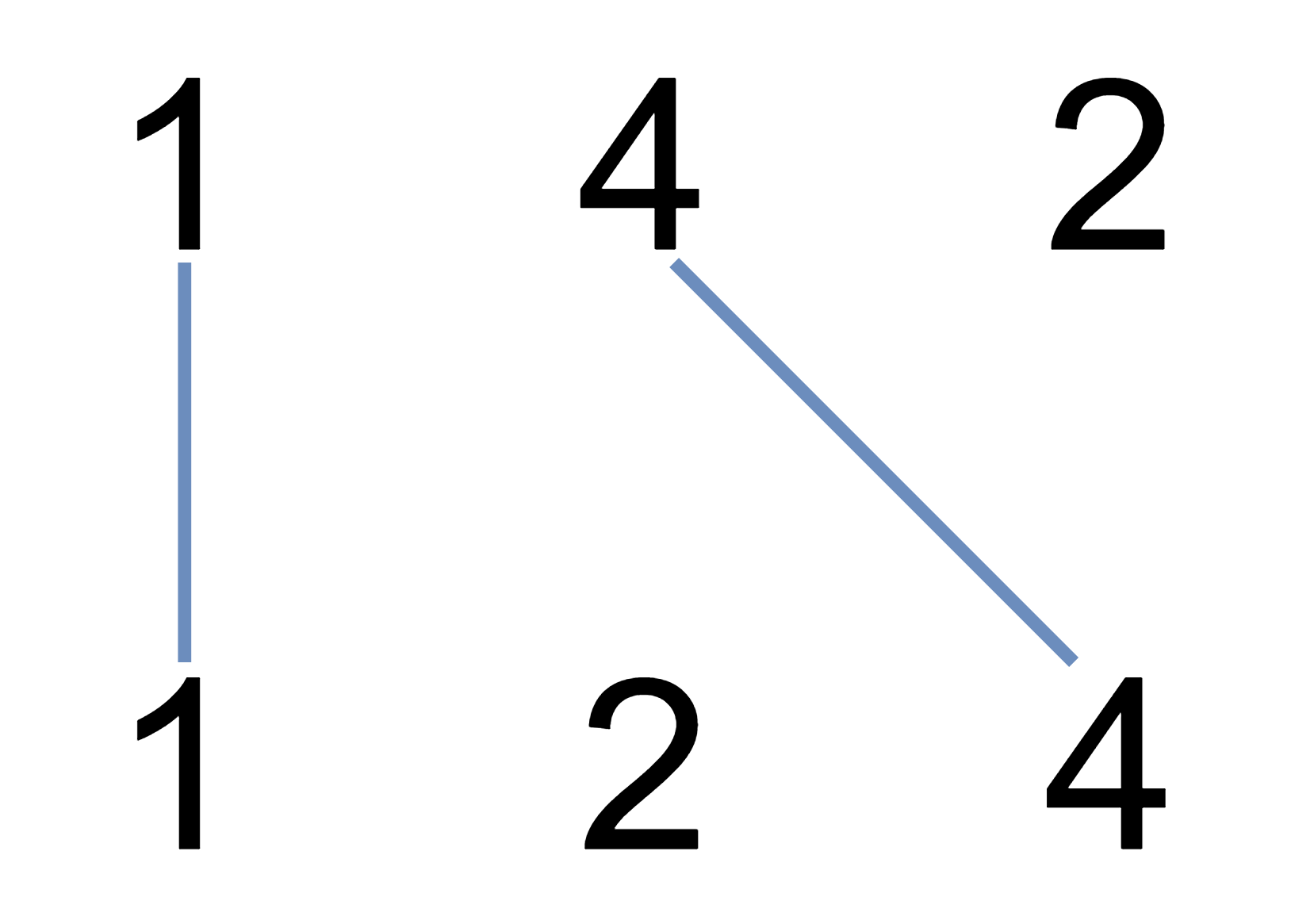
LeetCode|动态规划|1035. 不相交的线 、53. 最大子数组和
目录 一、1035. 不相交的线 1.题目描述 2.解题思路 3.代码实现 二、53. 最大子数组和 1.题目描述 2.解题思路 3.代码实现(动态规划解法) 一、1035. 不相交的线 1.题目描述 在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。 现…...
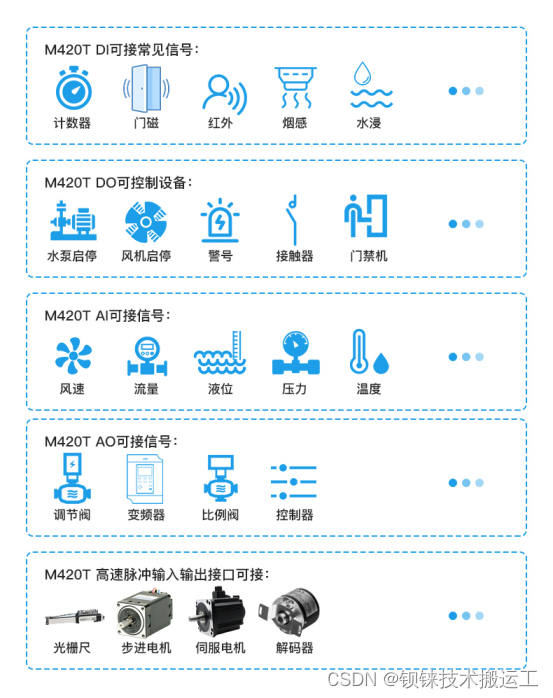
一体式IO模块:汽车行业的数字化转型助推器
随着市场经济需求的不断增长,汽车行业的自动化和智能化已经成为行业发展的必然趋势。在这个背景下,汽车行业的工作流程变得越来越复杂,工业机器人的广泛应用为汽车生产提供了强有力的支持,它们扮演着装配工、操作工、焊接工等多种…...

OpenCV官方教程中文版 —— Hough 直线变换
OpenCV官方教程中文版 —— Hough 直线变换 前言一、原理二、OpenCV 中的霍夫变换三、Probabilistic Hough Transform 前言 目标 • 理解霍夫变换的概念 • 学习如何在一张图片中检测直线 • 学习函数:cv2.HoughLines(),cv2.HoughLinesP() 一、原理…...
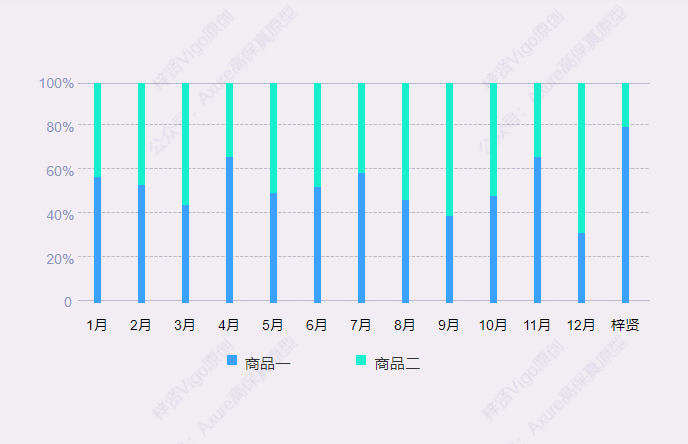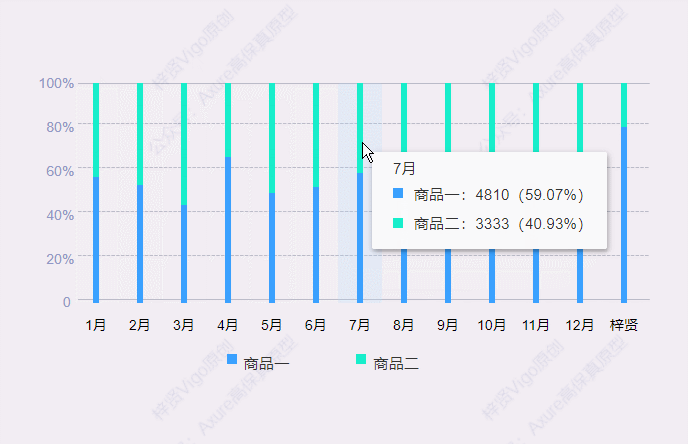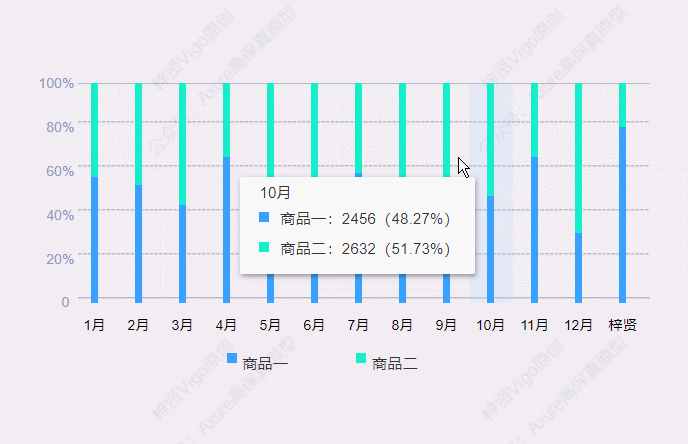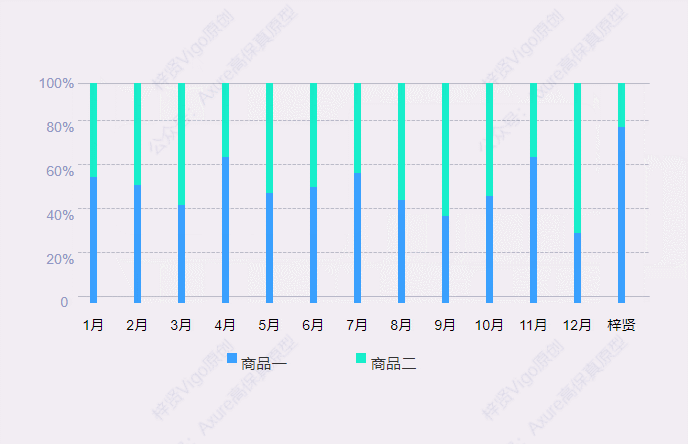
【Axure高保真原型】百分比堆叠柱状图
今天和大家分享百分比堆叠柱状图的的原型模板,鼠标移入堆叠柱状图后,会显示数据弹窗,里面可以查看具体项目对应的数据和占比。那这个原型模板是用中继器制作的,所以使用也很方便,只需要在中继器表格里维护项目数据信息…...

Vue.js中的双向数据绑定(two-way data binding)
聚沙成塔每天进步一点点 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 欢迎来到前端入门之旅!感兴趣的可以订阅本专栏哦!这个专栏是为那些对Web开发感兴趣、刚刚踏入前端领域的朋友们量身打造的。无论你是完全的新手还是有一些基础的开发…...

TFN 2.5G SDH传输分析仪 FT100-D300S
今天给大家带来一款TFN 2.5G SDH传输分析仪--TFN FT100-D300S. D300S SDH测试模块,是FT100智能网络测试平台产品家族的一部分,是一个坚固耐用、锂电池超长供电的传统PDH/SDH测试解决方案,支持2.5Gbps到2.048Mbps速率的传输链路测试。支持在线…...
电脑录像功能在哪?一文帮你轻松破解
“电脑录像功能在哪里呀?最近因工作上的原因,需要使用电脑来录像,但是找了一上午都找不到在哪里,眼看已经快没时间了,现在真的很急,希望大家帮帮我。” 电脑已经成为了人们生活和工作中必不可少的工具&…...

基于长短期神经网络的可上调容量PUP预测,基于长短期神经网络的可下调容量PDO预测,LSTM可调容量预测
目录 背影 摘要 代码和数据下载:基于长短期神经网络的可上调容量PUP预测,基于长短期神经网络的可下调容量PDO预测,LSTM可调容量预测(代码完整,数据齐全)资源-CSDN文库 https://download.csdn.net/download/abc991835105/88230834 LSTM的基本定义 LSTM实现的步骤 基于长短…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅!
【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅! 🌱 前言:一棵树的浪漫,从数组开始说起 程序员的世界里,数组是最常见的基本结构之一,几乎每种语言、每种算法都少不了它。可你有没有想过,一组看似“线性排列”的有序数组,竟然可以**“长”成一棵平衡的二…...

Vue3 PC端 UI组件库我更推荐Naive UI
一、Vue3生态现状与UI库选择的重要性 随着Vue3的稳定发布和Composition API的广泛采用,前端开发者面临着UI组件库的重新选择。一个好的UI库不仅能提升开发效率,还能确保项目的长期可维护性。本文将对比三大主流Vue3 UI库(Naive UI、Element …...
