C++深度优先(DFS)算法的应用:收集所有金币可获得的最大积分
涉及知识点
深度优化(DFS) 记忆化
题目
节点 0 处现有一棵由 n 个节点组成的无向树,节点编号从 0 到 n - 1 。给你一个长度为 n - 1 的二维 整数 数组 edges ,其中 edges[i] = [ai, bi] 表示在树上的节点 ai 和 bi 之间存在一条边。另给你一个下标从 0 开始、长度为 n 的数组 coins 和一个整数 k ,其中 coins[i] 表示节点 i 处的金币数量。
从根节点开始,你必须收集所有金币。要想收集节点上的金币,必须先收集该节点的祖先节点上的金币。
节点 i 上的金币可以用下述方法之一进行收集:
收集所有金币,得到共计 coins[i] - k 点积分。如果 coins[i] - k 是负数,你将会失去 abs(coins[i] - k) 点积分。
收集所有金币,得到共计 floor(coins[i] / 2) 点积分。如果采用这种方法,节点 i 子树中所有节点 j 的金币数 coins[j] 将会减少至 floor(coins[j] / 2) 。
返回收集 所有 树节点的金币之后可以获得的最大积分。
参数范围:
n == coins.length
2 <= n <= 105
0 <= coins[i] <= 104
edges.length == n - 1
0 <= edges[i][0], edges[i][1] < n
0 <= k <= 104
分析
时间复杂度
O(节点数量), DFS调用的次数=节点数量*2(两种方式)*21(分割方式),当n无穷大时,2和21忽略。
核心原理
当有祖先节点现在方式二时,本节点金币会减半。由于最多有10000个金币,所以减半15次后就是0,所以减半15次以上,和减半15次结果一样。比赛时,时间紧急,所以弄了20次,避免考虑边界情况。
变量解释
m_vRet[m_iN];//m_vRet[0] 未减半各节点及子孙节点的分数 m_vRet[i] 减半i次后的最大分数
代码
核心代码
class CNeiBo2
{
public:
CNeiBo2(int n, bool bDirect, int iBase = 0):m_iN(n),m_bDirect(bDirect),m_iBase(iBase)
{
m_vNeiB.resize(n);
}
CNeiBo2(int n, vector<vector>& edges, bool bDirect,int iBase=0) :m_iN(n), m_bDirect(bDirect), m_iBase(iBase)
{
m_vNeiB.resize(n);
for (const auto& v : edges)
{
m_vNeiB[v[0]- iBase].emplace_back(v[1]- iBase);
if (!bDirect)
{
m_vNeiB[v[1]- iBase].emplace_back(v[0]- iBase);
}
}
}
inline void Add(int iNode1, int iNode2)
{
iNode1 -= m_iBase;
iNode2 -= m_iBase;
m_vNeiB[iNode1].emplace_back(iNode2);
if (!m_bDirect)
{
m_vNeiB[iNode2].emplace_back(iNode1);
}
}
const int m_iN;
const bool m_bDirect;
const int m_iBase;
vector<vector> m_vNeiB;
};
class Solution {
public:
int maximumPoints(vector<vector>& edges, vector& coins, int k) {
m_iK = k;
for (int i = 0; i < m_iN; i++)
{
m_vRet[i].assign(coins.size(),-1);
}
CNeiBo2 neiBo(coins.size(),edges, false);
dfs(0, -1, 0, neiBo, coins);
return m_vRet[0][0];
}
int dfs(int cur, const int parent, int split,const CNeiBo2& vNeiBo,const vector& coins)
{
if (split >= 20)
{
return 0;
}
int& iRet = m_vRet[split][cur];
if (-1 != iRet)
{
return iRet;
}
const int curCoin = coins[cur] / (1 << split);
int iType1 = curCoin - m_iK;
{
for (const auto& next : vNeiBo.m_vNeiB[cur])
{
if (parent == next)
{
continue;
}
iType1 += dfs(next, cur, split, vNeiBo, coins);
}
}
int iType2 = curCoin/2;
{
for (const auto& next : vNeiBo.m_vNeiB[cur])
{
if (parent == next)
{
continue;
}
iType2 += dfs(next, cur, split+1, vNeiBo, coins);
}
}
iRet = max(iType1, iType2);
return iRet;
}
int m_iK;
static const int m_iN = 20;
vector m_vRet[m_iN];//m_vRet[0] 未减半各节点及子孙节点的分数 m_vRet[i] 减半i次后的最大分数
};
测试用例
template
void Assert(const vector& v1, const vector& v2)
{
if (v1.size() != v2.size())
{
assert(false);
return;
}
for (int i = 0; i < v1.size(); i++)
{
assert(v1[i] == v2[i]);
}
}
template
void Assert(const T& t1, const T& t2)
{
assert(t1 == t2);
}
int main()
{
Solution slu;
vector<vector> edges;
vector coins;
int k;
int res;
edges = { {0,1},{1,2},{2,3} };
coins = { 10,10,3,3 };
k = 5;
res = slu.maximumPoints(edges, coins,k);
Assert(11, res);
edges = { {0,1},{0,2} };
coins = { 8,4,4 };
k = 0;
res = slu.maximumPoints(edges, coins, k);
Assert(16, res);
//CConsole::Out(res);
}
扩展阅读
视频课程
有效学习:明确的目标 及时的反馈 拉伸区(难度合适),可以先学简单的课程,请移步CSDN学院,听白银讲师(也就是鄙人)的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快速形成战斗了,为老板分忧,请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176
相关下载
想高屋建瓴的学习算法,请下载《闻缺陷则喜算法册》doc版
https://download.csdn.net/download/he_zhidan/88348653
| 充满正能量得对大家说 |
|---|
| 闻缺陷则喜是一个美好的愿望,早发现问题,早修改问题,给老板节约钱。 |
| 墨家名称的来源:有所得以墨记之。 |
| 如果程序是一条龙,那算法就是他的是睛 |
测试环境
操作系统:win7 开发环境: VS2019 C++17
或者 操作系统:win10 开发环境: VS2022 C++17

相关文章:

C++深度优先(DFS)算法的应用:收集所有金币可获得的最大积分
涉及知识点 深度优化(DFS) 记忆化 题目 节点 0 处现有一棵由 n 个节点组成的无向树,节点编号从 0 到 n - 1 。给你一个长度为 n - 1 的二维 整数 数组 edges ,其中 edges[i] [ai, bi] 表示在树上的节点 ai 和 bi 之间存在一条边。另给你一个下标从 0…...

uniapp中APP端使用echarts用formatter设置y轴保留2位小数点不生效
uniapp使用echarts,在内置浏览器中,设置保留2位小数能正常显示(代码如下),但是在APP端这个设置不起作用。 yAxis: {type: value,axisLabel: {formatter: function (val) {return val.toFixed(2); //y轴始终保留小数点…...

无糖茶饮三十年,从无人问津到人手一瓶
【潮汐商业评论/原创】 Joan又在外卖上点了一堆瓶装茶饮,东方树叶、燃茶、三得利乌龙茶……买了四五种纯茶,用她的话说,和美式咖啡相比,这些无糖茶更适合他这个中国体质。 事实上,越来越多的消费者开始像Joan一样&am…...

面向Three.js开发者的3D自动纹理化开发包
DreamTexture.js 是面向 three.js 开发者的 3D 模型纹理自动生成与设置开发包,可以为 webGL 应用增加 3D 模型的快速自动纹理化能力。 图一为原始模型, 图二图三为贴图后的模型。提示词: city, Realistic , cinematic , Front view ,Game scene graph 1、…...

数字孪生技术与VR:创造数字未来
在当今数字化浪潮中,数字孪生和虚拟现实(VR)技术是两大亮点,它们以独特的方式相互结合,为各个领域带来了创新和无限可能。本篇文章将探讨数字孪生与VR之间的关系,以及它们如何共同开辟未来的新前景。 数字…...

系统架构设计师-第15章-面向服务架构设计理论与实践-软考学习笔记
面向服务的体系结构(Service-Oriented Architecture, SOA) 面向服务的体系结构(Service-Oriented Architecture, SOA)是一种软件架构模式,它将应用程序的不同功能组织为一组可重用的、松耦合的、自治的服务,这些服务通…...
为什么我觉得Rust比C++复杂得多?
为什么我觉得Rust比C复杂得多? Rust自学确实有一定门槛,很多具体问题解决起来搜索引擎也不太帮的上忙,会出现卡住的情况,卡的时间长了就放弃了。最近很多小伙伴找我,说想要一些c语言资料,然后我根据自己从…...
- 03 增删改查)
python sqlalchemy(ORM)- 03 增删改查
文章目录 ORM更新数据ORM查询ORM删除操作处理关系对象多表的关联查询 本节所有案例基于(第一节 python sqlalchemy(ORM)- 01 ORM简单使用)中的User、Address两个模型类 ORM更新数据 查询到模型类对象,直接修改其属性…...

Flutter笔记:完全基于Flutter绘图技术绘制一个精美的Dash图标(上)
Flutter笔记 完全基于Flutter绘图技术绘制一个精美的Dart语言吉祥物Dash(上) 作者:李俊才 (jcLee95):https://blog.csdn.net/qq_28550263 邮箱 :291148484163.com 本文地址:https://…...

学习gorm:彻底弄懂Find、Take、First和Last函数的区别
在gorm中,要想从数据库中查找数据有多种方法,可以通过Find、Take和First来查找。但它们之间又有一些不同。本文就详细介绍下他们之间的不同。 一、准备工作 首先我们有一个m_tests表,其中id字段是自增的主键,同时该表里有3条数据…...
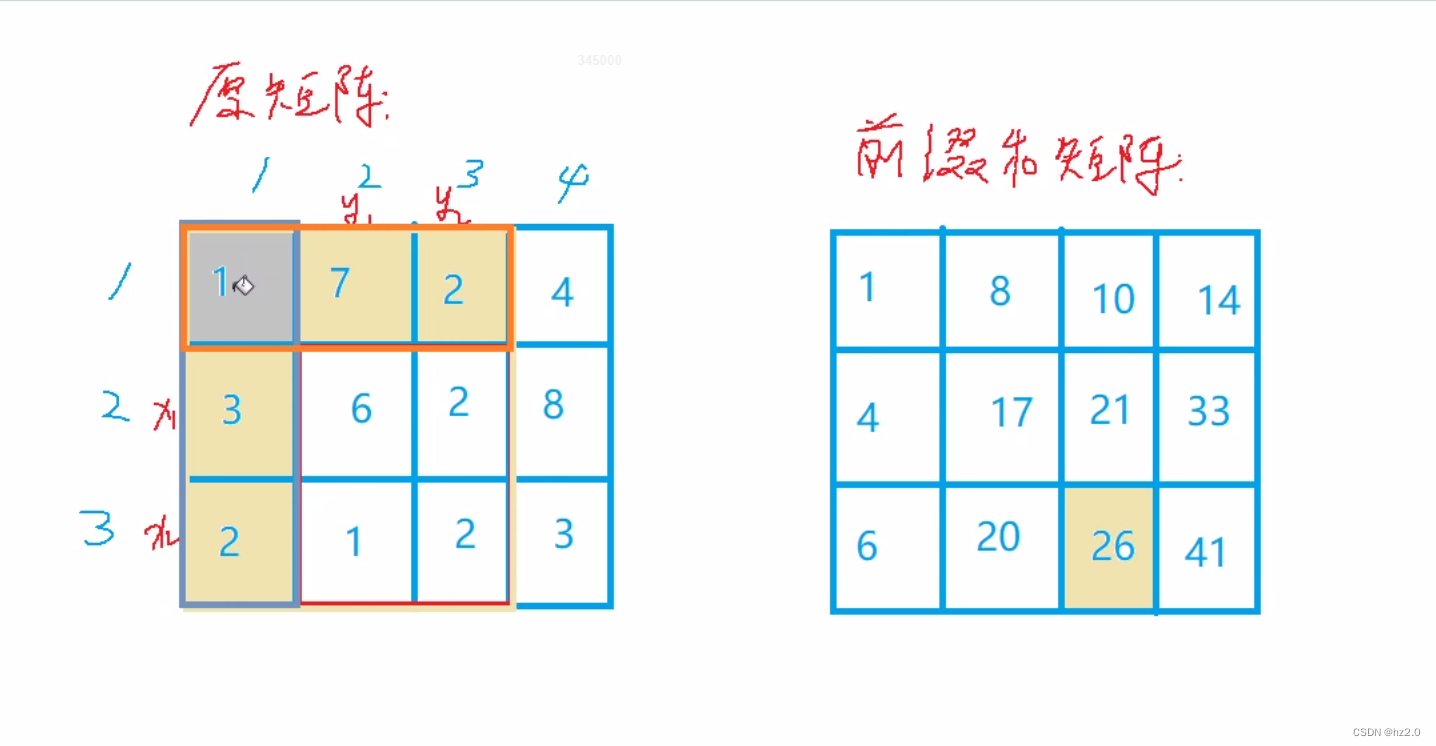
796. 子矩阵的和(二维前缀和)
题目: 796. 子矩阵的和 - AcWing题库 思路: 1.暴力搜索(搜索时间复杂度为O(n2),很多时候会超时) 2. 前缀和(左上角(二维)前缀和):本题特殊在不是直接求前…...
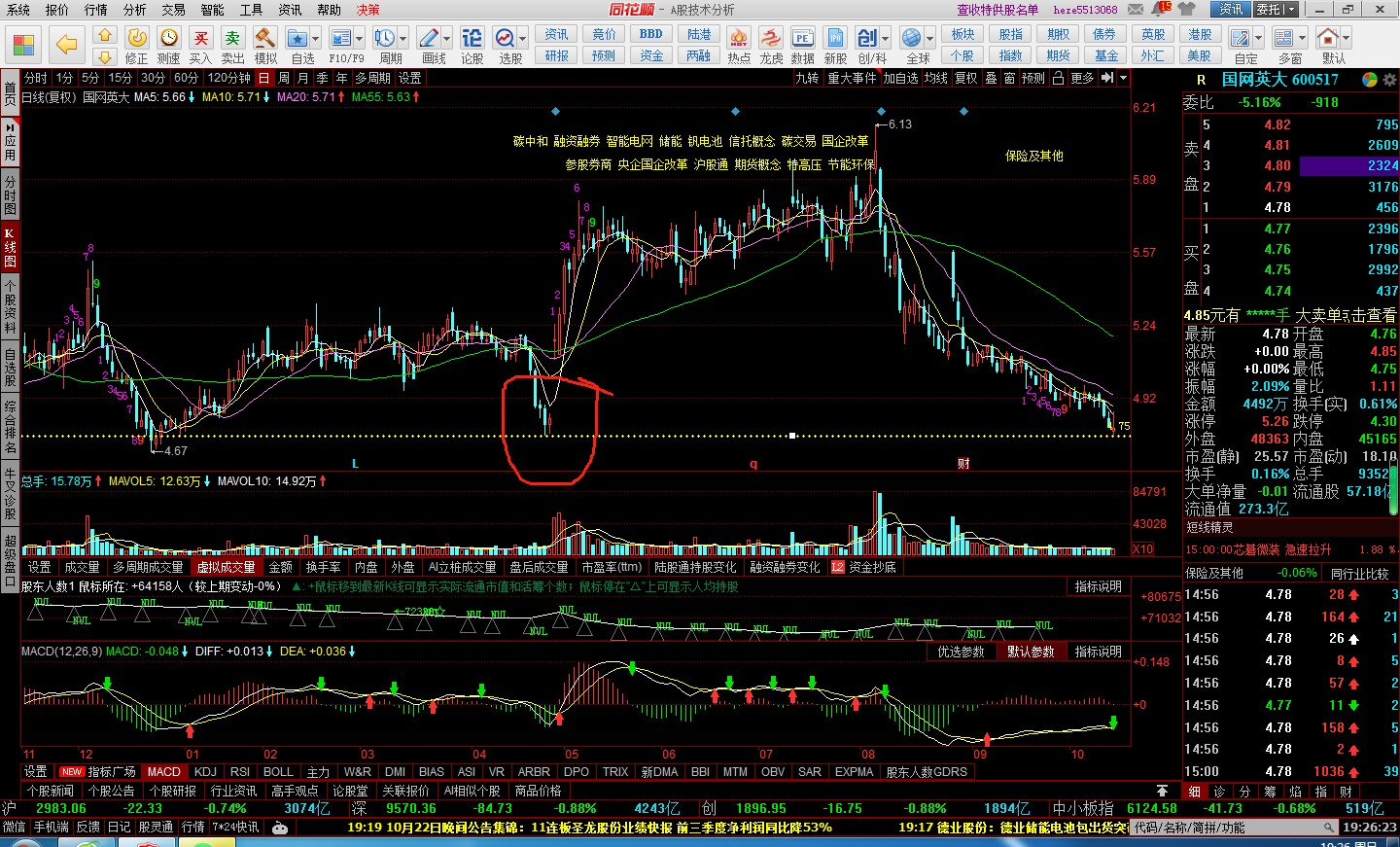
利用ChatGPT进行股票走势分析
文章目录 1. 股票分析2. 技巧分析3. 分析技巧21. 股票分析 这张图片显示了一个股票交易软件的界面。以下是根据图片内容的一些解读: 股票代码: 图片右上角显示的代码是“600517”,这是股票的代码。 图形解读: 该图展示了股票的日K线图。其中,蜡烛图表示每日的开盘、收盘、最…...
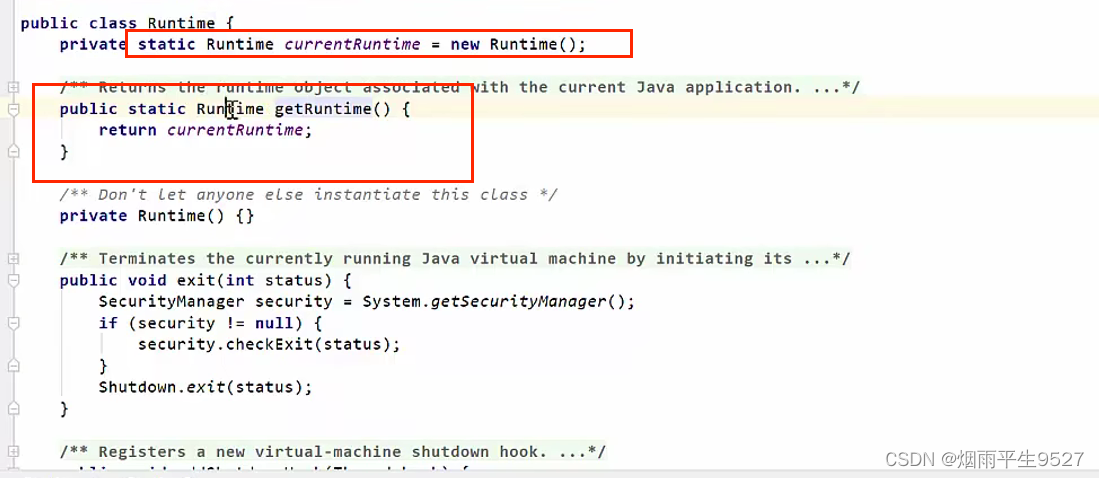
万字解析设计模式之单例模式
一、概述 1.1简介 单例模式(Singleton Pattern)是 Java 中最简单的设计模式之一。这种类型的设计模式属于创建型模式,它提供了一种创建对象的最佳方式。 这种模式涉及到一个单一的类,该类负责创建自己的对象,同时确保…...

vue2.x 二次封装element ui 中的el-dialog
在做后台管理系统的时候,dialog组件是我们使用频率比较高的组件,但是有一些需求现有的组件是不满足的。因此会需要我们做二次封装。 组件本身的属性我们保留,只需要根据需求添加,然后在使用的时候props去拿取使用就可以了。 本次遇…...

ssh连接Ubuntu虚拟机出现connection reset by ip地址 port 22怎么解决
使用前提:我是用Windows去连接安装在本机的Ubuntu虚拟机的时候出现的这个问题。 解决的方法:我使用了很多网络上方法,都没有用,发现我把IP地址搞错了 请继续看下去,因为有可能你会错过解决的方法。 在Windows网络连…...

树莓派4B安装ffmpeg
环境: piraspberrypi:~/x264 $ lsb_release -aNo LSB modules are available.Distributor ID: RaspbianDescription: Raspbian GNU/Linux 10 (buster)Release: 10Codename: buster 装H264 git clone --depth 1 https://code.videolan.org/video…...
LeetCode|动态规划|1035. 不相交的线 、53. 最大子数组和
目录 一、1035. 不相交的线 1.题目描述 2.解题思路 3.代码实现 二、53. 最大子数组和 1.题目描述 2.解题思路 3.代码实现(动态规划解法) 一、1035. 不相交的线 1.题目描述 在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。 现…...
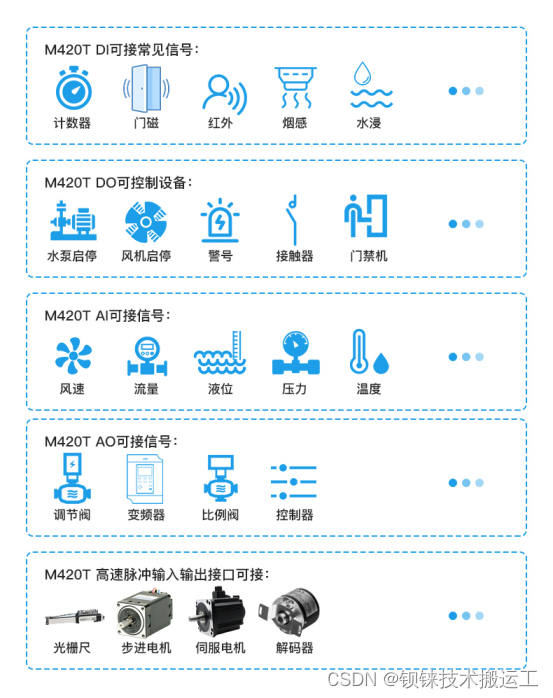
一体式IO模块:汽车行业的数字化转型助推器
随着市场经济需求的不断增长,汽车行业的自动化和智能化已经成为行业发展的必然趋势。在这个背景下,汽车行业的工作流程变得越来越复杂,工业机器人的广泛应用为汽车生产提供了强有力的支持,它们扮演着装配工、操作工、焊接工等多种…...

OpenCV官方教程中文版 —— Hough 直线变换
OpenCV官方教程中文版 —— Hough 直线变换 前言一、原理二、OpenCV 中的霍夫变换三、Probabilistic Hough Transform 前言 目标 • 理解霍夫变换的概念 • 学习如何在一张图片中检测直线 • 学习函数:cv2.HoughLines(),cv2.HoughLinesP() 一、原理…...
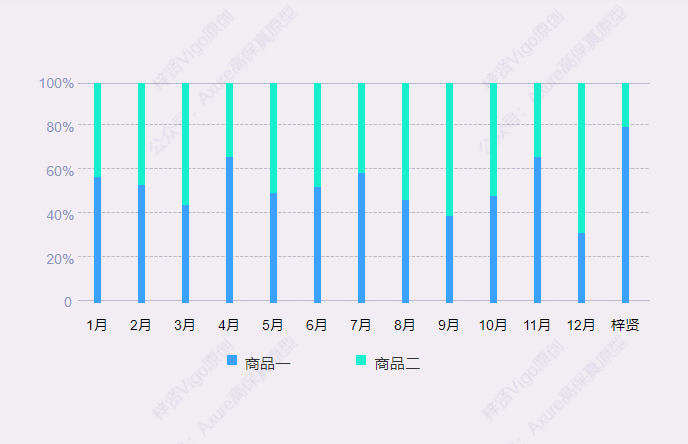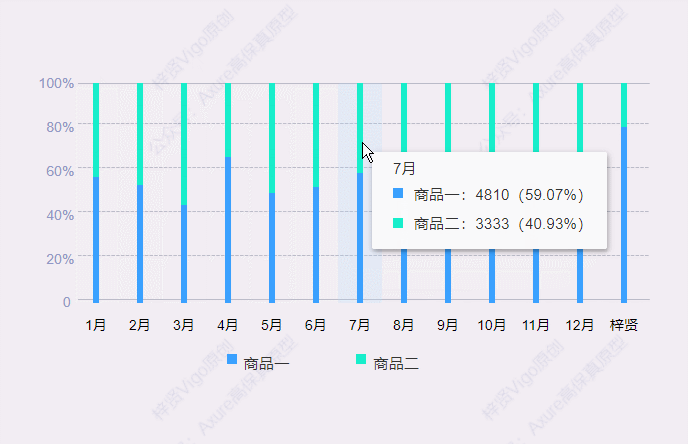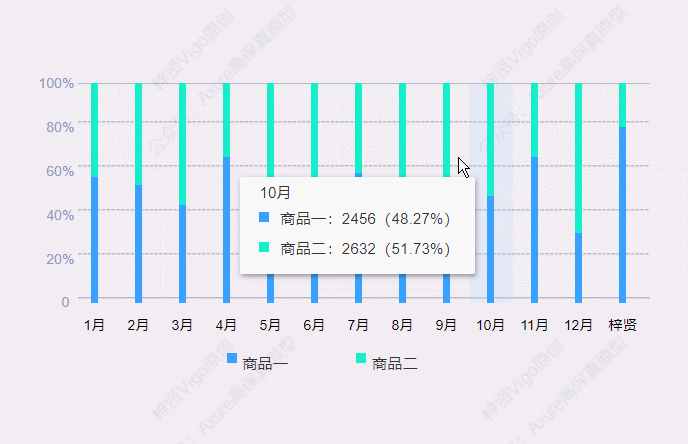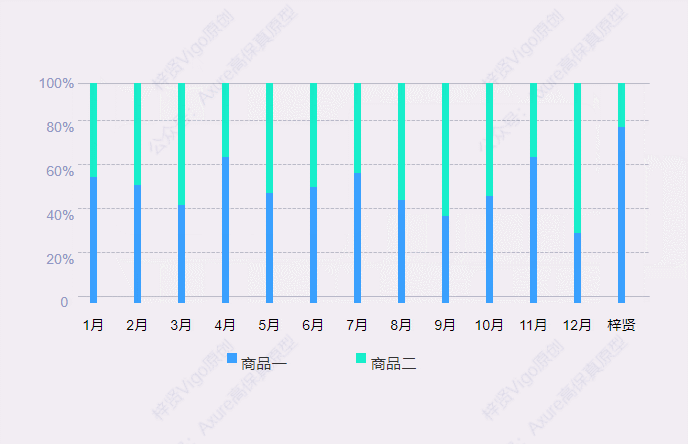
【Axure高保真原型】百分比堆叠柱状图
今天和大家分享百分比堆叠柱状图的的原型模板,鼠标移入堆叠柱状图后,会显示数据弹窗,里面可以查看具体项目对应的数据和占比。那这个原型模板是用中继器制作的,所以使用也很方便,只需要在中继器表格里维护项目数据信息…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...

Python训练营-Day26-函数专题1:函数定义与参数
题目1:计算圆的面积 任务: 编写一个名为 calculate_circle_area 的函数,该函数接收圆的半径 radius 作为参数,并返回圆的面积。圆的面积 π * radius (可以使用 math.pi 作为 π 的值)要求:函数接收一个位置参数 radi…...

QT开发技术【ffmpeg + QAudioOutput】音乐播放器
一、 介绍 使用ffmpeg 4.2.2 在数字化浪潮席卷全球的当下,音视频内容犹如璀璨繁星,点亮了人们的生活与工作。从短视频平台上令人捧腹的搞笑视频,到在线课堂中知识渊博的专家授课,再到影视平台上扣人心弦的高清大片,音…...

PH热榜 | 2025-06-08
1. Thiings 标语:一套超过1900个免费AI生成的3D图标集合 介绍:Thiings是一个不断扩展的免费AI生成3D图标库,目前已有超过1900个图标。你可以按照主题浏览,生成自己的图标,或者下载整个图标集。所有图标都可以在个人或…...
