AVL树、红黑树的介绍和实现[C++]
本文主要对AVL树和红黑树的结构和实现方法进行一定的介绍,仅实现部分接口。
目录
一、AVL树
1.AVL树的概念
2.AVL树节点的定义
3.AVL树的插入
4.AVL树的旋转
1. 新节点插入较高左子树的左侧——左左:右单旋
2. 新节点插入较高右子树的右侧——右右:左单旋
3. 新节点插入较高左子树的右侧——左右:先左单旋再右单旋
4. 新节点插入较高右子树的左侧——右左:先右单旋再左单旋
5.AVL树的验证
6.AVL树的性能
二、红黑树
1.红黑树的概念
2.红黑树的性质
3.红黑树节点的定义
4.红黑树的插入操作
1.情况一:cur为红,p为红,g为黑,u存在且为红
2.情况二: cur为红,p为红,g为黑,u不存在/u存在且为黑
3.情况三: cur为红,p为红,g为黑,u不存在/u存在且为黑
4.代码如下:
5.红黑树的验证
6.红黑树与AVL树的比较
前言
map/multimap/set/multiset介绍和使用
二叉搜索树介绍和实现
上一篇文章对map/multimap/set/multiset进行了简单的介绍,在其文档介绍中发现,这几个容器有个共同点是:其底层都是按照二叉搜索树来实现的,但是二叉搜索树有其自身的缺陷,假如往树中 插入的元素有序或者接近有序,二叉搜索树就会退化成单支树,时间复杂度会退化成O(N),因此 map、set等关联式容器的底层结构是对二叉树进行了平衡处理,即采用平衡树来实现。
一、AVL树
1.AVL树的概念
二叉搜索树虽可以缩短查找的效率,但如果数据有序或接近有序二叉搜索树将退化为单支树,查 找元素相当于在顺序表中搜索元素,效率低下。
因此,两位俄罗斯的数学家G.M.Adelson-Velskii 和E.M.Landis在1962年发明了一种解决上述问题的方法:当向二叉搜索树中插入新结点后,如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整),即可降低树的高度,从而减少平均搜索长度。
一棵AVL树或者是空树,或者是具有以下性质的二叉搜索树:
- 它的左右子树都是AVL树
- 左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)
(平衡因子只是一种AVL的实现方式,本文通过这种方法来实现)
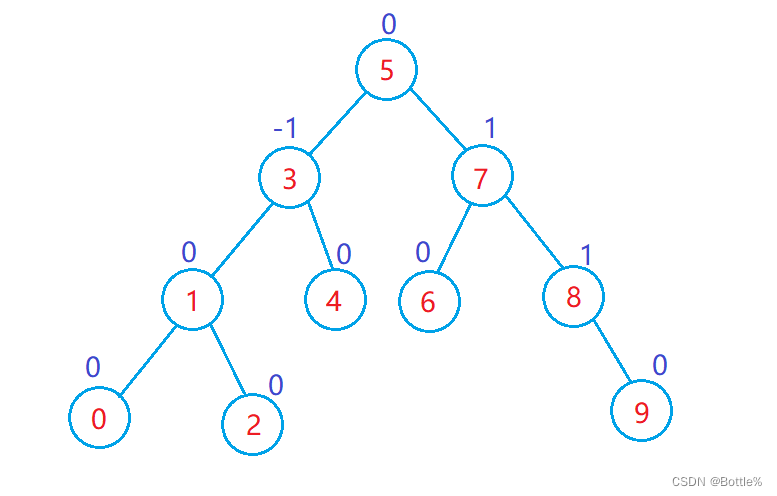
如果一棵二叉搜索树是高度平衡的,它就是AVL树。如果它有n个结点,其高度可保持在 ,搜索时间复杂度
。
2.AVL树节点的定义
AVL树节点的定义:
template<class K,class V>
struct AVLTreeNode
{AVLTreeNode(const pair<K, V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _bf(0){}AVLTreeNode<T>* _left; // 该节点的左孩子AVLTreeNode<T>* _right; // 该节点的右孩子AVLTreeNode<T>* _parent; // 该节点的双亲pair<K, V> _kv;int _bf; // 该节点的平衡因子
};3.AVL树的插入
AVL树就是在二叉搜索树的基础上引入了平衡因子,因此AVL树也可以看成是二叉搜索树。那么 AVL树的插入过程可以分为以下步骤:
- 按照二叉搜索树的方式找到其对应的位置插入新节点
- 调整节点的平衡因子,平衡因子的更新取决于子树高度的变化,左子树新增则--平衡因子,右子树新增++平衡因子
- 如果更新完以后,平衡没有出现问题,即 |_bf|<=1,平衡结构没有受到影响,不需要处理
- 如果更新完以后,平衡没有出现问题,即 |_bf|>1,平衡结构受到影响,需要旋转处理
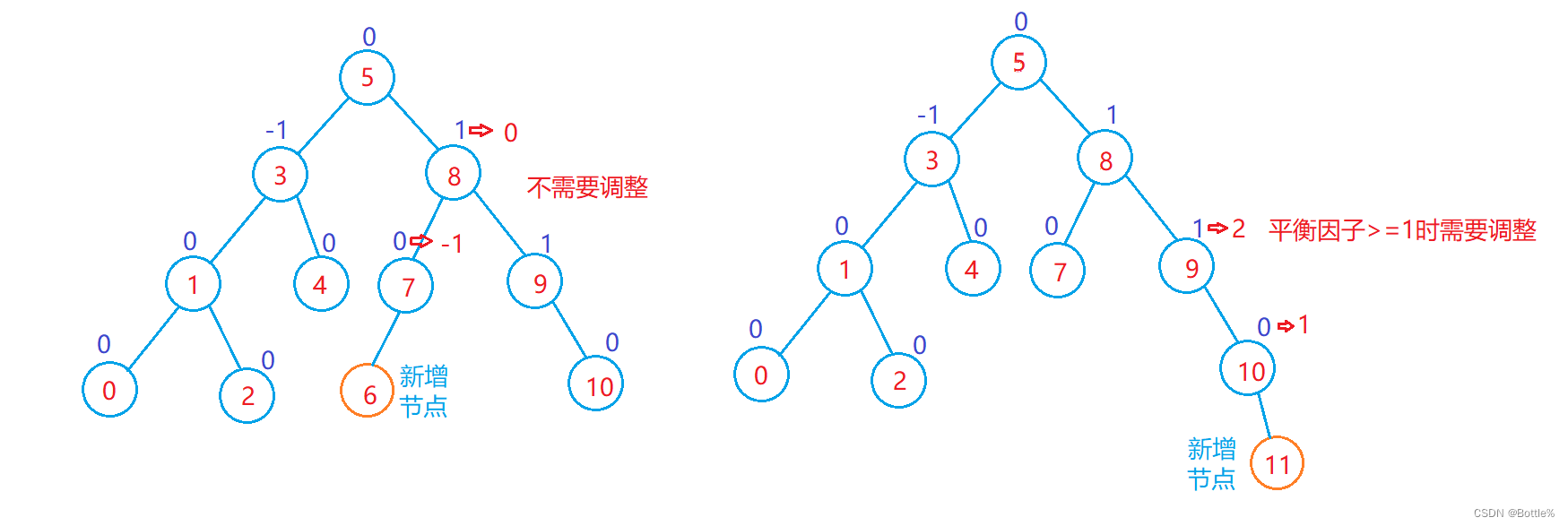
其中,新节点插入后,父节点的平衡因子一定需要调整,在插入之前,父节点的平衡因子分为三种情况: - 1,0, 1, 分以下两种情况:
- 如果新节点插入到父节点的左侧,只需给父节点的平衡因子 - 1即可
- 如果新节点插入到父节点的右侧,只需给父节点的平衡因子 + 1即可
此时:父节点的平衡因子可能有三种情况:0,正负1,正负2。
- 如果父节点的平衡因子为0,说明插入之前parent的平衡因子为正负1,插入后被调整成0,此时满足AVL树的性质,插入成功
- 如果父节点的平衡因子为正负1,说明插入前父节点的平衡因子一定为0,插入后被更新成正负1,此时以父节点为根的树的高度增加,需要继续向上更新
- 如果parent的平衡因子为正负2,则parent的平衡因子违反平衡树的性质,需要对其进行旋转处理
bool Insert(const pair<K, V>& kv)
{//寻找插入位置if (_root == nullptr){_root = new Node(kv);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else{return false;}}cur = new Node(kv);cur->_parent = parent;if (parent->_kv.first > kv.first){parent->_left = cur;}else{parent->_right = cur;}//调整平衡因子while (parent){if (parent->_left == cur)parent->_bf--;elseparent->_bf++;if (parent->_bf == 1 || parent->_bf == -1){parent = parent->_parent;cur = cur->_parent;}else if(parent->_bf == 0){break;}//进行旋转调整else if (parent->_bf == 2 || parent->_bf == -2){if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);}else if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}else if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);}else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);}break;}else{assert(false);}}
}4.AVL树的旋转
如果在一棵原本是平衡的AVL树中插入一个新节点,可能造成不平衡,此时必须调整树的结构, 使之平衡化。根据节点插入位置的不同,AVL树的旋转分为四种:
1. 新节点插入较高左子树的左侧——左左:右单旋
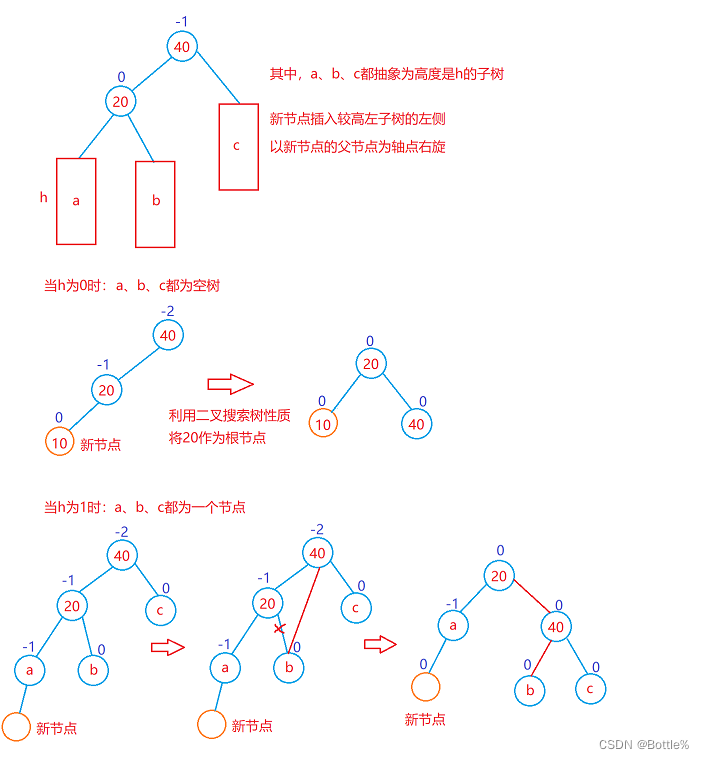

上图在插入前,AVL树是平衡的,新节点插入到20的左子树(注意:此处不是左孩子)中,20左子树增加了一层,导致以40为根的二叉树不平衡,要让40平衡,只能将40左子树的高度减少一层,右子树增加一层, 即将左子树往上提,这样40转下来,因为40比20大,只能将其放在20的右子树,而如果20有右子树,右子树根的值一定大于20,小于40,只能将其放在40的左子树,旋转完成后,更新节点的平衡因子即可。
代码如下:
void RotateR(Node* parent)//parent为平衡因子为-2的节点
{Node* subL = parent->_left;//parent的左孩子Node* subLR = subL->_right;//parent左孩子的右孩子,即需要更新为parent的新左孩子的节点parent->_left = subLR;// 如果20的左孩子的右孩子存在,更新父节点if (subLR)subLR->_parent = parent;subL->_right = parent;Node* ppnode = parent->_parent;parent->_parent = subL;// 如果40是根节点,根新指向根节点的指针if (ppnode == nullptr){_root = subL;_root->_parent = nullptr;}else{// 如果40是子树,可能是其双亲的左子树,也可能是右子树subL->_parent = ppnode;if (ppnode->_left == parent){ppnode->_left = subL;}else{ppnode->_right = subL;}}//根据调整后的结构更新部分节点的平衡因子parent->_bf = subL->_bf = 0;
}2. 新节点插入较高右子树的右侧——右右:左单旋

该情况为右右单旋的镜像,实现及情况考虑参考右单旋即可。
代码如下:
void RotateL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if(subRL)subRL->_parent = parent;subR->_left = parent;Node* ppnode = parent->_parent;parent->_parent = subR;if (ppnode == nullptr){_root = subR;_root->_parent = nullptr;}else{subR->_parent = ppnode;if (ppnode->_left == parent){ppnode->_left = subR;}else{ppnode->_right = subR;}}parent->_bf = subR->_bf = 0;
}3. 新节点插入较高左子树的右侧——左右:先左单旋再右单旋
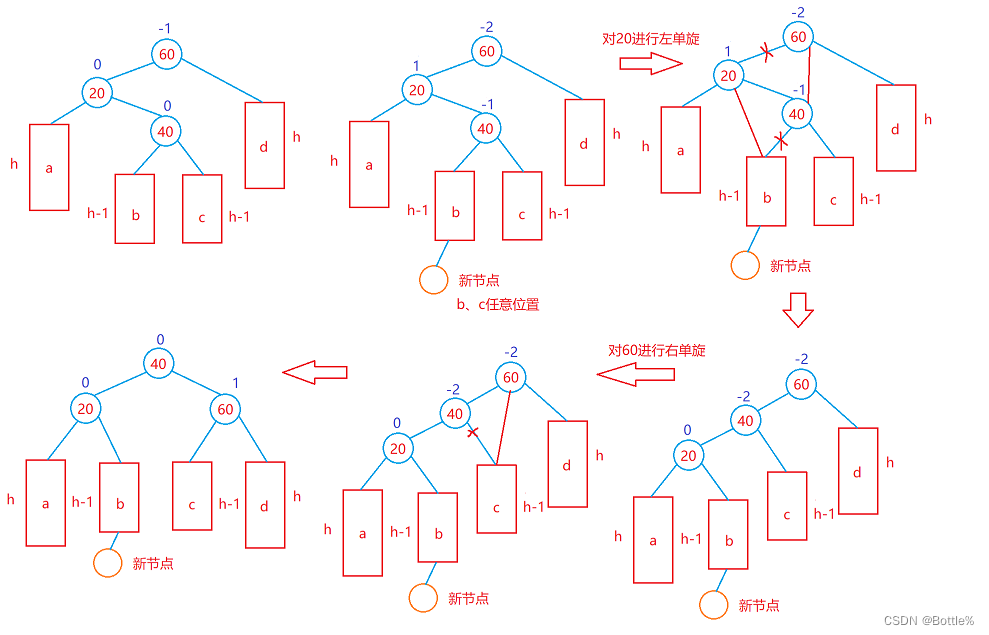
将双旋变成单旋后再旋转,即:先对20进行左单旋,然后再对60进行右单旋,旋转完成后再考虑平衡因子的更新。
代码如下:
// 旋转之前,40的平衡因子可能是-1/0/1,旋转完成之后,
//根据情况对其他节点的平衡因子进行调整
void RotateLR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;// 旋转之前,保存pSubLR的平衡因子,旋转完成之后,
// 需要根据该平衡因子来调整其他节点的平衡因子int bf = subLR->_bf;
// 先对20进行左单旋RotateL(parent->_left);// 再对60进行右单旋RotateR(parent);if (bf == -1){parent->_bf = 1;subLR->_bf = 0;subL->_bf = 0;}else if (bf == 1){parent->_bf = 0;subLR->_bf = 0;subL->_bf = -1;}else if (bf == 0){parent->_bf = 0;subLR->_bf = 0;subL->_bf = 0;}else//如果运行到此处说明平衡因子有错误assert(false);
}4. 新节点插入较高右子树的左侧——右左:先右单旋再左单旋
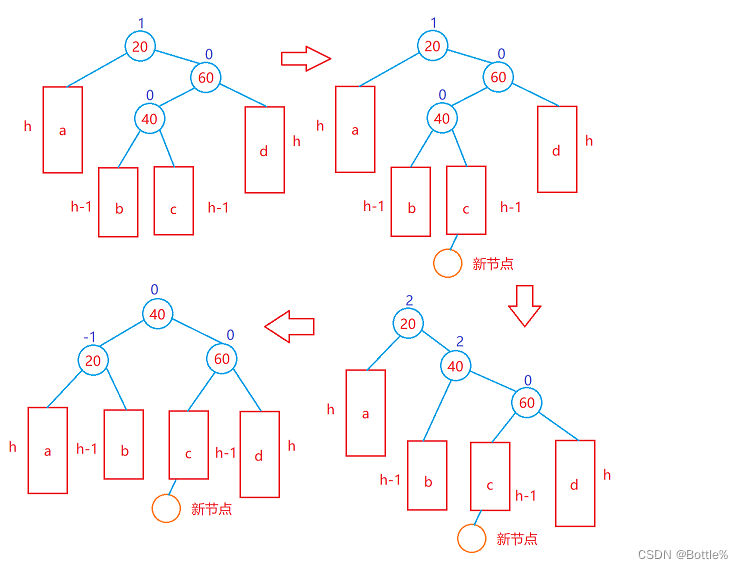
参考左右双旋。
代码如下:
void RotateRL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(parent->_right);RotateL(parent);if (bf == -1){parent->_bf = 0;subRL->_bf = 0 ;subR->_bf = 1;}else if (bf == 1){parent->_bf = -1;subRL->_bf = 0;subR->_bf = 0;}else if (bf == 0){parent->_bf = 0;subRL->_bf = 0;subR->_bf = 0;}elseassert(false);
}总结:
假如以parent为根的子树不平衡,即parent的平衡因子为2或者-2,分以下情况考虑
1. parent的平衡因子为2,说明parent的右子树高,设parent的右子树的根为subR
- 当subR的平衡因子为1时,执行左单旋
- 当subR的平衡因子为-1时,执行右左双旋
2. parent的平衡因子为-2,说明parent的左子树高,设parent的左子树的根为subL
- 当subL的平衡因子为-1是,执行右单旋
- 当subL的平衡因子为1时,执行左右双旋
5.AVL树的验证
AVL树是在二叉搜索树的基础上加入了平衡性的限制,因此要验证AVL树,可以分两步:
1. 验证其为二叉搜索树
如果中序遍历可得到一个有序的序列,就说明为二叉搜索树
2. 验证其为平衡树
- 每个节点子树高度差的绝对值不超过1(注意节点中如果没有平衡因子)
- 节点的平衡因子是否计算正确
int _Height(Node* root)//求树的高度
{if (root == nullptr)//为空返回0return 0;//递归求左子树和右子树的高度int left = _Height(root->_left);int right = _Height(root->_right);//返回较高子树的高度+1(根节点)return left > right ? left + 1 : right + 1;
}bool _IsBalance(Node* root)判断是否平衡
{if (root == nullptr)return true;int leftH = _Height(root->_left);int rightH = _Height(root->_right);//右子树高度-左子树高度!=平衡因子则说明有误if ((rightH - leftH) != root->_bf){ cout <<root->_kv.first<< "平衡因子错误" << endl;return false;}//平衡因子小于2,去递归左右子树return (abs(leftH - rightH) < 2)&& _IsBalance(root->_left)&& _IsBalance(root->_right);}bool IsBalance()
{return _IsBalance(_root);
}因为AVL树也是二叉搜索树,其他接口与二叉搜索树类似,其中删除接口可按照二叉搜索树的方式将节点删除,然后再更新平衡因子,只不过与删除不同的是,删除节点后的平衡因子更新,最差情况下一直要调整到根节点的位置。
本文主要介绍结构,其他接口实现不做介绍了。
6.AVL树的性能
AVL树是一棵绝对平衡的二叉搜索树,其要求每个节点的左右子树高度差的绝对值都不超过1,这 样可以保证查询时高效的时间复杂度,即。但是如果要对AVL树做一些结构修改的操作,性能非常低下,比如:插入时要维护其绝对平衡,旋转的次数比较多,更差的是在删除时, 有可能一直要让旋转持续到根的位置。因此:如果需要一种查询高效且有序的数据结构,而且数据的个数为静态的(即不会改变),可以考虑AVL树,但一个结构经常修改,就不太适合。
二、红黑树
1.红黑树的概念
红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或 Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出两倍,因而是接近平衡的。
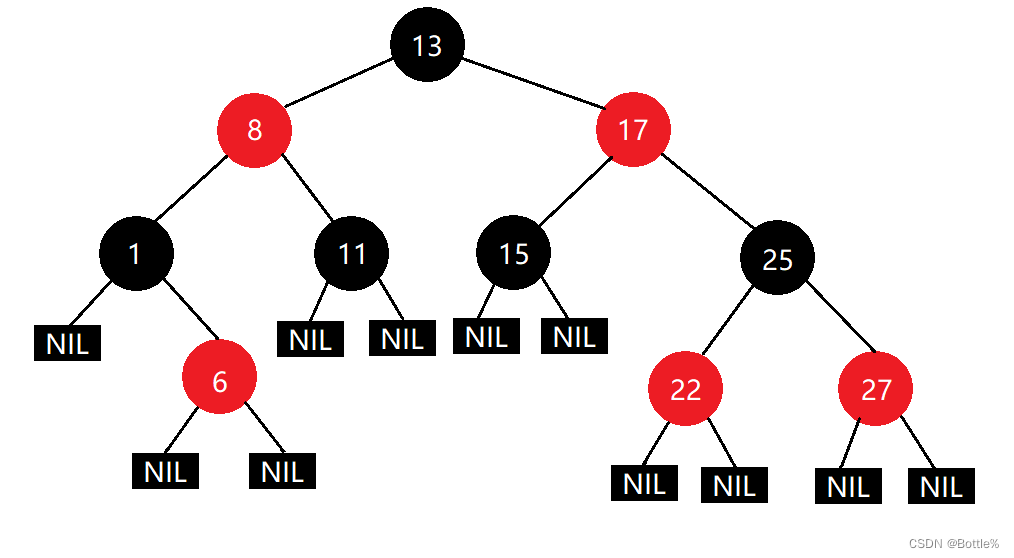
2.红黑树的性质
1. 每个结点不是红色就是黑色
2. 根节点是黑色的
3. 如果一个节点是红色的,则它的两个孩子结点是黑色的
4. 对于每个结点,从该结点到其所有后代叶结点的简单路径上,均包含相同数目的黑色结点
5. 每个叶子结点都是黑色的(此处的叶子结点指的是空结点)
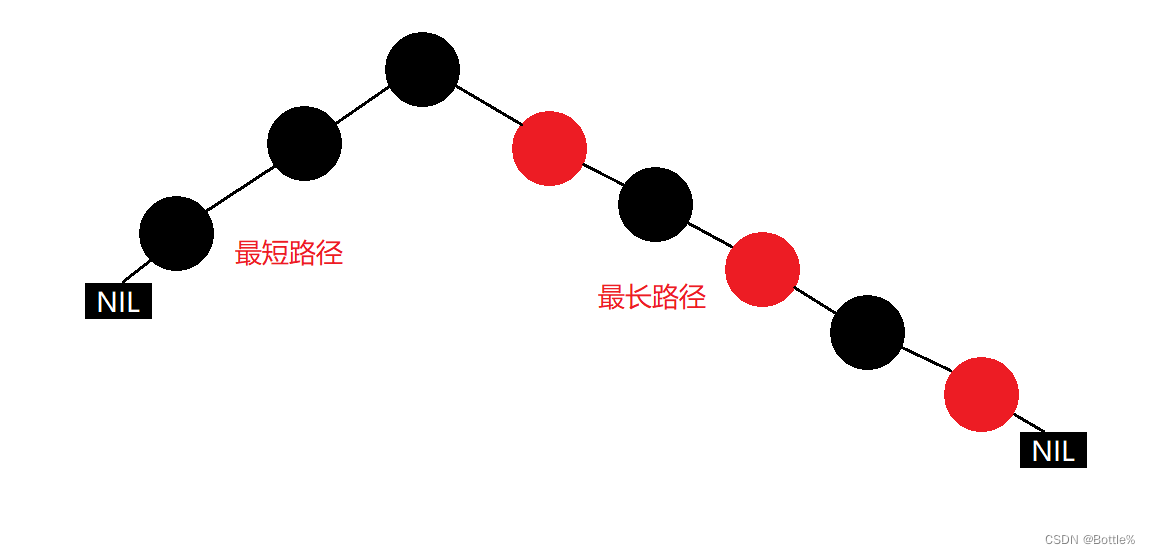
其中,根据性质3,4可以得到一条路径最短的情况为该路径都是黑节点,最长路径的情况为该路径上的节点为一黑一红交替,因此红黑树的最长路径最多为最短路径的2倍。
3.红黑树节点的定义
enum Color// 节点的颜色
{RED,BLACK
};
// 红黑树节点的定义
template<class K, class V>
struct RBTreeNode
{RBTreeNode<K, V>* _left;// 节点的左孩子RBTreeNode<K, V>* _right;// 节点的右孩子RBTreeNode<K, V>* _parent; // 节点的双亲(红黑树需要旋转)pair<K, V> _kv; // 节点的值域Color _col; // 节点的颜色RBTreeNode(const pair<K, V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _col(RED){}
};将新插入节点的默认颜色设置为红色。
如果新插入节点默认颜色为黑色的话,该节点插入后会违反性质4,那么需要对全部路径进行调整。新插入节点默认颜色为红色的话,如果该节点插入后父节点为黑色,则不需要调整,父节点为红色再继续调整。
根据上述情况,新插入节点默认颜色为红色更优。
4.红黑树的插入操作
红黑树是在二叉搜索树的基础上加上其平衡限制条件,因此红黑树的插入可分为两步:
1. 按照二叉搜索的树规则插入新节点
2. 检测新节点插入后,红黑树的性质是否造到破坏
因为新节点的默认颜色是红色,因此:如果其双亲节点的颜色是黑色,没有违反红黑树任何性质,则不需要调整;但当新插入节点的双亲节点颜色为红色时,就违反了性质3不能有连在一起的红色节点,此时需要对红黑树分情况来讨论:
约定:cur为当前节点,p为父节点,g为祖父节点,u为叔叔节点
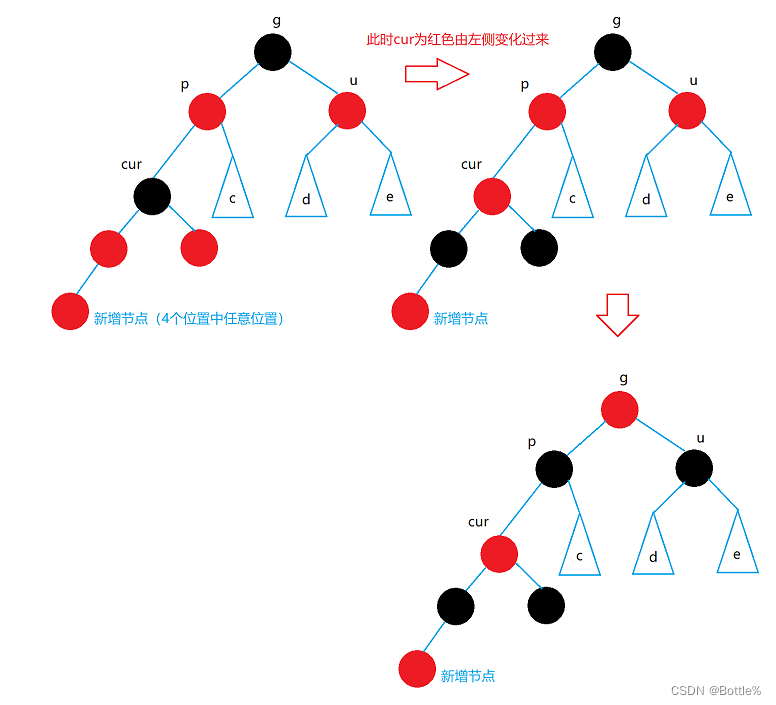
1.情况一:cur为红,p为红,g为黑,u存在且为红
解决方式:将p,u改为黑,g改为红,然后把g当成cur,继续向上调整。
(注意:下图中的树,可能是一颗完整二叉树,也可能是一颗子树)
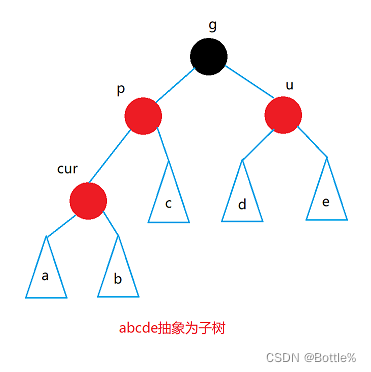

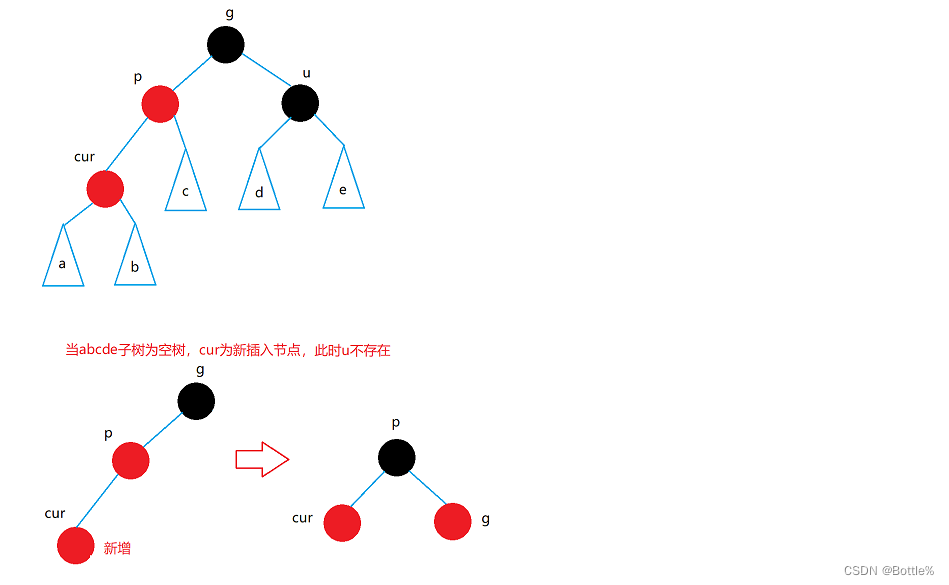
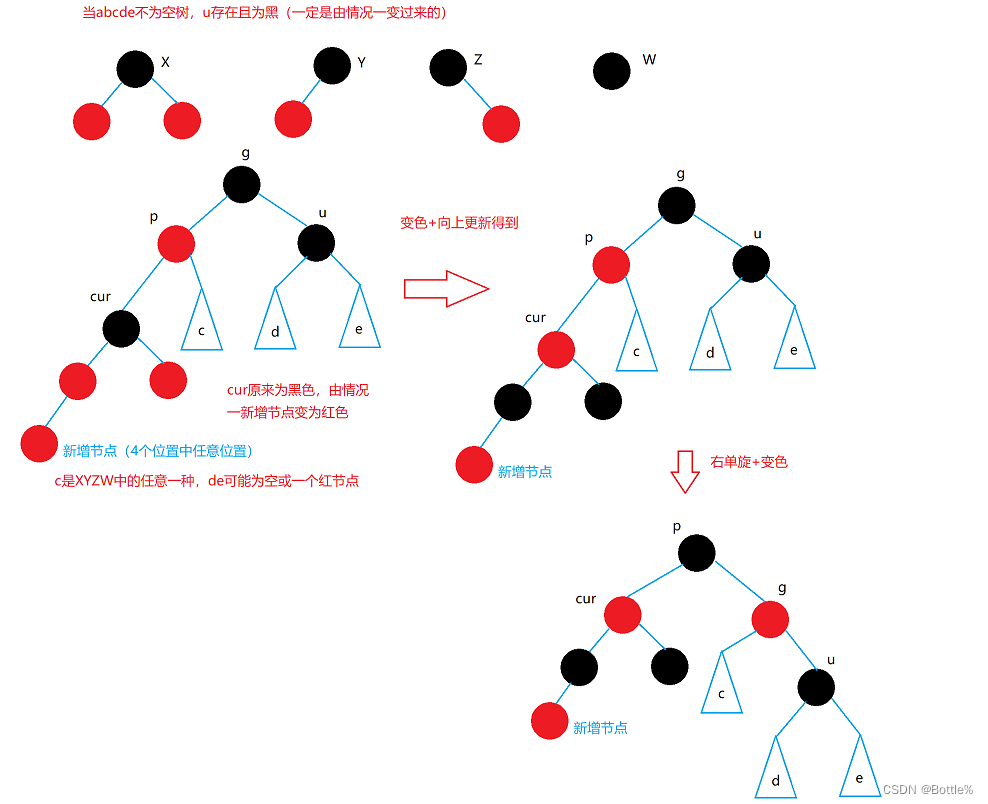
2.情况二: cur为红,p为红,g为黑,u不存在/u存在且为黑
解决方式:
- p为g的左孩子,cur为p的左孩子,则进行右单旋转;
- 相反, p为g的右孩子,cur为p的右孩子,则进行左单旋转
- p、g变色--p变黑,g变红
说明:u的情况有两种。
1. 如果u节点不存在,则cur一定是新插入节点,因为如果cur不是新插入节点,则cur和p一定有一个节点的颜色是黑色,就不满足性质4:每条路径黑色节点的数量相同。
2.如果u节点存在且黑色,那么cur节点原来的颜色一定是黑色,现在看到cur是红色的原因是因为cur的子树在调整过程中将cur节点的颜色由黑色变为红色。
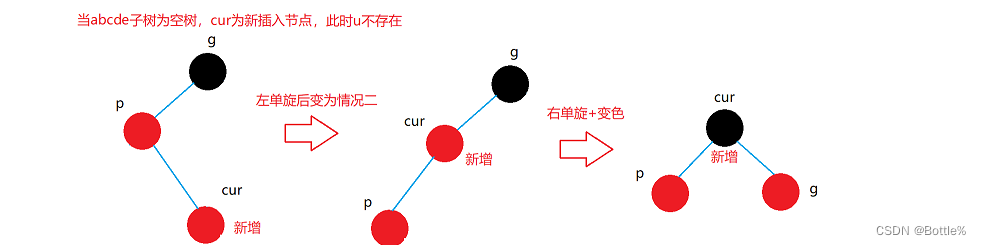
3.情况三: cur为红,p为红,g为黑,u不存在/u存在且为黑
解决方式:
- p为g的左孩子,cur为p的右孩子,则针对p做左单旋转;
- 相反, p为g的右孩子,cur为p的左孩子,则针对p做右单旋转,则转换成了情况2

其余情况都为上述情况的镜像,在此不做介绍了。
4.代码如下:
bool Insert(const pair<K, V>& kv)
{//寻找插入位置if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else{return false;}}cur = new Node(kv);cur->_parent = parent;if (parent->_kv.first > kv.first){parent->_left = cur;}else{parent->_right = cur;}//调整while (parent && parent->_col == RED){// 注意:grandfather一定存在// 因为parent存在,且不是黑色节点,则parent一定不是根,则其一定有双亲Node* grandfather = parent->_parent;// 先讨论左侧情况if ( grandfather->_left == parent){Node* uncle = grandfather->_right;if (uncle && uncle->_col == RED)// 情况1:u存在且为红,变色处理,并继续往上处理{parent->_col = BLACK;uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_parent;}else// 情况2+3:u不存在/u存在且为黑,旋转+变色{if (cur == parent->_left){RotateR(grandfather);//旋转部分代码见下文parent->_col = BLACK;grandfather->_col = RED;}else{RotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}else// 讨论右侧情况{Node* uncle = grandfather->_left;if (uncle && uncle->_col == RED)// 情况1:u存在且为红,变色处理,并继续往上处理{parent->_col = BLACK;uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_parent;}else// 情况2+3:u不存在/u存在且为黑,旋转+变色{if (cur == parent->_right){RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{RotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}//根节点变为黑色_root->_col = BLACK;return true;
}旋转部分:
void RotateL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;subR->_left = parent;Node* ppnode = parent->_parent;parent->_parent = subR;if (ppnode == nullptr){_root = subR;_root->_parent = nullptr;}else{subR->_parent = ppnode;if (ppnode->_left == parent){ppnode->_left = subR;}else{ppnode->_right = subR;}}
}void RotateR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;subL->_right = parent;Node* ppnode = parent->_parent;parent->_parent = subL;if (ppnode == nullptr){_root = subL;_root->_parent = nullptr;}else{subL->_parent = ppnode;if (ppnode->_left == parent){ppnode->_left = subL;}else{ppnode->_right = subL;}}
}红黑树的其他接口不做介绍了。
红黑树的删除
5.红黑树的验证
红黑树的检测分为两步:
- 检测其是否满足二叉搜索树(中序遍历是否为有序序列)
- 检测其是否满足红黑树的性质
bool _check(Node* root, int blackNum, int benchmark)
{if (root == nullptr){if (blackNum != benchmark){cout << "路径上黑色节点的数量不相等" << endl;return false;} }if (root->_col == BLACK)//记录路径中黑色节点的个数{++blackNum;}if (root->_col == RED && root->_parent->_col == RED){cout << "出现连续红色节点" << endl;return false;}//通过上方检测后递归判断左右子树return _check(root->_left, blackNum, benchmark)&& _check(root->_right, blackNum, benchmark);
}bool IsBalance()
{if (_root->_col == RED){cout << "根节点为红色" << endl;return false;}int benchmark = 0;Node* cur = _root;// 获取任意一条路径中黑色节点的个数,作为基准值while (cur){if(cur->_col == BLACK)++benchmark;cur = cur->_left;}return _check(_root, 0, benchmark);
}6.红黑树与AVL树的比较
红黑树和AVL树都是高效的平衡二叉树,增删改查的时间复杂度都是,红黑树不追求绝对平衡,其只需保证最长路径不超过最短路径的2倍,相对而言,降低了插入和旋转的次数, 所以在经常进行增删的结构中性能比AVL树更优,而且红黑树实现比较简单,所以实际运用中红黑树更多。
相关文章:
AVL树、红黑树的介绍和实现[C++]
本文主要对AVL树和红黑树的结构和实现方法进行一定的介绍,仅实现部分接口。 目录 一、AVL树 1.AVL树的概念 2.AVL树节点的定义 3.AVL树的插入 4.AVL树的旋转 1. 新节点插入较高左子树的左侧——左左:右单旋 2. 新节点插入较高右子树的右侧——右…...

meta分析的异质性检验指标如何计算?
一、什么是异质性? 广义:描述参与者、干预措施和一系列研究间测量结果的差异和多样性,或那些研究中内在真实性的变异。 狭义:统计学异质性,用来描述一系列研究中效应量的变异程度,也用于表明除仅可预见的…...

如何在mac 安装 cocos 的 android环境
基本概念: Java: Java 是一种编程语言,由Sun Microsystems(现在是 Oracle Corporation)开发。Java 是一种跨平台的语言,可以用于开发各种应用程序,包括 Android 应用程序。Android 应用程序的核心代码通常用…...

作为网工有必要了解一下什么是SRv6?
什么是SRv6? 【微|信|公|众|号:厦门微思网络】 【微思网络http://www.xmws.cn,成立于2002年,专业培训21年,思科、华为、红帽、ORACLE、VMware等厂商认证及考试,以及其他认证PMP、CISP、ITIL等】 SRv6&…...

Jmeter(十八):硬件性能监控指标详解
硬件性能监控指标 一、性能监控初步介绍 性能测试的主要目标 1.在当前的服务器配置情况,最大的用户数 2.平均响应时间ART,找出时间较长的业务 3.每秒事务数TPS,服务器的处理能力 性能测试涉及的内容 1.客户端性能测试:web前…...

【ARM Trace32(劳特巴赫) 使用介绍 2 -- Trace32 cmm 脚本基本语法及常用命令】
文章目录 Trace32 CMM 概述1.1 Trace32 系统命令 SYStem1.1.1 Trace32 SYStem.CONFIG1.1.2 SYStem.MemAccess1.1.3 SYStem.Mode1.1.3.1 TRST-Resets the JTAG TAP controller and the CPU internal debug logic1.1.3.2 SRST- Resets the CPU core and peripherals 1.2 Trace32 …...

2023年第七期丨全国高校大数据与人工智能师资研修班
全国高校大数据与人工智能 师资研修班邀请函 2023年第七期 线下班(昆明): 数据采集与机器学习实战 线上班(七大专题): PyTorch深度学习与大模型应用实战 数据采集与处理实战 大数据分析与机器学习实战 大数据技…...
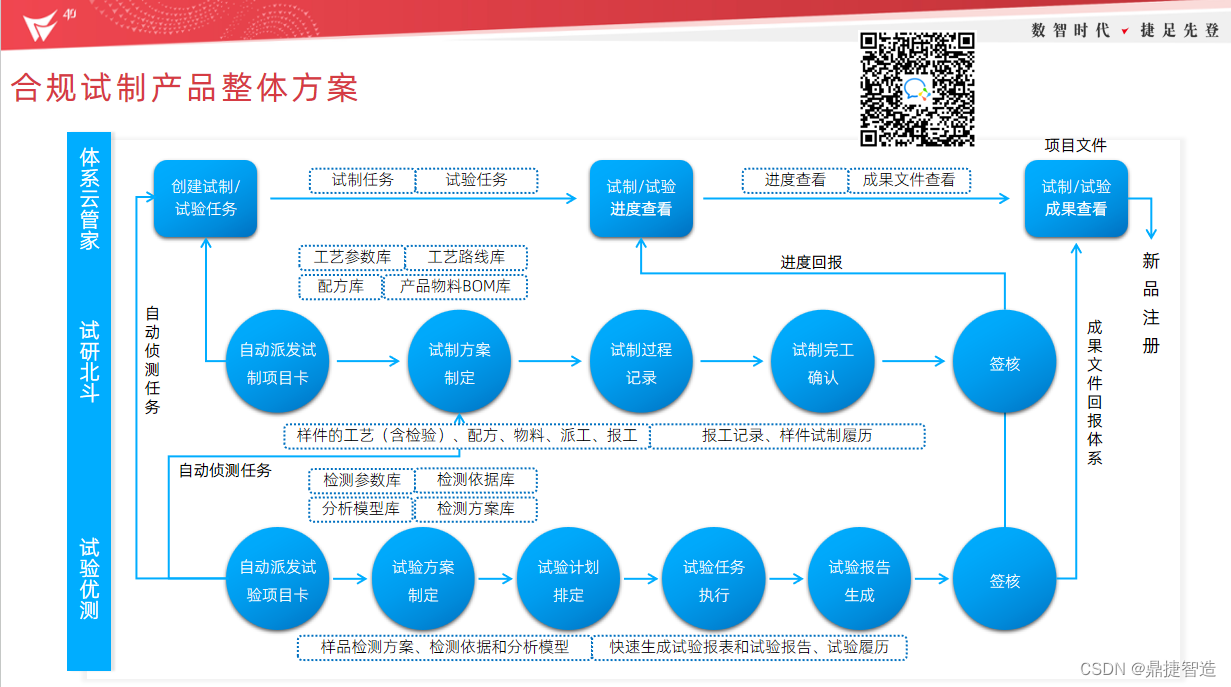
一文获取鼎捷医疗器械行业数智化合规敏态方案
医疗器械产业是关乎国计民生的重要产业,高端医疗器械更是“国之重器”。为加强医疗器械的监督管理,提升行业质量和安全整体水平,我国出台了《医疗器械监督管理条例》、《医疗器械召回管理办法》、《医疗器械临床试验质量管理规范》、《医疗器…...

2023最新版本 FreeRTOS教程 -1-标准库移植FreeRTOS
源码下载 官网下载驱动 点击直达 源码剪裁 剪裁之后的图片,找我免费获取 添加进MDK 配置滴答定时器 全部工程获取 查看下方头像...
)
python笔记(函数参数、面向对象、装饰器、高级函数、捕获异常)
Python 笔记 函数参数 默认参数 在Python中,我们可以为函数的参数设置默认值。如果调用函数时没有传递参数,那么参数将使用默认值。 def greet(nameWorld):print(f"Hello, {name}!")greet() # 输出:Hello, World! greet…...

JAVA命令总结
jps命令的基本语法如下: jps [options] [hostid]其中,options是可选参数,用于指定额外的选项,hostid是可选参数,用于指定在远程主机上执行jps命令。 以下是一些常用的jps命令选项: -q:仅显示…...
删除的PPT怎么找回来?4个必备恢复方法!
“最近的期末展示需要制作一个PPT,我熬了几个大夜才完成了,但是不知道怎么的我在删除其他文件时不小心把这个PPT一起删掉了,有什么方法可以帮我找回这个误删的PPT吗?” 我们在工作和学习中,经常都需要使用到PPT&#x…...
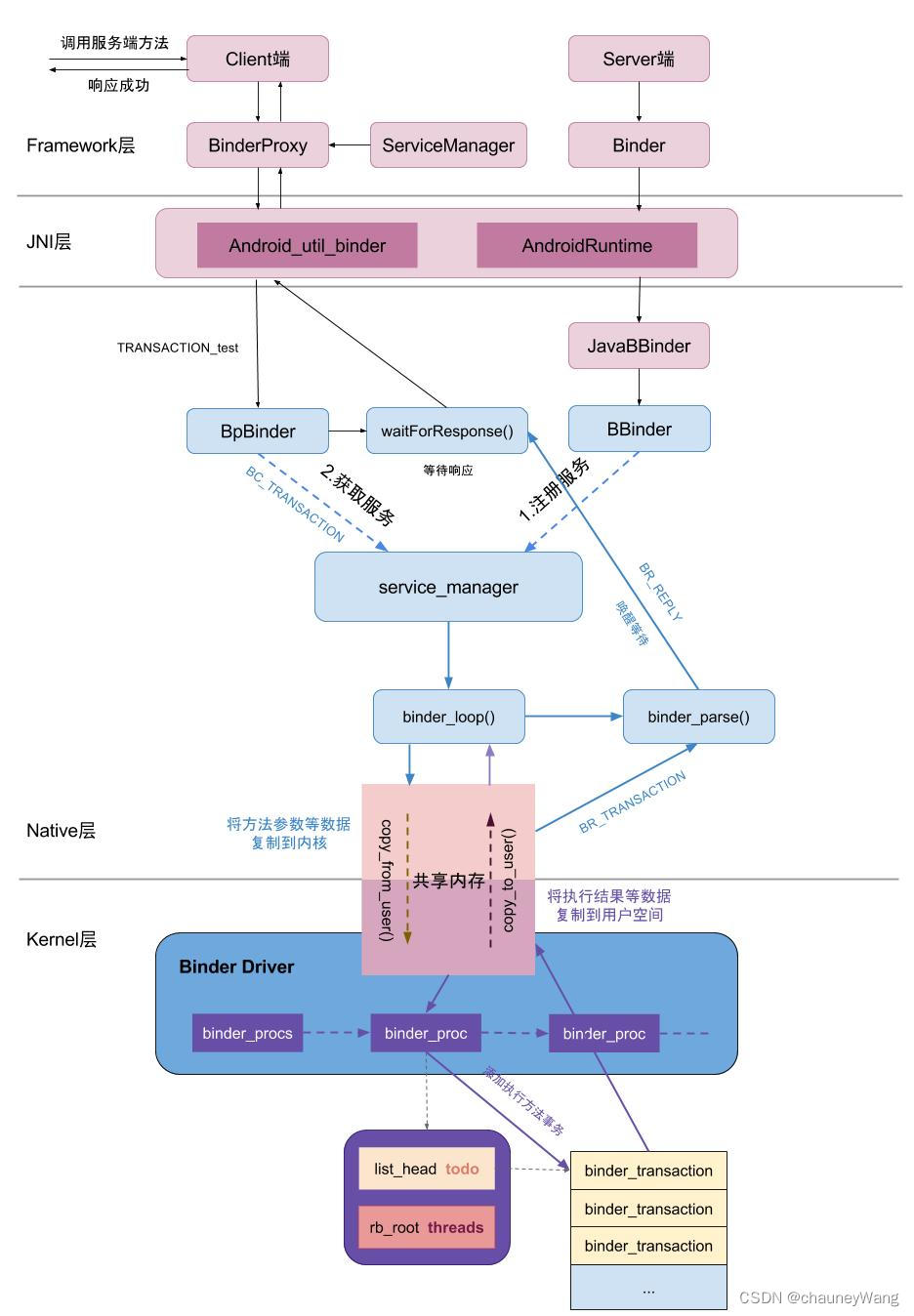
Binder机制总结笔记
Binder机制总结笔记 什么是Binder? Binder的Android特有的IPC通信机制。Android的四大组件Activity、Service、Broadcast、ContentProvider,不同的App等都运行在不同的进程内,他们之间的通信都需要依靠Binder完成。因此Binder在整个Android系…...
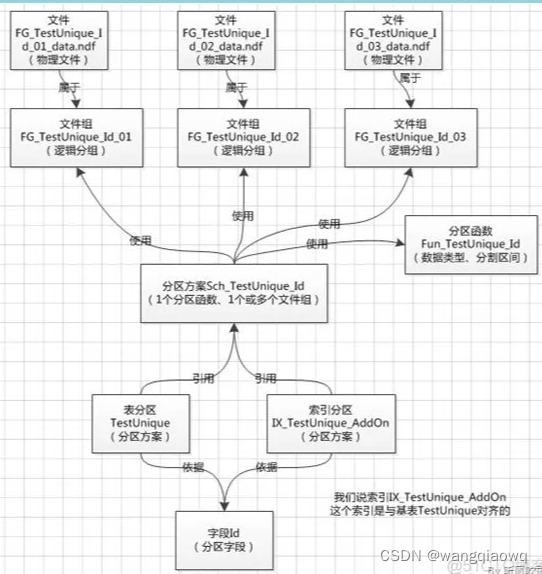
SQL SERVER 表分区
1. 概要说明 SQL SERVER的表分区功能是为了将一个大表(表中含有非常多条数据)的数据根据某条件(仅限该表的主键)拆分成多个文件存放,以提高查询数据时的效率。创建表分区的主要步骤是 1、确定需要以哪一个字段作为分…...
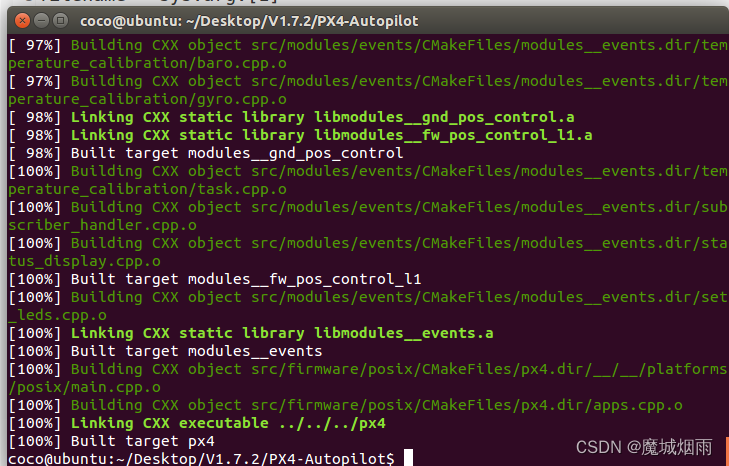
从零开始学习PX4源码0(固件下载及编译)
目录 文章目录目录摘要1.重点学习网址2.固件下载1.下载最新版本固件2.下载之前版本固件 摘要 本节主要记录从零开始学习PX4源码1(固件下载)的过程,欢迎批评指正!!! 下载固件主要分为两个版本,之前稳定版本和最新官网发布版本,为什么要下载两个版本,主要是说明两个版本有…...

centos格式化硬盘/u盘的分区为NTFS格式
centos7好像不支持ntfs? 对报这个,ntfs not configured in kernel。 安装了ntfs-3g就可以访问了。 插上u盘查看u盘设备 #查看硬件设备及挂载目录 df -h #查看硬件设备(包括未挂载的) fdisk -l卸载外部设备 umount /dev/sdbxxx …...

【工具】FreePic2PDF+PdgCntEditor|PDF批量添加书签(Windows)
这俩软件都不大,比较便携。 FreePic2PDF: 我下载的来源:https://www.52pojie.cn/thread-1317140-1-1.html(包含下载链接https://www.lanzoui.com/it4x6j4hbvc)下载的结果:https://pan.baidu.com/s/1r8n5G42…...
中移链浏览器简介
(1)简介 生活中,常用的互联网浏览器,是用来检索、展示以及传递Web信息资源的应用程序。用浏览器进行搜索,可以快速查找到目标信息。而对于区块链而言,也有区块链浏览器。 区块链浏览器,是指为用…...
深入浅出排序算法之计数排序
目录 1. 原理 2. 代码实现 3. 性能分析 1. 原理 首先看一个题目,有n个数,取值范围是 0~n,写出一个排序算法,要求时间复杂度和空间复杂度都是O(n)的。 为了达到这种效果,这一篇将会介绍一种不基于比较的排序方法。这…...

大坝水库安全监测终端MCU,智能化管理的新篇章!
我国目前拥有超过9.8万座水库大坝,其中超过95%为土石坝,这些大坝主要是在上世纪80年代以前建造的。这些水库大坝在保障防洪、发电、供水、灌溉等方面发挥了巨大的作用,但是同时也存在一定的安全风险,比如坝体结构破损、坝基渗漏、…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...
