leetcode第369周赛
2917. 找出数组中的 K-or 值
给你一个下标从 0 开始的整数数组 nums 和一个整数 k 。
nums 中的 K-or 是一个满足以下条件的非负整数:
- 只有在
nums中,至少存在k个元素的第i位值为 1 ,那么 K-or 中的第i位的值才是 1 。
返回 nums 的 K-or 值。
注意 :对于整数 x ,如果 (2^i AND x) == 2^i ,则 x 中的第 i 位值为 1 ,其中 AND 为按位与运算符。
示例 1:
输入:nums = [7,12,9,8,9,15], k = 4 输出:9 解释:nums[0]、nums[2]、nums[4] 和 nums[5] 的第 0 位的值为 1 。 nums[0] 和 nums[5] 的第 1 位的值为 1 。 nums[0]、nums[1] 和 nums[5] 的第 2 位的值为 1 。 nums[1]、nums[2]、nums[3]、nums[4] 和 nums[5] 的第 3 位的值为 1 。 只有第 0 位和第 3 位满足数组中至少存在 k 个元素在对应位上的值为 1 。因此,答案为 2^0 + 2^3 = 9 。
示例 2:
输入:nums = [2,12,1,11,4,5], k = 6 输出:0 解释:因为 k == 6 == nums.length ,所以数组的 6-or 等于其中所有元素按位与运算的结果。因此,答案为 2 AND 12 AND 1 AND 11 AND 4 AND 5 = 0 。
示例 3:
输入:nums = [10,8,5,9,11,6,8], k = 1 输出:15 解释:因为 k == 1 ,数组的 1-or 等于其中所有元素按位或运算的结果。因此,答案为 10 OR 8 OR 5 OR 9 OR 11 OR 6 OR 8 = 15 。
提示:
1 <= nums.length <= 500 <= nums[i] < 2^311 <= k <= nums.length
思路:
简单题目,直接遍历就好了。
最多只有31位,而且数组长度也才50。重点是 (2^i AND x) == 2^i
两层遍历,外层范围[0-31],内层范围[0-n],n是数组的长度。
ac code:
class Solution {public int findKOr(int[] nums, int k) {int ans = 0;for (int j=0;j<31;j++) {int cnt = 0;for (int num : nums) {if ((num & (1 << j)) == (1 << j)) {cnt += 1;}if (cnt >= k) {ans = ans + (1 << j);break;}}}return ans;}
}2918. 数组的最小相等和
给你两个由正整数和 0 组成的数组 nums1 和 nums2 。
你必须将两个数组中的 所有 0 替换为 严格 正整数,并且满足两个数组中所有元素的和 相等 。
返回 最小 相等和 ,如果无法使两数组相等,则返回 -1 。
示例 1:
输入:nums1 = [3,2,0,1,0], nums2 = [6,5,0] 输出:12 解释:可以按下述方式替换数组中的 0 : - 用 2 和 4 替换 nums1 中的两个 0 。得到 nums1 = [3,2,2,1,4] 。 - 用 1 替换 nums2 中的一个 0 。得到 nums2 = [6,5,1] 。 两个数组的元素和相等,都等于 12 。可以证明这是可以获得的最小相等和。
示例 2:
输入:nums1 = [2,0,2,0], nums2 = [1,4] 输出:-1 解释:无法使两个数组的和相等。
提示:
1 <= nums1.length, nums2.length <= 10^50 <= nums1[i], nums2[i] <= 10^6
思路:
直接模拟。答案分几种情况,只要捋清楚即可。
1、nums1不存在0:
1)nums2不存在0:
value1(nums1的sum值,同下)!= value2(nums2的sum值,同下)那么就return -1
2)nums2存在0:
value1 <= (value2+cnt2(代表nums2种0的个数,同下)):因为0是严格替换成了正整数,那么最小也是1,已经比value1还要大了,再加上正整数,不可能使得value2变小,所以,return -1 ;
value1 > value 2:因为可以换成任意正整数,所以,value2肯定可以变大成任意值。那么最小的话,肯定就是value1,所以return value1即可。
2、nums1存在0:
1)nums2 不存在0:
同理,(value1 + cnt1) >= value2 即可return -1;
value1 < value2,则 return value2
2)nums2 存在0:
因为0最小也是换成1,所以value的范围其实是可以确定的。例如nums1值的范围是[value1 + cnt1(nums1存在0的个数), 正无穷)
那么nums2也是同理。所以,返回的值取范围交集即可。return Math.max(value1+cnt1, value2+cnt2),为什么是max呢?因为交集!!! 不懂得可以画个图,或者举几个例子。
捋清楚之后,按照分类写清楚就行( 之前没捋清楚还wa了一次。。。)
具体细节,看代码
ac code
class Solution {public long minSum(int[] nums1, int[] nums2) {long value1 = 0; // nums1的sumlong value2 = 0; // nums2的sumint cnt1 = 0; // num1的0的个数int cnt2 = 0; // num2的0的个数for (int num : nums1) {if (num == 0) {cnt1 += 1;}value1 += num;}for (int num : nums2) {if (num == 0) {cnt2 += 1;}value2 += num;}// 需要判断value1 如果小于 value2 + cnt2,那么无论如何都不可能if (cnt1 == 0 && value1 <= (value2+cnt2)) {if (cnt2 == 0 && value1 == value2) {return value1;} else if (value1 == (value2+cnt2)) {return value1;}return -1;}if (cnt2 == 0 && value2 <= (value1+cnt1)) {if (cnt1 == 0 && value1 == value2) {return value1;} else if (value2 == (value1+cnt1)) {return value2;}return -1;}if (cnt1 == 0) {return value1;}if (cnt2 == 0) {return value2;}return Math.max(value1+cnt1, value2+cnt2); }
}2919. 使数组变美的最小增量运算数
给你一个下标从 0 开始、长度为 n 的整数数组 nums ,和一个整数 k 。
你可以执行下述 递增 运算 任意 次(可以是 0 次):
- 从范围
[0, n - 1]中选择一个下标i,并将nums[i]的值加1。
如果数组中任何长度 大于或等于 3 的子数组,其 最大 元素都大于或等于 k ,则认为数组是一个 美丽数组 。
以整数形式返回使数组变为 美丽数组 需要执行的 最小 递增运算数。
子数组是数组中的一个连续 非空 元素序列。
示例 1:
输入:nums = [2,3,0,0,2], k = 4 输出:3 解释:可以执行下述递增运算,使 nums 变为美丽数组: 选择下标 i = 1 ,并且将 nums[1] 的值加 1 -> [2,4,0,0,2] 。 选择下标 i = 4 ,并且将 nums[4] 的值加 1 -> [2,4,0,0,3] 。 选择下标 i = 4 ,并且将 nums[4] 的值加 1 -> [2,4,0,0,4] 。 长度大于或等于 3 的子数组为 [2,4,0], [4,0,0], [0,0,4], [2,4,0,0], [4,0,0,4], [2,4,0,0,4] 。 在所有子数组中,最大元素都等于 k = 4 ,所以 nums 现在是美丽数组。 可以证明无法用少于 3 次递增运算使 nums 变为美丽数组。 因此,答案为 3 。
示例 2:
输入:nums = [0,1,3,3], k = 5 输出:2 解释:可以执行下述递增运算,使 nums 变为美丽数组: 选择下标 i = 2 ,并且将 nums[2] 的值加 1 -> [0,1,4,3] 。 选择下标 i = 2 ,并且将 nums[2] 的值加 1 -> [0,1,5,3] 。 长度大于或等于 3 的子数组为 [0,1,5]、[1,5,3]、[0,1,5,3] 。 在所有子数组中,最大元素都等于 k = 5 ,所以 nums 现在是美丽数组。 可以证明无法用少于 2 次递增运算使 nums 变为美丽数组。 因此,答案为 2 。
示例 3:
输入:nums = [1,1,2], k = 1 输出:0 解释:在这个示例中,只有一个长度大于或等于 3 的子数组 [1,1,2] 。 其最大元素 2 已经大于 k = 1 ,所以无需执行任何增量运算。 因此,答案为 0 。
提示:
3 <= n == nums.length <= 10^50 <= nums[i] <= 10^90 <= k <= 10^9
思路:
挺有意思的一道题目,算是益智题了。一开始想到的是滑动窗口,最小长度3,然后将窗口内最大值进行增大到k值,后来发现不对,因为窗口内最大值并不一定是最优的,那么就会希望有一个后悔的操作,比如增大了a,但是发现不是最优的,想要增大相邻的b。如何“后悔”增大某个数字?
举个例子:
[43,31,14,4]
73
如果按照原本的想法,增大窗口内最大值,窗口长度是3。那么应该增大43,然后窗口向右滑动后,没有满足条件的k值,则增大31到k值。这样发现,一共花费了30 + 42 = 62。
但是如果我们仅仅只增大31呢? 那么其实就只需要花费42即可。
此时,我们可以考虑下,如果我们选择了43的时候,如果后续需要后悔,那么对于相邻的31是不是需要进行变大操作。
一步步来看:([xxx]表示窗口)
[43,31,14],4
经过操作 假设先按照之前的贪心的想法,先把43进行变动为
[73,31,14],4
此时我们已经花费了30了,如果只是单纯将31 -> 73 是需要42,目前已经花费了30,那么就还需要12,所以,我们可以将31同步转换为61,同理14同步转换为44,即
[73,61,44],4
所以在下一个窗口后那么就是:
73,[61,44,4]
这个时候我们就只需要花费12 就可以满足条件,这样相当于就是执行了后悔的操作。是不是很巧妙的一个办法。
而且,我们还需要注意,窗口尽可能往后取值。
具体实现细节可以看看代码。
ac code
class Solution {public long minIncrementOperations(int[] nums, int k) {int first = nums[0];int second = nums[1];int third = nums[2];int n = nums.length;long ans = 0;// 窗口长度为3for (int i=3;i<=n;i++) {// 如果没有满足条件的值才需要进行变换if (first < k && second < k && third < k) {// 找到最大值int tmp = Math.max(first, Math.max(second, third));ans += (k - tmp); // 计算代价if (third == tmp) { // 如果是最后一个的话,直接变就行,因为它在窗口待最久third = k;} else if (second == tmp) { // 如果是第二个,只需要把后面的加上后悔操作即可,毕竟第一个马上要出窗口了second = k;third += (k - tmp);} else { // 同上first = k;second += (k - tmp);third += (k - tmp);}}// 窗口向右滑动if (i < n) {first = second;second = third;third = nums[i];}}return ans;}
}2920. 收集所有金币可获得的最大积分
节点 0 处现有一棵由 n 个节点组成的无向树,节点编号从 0 到 n - 1 。给你一个长度为 n - 1 的二维 整数 数组 edges ,其中 edges[i] = [ai, bi] 表示在树上的节点 ai 和 bi 之间存在一条边。另给你一个下标从 0 开始、长度为 n 的数组 coins 和一个整数 k ,其中 coins[i] 表示节点 i 处的金币数量。
从根节点开始,你必须收集所有金币。要想收集节点上的金币,必须先收集该节点的祖先节点上的金币。
节点 i 上的金币可以用下述方法之一进行收集:
- 收集所有金币,得到共计
coins[i] - k点积分。如果coins[i] - k是负数,你将会失去abs(coins[i] - k)点积分。 - 收集所有金币,得到共计
floor(coins[i] / 2)点积分。如果采用这种方法,节点i子树中所有节点j的金币数coins[j]将会减少至floor(coins[j] / 2)。
返回收集 所有 树节点的金币之后可以获得的最大积分。
示例 1:

输入:edges = [[0,1],[1,2],[2,3]], coins = [10,10,3,3], k = 5
输出:11
解释:
使用第一种方法收集节点 0 上的所有金币。总积分 = 10 - 5 = 5 。
使用第一种方法收集节点 1 上的所有金币。总积分 = 5 + (10 - 5) = 10 。
使用第二种方法收集节点 2 上的所有金币。所以节点 3 上的金币将会变为 floor(3 / 2) = 1 ,总积分 = 10 + floor(3 / 2) = 11 。
使用第二种方法收集节点 3 上的所有金币。总积分 = 11 + floor(1 / 2) = 11.
可以证明收集所有节点上的金币能获得的最大积分是 11 。
示例 2:
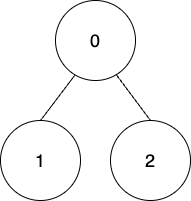
输入:edges = [[0,1],[0,2]], coins = [8,4,4], k = 0
输出:16
解释:
使用第一种方法收集所有节点上的金币,因此,总积分 = (8 - 0) + (4 - 0) + (4 - 0) = 16 。
提示:
n == coins.length2 <= n <= 10^50 <= coins[i] <= 10^4edges.length == n - 10 <= edges[i][0], edges[i][1] < n0 <= k <= 10^4
思路:
树上dp,不太会。。。 放下别人的题解。。。
把 floor(coins[i] / 2) 看成右移操作。
一个数最多右移多少次,就变成 000 了?在本题的数据范围下,这至多是 141414 次。
同时,右移操作是可以叠加的,我们可以记录子树中的节点值右移了多少次。
所以可以定义 dfs(i,j)\textit{dfs}(i,j)dfs(i,j) 表示子树 iii 在已经右移 jjj 次的前提下,最多可以得到多少积分。
用「选或不选」来思考,即是否右移:
不右移:答案为 (coins[i]>>j)−k(\textit{coins}[i]>>j)-k(coins[i]>>j)−k 加上每个子树 ch\textit{ch}ch 的 dfs(ch,j)\textit{dfs}(ch,j)dfs(ch,j)。
右移:答案为 coins[i]>>(j+1)\textit{coins}[i]>>(j+1)coins[i]>>(j+1) 加上每个子树 ch\textit{ch}ch 的 dfs(ch,j+1)\textit{dfs}(ch,j+1)dfs(ch,j+1)。
这两种情况取最大值。
作者:灵茶山艾府
class Solution {public int maximumPoints(int[][] edges, int[] coins, int k) {int n = coins.length;List<Integer>[] g = new ArrayList[n];Arrays.setAll(g, e -> new ArrayList<>());for (int[] e : edges) {int x = e[0], y = e[1];g[x].add(y);g[y].add(x);}int[][] memo = new int[n][14];for (int[] m : memo) {Arrays.fill(m, -1); // -1 表示没有计算过}return dfs(0, 0, -1, memo, g, coins, k);}private int dfs(int i, int j, int fa, int[][] memo, List<Integer>[] g, int[] coins, int k) {if (memo[i][j] != -1) { // 之前计算过return memo[i][j];}int res1 = (coins[i] >> j) - k;int res2 = coins[i] >> (j + 1);for (int ch : g[i]) {if (ch == fa) continue;res1 += dfs(ch, j, i, memo, g, coins, k); // 不右移if (j < 13) { // j+1 >= 14 相当于 res2 += 0,无需递归res2 += dfs(ch, j + 1, i, memo, g, coins, k); // 右移}}return memo[i][j] = Math.max(res1, res2); // 记忆化}
}相关文章:

leetcode第369周赛
2917. 找出数组中的 K-or 值 给你一个下标从 0 开始的整数数组 nums 和一个整数 k 。 nums 中的 K-or 是一个满足以下条件的非负整数: 只有在 nums 中,至少存在 k 个元素的第 i 位值为 1 ,那么 K-or 中的第 i 位的值才是 1 。 返回 nums …...

如何在维格云中自动新增一行或多行数据?
简介 在日常使用维格云中,通常会出现一张表中有数据发生变化时,需要另一张表同时新增一些数据,比如: 项目管理中,每新增一个项目,都要在任务表中产生若干个固定的任务;或一个任务要自动生成若干子任务当一笔订单状态变为成交后,可能要在客户成功表中新增一行记录;帮…...
Three.js 开发引擎的特点
Three.js 是一个流行的开源 3D 游戏和图形引擎,用于在 Web 浏览器中创建高质量的三维图形和互动内容。以下是 Three.js 的主要特点和适用场合,希望对大家有所帮助。北京木奇移动技术有限公司,专业的软件外包开发公司,欢迎交流合作…...

k8s声明式资源管理方式
Kubernetes 支持 YAML 和 JSON 格式管理资源对象 JSON 格式:主要用于 api 接口之间消息的传递 YAML 格式:用于配置和管理,YAML 是一种简洁的非标记性语言,内容格式人性化,较易读 YAML 语法格式: ●大小写…...
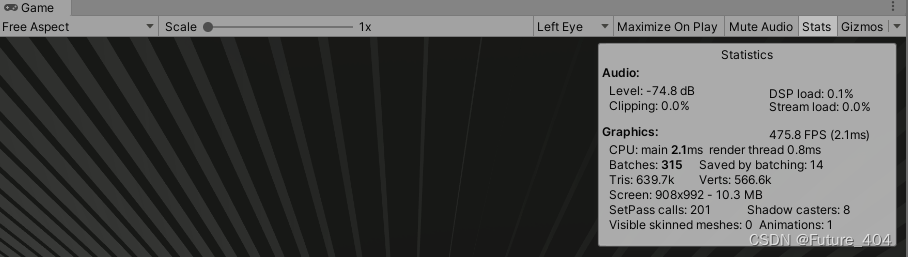
unity性能优化__Statistic状态分析
在Unity的Game视图右上角,我们会看到有Stats选项,点击会出现这样的信息 我使用的Unity版本是2019.4.16 一、Audio,顾名思义是声音信息 1:Level:-74.8dB 声音的相对强度或音量。通常,音量级别以分贝(dB&a…...
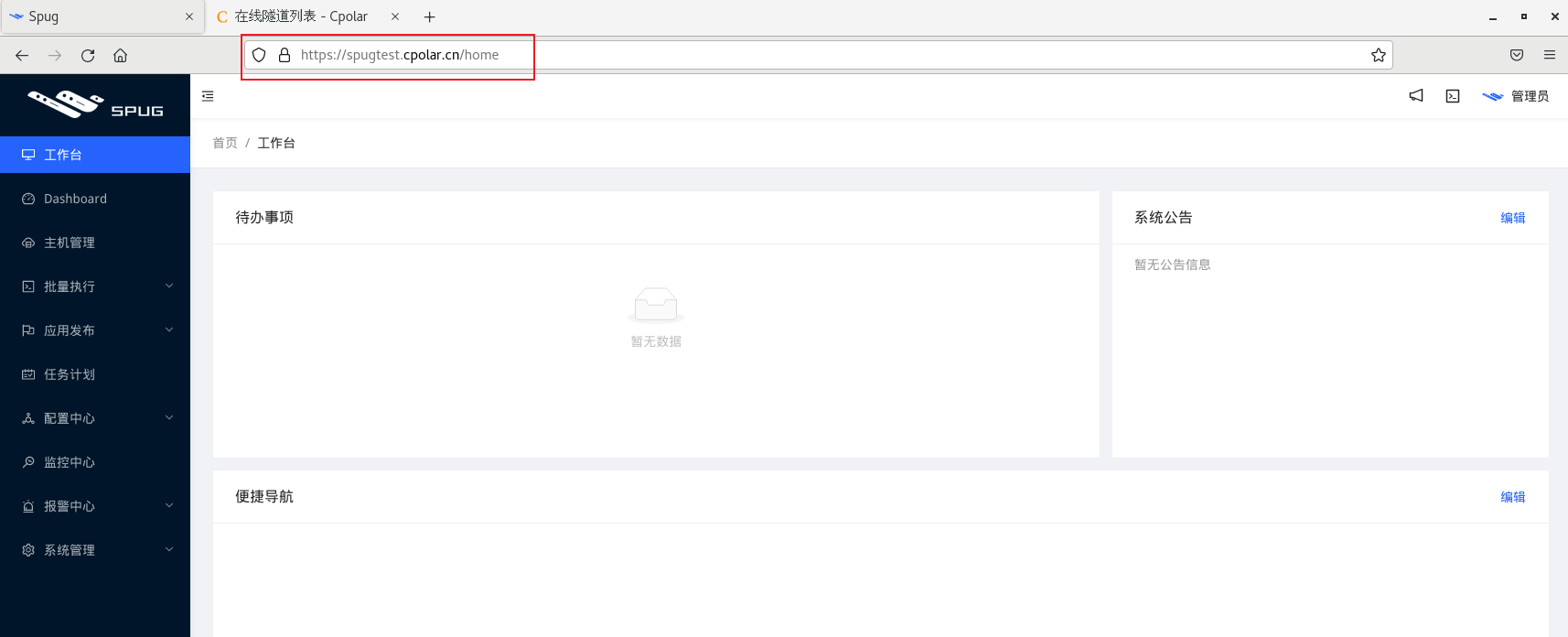
Linux Spug自动化运维平台公网远程访问
文章目录 前言1. Docker安装Spug2 . 本地访问测试3. Linux 安装cpolar4. 配置Spug公网访问地址5. 公网远程访问Spug管理界面6. 固定Spug公网地址 前言 Spug 面向中小型企业设计的轻量级无 Agent 的自动化运维平台,整合了主机管理、主机批量执行、主机在线终端、文件…...

3DES算法
简介 本文基于.NET的C#实现3DES算法的加密和解密过程。可以用在加密软件、加密狗等。 代码下载链接:https://download.csdn.net/download/C_gyl/88487942 使用 第一种方法 加密 KeySize:128(16字节),192(24字节&#x…...

手机电池寿命检测
安卓 - 应用商店下载“安兔兔” -accubattery 下载地址 accubattery汉化版下载-Accubattery pro中文免费版(电池检测)下载 v1.5.11 安卓专业版-IT猫扑网...
Vue项目搭建及使用vue-cli创建项目、创建登录页面、与后台进行交互,以及安装和使用axios、qs和vue-axios
目录 1. 搭建项目 1.1 使用vue-cli创建项目 1.2 通过npm安装element-ui 1.3 导入组件 2 创建登录页面 2.1 创建登录组件 2.2 引入css(css.txt) 2.3 配置路由 2.5 运行效果 3. 后台交互 3.1 引入axios 3.2 axios/qs/vue-axios安装与使用 3.2…...
AVL树、红黑树的介绍和实现[C++]
本文主要对AVL树和红黑树的结构和实现方法进行一定的介绍,仅实现部分接口。 目录 一、AVL树 1.AVL树的概念 2.AVL树节点的定义 3.AVL树的插入 4.AVL树的旋转 1. 新节点插入较高左子树的左侧——左左:右单旋 2. 新节点插入较高右子树的右侧——右…...

meta分析的异质性检验指标如何计算?
一、什么是异质性? 广义:描述参与者、干预措施和一系列研究间测量结果的差异和多样性,或那些研究中内在真实性的变异。 狭义:统计学异质性,用来描述一系列研究中效应量的变异程度,也用于表明除仅可预见的…...

如何在mac 安装 cocos 的 android环境
基本概念: Java: Java 是一种编程语言,由Sun Microsystems(现在是 Oracle Corporation)开发。Java 是一种跨平台的语言,可以用于开发各种应用程序,包括 Android 应用程序。Android 应用程序的核心代码通常用…...

作为网工有必要了解一下什么是SRv6?
什么是SRv6? 【微|信|公|众|号:厦门微思网络】 【微思网络http://www.xmws.cn,成立于2002年,专业培训21年,思科、华为、红帽、ORACLE、VMware等厂商认证及考试,以及其他认证PMP、CISP、ITIL等】 SRv6&…...

Jmeter(十八):硬件性能监控指标详解
硬件性能监控指标 一、性能监控初步介绍 性能测试的主要目标 1.在当前的服务器配置情况,最大的用户数 2.平均响应时间ART,找出时间较长的业务 3.每秒事务数TPS,服务器的处理能力 性能测试涉及的内容 1.客户端性能测试:web前…...

【ARM Trace32(劳特巴赫) 使用介绍 2 -- Trace32 cmm 脚本基本语法及常用命令】
文章目录 Trace32 CMM 概述1.1 Trace32 系统命令 SYStem1.1.1 Trace32 SYStem.CONFIG1.1.2 SYStem.MemAccess1.1.3 SYStem.Mode1.1.3.1 TRST-Resets the JTAG TAP controller and the CPU internal debug logic1.1.3.2 SRST- Resets the CPU core and peripherals 1.2 Trace32 …...

2023年第七期丨全国高校大数据与人工智能师资研修班
全国高校大数据与人工智能 师资研修班邀请函 2023年第七期 线下班(昆明): 数据采集与机器学习实战 线上班(七大专题): PyTorch深度学习与大模型应用实战 数据采集与处理实战 大数据分析与机器学习实战 大数据技…...
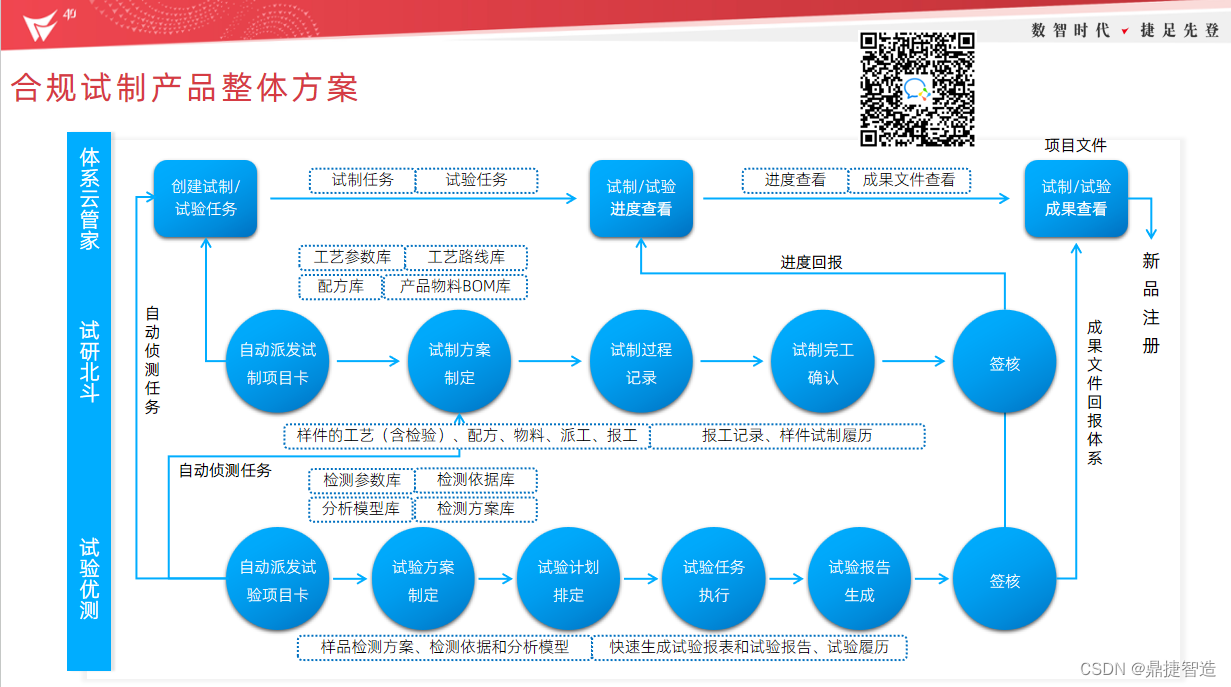
一文获取鼎捷医疗器械行业数智化合规敏态方案
医疗器械产业是关乎国计民生的重要产业,高端医疗器械更是“国之重器”。为加强医疗器械的监督管理,提升行业质量和安全整体水平,我国出台了《医疗器械监督管理条例》、《医疗器械召回管理办法》、《医疗器械临床试验质量管理规范》、《医疗器…...

2023最新版本 FreeRTOS教程 -1-标准库移植FreeRTOS
源码下载 官网下载驱动 点击直达 源码剪裁 剪裁之后的图片,找我免费获取 添加进MDK 配置滴答定时器 全部工程获取 查看下方头像...
)
python笔记(函数参数、面向对象、装饰器、高级函数、捕获异常)
Python 笔记 函数参数 默认参数 在Python中,我们可以为函数的参数设置默认值。如果调用函数时没有传递参数,那么参数将使用默认值。 def greet(nameWorld):print(f"Hello, {name}!")greet() # 输出:Hello, World! greet…...

JAVA命令总结
jps命令的基本语法如下: jps [options] [hostid]其中,options是可选参数,用于指定额外的选项,hostid是可选参数,用于指定在远程主机上执行jps命令。 以下是一些常用的jps命令选项: -q:仅显示…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...
