堆的基本存储
一、概念及其介绍
堆(Heap)是计算机科学中一类特殊的数据结构的统称。
堆通常是一个可以被看做一棵完全二叉树的数组对象。
堆满足下列性质:
堆中某个节点的值总是不大于或不小于其父节点的值。
堆总是一棵完全二叉树。
二、适用说明
堆是利用完全二叉树的结构来维护一组数据,然后进行相关操作,一般的操作进行一次的时间复杂度在 O(1)~O(logn) 之间,堆通常用于动态分配和释放程序所使用的对象。
若为优先队列的使用场景,普通数组或者顺序数组,最差情况为 O(n^2),堆这种数据结构也可以提高入队和出队的效率。
入队 | 出队 | |
普通数组 | O(1) | O(n) |
顺序数组 | O(n) | O(1) |
堆 | O(logn) | O(log) |
三、结构图示
二叉堆是一颗完全二叉树,且堆中某个节点的值总是不大于其父节点的值,该完全二叉树的深度为 k,除第 k 层外,其它各层 (1~k-1) 的结点数都达到最大个数,第k 层所有的结点都连续集中在最左边。
其中堆的根节点最大称为最大堆,如下图所示:

我们可以使用数组存储二叉堆,右边的标号是数组的索引。
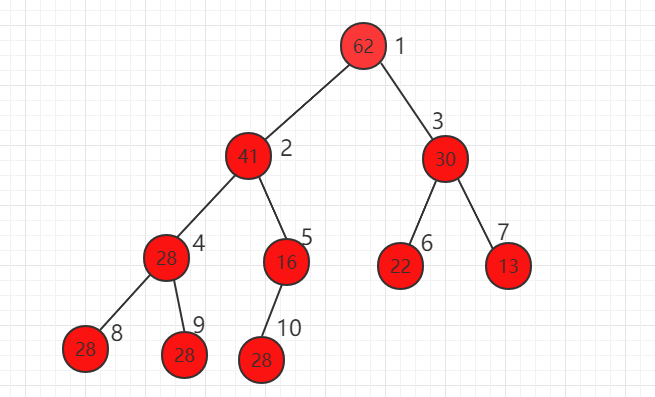
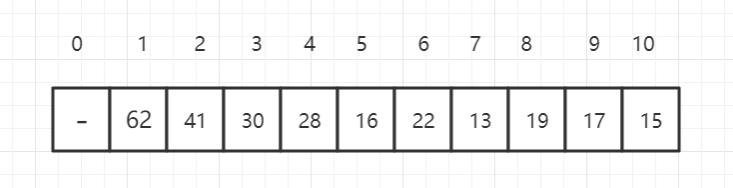
假设当前元素的索引位置为 i,可以得到规律:
parent(i) = i/2(取整)
left child(i) = 2*i
right child(i) = 2*i +1
四、Java 实例代码
src/runoob/heap/MaxHeap.java 文件代码:
package runoob.heap;/*** 堆定义*/
public class MaxHeap<T> {private T[] data;private int count;// 构造函数, 构造一个空堆, 可容纳capacity个元素public MaxHeap(int capacity){data = (T[])new Object[capacity+1];count = 0;}// 返回堆中的元素个数public int size(){return count;}// 返回一个布尔值, 表示堆中是否为空public boolean isEmpty(){return count == 0;}// 测试 MaxHeappublic static void main(String[] args) {MaxHeap<Integer> maxHeap = new MaxHeap<Integer>(100);System.out.println(maxHeap.size());}
}相关文章:

堆的基本存储
一、概念及其介绍堆(Heap)是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵完全二叉树的数组对象。堆满足下列性质:堆中某个节点的值总是不大于或不小于其父节点的值。堆总是一棵完全二叉树。二、适用说明堆是利用完全二叉树的结构来维护一组数…...

如何获取物体立体信息通过一个相机
大家都知道的3D 技术是通过双眼视觉差异 得到的 但是3D的深度并没有那么强 为什么眼睛看到的就那么强 这无法让我们相信这个视觉差理论是和人眼睛立体感是一个原理 这个如今3D 电影都在用的技术 是和真正的人眼立体感 不一样的 或者说是有瑕疵的 分析一下现在的立体感技术 是通…...
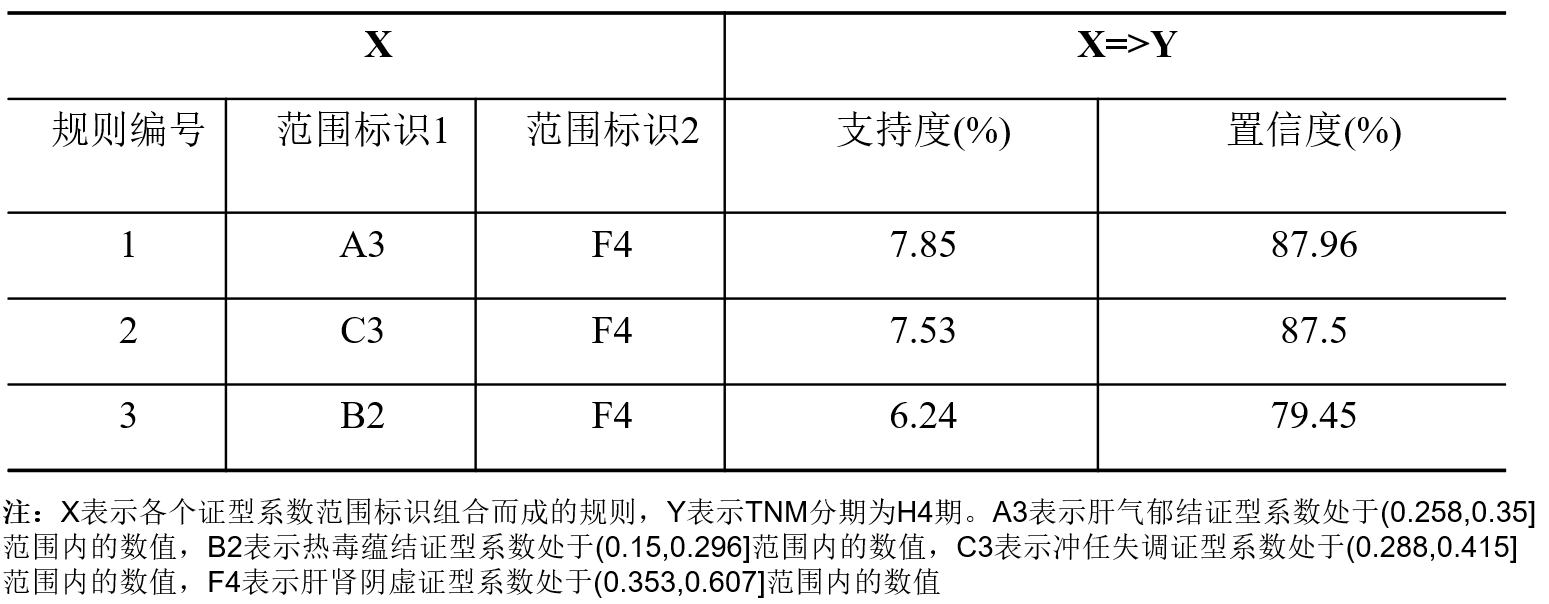
【数据挖掘实战】——中医证型的关联规则挖掘(Apriori算法)
目录 一、背景和挖掘目标 1、问题背景 2、传统方法的缺陷 3、原始数据情况 4、挖掘目标 二、分析方法和过程 1、初步分析 2、总体过程 第1步:数据获取 第2步:数据预处理 第3步:构建模型 三、思考和总结 项目地址:Data…...
一些硬件学习的注意事项与快捷方法
xilinx系列软件 系统适用版本 要安装在Ubuntu系统的话,要注意提前看好软件适用的版本,不要随便安好了Ubuntu系统又发现对应版本的xilinx软件不支持。 如下图,发行说明中会说明这个版本的软件所适配的系统版本。 下载 vivado vitis这些都可以…...
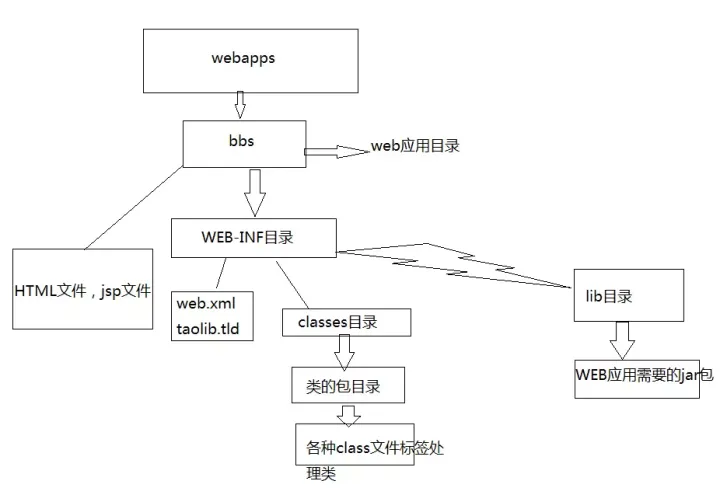
【Tomcat】Tomcat安装及环境配置
文章目录什么是Tomcat为什么我们需要用到Tomcattomcat下载及安装1、进入官网www.apache.org,找到Projects中的project List2、下载之后,解压3、找到tomcat目录下的startup.bat文件,双击之后最后结果出现多少多少秒,表示安装成功4、…...
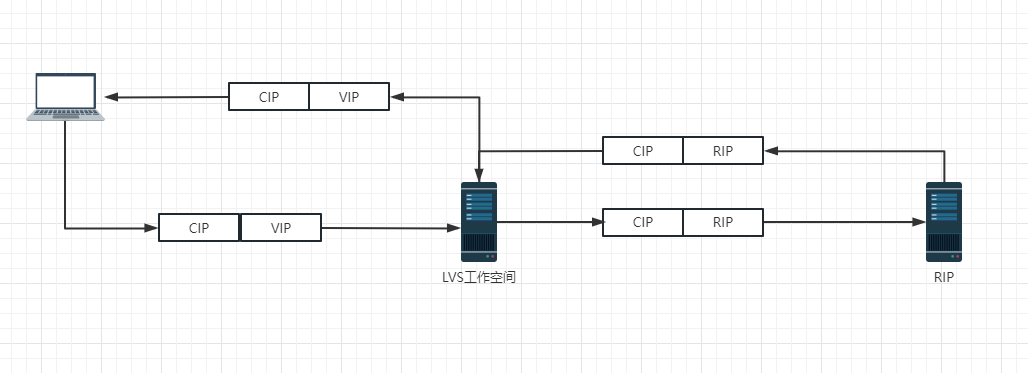
负载均衡:LVS 笔记(二)
文章目录LVS 二层负载均衡机制LVS 三层负载均衡机制LVS 四层负载均衡机制LVS 调度算法轮叫调度(RR)加权轮叫调度(WRR)最小连接调度(LC)加权最小连接调度(WLC)基于局部性的最少链接调…...
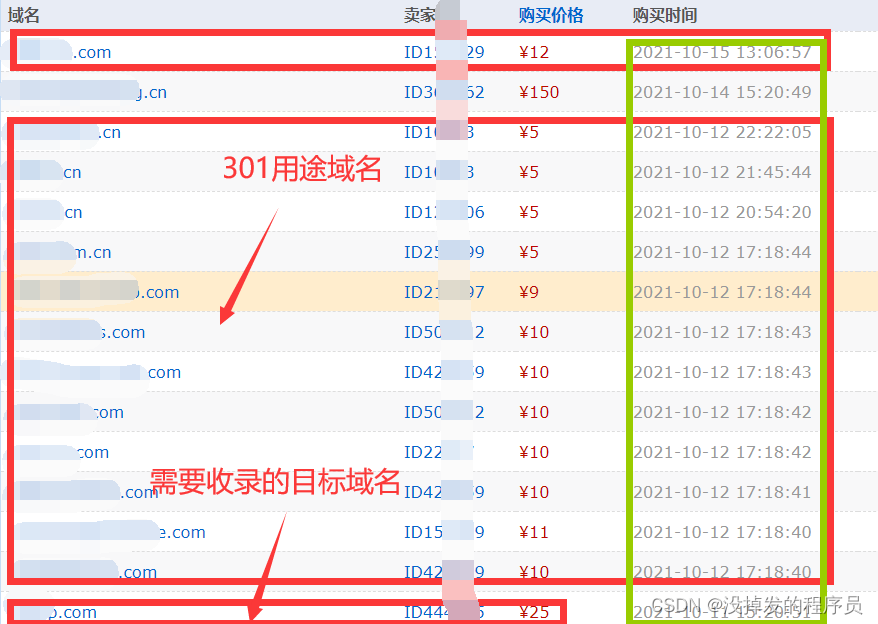
SEO优化:干货技巧分享,包新站1-15天100%收录首页
不管是老域名还是新域名,不管是多久没有收录首页的站,此法周期7-30天,包首页收录!本人不喜欢空吹牛逼不实践的理论,公布具体操作:假如你想收录的域名是a.com,那么准备如下材料1.购买5-10个最便宜…...

JavaWeb测试题
【第四小组】【姓名:郑梦飞】说明:上方【组】填入所在的组,上方【姓名】填入自己的真实姓名。答题方式,基于Word文档基础上答题编程题可利用工具编程完以后,复制到该文档内。答完以后,导成PDF。以姓名.PDF命…...
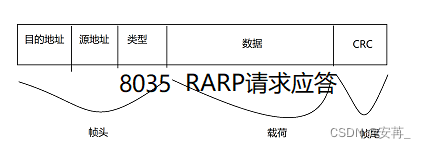
Java EE|TCP/IP协议栈之数据链路层协议详解
文章目录一、数据链路层协议感性认识数据链路层简介以太网简介特点二、以太网数据帧格式详解帧头不同类型对应的载荷三、关于MTU什么是MTUMTU有什么作用ip分片(了解)参考一、数据链路层协议感性认识 数据链路层简介 从上图可以看出 , 在TCP/…...
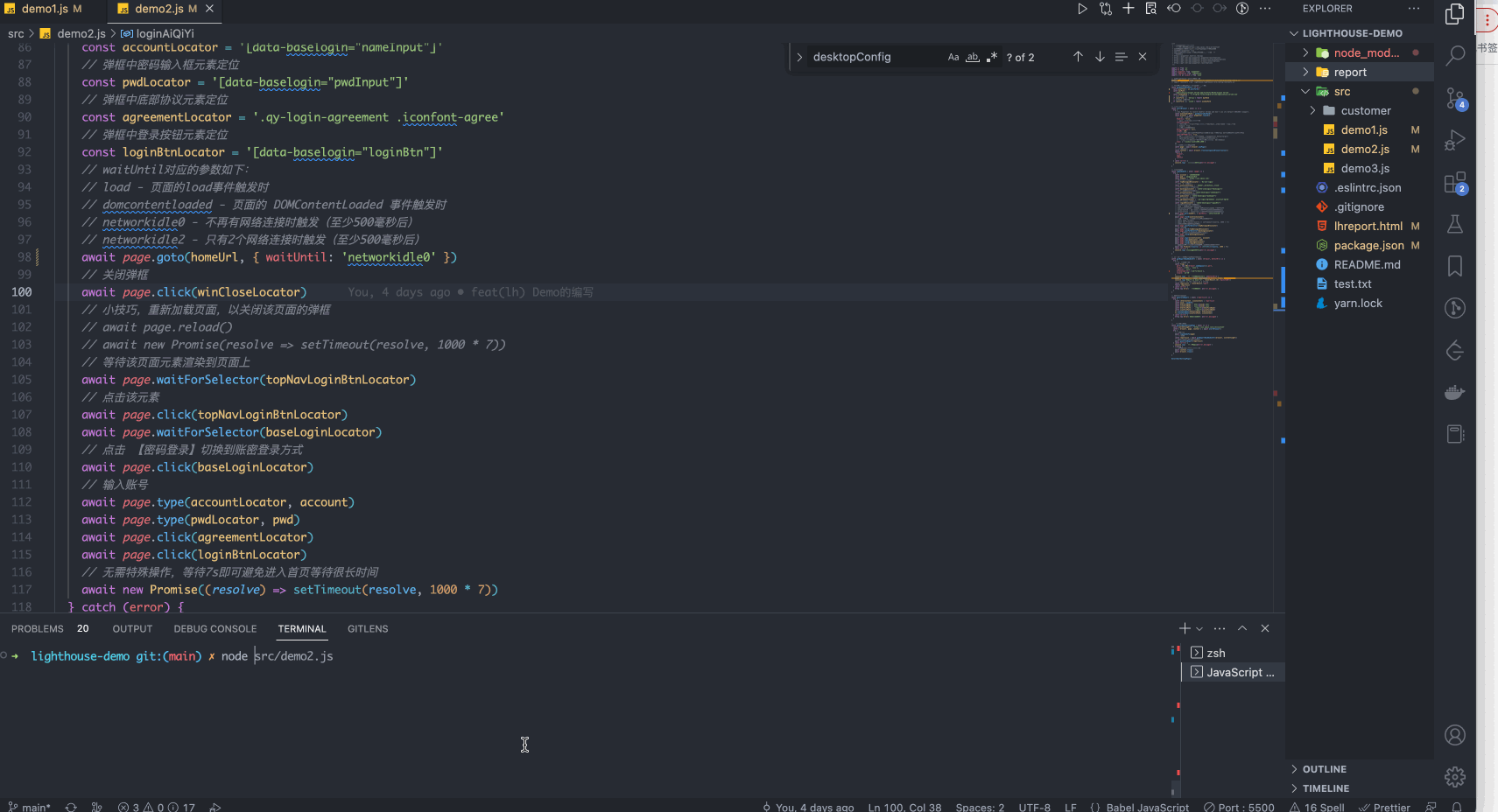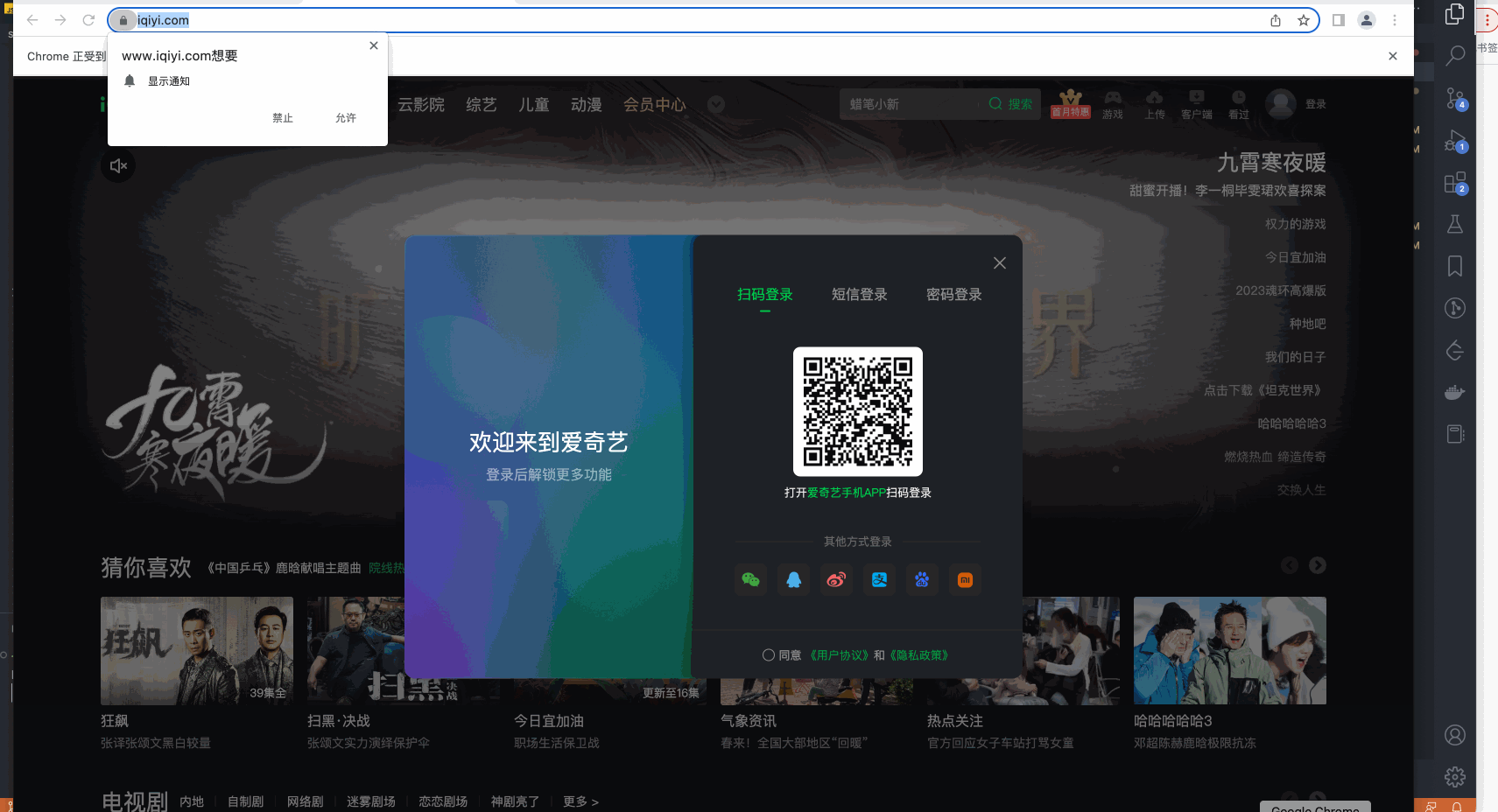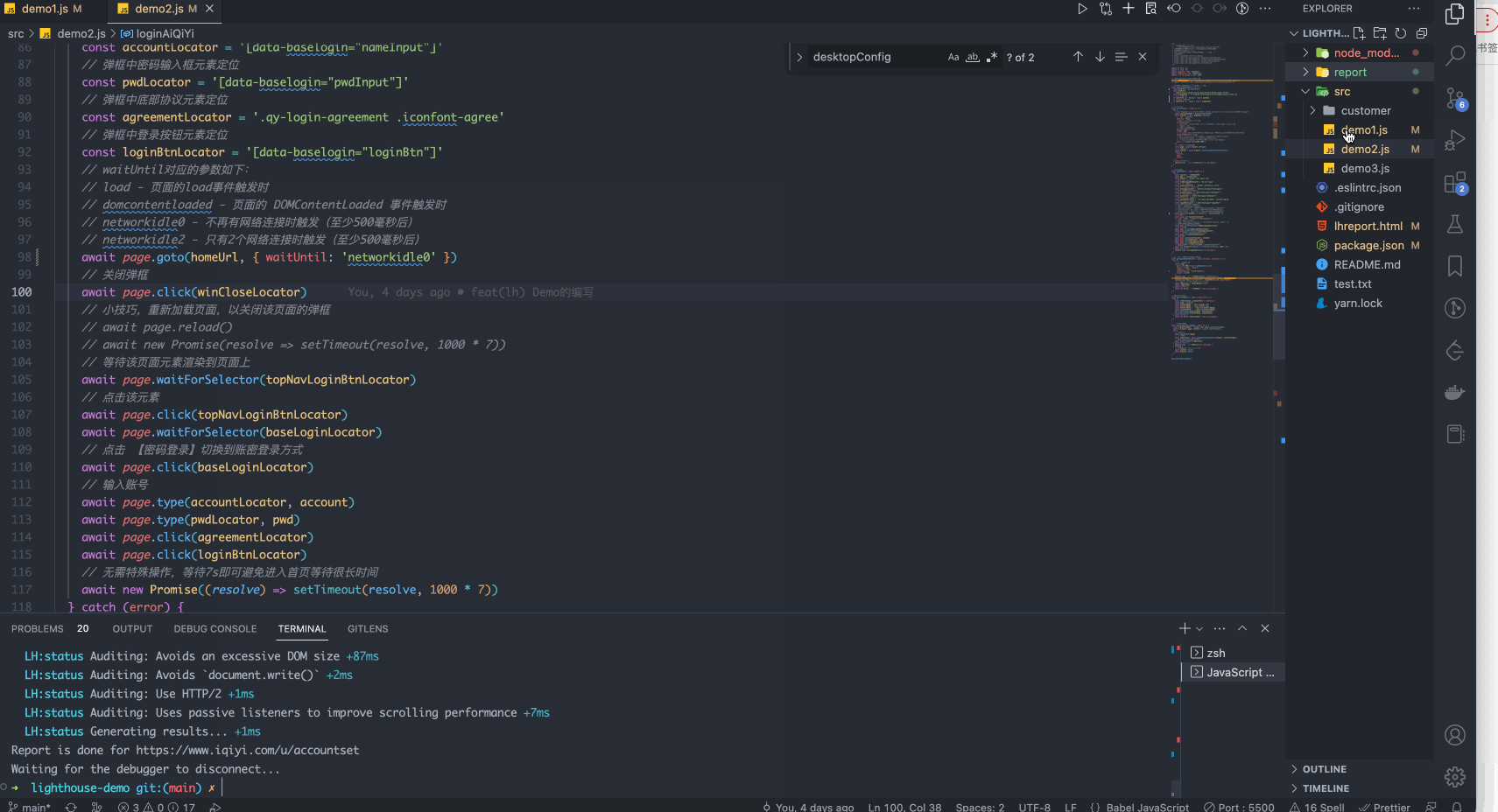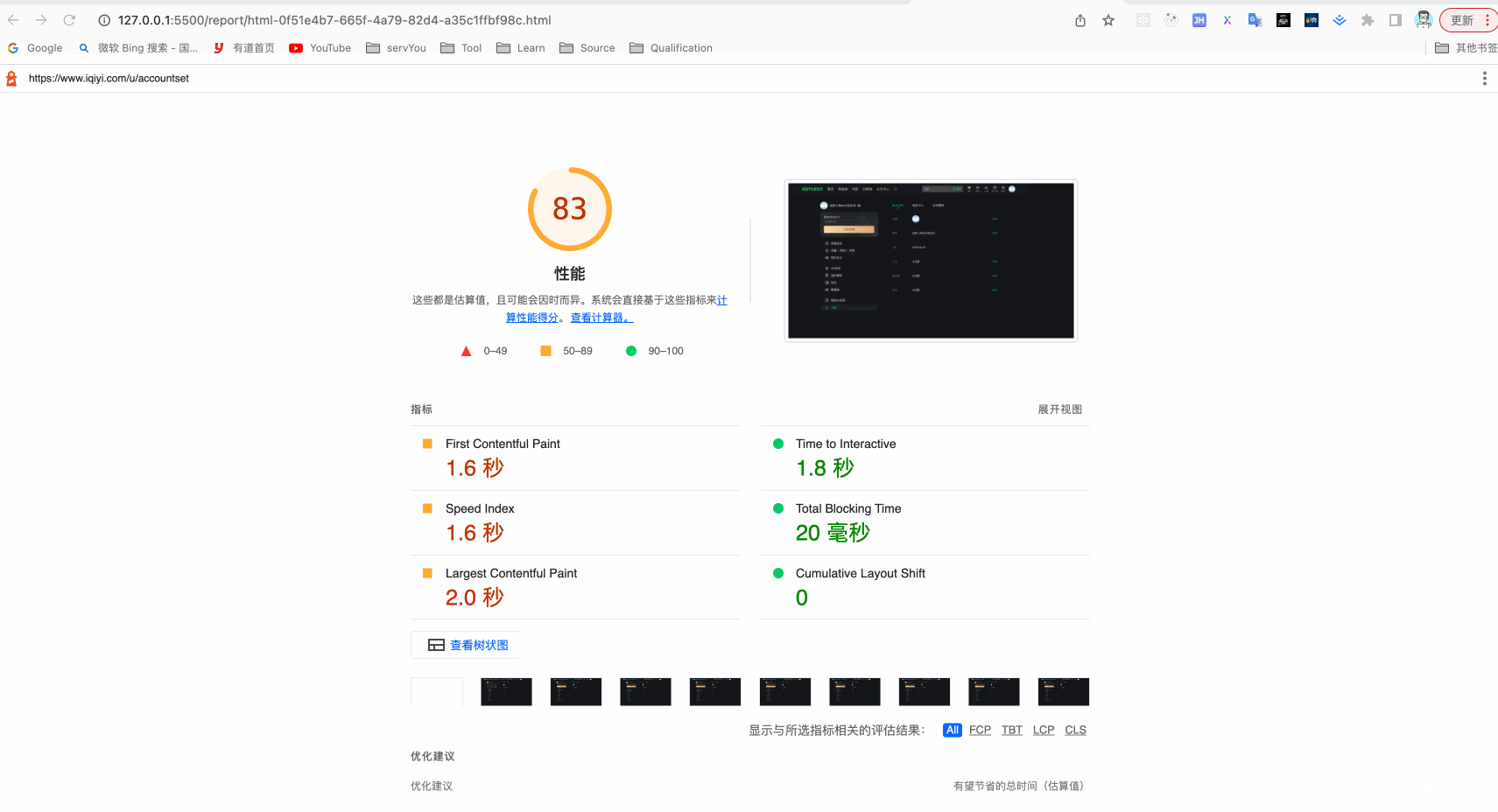
Lighthouse组合Puppeteer检测页面
如上一篇文章lighthouse的介绍和基本使用方法结尾提到的一样,我们在实际使用Lighthouse检测页面性能时,通常需要一定的业务前置条件,比如最常见的登录操作、如果没有登录态就没有办法访问其他页面。再比如有一些页面是需要进行一系列的操作&a…...
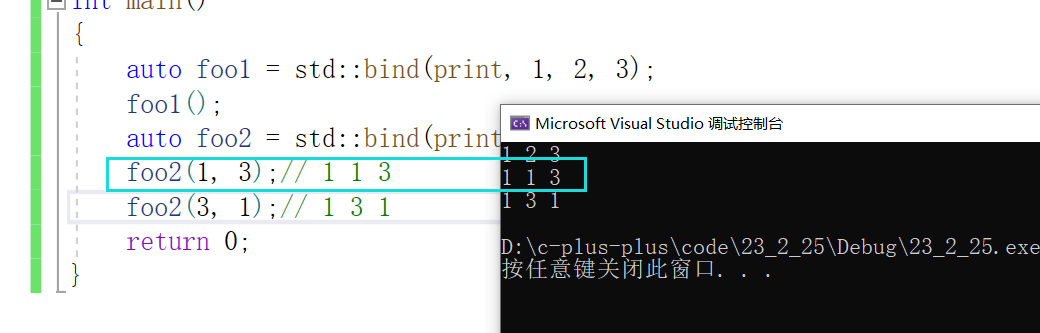
【C++】仿函数、lambda表达式、包装器
1.仿函数 仿函数是什么?仿函数就是类中的成员函数,这个成员函数可以让对象模仿函数调用的行为。 函数调用的行为:函数名(函数参数)C中可以让类实现:函数名(函数参数)调用函数 自己写一个仿函数: 重载()运算符 cla…...
)
二叉树(二)
二叉树——堆存储1.堆的初始化2. 堆的销毁3.堆的插入4.堆的删除5.堆的打印6.取堆顶的数据7.堆的数据个数8.堆的判空9.堆的构建10.向上调整11.向下调整12.使用堆进行排序13.交换14.完整代码🌟🌟hello,各位读者大大们你们好呀🌟&…...

爬虫知识简介
爬虫简介 爬虫与网络请求 网络爬虫是一个自动提取网页的程序,一般都分为3步:数据爬取,数据解析,数据存储。数据爬取就是模拟浏览器发送请求,所以需要对网络请求HTTP/HTTPS有一定了解 相关概念: H…...

2023年全国最新会计专业技术资格精选真题及答案6
百分百题库提供会计专业技术资格考试试题、会计考试预测题、会计专业技术资格考试真题、会计证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 11.下列各项中,企业根据本月“工资费用分配汇总表”分配所列财务部门…...

同时学习C++语言和C#语言好吗?
同时学习两门编程语言并不是不好的选择,尤其是对于初学者而言,这样做能够帮助你更好地理解编程语言的基本概念和原则。C和C#都是常用的编程语言,它们都有各自的优点和用途。同时学习这两门语言能够让你更好地理解它们之间的异同点,…...

Android8,source与lunch流程解析
source 流程 # build/make/envsetup.sh ---- # Execute the contents of any vendorsetup.sh files we can find. for f in test -d device && find -L device -maxdepth 4 -name vendorsetup.sh 2> /dev/null | sort \ test -d vendor && find -L vendo…...
大数据NiFi(二十):实时同步MySQL数据到Hive
文章目录 实时同步MySQL数据到Hive 一、开启MySQL的binlog日志 1、登录mysql查看MySQL是否开启binlog日志 2 、开启mysql binlog日志 3、重启mysql 服务,重新查看binlog日志情况 二、配置“CaptureChangeMySQL”处理器 1、创建“…...
mac 如何设置 oh my zsh 终端terminal 和添加主题powerlevel10k
Oh My Zsh 是什么 Oh My Zsh 是一款社区驱动的命令行工具,正如它的主页上说的,Oh My Zsh 是一种生活方式。它基于 zsh 命令行,提供了主题配置,插件机制,已经内置的便捷操作。给我们一种全新的方式使用命令行。 **Oh …...
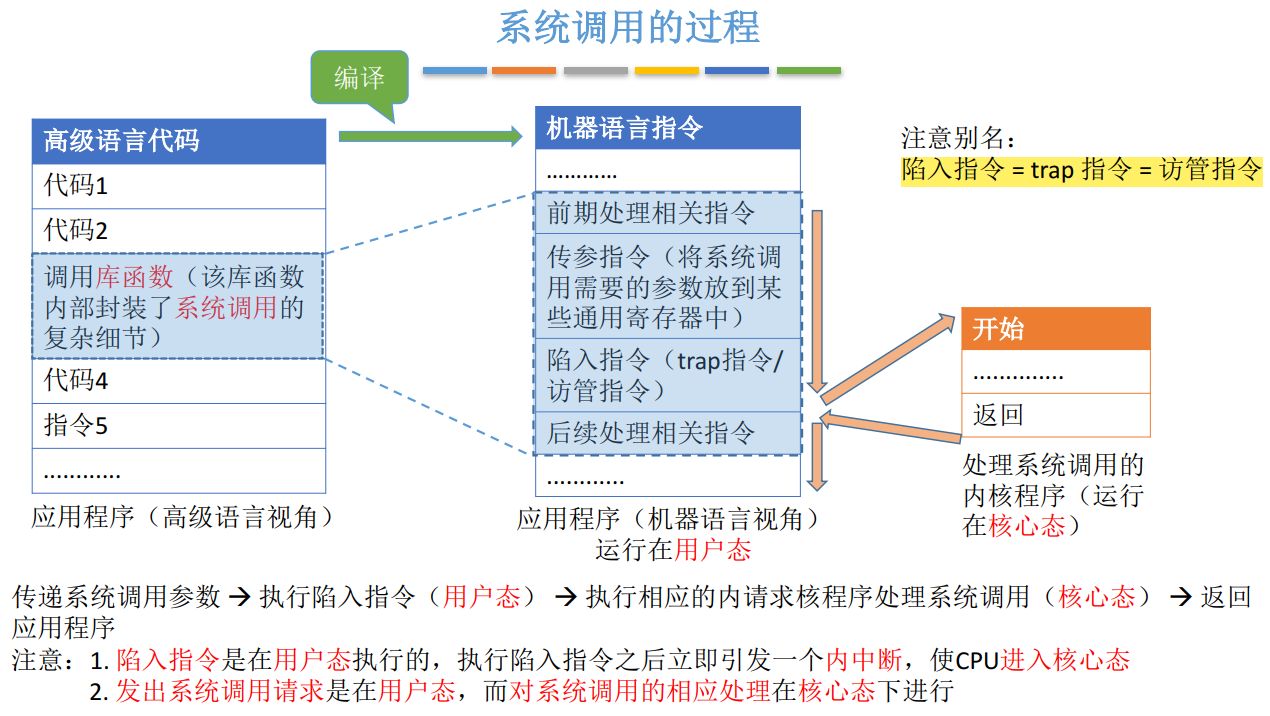
王道《操作系统》学习(一)——计算机系统概述
1.1 操作系统的概念、功能 1.1.1 操作系统的概念(定义) (1)操作系统是系统资源的管理者 (2)向上层用户、软件提供方便易用的服务 (3)是最接近硬件的一层软件 1.1.2 操作系统的功能…...

什么是自适应平台服务?
总目录链接==>> AutoSAR入门和实战系列总目录 文章目录 什么是自适应平台服务?1.1 自适应平台服务包含哪些功能簇呢?1.1.1 ara::sm 状态管理 (SM)1.1.2 ara::diag 诊断管理 (DM)1.1.3 ara::s2s 信号到服务映射1.1.4 ara::nm 网络管理 (NM)1.1.5 ara::ucm 更新和配置管…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...
