分类预测 | Matlab实现KOA-CNN-BiLSTM-selfAttention多特征分类预测(自注意力机制)
分类预测 | Matlab实现KOA-CNN-BiLSTM-selfAttention多特征分类预测(自注意力机制)
目录
- 分类预测 | Matlab实现KOA-CNN-BiLSTM-selfAttention多特征分类预测(自注意力机制)
- 分类效果
- 基本描述
- 程序设计
- 参考资料
分类效果






基本描述
1.Matlab实现KOA-CNN-BiLSTM-selfAttention开普勒算法优化卷积双向长短期记忆神经网络融合自注意力多特征分类预测,多特征输入模型,运行环境Matlab2023b及以上;
2.基于开普勒算法(KOA)优化卷积双向长短期记忆神经网络(CNN-BiLSTM)结合自注意力机制(selfAttention)分类预测。2023年新算法KOA,MATLAB程序,多行变量特征输入,优化了学习率、卷积核大小及隐藏层单元数等。
3.多特征输入单输出的二分类及多分类模型。程序内注释详细,直接替换数据就可以用。程序语言为matlab,程序可出分类效果图,迭代图,混淆矩阵图.
4.data为数据集,输入12个特征,分四类;main为主程序,其余为函数文件,无需运行。
5.输出指标包括优化参数、精确度、召回率、精确率、F1分数。
程序设计
- 完整程序和数据获取方式,私信博主回复Matlab实现KOA-CNN-BiLSTM-selfAttention多特征分类预测(自注意力机制)。
[Order] = sort(PL_Fit); %% 对当前种群中的解的适应度值进行排序%% 函数评估t时的最差适应度值worstFitness = Order(SearchAgents_no); %% Eq.(11)M = M0 * (exp(-lambda * (t / Tmax))); %% Eq.(12)%% 计算表示太阳与第i个解之间的欧几里得距离Rfor i = 1:SearchAgents_noR(i) = 0;for j = 1:dimR(i) = R(i) + (Sun_Pos(j) - Positions(i, j))^2; %% Eq.(7)endR(i) = sqrt(R(i));end%% 太阳和对象i在时间t的质量计算如下:for i = 1:SearchAgents_nosum = 0;for k = 1:SearchAgents_nosum = sum + (PL_Fit(k) - worstFitness);endMS(i) = rand * (Sun_Score - worstFitness) / (sum); %% Eq.(8)m(i) = (PL_Fit(i) - worstFitness) / (sum); %% Eq.(9)end%% 第2步:定义引力(F)% 计算太阳和第i个行星的引力,根据普遍的引力定律:for i = 1:SearchAgents_noRnorm(i) = (R(i) - min(R)) / (max(R) - min(R)); %% 归一化的R(Eq.(24))MSnorm(i) = (MS(i) - min(MS)) / (max(MS) - min(MS)); %% 归一化的MSMnorm(i) = (m(i) - min(m)) / (max(m) - min(m)); %% 归一化的mFg(i) = orbital(i) * M * ((MSnorm(i) * Mnorm(i)) / (Rnorm(i) * Rnorm(i) + eps)) + (rand); %% Eq.(6)end
% a1表示第i个解在时间t的椭圆轨道的半长轴,
for i = 1:SearchAgents_noa1(i) = rand * (T(i)^2 * (M * (MS(i) + m(i)) / (4 * pi * pi)))^(1/3); %% Eq.(23)
endfor i = 1:SearchAgents_no
% a2是逐渐从-1到-2的循环控制参数
a2 = -1 - 1 * (rem(t, Tmax / Tc) / (Tmax / Tc)); %% Eq.(29)% ξ是从1到-2的线性减少因子
n = (a2 - 1) * rand + 1; %% Eq.(28)
a = randi(SearchAgents_no); %% 随机选择的解的索引
b = randi(SearchAgents_no); %% 随机选择的解的索引
rd = rand(1, dim); %% 按照正态分布生成的向量
r = rand; %% r1是[0,1]范围内的随机数%% 随机分配的二进制向量
U1 = rd < r; %% Eq.(21)
O_P = Positions(i, :); %% 存储第i个解的当前位置%% 第6步:更新与太阳的距离(第3、4、5在后面)
if rand < rand% h是一个自适应因子,用于控制时间t时太阳与当前行星之间的距离h = (1 / (exp(n * randn))); %% Eq.(27)% 基于三个解的平均向量:当前解、迄今为止的最优解和随机选择的解Xm = (Positions(b, :) + Sun_Pos + Positions(i, :)) / 3.0;Positions(i, :) = Positions(i, :) .* U1 + (Xm + h .* (Xm - Positions(a, :))) .* (1 - U1); %% Eq.(26)
else参考资料
[1] https://blog.csdn.net/kjm13182345320/article/details/129036772?spm=1001.2014.3001.5502
[2] https://blog.csdn.net/kjm13182345320/article/details/128690229
相关文章:

分类预测 | Matlab实现KOA-CNN-BiLSTM-selfAttention多特征分类预测(自注意力机制)
分类预测 | Matlab实现KOA-CNN-BiLSTM-selfAttention多特征分类预测(自注意力机制) 目录 分类预测 | Matlab实现KOA-CNN-BiLSTM-selfAttention多特征分类预测(自注意力机制)分类效果基本描述程序设计参考资料 分类效果 基本描述 1…...

浮点数和定点数(上):怎么用有限的Bit表示尽可能多的信息?
目录 背景 浮点数的不精确性 定点数的表示 浮点数的表示 小结 背景 在我们日常的程序开发中,不只会用到整数。更多情况下,我们用到的都是实数。比如,我们开发一个电商 App,商品的价格常常会是 9 块 9;再比如&…...
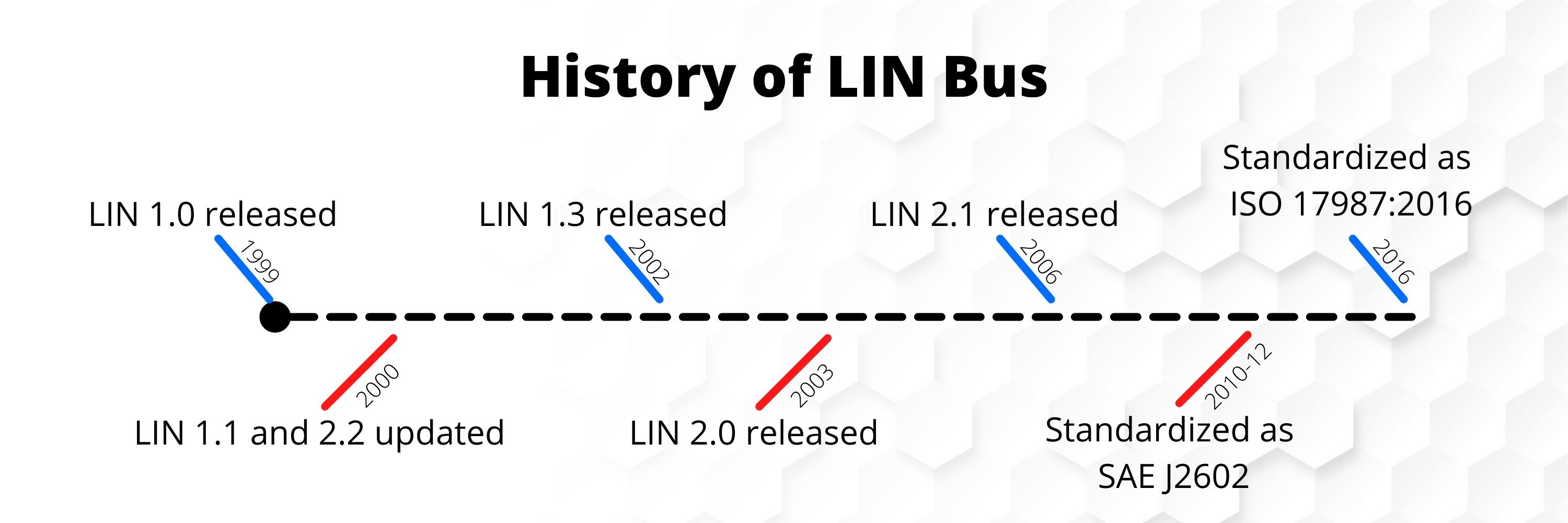
一文详解汽车电子LIN总线
0.摘要 汽车电子LIN总线不同于CAN总线。 LIN总线基本上是CAN总线的廉价补充,相比于CAN总线,它提供较低的可靠性和性能。同时LIN总线也是一个应用非常广泛的网络协议,并且越来越受欢迎。 再一次,我们准备了一个关于LIN总线的简要…...
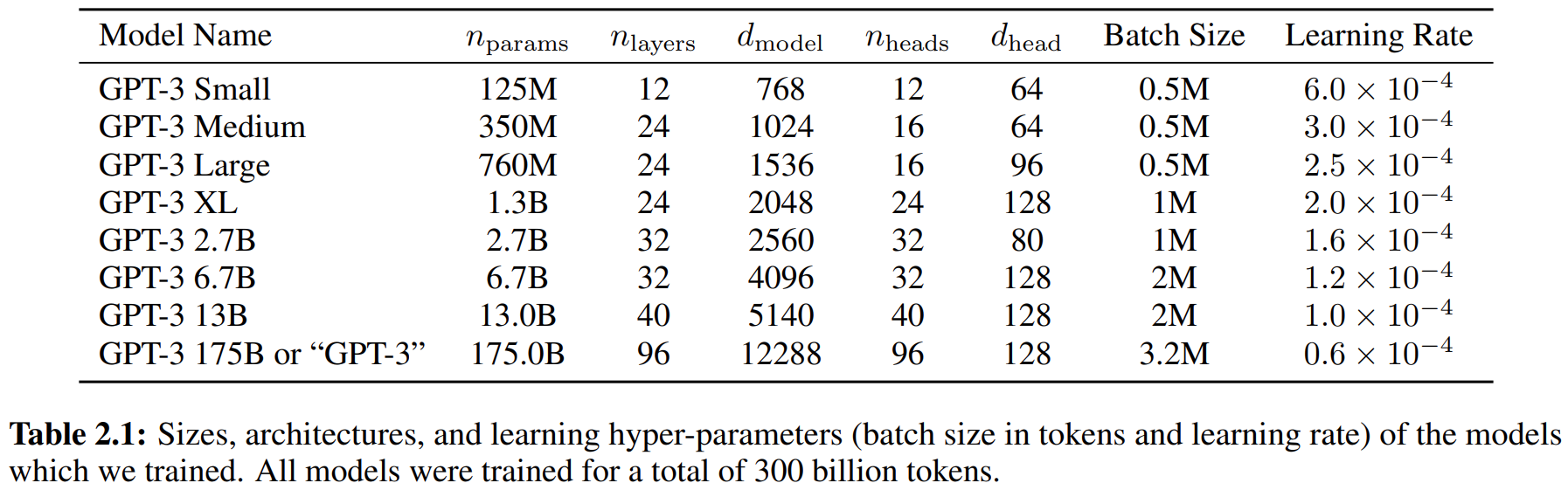
论文阅读——GPT3
来自论文:Language Models are Few-Shot Learners Arxiv:https://arxiv.org/abs/2005.14165v2 记录下一些概念等。,没有太多细节。 预训练LM尽管任务无关,但是要达到好的效果仍然需要在特定数据集或任务上微调。因此需要消除这个…...
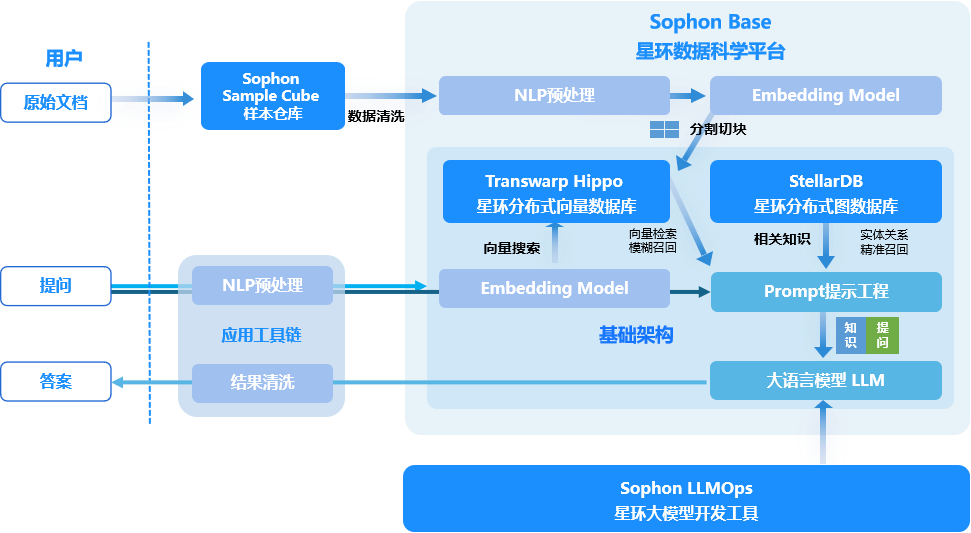
星环科技分布式向量数据库Transwarp Hippo正式发布,拓展大语言模型时间和空间维度
随着企业、机构中非结构化数据应用的日益增多以及AI的爆发式增长所带来的大量生成式数据,所涉及的数据呈现了体量大、格式和存储方式多样、处理速度要求高、潜在价值大等特点。但传统数据平台对这些数据的处理能力较为有限,如使用文件系统、多类不同数据…...
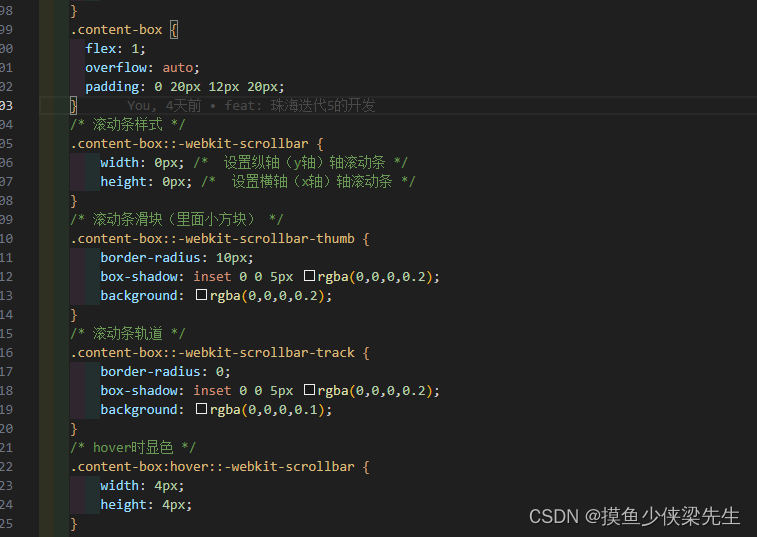
滚动条默认是隐藏的只有鼠标移上去才会显示
效果 在设置滚动条的类名中写 /* 滚动条样式 */.content-box::-webkit-scrollbar {width: 0px; /* 设置纵轴(y轴)轴滚动条 */height: 0px; /* 设置横轴(x轴)轴滚动条 */}/* 滚动条滑块(里面小方块) */.…...
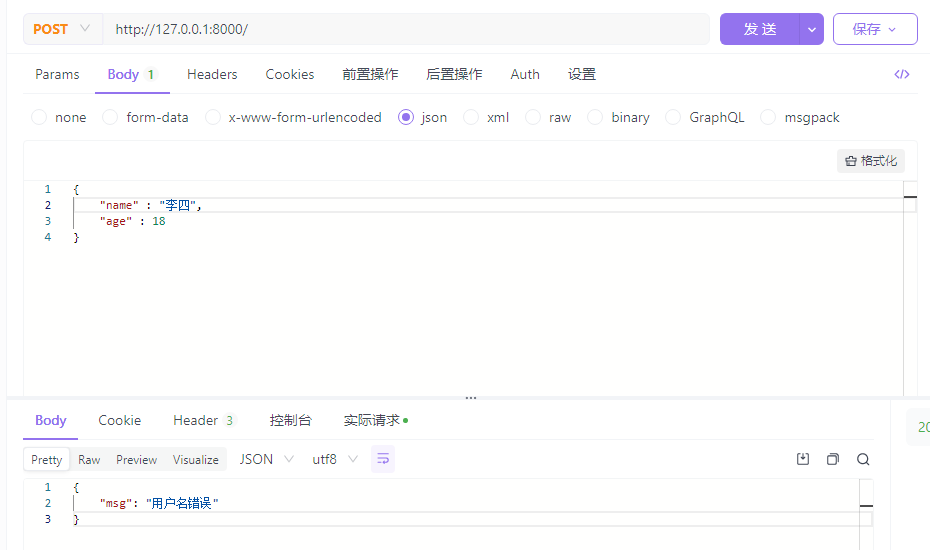
Go学习第十五章——Gin参数绑定bind与验证器
Go web框架——Gin(参数绑定bind与验证器) 1 bind参数绑定1.1 JSON参数1.2 Query参数1.3 Uri绑定动态参数1.4 ShouldBind自动绑定 2 验证器2.1 常用验证器2.2 gin内置验证器2.3 自定义验证的错误信息2.4 自定义验证器 1 bind参数绑定 在Gin框架中&#…...

EtherCAT的4种寻址方式解析
我们知道,一个EtherCAT数据帧(frame)里面包含很多个报文(datagram),不管是什么样式的报文,它们的目的只有一个,就是读写从站寄存器或内存。所以寻址就是以什么方式访问哪个从站的哪个…...
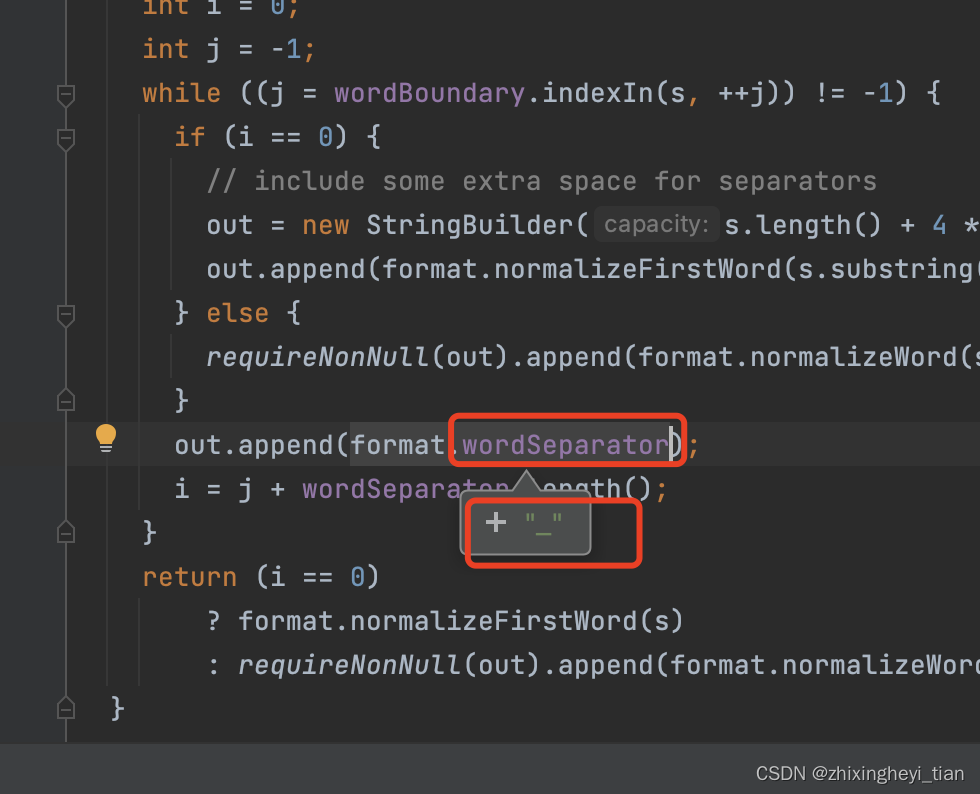
Trino 源码剖析
Functions function 反射和注册 io.trino.operator.scalar.annotations.ScalarFromAnnotationsParser 这里是提取注解元素的方法 String baseName scalarFunction.value().isEmpty() ? camelToSnake(annotatedName(annotated)) : scalarFunction.value(); 这里如果 scala…...

element表格自定义筛选
文章目录 前言一、简介二、效果展示三、源码总结 前言 提示:这里可以添加本文要记录的大概内容: …待续 提示:以下是本篇文章正文内容,下面案例可供参考 一、简介 修改el-table的筛选…待续 二、效果展示 三、源码 使用方法…...

全方位 Linux 性能调优经验总结
Part1Linux性能优化 1性能优化 性能指标 高并发和响应快对应着性能优化的两个核心指标:吞吐和延时 图片来自: www.ctq6.cn 应用负载角度:直接影响了产品终端的用户体验系统资源角度:资源使用率、饱和度等 性能问题的本质就是系统资源已经…...

Linux机器网络检查
查看DNS file: dianTestLRSSnapshot:~$ cat /etc/resolv.conf # This file is managed by man:systemd-resolved(8). Do not edit. # # This is a dynamic resolv.conf file for connecting local clients to the # internal DNS stub resolver of systemd-resolved. This file…...

使用示例和应用程序全面了解高效数据管理的Golang MySQL数据库
Golang,也被称为Go,已经成为构建强大高性能应用程序的首选语言。在处理MySQL数据库时,Golang提供了一系列强大的库,简化了数据库交互并提高了效率。在本文中,我们将深入探讨一些最流行的Golang MySQL数据库库ÿ…...

ubuntu 22.04 源码安装 apollo 8.0
对于其他的关于GPU的安装包需求,这里不再列出,因为我之前安装过,偷个懒就不写了,哈哈哈哈1, 安装docker 安装docker命令(这里的安装命令都是在docker官网,还有安装包): 1, 设置docker的apt仓库 # Add Do…...

RK3588编译MXNet框架
目录 1. 背景 2.编译MXNet准备 3.开发板编译 1. 背景 MXNet(也称为Apache MXNet或incubator-mxnet)是一个开源的深度学习框架,它最初由华为和亚马逊AWS共同开发,并于2017年成为Apache软件基金会的孵化项目。MXNet旨在提供高效、…...

港府Web3宣言周年思考:合规困境中的“隐患”
出品|欧科云链研究院 作者|毕良寰 距离《有关虚拟资产在港发展的政策宣言》已过去一年,我们欧科云链研究院在分析全球几个主要国家和地区对Web3的监管政策及态度后,对港府的雄心壮志充满期待。然而,由于近期一些庞氏骗…...

vue点击按钮跳转页面
在Vue.js中,你可以使用<router-link>或this.$router.push()来实现点击按钮跳转页面的功能,前提是你已经配置了Vue Router。以下是两种不同的方法来实现页面跳转: 方法一:使用<router-link> <router-link> 是Vu…...

大中小企业对CRM系统的需求
在以前,CRM客户管理系统是大型企业的专属。如今,不论何种规模的企业都能够使用CRM系统。市面上的CRM有着丰富的功能类型,管理者可以从企业自身规模出发,选择适合的CRM系统。下面说说,大中小企业对CRM系统的需求。 一句…...

.net core iis 发布后登入的时候请求不到方法报错502
.net core iis 发布后登入的时候请求不到方法报错502 502 bad gateway 502 - Web 服务器在作为网关或代理服务器时收到了无效响应。 您要查找的页面有问题,无法显示。当 Web 服务器(作为网关或代理)与上游内容服务器联系时,收到来自内容服务器的无效…...
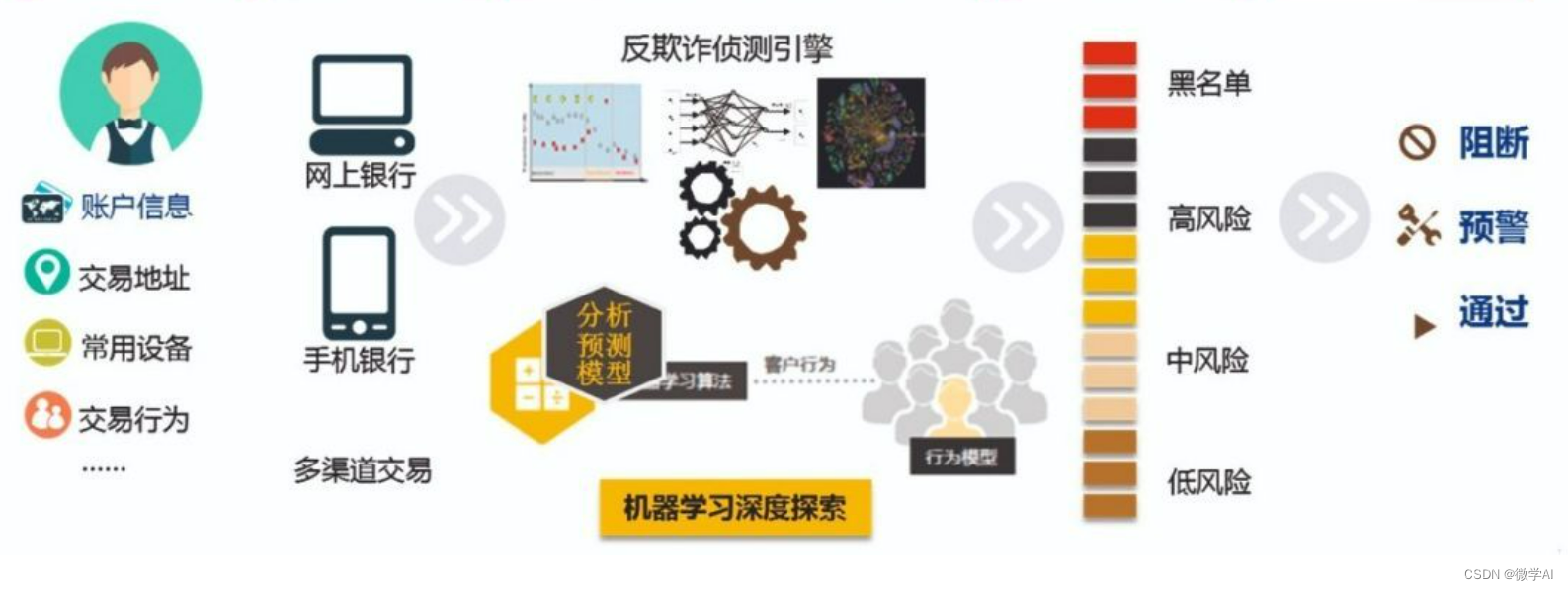
知识图谱实战应用30-知识图谱在反欺诈情报分析项目中的应用实践
大家好,我是微学AI,今天给大家介绍一下知识图谱实战应用30-知识图谱在反欺诈情报分析项目中的应用实践,现代商业环境中,各类欺诈行为日益猖獗,严重影响企业的运营和社会秩序。传统的欺诈检测方法难以满足实时性和有效性方面的要求。本文介绍了采用知识图谱技术构建反欺诈情报…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

人工智能--安全大模型训练计划:基于Fine-tuning + LLM Agent
安全大模型训练计划:基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标:为安全大模型创建高质量、去偏、符合伦理的训练数据集,涵盖安全相关任务(如有害内容检测、隐私保护、道德推理等)。 1.1 数据收集 描…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...

es6+和css3新增的特性有哪些
一:ECMAScript 新特性(ES6) ES6 (2015) - 革命性更新 1,记住的方法,从一个方法里面用到了哪些技术 1,let /const块级作用域声明2,**默认参数**:函数参数可以设置默认值。3&#x…...

Java并发编程实战 Day 11:并发设计模式
【Java并发编程实战 Day 11】并发设计模式 开篇 这是"Java并发编程实战"系列的第11天,今天我们聚焦于并发设计模式。并发设计模式是解决多线程环境下常见问题的经典解决方案,它们不仅提供了优雅的设计思路,还能显著提升系统的性能…...
