回归预测 | Matlab实现RIME-CNN-SVM霜冰优化算法优化卷积神经网络-支持向量机的多变量回归预测
回归预测 | Matlab实现RIME-CNN-SVM霜冰优化算法优化卷积神经网络-支持向量机的多变量回归预测
目录
- 回归预测 | Matlab实现RIME-CNN-SVM霜冰优化算法优化卷积神经网络-支持向量机的多变量回归预测
- 效果一览
- 基本介绍
- 程序设计
- 参考资料
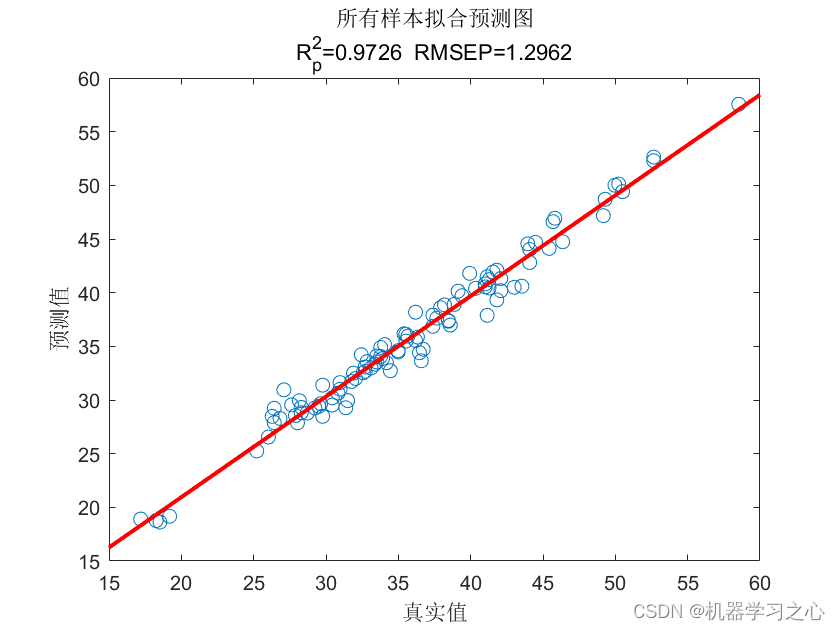
效果一览







基本介绍
1.RIME-CNN-SVM霜冰优化算法优化卷积神经网络-支持向量机的多变量回归预测 可直接运行Matlab;
2.评价指标包括: R2、MAE、RMSE和MAPE等,代码质量极高,方便学习和替换数据。要求2021版本及以上。
3.2023年新算法霜冰优化算法RIME优化的参数为:CNN的批处理大小、学习率、正则化系数,能够避免人工选取参数的盲目性,有效提高其预测精度。
4.main.m为主程序,其他为函数文件,无需运行,data为数据,多输入单输出,数据回归预测,输入7个特征,输出1个变量,直接替换Excel数据即可用!注释清晰,适合新手小白~
程序设计
- 完整程序和数据获取方式:私信博主回复Matlab实现RIME-CNN-SVM霜冰优化算法优化卷积神经网络-支持向量机的多变量回归预测;
while it <= Max_iteritRimeFactor = (rand-0.5)*2*cos((pi*it/(Max_iter/10)))*(1-round(it*W/Max_iter)/W);%Parameters of Eq.(3),(4),(5)E =(it/Max_iter)^0.5;%Eq.(6)newRimepop = Rimepop;%Recording new populationsnormalized_rime_rates=normr(Rime_rates);%Parameters of Eq.(7)for i=1:Nfor j=1:dim%Soft-rime search strategyr1=rand();if r1< EnewRimepop(i,j)=Best_rime(1,j)+RimeFactor*((Ub(j)-Lb(j))*rand+Lb(j));%Eq.(3)end%Hard-rime puncture mechanismr2=rand();if r2<normalized_rime_rates(i)newRimepop(i,j)=Best_rime(1,j);%Eq.(7)endendendfor i=1:N%Boundary absorptionFlag4ub=newRimepop(i,:)>ub;Flag4lb=newRimepop(i,:)<lb;newRimepop(i,:)=(newRimepop(i,:).*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;newRime_rates(1,i)=fobj(newRimepop(i,:));%Positive greedy selection mechanismif newRime_rates(1,i)<Rime_rates(1,i)Rime_rates(1,i) = newRime_rates(1,i);Rimepop(i,:) = newRimepop(i,:);if newRime_rates(1,i)< Best_rime_rateBest_rime_rate=Rime_rates(1,i);Best_rime=Rimepop(i,:);endendend参考资料
[1] https://blog.csdn.net/kjm13182345320/article/details/129036772?spm=1001.2014.3001.5502
[2] https://blog.csdn.net/kjm13182345320/article/details/128690229
相关文章:

回归预测 | Matlab实现RIME-CNN-SVM霜冰优化算法优化卷积神经网络-支持向量机的多变量回归预测
回归预测 | Matlab实现RIME-CNN-SVM霜冰优化算法优化卷积神经网络-支持向量机的多变量回归预测 目录 回归预测 | Matlab实现RIME-CNN-SVM霜冰优化算法优化卷积神经网络-支持向量机的多变量回归预测效果一览基本介绍程序设计参考资料 效果一览 基本介绍 1.RIME-CNN-SVM霜冰优化算…...

使用Jaeger进行分布式跟踪:学习如何在服务网格中使用Jaeger来监控和分析请求的跟踪信息
🌷🍁 博主猫头虎 带您 Go to New World.✨🍁 🦄 博客首页——猫头虎的博客🎐 🐳《面试题大全专栏》 文章图文并茂🦕生动形象🦖简单易学!欢迎大家来踩踩~🌺 &a…...

添加多个单元对象
开发环境: Windows 11 家庭中文版Microsoft Visual Studio Community 2019VTK-9.3.0.rc0vtk-example参考代码 demo解决问题:不同阶段添加多个单元对象。 定义一个点集和一个单元集合,单元的类型可以是点、三角形、矩形、多边形等基本图形。只…...
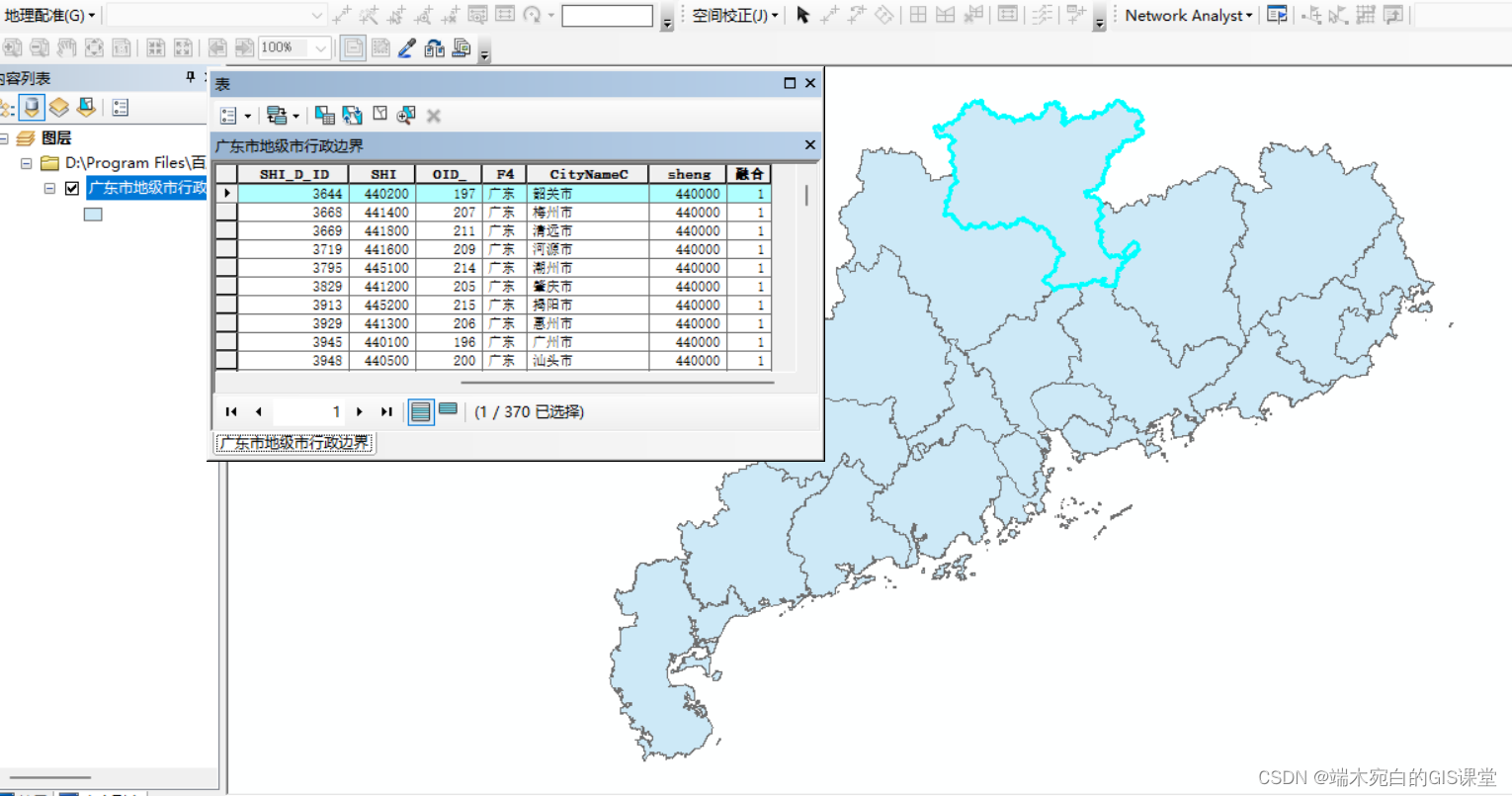
十八、模型构建器(ModelBuilder)快速提取城市建成区——批量掩膜提取夜光数据、夜光数据转面、面数据融合、要素转Excel(基于参考比较法)
一、前言 前文实现批量投影栅格、转为整型,接下来重点实现批量提取夜光数据,夜光数据转面、夜光数据面数据融合、要素转Excel。将相关结果转为Excel,接下来就是在Excel中进行阈值的确定,阈值确定无法通过批量操作,除非采用其他方式,但是那样的学习成本较高,对于参考比较…...

HarmonyOS开发:基于http开源一个网络请求库
前言 网络封装的目的,在于简洁,使用起来更加的方便,也易于我们进行相关动作的设置,如果,我们不封装,那么每次请求,就会重复大量的代码逻辑,如下代码,是官方给出的案例&am…...
【杂记】Ubuntu20.04装系统,安装CUDA等
装20.04系统 安装系统的过程中,ROG的B660G主板,即使不关掉Secure boot也是可以的,不会影响正常安装,我这边出现问题的主要原因是使用了Ventoy制作的系统安装盘,导致每次一选择使用U盘的UEFI启动,就会跳回到…...

040-第三代软件开发-全新波形抓取算法
第三代软件开发-全新波形抓取算法 文章目录 第三代软件开发-全新波形抓取算法项目介绍全新波形抓取算法代码小解 关键字: Qt、 Qml、 抓波、 截获、 波形 项目介绍 欢迎来到我们的 QML & C 项目!这个项目结合了 QML(Qt Meta-Object …...
分享一个基于asp.net的供销社农产品商品销售系统的设计与实现(源码调试 lw开题报告ppt)
💕💕作者:计算机源码社 💕💕个人简介:本人七年开发经验,擅长Java、Python、PHP、.NET、微信小程序、爬虫、大数据等,大家有这一块的问题可以一起交流! 💕&…...
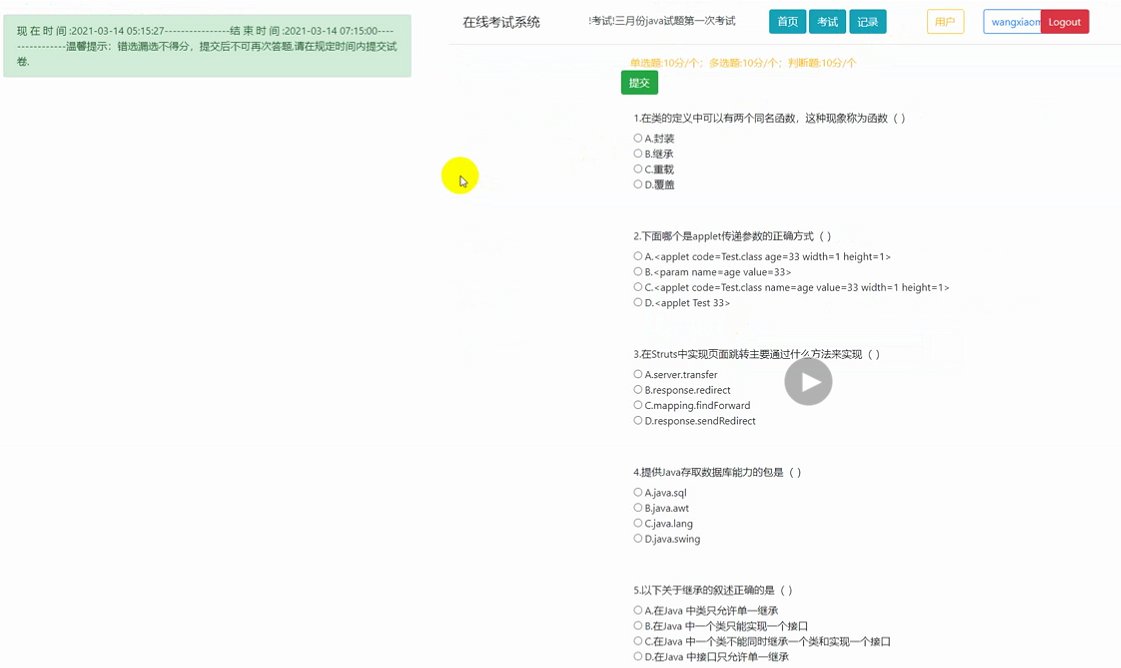
Java基于SpringBoot的线上考试系统
1 摘 要 基于 SpringBoot 的在线考试系统网站,功能模块具有课程管理、成绩管理、教师管理、学生管理、考试管理以及基本信息的管理等,通过将系统分为管理员、授课教师以及学生,从不同的身份角度来对用户提供便利,将科技与教学模式…...

flask socketio 实时传值至html上【需补充实例】
目前版本如下 Flask-Cors 4.0.0 Flask-SocketIO 5.3.6from flask_socketio import SocketIO, emit 跨域问题网上的普通方法无法解决。 参考这篇文章解决 Flask教程(十九)SocketIO - 迷途小书童的Note迷途小书童的Note (xugaoxiang.com) app Flask(__name__) socketio Sock…...
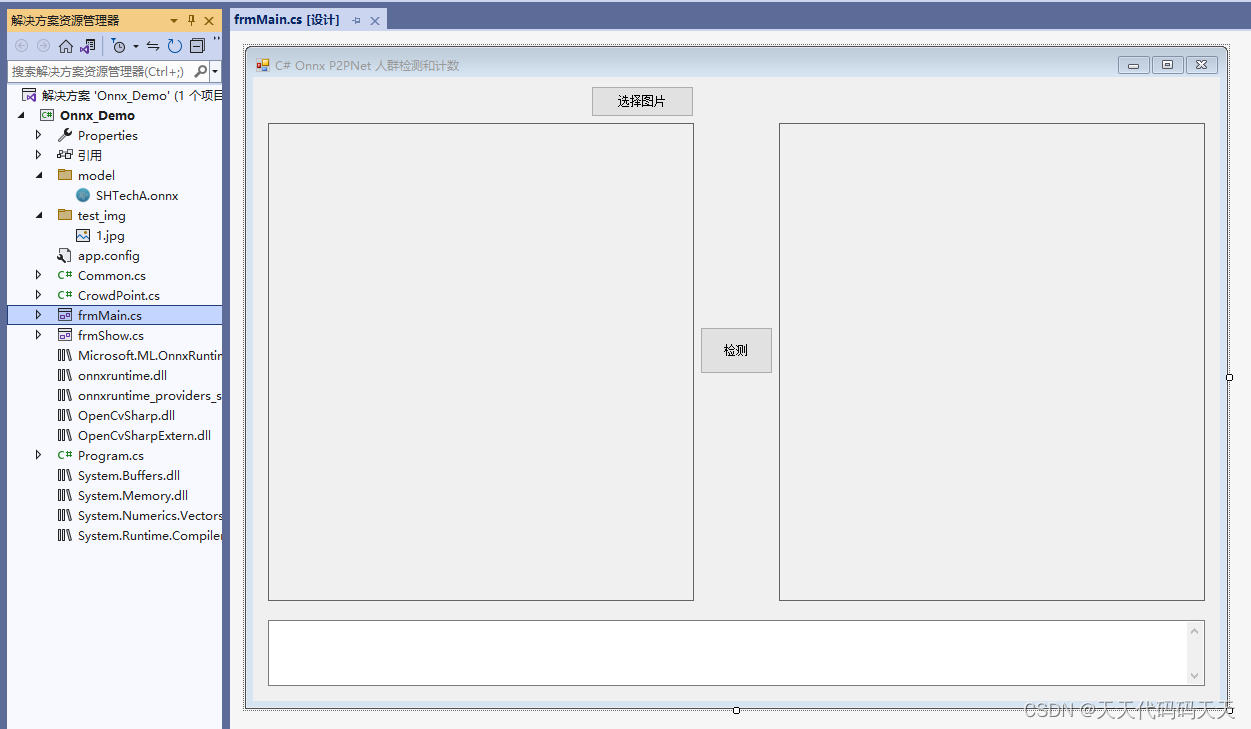
C# Onnx P2PNet 人群检测和计数
效果 项目 代码 using Microsoft.ML.OnnxRuntime; using Microsoft.ML.OnnxRuntime.Tensors; using OpenCvSharp; using System; using System.Collections.Generic; using System.Drawing; using System.Linq; using System.Text; using System.Windows.Forms;namespace Onnx…...
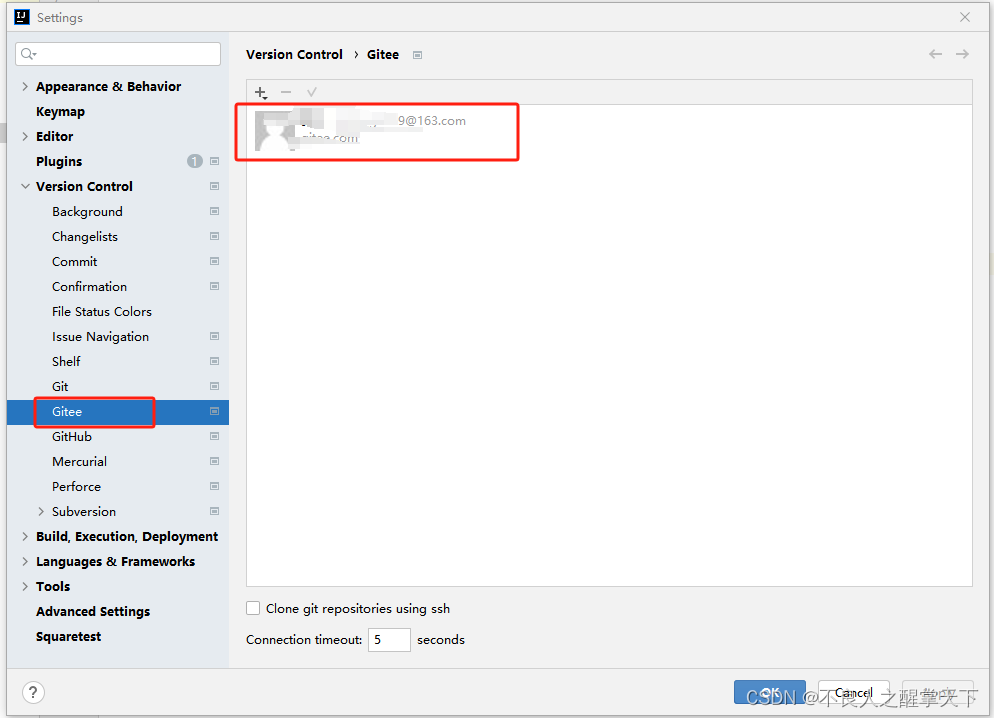
idea提交代码一直提示 log into gitee
解决idea提交代码一直提示 log into gitee问题 文章目录 打开setting->Version control->gitee,删除旧账号,重新配置账号,删除重新登录就好 打开setting->Version control->gitee,删除旧账号,重新配置账号,删除重新登…...

ATECLOUD如何进行电源模块各项性能指标的测试?
ATECLOUD平台进行电源模块各项性能指标的测试是通过以下步骤实现的: 连接测试设备:将测试设备与云计算服务器连接,实现数据采集和远程控制。测试设备包括示波器、电子负载、电源、万用表等,这些设备通过纳米BOX连接到云测试平台上…...

Mysql查询训练——50道题
--1.学生表 Student(SId,Sname,Sage,Ssex) --SId 学生编号,Sname 学生姓名,Sage 出生年月,Ssex 学生性别 --2.课程表 Course(CId,Cname,TId) --CId 课程编号,Cname 课程名称,TId 教师编号 --3.教师表 Teacher(TId,Tname) --TId 教师编号,Tname 教师姓名 --4.成绩表 SC(SId…...
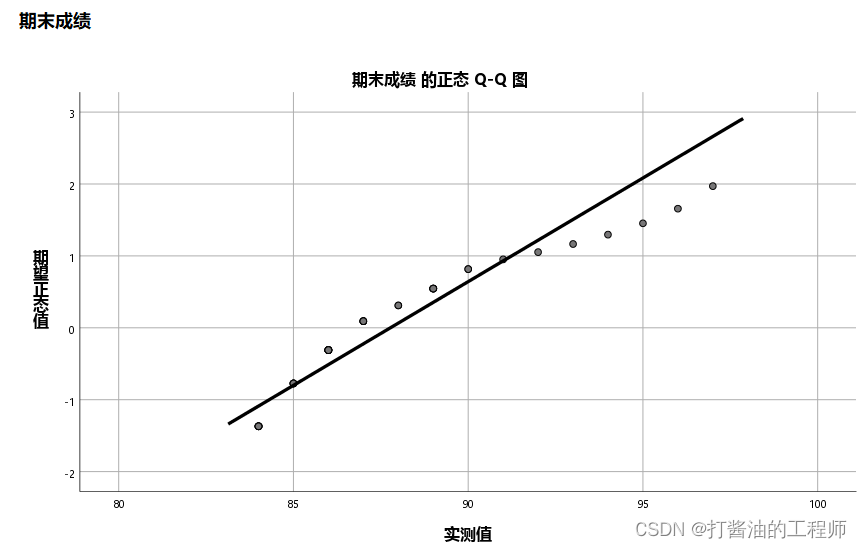
学习笔记|正态分布|图形法|偏度和峰度|非参数检验法|《小白爱上SPSS》课程:SPSS第三讲 | 正态分布怎么检验?看这篇文章就够了
目录 学习目的软件版本原始文档为什么要假设它服从正态分布呢?t检验一、图形法1、频数分布直方图解读 2、正态Q-Q图操作解读 3、正态P-P图SPSS实战操作解读 二、偏度和峰度解读: 三、非参数检验法注意事项 四、规范表达五、小结划重点 学习目的 SPSS第三讲 | 正态…...

Android NDK开发详解之ndk-build 脚本
Android NDK开发详解之ndk-build 脚本 内部原理从命令行调用选项可调试 build 与发布 build要求 ndk-build 脚本使用 NDK 的基于 Make 的构建系统构建项目。我们针对 ndk-build 使用的 Android.mk 和 Application.mk 配置提供了更具体的文档。 内部原理 运行 ndk-build 脚本相…...

应用于智慧矿山的皮带跑偏视频分析AI算法
一、引言 随着科技的发展,人工智能技术已经在各个领域得到广泛应用。而在智慧矿山领域,皮带跑偏视频分析是其中一个重要的应用方向。本文将详细介绍皮带跑偏视频分析AI算法的原理,以期为智慧矿山的发展提供有益的参考。 二、算法原理 1. 视…...

vue3 UI组件优化之element-plus按需导入
如果不在意项目打包体积大小,正常来讲element-plus 是这样用的 import ElementPlus from element-plus //引入样式 import "element-plus/dist/index.css";app.use(ElementPlus);但是呢要是项目就用了几个弹窗提示什么的,全局引入包体积很大 …...
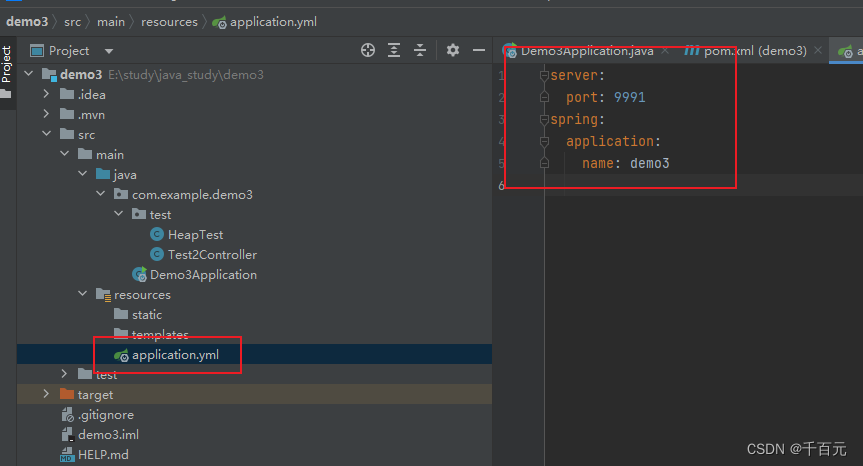
如何创建 Spring Boot 项目
如果有pom.xml有插件异常,可以先删除。 maven配置要配置好 然后yaml,再启动就行 server:port: 9991 spring:application:name: demo3参考 如何创建 Spring Boot 项目_创建springboot项目_良月初十♧的博客-CSDN博客...
【经验分享】openGauss容灾集群搭建
gs_sdr命令代码解读 背景 openGauss推出了容灾架构,相比之前的一个集群主从架构,而容灾架构是两个集群间的数据同步。为了更深入了解其原理,本文试图通过阅读gs_sdr命令相关的代码来学习下相关的各种操作。 1.容灾搭建过程可以参考…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...
