二叉树问题——前中后遍历数组构建二叉树
摘要
利用二叉树的前序,中序,后序,有序数组来构建相关二叉树的问题。
一、构建二叉树题目
105. 从前序与中序遍历序列构造二叉树
106. 从中序与后序遍历序列构造二叉树
889. 根据前序和后序遍历构造二叉树
617. 合并二叉树
226. 翻转二叉树
109. 有序链表转换二叉搜索树
二、构建二叉树问题详解
2.1 前序中序构建二叉树

package Tree;import java.util.HashMap;/*** @BelongsProject: SeniorArchitect-LeetCode* @BelongsPackage: Tree* @Author: zhuangxiaoyan* @CreateTime: 2023-10-25 07:24* @Description: TODO* @Version: 1.0*/
public class 前序中序构建二叉树105 {// 给定的前序和中序遍历构建一个二叉树public TreeNode buildTree(int[] preorder, int[] inorder) {int prelen = preorder.length;int inlen = inorder.length;if (prelen != inlen) {throw new RuntimeException("Imcorrent input data");}HashMap<Integer, Integer> map = new HashMap<>();// 遍历一次中序遍历for (int i = 0; i < inlen; i++) {map.put(inorder[i], i);}// 然后递归调用return buildTree2(preorder, 0, prelen - 1, map, 0, inlen - 1);}private TreeNode buildTree2(int[] preorder, int preleft, int preright, HashMap<Integer, Integer> map, int inleft, int inright) {// 递归的终止条件if (preleft > preright || inleft > inright) {return null;}int rootvalue = preorder[preleft];TreeNode root = new TreeNode(rootvalue);// 获取标int pIndex = map.get(rootvalue);root.left = buildTree2(preorder, preleft + 1, pIndex - inleft + preleft, map, inleft, pIndex - 1);root.right = buildTree2(preorder, pIndex - inleft + preleft + 1, preright, map, pIndex + 1, inright);return root;}class TreeNode {int val;TreeNode left;TreeNode right;public TreeNode(int val) {this.val = val;}}
}
时间与空间复杂度分析
- 时间复杂度:O(n) 最坏的情况就是最左(右)子树 那就需要遍历n-1个元素。
- 空间复杂度:O(1)不需要其他的额外空间来存储元素。
2.2 中序后续构建二叉树

package Tree;import java.util.HashMap;/*** @BelongsProject: SeniorArchitect-LeetCode* @BelongsPackage: Tree* @Author: zhuangxiaoyan* @CreateTime: 2023-10-25 07:25* @Description: TODO* @Version: 1.0*/
public class 后序中序构建二叉树106 {public TreeNode buildTree(int[] inorder, int[] postorder) {int inlen = inorder.length;int postlen = postorder.length;if (inlen != postlen) {throw new RuntimeException("Incurrent input data");}HashMap<Integer, Integer> hashMap = new HashMap<>();for (int i = 0; i < inlen; i++) {hashMap.put(inorder[i], i);}return buildTree2(postorder, 0, postlen - 1, hashMap, 0, inlen - 1);}private TreeNode buildTree2(int[] postorder, int postleft, int postright, HashMap<Integer, Integer> hashMap, int inleft, int inright) {if (postleft > postright || inleft > inright) {return null;}int rootval = postorder[postright];TreeNode root = new TreeNode(rootval);int pIndex = hashMap.get(rootval);root.left = buildTree2(postorder, postleft, pIndex - inleft + postleft - 1, hashMap, inleft, pIndex - 1);root.right = buildTree2(postorder, pIndex - inleft + postleft, postright - 1, hashMap, pIndex + 1, inright);return root;}public class TreeNode {int val;TreeNode left;TreeNode right;TreeNode() {}TreeNode(int val) {this.val = val;}TreeNode(int val, TreeNode left, TreeNode right) {this.val = val;this.left = left;this.right = right;}}
}
时间与空间复杂度分析
- 时间复杂度:O(n) 最坏的情况就是最左(右)子树 那就需要遍历n-1个元素。
- 空间复杂度:O(1)不需要其他的额外空间来存储元素。
2.3 前序后序构建二叉树

- 前序遍历的结果是[1,2,4,5,3,6,7]
- 后序遍历的结果是[4,5,2,6,7,3,1]
- 前序遍历的特点是根节点始终出现在第一位
- 后序遍历的特点是根节点始终出现在最后一位
但是,你会发现仅仅用这些条件还不够,虽然能很快确定根节点了,但是根节点的左子树的范围就没法确定,没法确定左子树范围,也会导致右子树也确定不了。
我们先回顾一下二叉树的前序、后序遍历
二叉树的前序遍历是:
- 打印根节点
- 遍历左子树
- 遍历右子树
二叉树的后序遍历是:
- 遍历左子树
- 遍历右子树
- 打印根节点

前序遍历第一个元素是根节点,后面的那一堆就是左子树,接着是右子树,而后序遍历第一个出现的是左子树,然后是右子树,最后才是根节点,上图中我用橙色标记出了左子树部分,用绿色标记出了右子树部分。
两种遍历方式得到的橙色部分数量是一样的,绿色部分数量也是一样的。所以,我们只要能确定橙色部分的范围,就可以处理左子树了,而左子树范围确定了,那么顺带右子树也就可以搞定了。

- 如果遍历这个左子树
- 前序遍历的结果是[2,4,5]
- 后序遍历的结果是[4,5,2]
我们根据2就可以确定出后序遍历的左子树范围 因为后序遍历的整棵树的结果是[4,5,2,6,7,3,1]
现在我们找到2了,根节点的位置是固定出现在最后的,那么右子树的范围也就可以确定了。
后序遍历数组下标是从0开始的,我们确定了2的位置,还需要+1,这样就得到了整个左子树的个数。
总结一下
- 用前序遍历的第一个元素创建出根节点
- 用前序遍历的第二个元素x,去后序遍历中找对应的下标y,将y+1就能得到左子树的个数了
- 将前序数组,后序数组拆分左右两部分
- 递归的处理前序数组左边、后序数组右边
- 递归的处理前序数组右边、后序数组右边
- 返回根节点
拆分的规则如下(假设得到的左子树数量为left_count)
拆分的前序数组:
- 左半部分[1,left_count+1)
- 右半部分[left_count+1,N)
拆分的后序数组:
- 左半部分[0,left_count)
- 右半部分[left_count,N-1)
package Tree;import org.junit.Test;import java.util.Arrays;/*** @BelongsProject: SeniorArchitect-LeetCode* @BelongsPackage: Tree* @Author: zhuangxiaoyan* @CreateTime: 2023-10-31 20:55* @Description: TODO* @Version: 1.0*/
public class 前序后序构建二叉树 {public class TreeNode {int val;TreeNode left;TreeNode right;TreeNode() {}TreeNode(int val) {this.val = val;}TreeNode(int val, TreeNode left, TreeNode right) {this.val = val;this.left = left;this.right = right;}}public TreeNode constructFromPrePost(int[] pre, int[] post) {if(pre==null || pre.length==0) {return null;}return dfs(pre,post);}private TreeNode dfs(int[] pre,int[] post) {if(pre==null || pre.length==0) {return null;}//数组长度为1时,直接返回即可if(pre.length==1) {return new TreeNode(pre[0]);}//根据前序数组的第一个元素,创建根节点TreeNode root = new TreeNode(pre[0]);int n = pre.length;for(int i=0;i<post.length;++i) {if(pre[1]==post[i]) {//根据前序数组第二个元素,确定后序数组左子树范围int left_count = i+1;//拆分前序和后序数组,分成四份int[] pre_left = Arrays.copyOfRange(pre,1,left_count+1);int[] pre_right = Arrays.copyOfRange(pre,left_count+1,n);int[] post_left = Arrays.copyOfRange(post,0,left_count);int[] post_right = Arrays.copyOfRange(post,left_count,n-1);//递归执行前序数组左边、后序数组左边root.left = dfs(pre_left,post_left);//递归执行前序数组右边、后序数组右边root.right = dfs(pre_right,post_right);break;}}//返回根节点return root;}
}
时间与空间复杂度分析
- 时间复杂度:O(n) 最坏的情况就是最左(右)子树 那就需要遍历n-1个元素。
- 空间复杂度:O(1)不需要其他的额外空间来存储元素。
2.4 合并二叉树

package Tree;/*** @BelongsProject: SeniorArchitect-LeetCode* @BelongsPackage: Tree* @Author: zhuangxiaoyan* @CreateTime: 2023-10-31 22:50* @Description: TODO* @Version: 1.0*/
public class 合并二叉树617 {public class TreeNode {int val;TreeNode left;TreeNode right;TreeNode() {}TreeNode(int val) {this.val = val;}TreeNode(int val, TreeNode left, TreeNode right) {this.val = val;this.left = left;this.right = right;}}public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {if (root1 == null && root2 == null) {return null;}if (root1 == null && root2 != null) {return root2;}if (root1 != null && root2 == null) {return root1;}// 都是kongroot1.val += root2.val;root1.left = mergeTrees(root1.left, root2.left);root1.right = mergeTrees(root1.right, root2.right);return root1;}
}
时间与空间复杂度分析
- 时间复杂度:O(n) 最坏的情况就是遍历二叉树所有元素。
- 空间复杂度:O(1)不需要其他的额外空间来存储元素。
2.5 有序数组构建二叉树

package Tree;/*** @BelongsProject: SeniorArchitect-LeetCode* @BelongsPackage: Tree* @Author: zhuangxiaoyan* @CreateTime: 2023-10-26 08:25* @Description: TODO* @Version: 1.0*/
public class 有序数组构建二叉搜索树108 {public TreeNode sortedArrayToBST(int[] nums) {if (nums.length < 1) {return new TreeNode();}if (nums.length == 1) {return new TreeNode(nums[0]);}TreeNode root = buildTree(nums, 0, nums.length - 1);return root;}private TreeNode buildTree(int[] nums, int left, int right) {if (left > right) {return null;}int mid = left + (right - left) / 2;TreeNode root = new TreeNode(nums[mid]);root.left = buildTree(nums, left, mid - 1);root.right = buildTree(nums, mid + 1, right);return root;}public class TreeNode {int val;TreeNode left;TreeNode right;TreeNode() {}TreeNode(int val) {this.val = val;}TreeNode(int val, TreeNode left, TreeNode right) {this.val = val;this.left = left;this.right = right;}}
}
时间与空间复杂度分析
- 时间复杂度:O(n) 最坏的情况就是二叉树所有的元素。
- 空间复杂度:O(1)不需要其他的额外空间来存储元素。
2.6 翻转二叉树
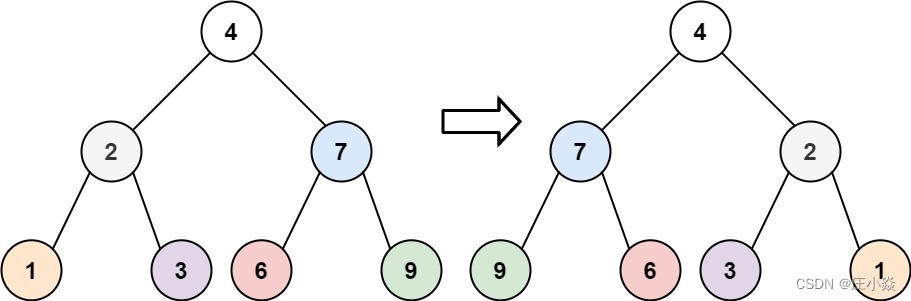
package Tree;/*** @BelongsProject: SeniorArchitect-LeetCode* @BelongsPackage: Tree* @Author: zhuangxiaoyan* @CreateTime: 2023-10-24 22:47* @Description: TODO* @Version: 1.0*/
public class 二叉树翻转226 {public TreeNode invertTree(TreeNode root) {if (root == null) {return root;}// 交换左右子树TreeNode tmp = root.right;root.right = root.left;root.left = tmp;// 递归的调用左右子树invertTree(root.left);invertTree(root.right);return root;}public TreeNode invertTree2(TreeNode root) {if (root == null) {return root;}// 递归左右的遍历invertTree(root.left);invertTree(root.right);// 中遍历TreeNode tmp = root.left;root.left = root.right;root.right = tmp;return root;}public TreeNode invertTree3(TreeNode root) {if (root == null) {return root;}// 递归左右的遍历invertTree3(root.left);// 中遍历TreeNode tmp = root.left;root.left = root.right;root.right = tmp;invertTree3(root.left); // 注意 这里依然要遍历左孩子,因为中间节点已经翻转了return root;}public class TreeNode {int val;TreeNode left;TreeNode right;TreeNode() {}TreeNode(int val) {this.val = val;}TreeNode(int val, TreeNode left, TreeNode right) {this.val = val;this.left = left;this.right = right;}}}
时间与空间复杂度分析
- 时间复杂度:O(n) 最坏的情况就是遍历所有元素。
- 空间复杂度:O(1)不需要其他的额外空间来存储元素。
博文参考
https://leetcode.cn/circle/discuss/E3yavq/#%E6%A0%91%E4%B8%8E%E4%BA%8C%E5%8F%89%E6%A0%91%E7%AF%87
相关文章:

二叉树问题——前中后遍历数组构建二叉树
摘要 利用二叉树的前序,中序,后序,有序数组来构建相关二叉树的问题。 一、构建二叉树题目 105. 从前序与中序遍历序列构造二叉树 106. 从中序与后序遍历序列构造二叉树 889. 根据前序和后序遍历构造二叉树 617. 合并二叉树 226. 翻转二…...
)
Java保留n位小数的方法(超简洁)
要输出double类型保留n位小数的几种方法如下: 我们以保留6位小数为例 方法一:使用DecimalFormat类 import java.text.DecimalFormat;public class Main {public static void main(String[] args) {double number 3.141592653589793;DecimalFormat df …...

JavaEE-博客系统1(数据库和后端的交互)
本部分内容包括网站设计总述,数据库和后端的交互; 数据库操作代码如下: -- 编写SQL完成建库建表操作 create database if not exists java_blog_system charset utf8; use java_blog_system; -- 建立两张表,一个存储博客信息&am…...
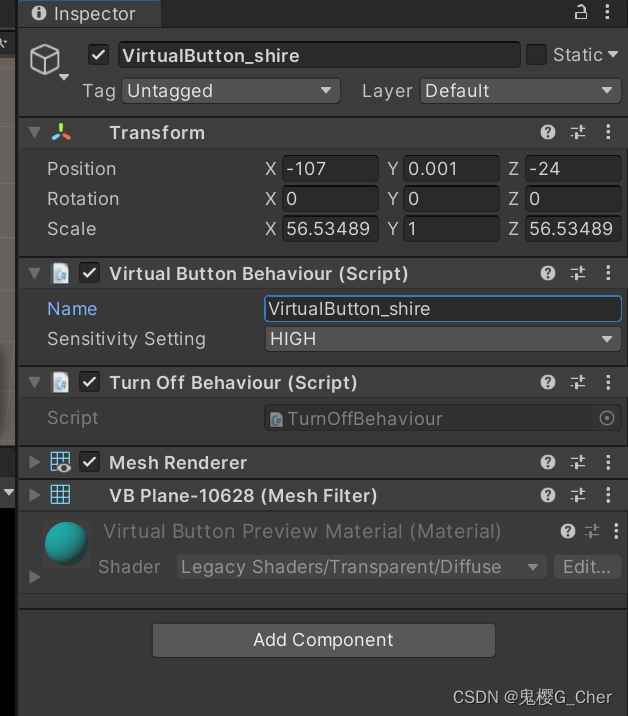
【unity/vufornia】Duplicate virtual buttons with name.../同一个ImageTarget上多个按钮失灵
问题:在同一个ImageTarget上添加多个按钮时无法触发对应按钮的事件。 解决过程: 1.查看报错:“Duplicate virtual buttons with name...”这一行,顾名思义,命名重复。 2.英文搜索到以下文章,应该在inspe…...

Apache ActiveMQ 远程代码执行漏洞复现(CNVD-2023-69477)
Apache ActiveMQ 远程代码执行RCE漏洞复现(CNVD-2023-69477) 上周爆出来的漏洞,正好做一下漏洞复现,记录一下 1.漏洞描述 Apache ActiveMQ 中存在远程代码执行漏洞,具有 Apache ActiveMQ 服务器TCP端口ÿ…...

项目管理-科学管理基础-线性规划介绍及例题
项目管理中的线性规划是什么? 在项目管理中,线性规划是一种数学建模和优化技术,用于解决资源分配和进度规划的问题。线性规划的目标是在给定的资源限制下,找到最佳的资源分配方案,以满足项目的需求并优化特定的目标,如成本最小化或时间最短化。 线性规划的基本元素包括…...
如何利用自定义数据对象(元数据)实现全场景身份数据治理
在数字化时代背景下,5G、云计算、大数据、物联网、人工智能等技术的发展,为企业数据管理提供了基础技术支撑。数字化浪潮推动企业快速升级迭代,在数据管理和数字化转型过程中,企业内部的数据情况常常错综复杂,并伴随着…...
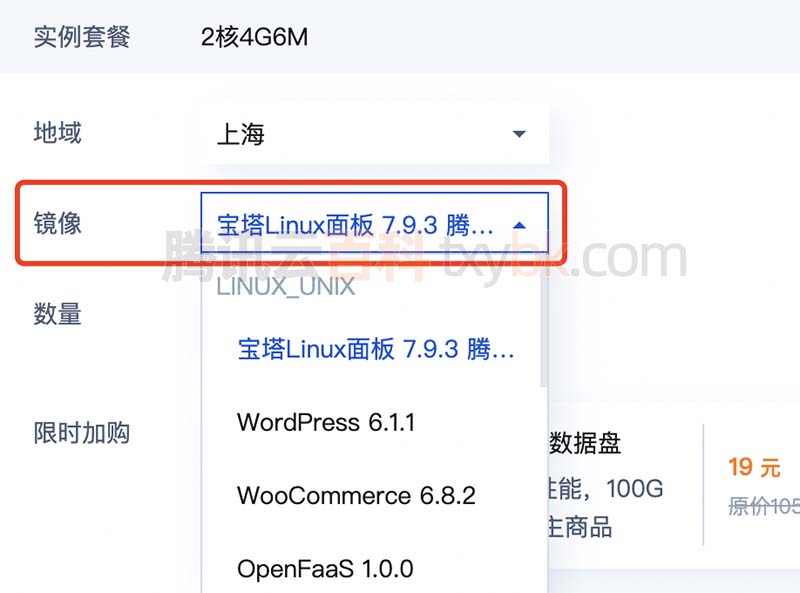
腾讯云轻量级服务器哪个镜像比较好?
腾讯云轻量应用服务器镜像是什么?镜像就是操作系统,轻量服务器镜像系统怎么选择?如果是用来搭建网站腾讯云百科txybk.com建议选择选择宝塔Linux面板腾讯云专享版,镜像系统根据实际使用来选择,腾讯云百科来详细说下腾讯…...

SC密封件的材料成分
SC密封件也称为轴密封件,是许多机械系统中的关键组件,提供防止润滑剂泄漏和污染物进入的屏障。但SC密封件是由什么材料制成的呢? SC密封型材由带有橡胶涂层的单个金属保持架和带有集成弹簧的主密封唇组成。这种材料的组合为密封件提供了其基本特性&…...
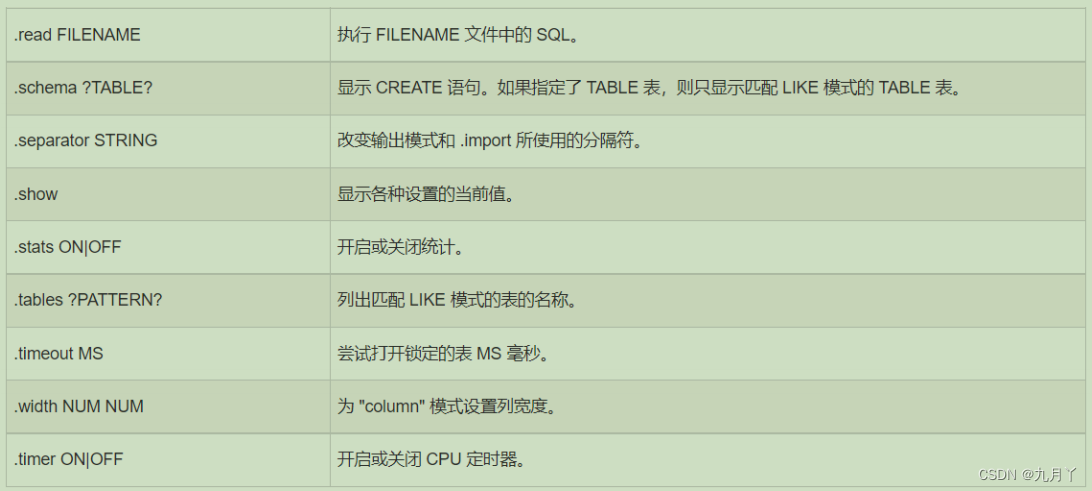
常用 sqlite3 命令
本次将向您讲解 SQLite 编程人员所使用的简单却有用的命令。这些命令被称为 SQLite 的点命令,这些命令的不同之处在于它们不以分号 ; 结束。 让我们在命令提示符下键入一个简单的 sqlite3 命令,在 SQLite 命令提示符下,您可以使 用各种 …...
SpringMVC Day 08 : 文件上传下载
前言 文件上传和下载是 Web 开发中的重要环节,但它们往往不那么容易实现。幸运的是,Spring MVC 提供了一套简单而又强大的解决方案,让我们可以专注于业务逻辑,而不必过多关注底层的文件处理细节。 在本篇博客中,我们…...
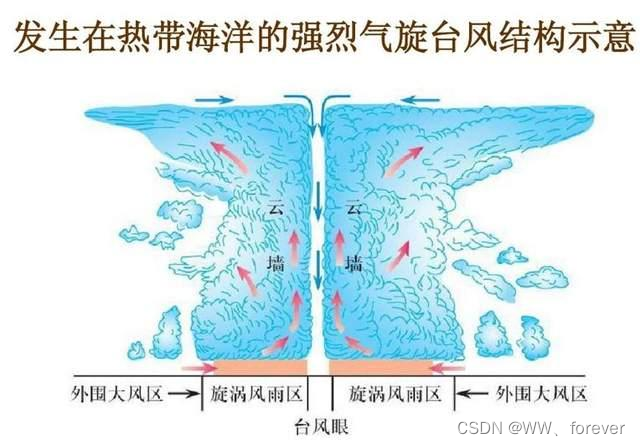
【热带气旋】基本介绍:定义、标准、结构等
热带气旋基本介绍 热带气旋(Tropical Cyclone, TC)1 热带气旋定义2 热带气旋标准2.1 热带低压(Tropical Depression)2.2 热带风暴(Tropical storm)2.3 强热带风暴(Severe tropical storm&#x…...
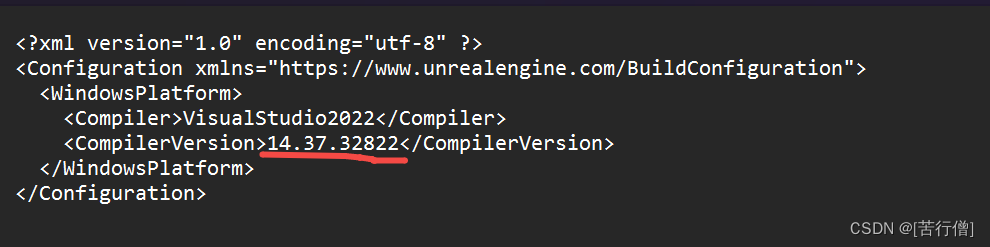
ue5 右击.uproject generator vs project file 错误
出现如下错误 Unable to find valid 14.31.31103 C toolchain for VisualStudio2022 x64 就算你升级了你的 vs installer 也不好使 那是因为 在C:\Users\{YourUserName}\AppData\Roaming\Unreal Engine\UnrealBuildTool\BuildConfiguration.xml 这个缓存配置文件中写死了 14…...
0X01
打开题目 点了几下跳出一个新的页面 点击secret 在上一个页面查看源代码,出现action.php然后点击之后就会在地址栏里面出现end.php 抓包看看,出现secr3t.php huidao开始的页面,访问看看 这是一个PHP脚本,以HTML标签开头。该脚本包…...
centos7 配置搭建 wordpress 博客
环境配置 系统:centos7 CPU:2核 内存:4G 硬盘:40G 一、登录云服务器器 1.单击实例--实例名称 2. 选择安全组页签,单击安全组操作列的管理规则, 3.在入方向添加需要放行的端口。本教程中,在安全组入方向…...

掌握Android自定义View与独家优化技巧
在Android应用开发中,自定义View是一种强大的工具,可以帮助你创建独特的用户界面元素。本文将详细介绍如何创建自定义View,并提供优化技巧,以确保你的自定义View在性能和用户体验方面表现出色。 什么是自定义View 自定义View是A…...
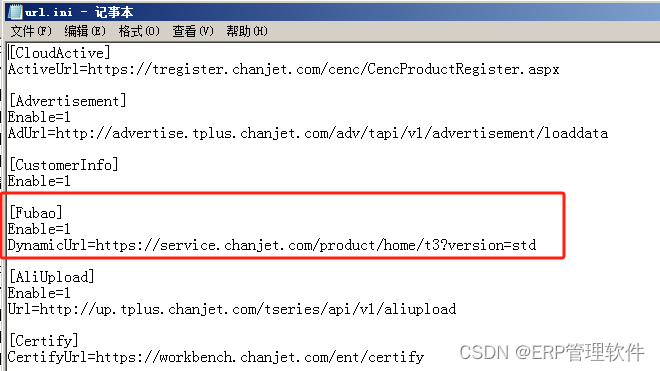
【T3】彻底关闭服宝
【问题描述】 畅捷通T3登录后, 右下角会出现服宝窗口,需要手工退出。 但是每次重新登录账套后都会出现,非常烦;并且界面空白。 【解决方法】 在软件的安装目录下\UFSMART\Portal,找到【url.ini】文件。 用记事本打开…...

P2359 三素数数 , 线性dp
题目背景 蛟川书院的一道练习题QAQ 题目描述 如果一个数的所有连续三位数字都是大于100的素数,则该数称为三素数数。比如113797是一个6位的三素数数。 输入格式 一个整数n(3 ≤ n ≤ 10000),表示三素数数的位数。 输出格式 …...

【c语言】用C语言设计一个环形缓冲区。当环形缓冲区有一半占用未处理时,提示使用了50%.
InsCode AI创作助手 #include <stdio.h> #include <stdlib.h>#define BUFFER_SIZE 10int buffer[BUFFER_SIZE]; // 环形缓冲区数组 int readIndex 0; // 缓冲区读取索引 int writeIndex 0; // 缓冲区写入索引 int count 0; // 缓冲区占用计数器void enqueue(in…...
Selenium的显性等待(元素定位))
Python的web自动化学习(四)Selenium的显性等待(元素定位)
引言: Selenium的显性等待,其常用的定位方法介绍,后面持续更细具体用法 示例如下: <input type"text" class"s_ipt" name"wd" id"kw" maxlength"100" autocomplete"…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...

医疗AI模型可解释性编程研究:基于SHAP、LIME与Anchor
1 医疗树模型与可解释人工智能基础 医疗领域的人工智能应用正迅速从理论研究转向临床实践,在这一过程中,模型可解释性已成为确保AI系统被医疗专业人员接受和信任的关键因素。基于树模型的集成算法(如RandomForest、XGBoost、LightGBM)因其卓越的预测性能和相对良好的解释性…...

麒麟系统使用-进行.NET开发
文章目录 前言一、搭建dotnet环境1.获取相关资源2.配置dotnet 二、使用dotnet三、其他说明总结 前言 麒麟系统的内核是基于linux的,如果需要进行.NET开发,则需要安装特定的应用。由于NET Framework 是仅适用于 Windows 版本的 .NET,所以要进…...

暴雨新专利解决服务器噪音与性能悖论
6月1日,我国首部数据中心绿色化评价方面国家标准《绿色数据中心评价》正式实施,为我国数据中心的绿色低碳建设提供了明确指引。《评价》首次将噪音控制纳入国家级绿色评价体系,要求从设计隔声结构到运维定期监测实现闭环管控,加速…...
