P2359 三素数数 , 线性dp
题目背景
蛟川书院的一道练习题QAQ
题目描述
如果一个数的所有连续三位数字都是大于100的素数,则该数称为三素数数。比如113797是一个6位的三素数数。
输入格式
一个整数n(3 ≤ n ≤ 10000),表示三素数数的位数。
输出格式
一个整数,表示n位三素数的个数m,要求输出m除以10^9 + 9的余数。
输入输出样例
输入 #1复制
4
输出 #1复制
204
说明/提示
区域动归QAQ
解析:
第一次的错误做法:
f[i] 表示前 i 为的三素数的个数,f[i]=f[i-3]*t+f[i-2]+f[i-1], t 表示 1 到 1e3 内的素数的个数
这个做法是错误的,题目的意思应该是任意三个连续的数组成的三位数一定是素数,上述的做法只考虑了当前连续的三个数,而非任意任意三个连续的数,所以上述做法是错误的
正确的做法:
最容易,最直接的划分方式:f[i][j][k][l] 表示前 i 位,最近的三位数,百位为 j ,十位为 k,个位为 l 的三素数个的个数
状态转移方程:f[i][j][k][l]=(f[i-1][k][l][p]+f[i][j][k][l])%mod;
初始化 f[3][j][k][l]=1;
时间复杂度为O(1e3*n),最坏情况为 1e8
优化:
我们可以发现上述划分集合的最后一维是可以省去的:
f[i][j][k] 表示: 最近的三位数,百位为 j ,十位为 k,个位为 l 的三素数个的个数,这里 l 省去了,
f[i][j][k]=(f[i][j][k]+f[i-1][k][l])%mod;
初始化可以不改变,也可以改为:f[2][j][k]=1;
优化前的代码:
#include<iostream>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<math.h>
#include<map>using namespace std;
typedef long long LL;
const int N = 1e4 + 3, M = 1e3,mod=1e9+9;
int n;
LL f[N][11][11][11];
int an[M];
vector<int>prime;void init() {an[1] = 1;for (int i = 2; i < M; i++) {if (an[i] == 0) {prime.push_back(i);}for (int j = 0; j < prime.size() && prime[j] * i < M; j++) {an[prime[j] * i] = 1;}}
}int main() {init();cin >> n;for (int j = 1; j <= 9; j++) {for (int k = 0; k <= 9; k++) {for (int l = 0; l <= 9; l++) {f[3][j][k][l] = 1;}}}int t=0,tt=0;for (int i = 4; i <= n; i++) {for (int j = 1; j <= 9; j++) {for (int k = 0; k <= 9; k++) {for (int l = 0; l <= 9; l++) {for (int p = 0; p <= 9; p++) {t = j * 100 + k * 10 + l;tt = k * 100 + l * 10 + p;if (!an[t]&&!an[tt]) {f[i][j][k][l] = (f[i - 1][k][l][p] + f[i][j][k][l])%mod;}}}}}}LL ans = 0;for (int j = 0; j <= 9; j++) {for (int k = 0; k <= 9; k++) {for (int l = 1; l <= 9; l++) {t = j * 100 + k * 10 + l;if (!an[t])ans = (ans + f[n][j][k][l]) % mod;}}}cout << ans << endl;return 0;
}优化后的代码
#include<iostream>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<math.h>
#include<map>using namespace std;
typedef long long LL;
const int N = 1e4 + 3, M = 1e3, mod = 1e9 + 9;
int n;
LL f[N][11][11];
int an[M];
vector<int>prime;void init() {an[1] = 1;for (int i = 2; i < M; i++) {if (an[i] == 0) {prime.push_back(i);}for (int j = 0; j < prime.size() && prime[j] * i < M; j++) {an[prime[j] * i] = 1;}}
}int main() {init();cin >> n;for (int j = 0; j <= 9; j++) {for (int k = 0; k <= 9; k++) {f[2][j][k] = 1;}}int t = 0, tt = 0;for (int i = 3; i <= n; i++) {for (int j = 1; j <= 9; j++) {for (int k = 0; k <= 9; k++) {for (int l = 0; l <= 9; l++) {t = j * 100 + k * 10 + l;if (!an[t]) {f[i][j][k] = (f[i - 1][k][l] + f[i][j][k]) % mod;}}}}}LL ans = 0;for (int j = 0; j <= 9; j++) {for (int k = 0; k <= 9; k++) {ans = (ans + f[n][j][k]) % mod;}}cout << ans << endl;return 0;
}相关文章:

P2359 三素数数 , 线性dp
题目背景 蛟川书院的一道练习题QAQ 题目描述 如果一个数的所有连续三位数字都是大于100的素数,则该数称为三素数数。比如113797是一个6位的三素数数。 输入格式 一个整数n(3 ≤ n ≤ 10000),表示三素数数的位数。 输出格式 …...

【c语言】用C语言设计一个环形缓冲区。当环形缓冲区有一半占用未处理时,提示使用了50%.
InsCode AI创作助手 #include <stdio.h> #include <stdlib.h>#define BUFFER_SIZE 10int buffer[BUFFER_SIZE]; // 环形缓冲区数组 int readIndex 0; // 缓冲区读取索引 int writeIndex 0; // 缓冲区写入索引 int count 0; // 缓冲区占用计数器void enqueue(in…...
Selenium的显性等待(元素定位))
Python的web自动化学习(四)Selenium的显性等待(元素定位)
引言: Selenium的显性等待,其常用的定位方法介绍,后面持续更细具体用法 示例如下: <input type"text" class"s_ipt" name"wd" id"kw" maxlength"100" autocomplete"…...

X3DAudio1_7.dll是什么,解决计算机找不到X3DAudio1_7.dll文件的方法
作为一位程序员,我深知x3daudio1_7.dll丢失对电脑用户的影响。这个文件是DirectX的一个组件,它负责处理音频输出和输入。当这个文件丢失时,可能会导致电脑无法正常播放音频,甚至出现蓝屏等问题。那么,面对这个问题&…...
 方法有关RGB颜色设置详解)
【Python】海龟图turtle.color() 方法有关RGB颜色设置详解
在Turtle模块中,turtle.color()函数用于设置画笔和填充颜色,你可以使用RGB颜色码作为参数。RGB颜色码由三个数字组成,分别代表红色(R),绿色(G)和蓝色(B)的分量…...

中科院上高院,协鑫,和数“能源数字化智能管控”合作项目开启
10月27日,上海和数软件有限公司与协鑫综合能源服务有限公司、中国科学院上海高等研究院签署了《关于“能源数字化智能管控”开发与应用框架合作协议》。 这也标志着新疆协鑫智慧能源有限公司数字化智能提升项目——数字孪生项目正式启动。 根据协议,三方…...
在Mac上安装MongoDB 5.0
MongoDB 5.0安装 1、环境描述 操作系统:macOS 14.0 (23A344) 2、安装MongoDB 2.1、tar解压包安装 下载地址:Download MongoDB Community Server | MongoDB 创建一个目录,以便数据库将文件放入其中。(默认情况下,数据…...

手把手教你如何实现TNAS与云盘之间的无缝同步技巧
嘿,铁粉们! 云盘的下载速度总是让我们抓耳挠腮 数据安全隐私问题让人担心不已 但在购入NAS之前 众多数据存放在云盘里 同时也想把NAS的数据备份在云盘里 实现备份321法则? 不用烦恼 铁威马来帮忙 无需其他多余操作 只要下载CloudSyn…...

【约会云栖】从初中至大学,我见证了科技变革的历程。
前言 提起阿里云开发者大会, 你一定会觉得陌生;但提起云栖大会,你又会耳熟能详。实际上,云栖大会的前身就是阿里云开发者大会,2015年,它永久落户在杭州市西湖区云栖小镇。 2023年10月31日至11月2日…...

【MySQL索引与优化篇】索引优化与查询优化
索引优化与查询优化 文章目录 索引优化与查询优化1. 概述2. 索引失效案例3. 关联查询优化3.1 Join语句原理3.2 Simple Nested-Loop Join(简单嵌套循环连接)3.3 Index Nested-Loop Join(索引嵌套循环连接)3.4 Block Nested-Loop Jo…...

DevChat:VSCode中基于大模型的AI智能编程助手
#AI编程助手哪家好?DevChat“真”好用# 文章目录 1. 前言2. 安装2.1 注册新用户2.2 在VSCode中安装DevChat插件2.3 设置Access Key 3. 实战使用4. 总结 1. 前言 DevChat是由Merico公司精心打造的AI智能编程助手。它利用了最先进的大语言模型技术,像人类…...

Scrum master的职责
首先,Scrum master负责建立Scrum团队。同时Scrum master要帮助团队(甚至大到公司)中的每个成员理解Scrum理论和实践。 Scrum master还需要有很强的软技能,用于指导Scrum团队。Scrum master要对Scrum团队的成功负责任,…...

数据结构:算法(特性,时间复杂度,空间复杂度)
目录 1.算法的概念2.算法的特性1.有穷性2.确定性3.可行性4.输入5.输出 3.好算法的特质1.正确性2.可读性3.健壮性4.高效率与低存储需求 4.算法的时间复杂度1.事后统计的问题2.复杂度表示的计算1.加法规则2.乘法规则3.常见函数数量级比较 5.算法的空间复杂度1.程序的内存需求2.例…...

SaaS 出海,如何搭建国际化服务体系?(一)
防噎指南:这可能是你看到的干货含量最高的 SaaS 出海经验分享,请准备好水杯,放肆食用(XD。 当越来越多中国 SaaS 企业选择开启「国际化」副本,出海便俨然成为国内 SaaS 的新角斗场。 LigaAI 观察到,出海浪…...

数据结构与算法-(7)---栈的应用拓展-前缀表达式转换+求值
🌈write in front🌈 🧸大家好,我是Aileen🧸.希望你看完之后,能对你有所帮助,不足请指正!共同学习交流. 🆔本文由Aileen_0v0🧸 原创 CSDN首发🐒 如…...

泛型的使用
泛型是一种Java编程语法,它允许我们编写支持多种数据类型的通用类、方法和接口。使用泛型可以使代码更通用、更灵活、更健壮,并提高代码的重用性。 在Java中,泛型的语法使用尖括号<>和类型参数来定义。例如,我们可以定义一…...

docker导致远程主机无法访问,docker网段冲突导致主机网络异常无法访问
背景: 公司分配的虚拟机是172网段的,在上面部署了docker、docker-compose、mysql、redis,程序用docker-compose管理,也平稳运行了一个多周,某天用FinalShell连主机重启docker容器,忽然断开连接,然后虚拟机就…...
Selenium的显性、隐形等待)
Python的web自动化学习(三)Selenium的显性、隐形等待
引言: WebDriver的显性等待和隐形等待是用于在测试过程中等待元素加载或操作完成的两种等待方式。了解此两种方式是为后面自动化找到适合的方法去运用 显性等待(Explicit Wait) 显性等待是通过使用WebDriverWait类和ExpectedConditions类来…...

Linux--文件操作
1.什么是文件 对于文件来说,文件文件内容文件属性;对于文件来说,只有两种操作,对内容的修改和对文件属性的修改,这就是文件的范畴。 对于存放在磁盘上的文件,我们需要通过进程来进行访问,访问文…...
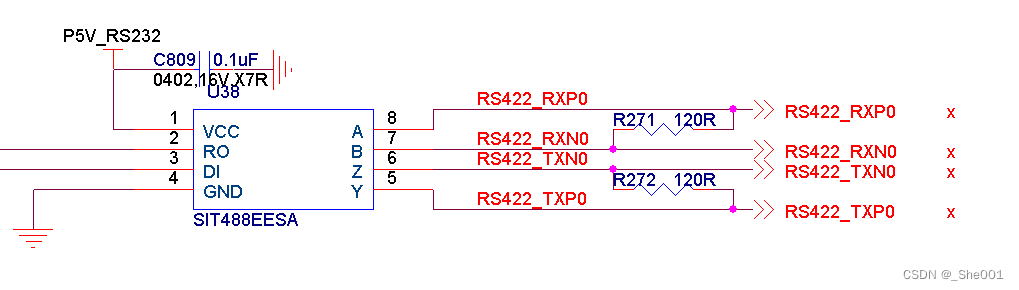
硬件知识积累 RS422接口
1. RS422 基本介绍 EIA-422(过去称为RS-422)是一系列的规定采用4线,全双工,差分传输,多点通信的数据传输协议。它采用平衡传输采用单向/非可逆,有使能端或没有使能端的传输线。和RS-485不同的是EIA-422不允…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...
