人工智能基础_机器学习011_梯度下降概念_梯度下降步骤_函数与导函数求解最优解---人工智能工作笔记0051

然后我们来看一下梯度下降,这里先看一个叫
无约束最优化问题,,值得是从一个问题的所有可能的备选方案中选最优的方案,
我们的知道,我们的正态分布这里,正规的一个正态分布,还有我们的正规方程,他的这个x,是正规的,比如上面画的这个曲线,他的这个x,就是大于0的对吧,而现实生活中,
我们x的值可能是各种各样的没有约束的,基于没有约束的,这个问题..
我们来求导数,对y求导数得到,曲线的斜率,就叫做梯度下降
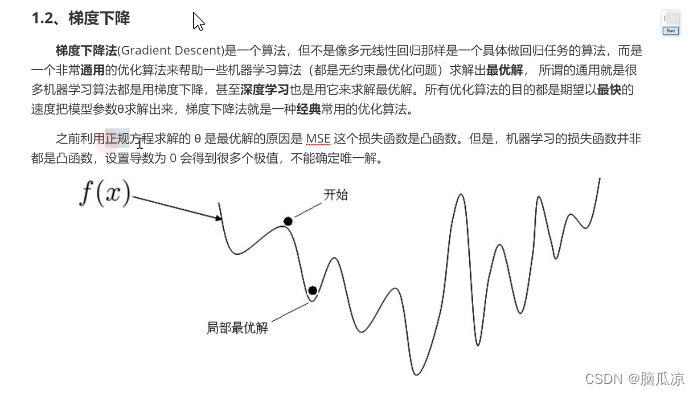
继续看,我们要找导数为0的,那么可以看到,底部
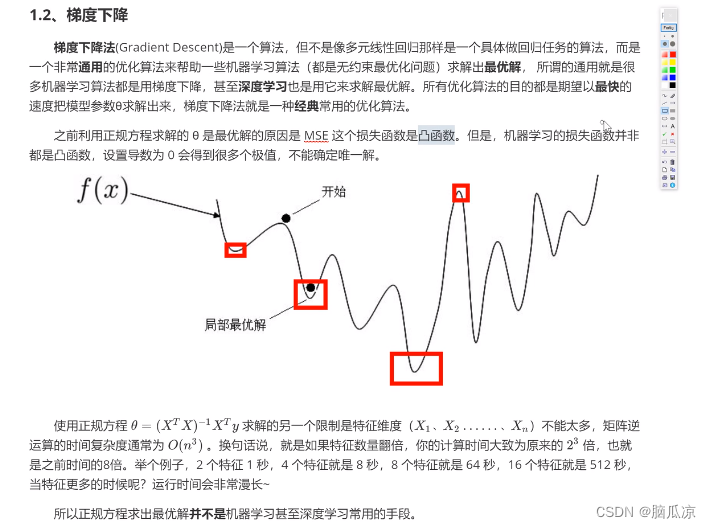
可以看到底部,和曲线的顶部都是斜率为0,导数为0对吧,但是
好在我们已经验证了,我们的最小二乘法,正态分布,对应的 是一个 开口向上的函数
所以我们找到的肯定是最低点对吧.

因为我们使用正规方程一次进行求解的话,花费的时间很长,可以看上面的说明.
所以我们只需要,令导数为0,然后这个就是斜率为0,求这个时候的seta是多少,其实就是模型w对吧
梯度下降法,其实就是,一点点去逼近这个最优解</
相关文章:

人工智能基础_机器学习011_梯度下降概念_梯度下降步骤_函数与导函数求解最优解---人工智能工作笔记0051
然后我们来看一下梯度下降,这里先看一个叫 无约束最优化问题,,值得是从一个问题的所有可能的备选方案中选最优的方案, 我们的知道,我们的正态分布这里,正规的一个正态分布,还有我们的正规方程,他的这个x,是正规的,比如上面画的这个曲线,他的这个x,就是大于0的对吧,而现实生活…...

开放式耳机能保护听力吗,开放式耳机跟骨传导耳机哪个更好?
如果从严格意义上来讲的话,开放式耳机中的骨传导耳机是能保护听力,现如今的开放式耳机是一个统称,将所有不入耳的类目全部规划到一块。因此在开放式耳机中存在着一些耳机是只能够保持周边环境音,而不是保护听力的。 下面让我来给…...
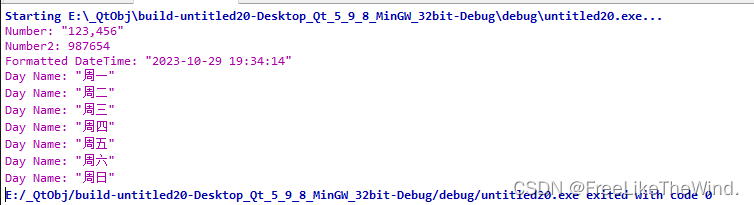
【Qt之QLocale】使用
描述 QLocale类可以在多种语言之间进行数字和字符串的转换。 QLocale类在构造函数中使用语言/国家对进行初始化,并提供类似于QString中的数字转字符串和字符串转数字的转换函数。 示例: QLocale egyptian(QLocale::Arabic, QLocale::Egypt);QString s1 …...
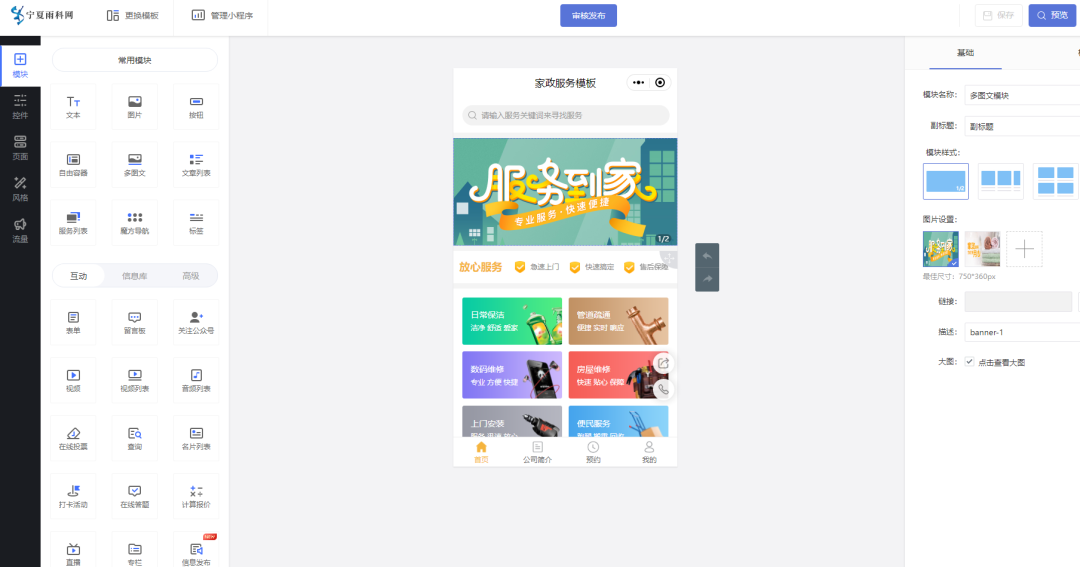
维修服务预约小程序的效果如何
生活服务中维修项目绝对是需求量很高的,如常见的保洁、管道疏通、数码维修、安装、便民服务等,可以说每天都有生意,而对相关维修店企业来说,如何获得更多生意很重要。 接下来让我们看看通过【雨科】平台制作维修服务预约小程序能…...
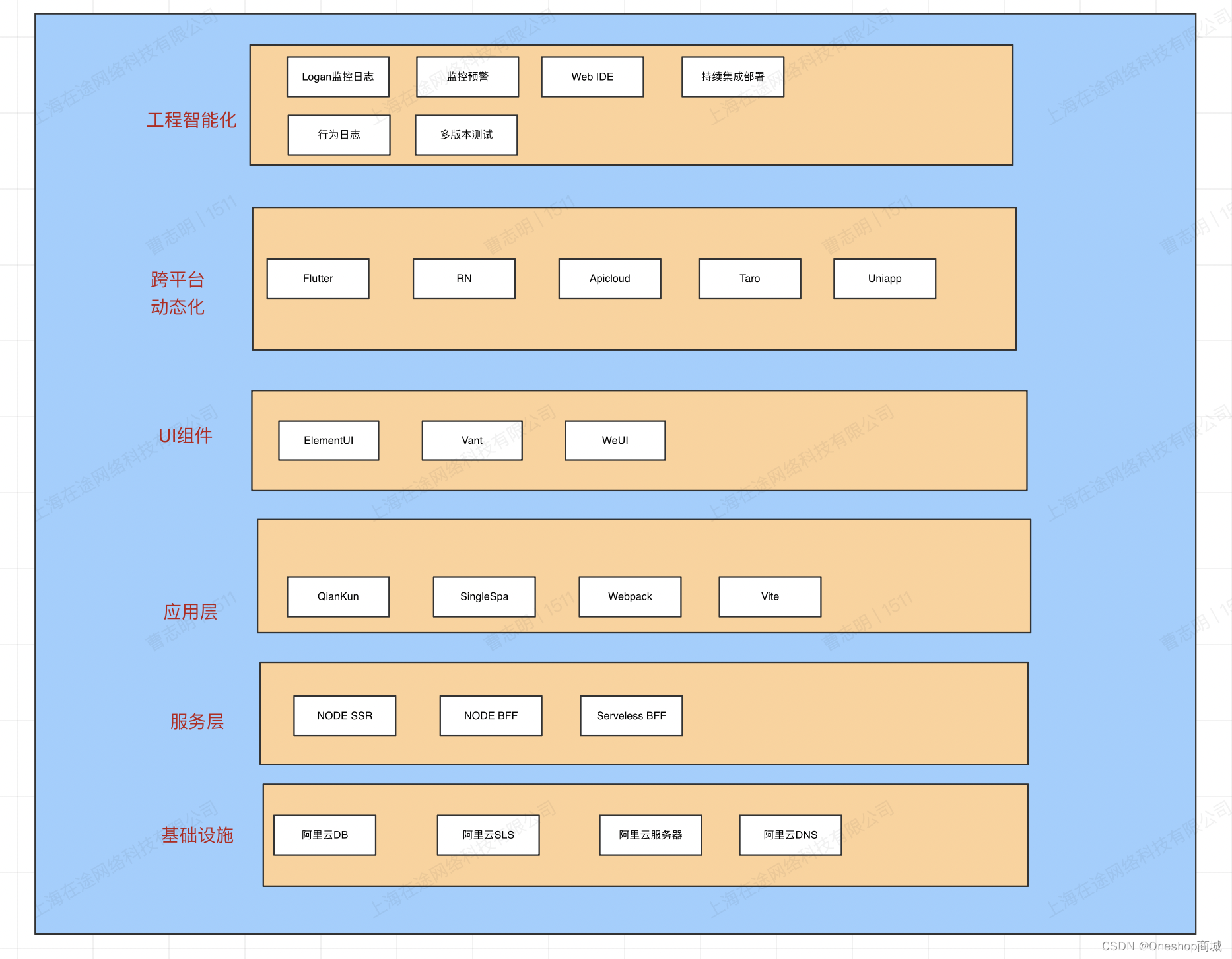
前端架构体系调研整理汇总
1.公司研发人数与前端体系 小型创业公司 前端人数: < 3 人 产品类型: 产品不是非常成熟,比较新颖。 项目流程:不完善,快、紧促,没有固定的时间排期。 技术栈: 没有历史包袱,技…...

DrawerLayout的点击事件会穿透到底部,如何拦截?
DrawerLayout实现侧后,发现了一个问题。点击DrawerLayout的画面,会触发覆盖的底层页面的控件。由此说明点击事件穿透到了底部。但是我只需要触发抽屉布局里的控件,不想触发底层被覆盖的看不见的按钮,由此我想到的时让抽屉页面拦截…...
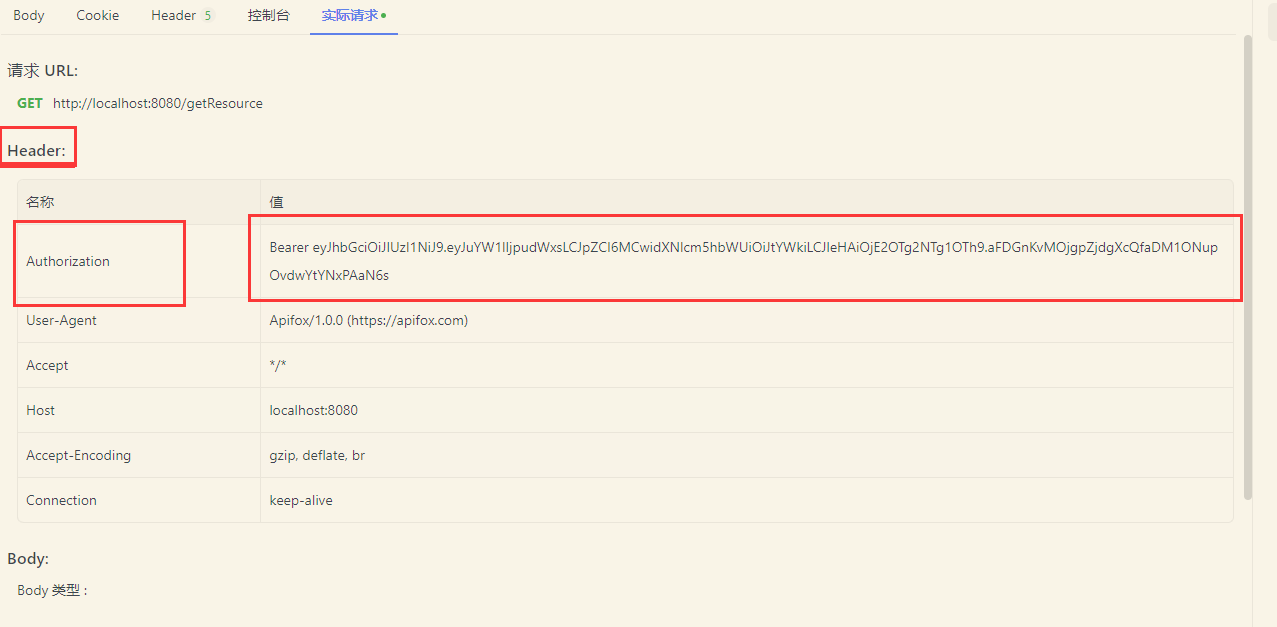
在Spring boot中 使用JWT和过滤器实现登录认证
在Spring boot中 使用JWT和过滤器实现登录认证 一、登录获得JWT 在navicat中运行如下sql,准备一张user表 -- ---------------------------- -- Table structure for t_user -- ---------------------------- DROP TABLE IF EXISTS t_user; CREATE TABLE t_user (id int(11) …...

天堂2如何对版本里面的内容进行修改
天堂2写装备属性的问题 早一点的版本属性都是写在armor文件夹 xml档里,不再写armor里了 armor文件夹里只有防御 HP MP增加量,套装的属性都用一个技能形式写在 skills里了 在配合数据库里一个叫armorsets实现套装属性,拿皇家套做说明。 id 43…...
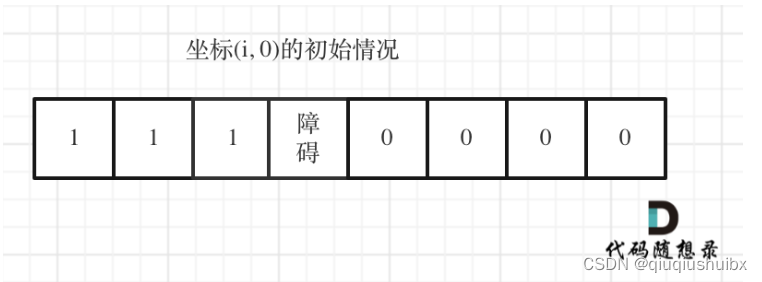
代码随想录Day33 LeetCode T62不同路径 LeetCode T63 不同路径II
前言 动规五部曲 1.确定dp数组含义 2.确定递推公式 3.初始化数组 4.确定遍历方式 5.打印dp数组查看分析问题 LeetCode T62 不同路径 题目链接:62. 不同路径 - 力扣(LeetCode) 题目思路: 注:n行m列而不是m行n列 1.确定dp数组含义 代表到达此下标有多少条…...
【计算机网络】分层模型和应用协议
网络分层模型和应用协议 1. 分层模型 1.1 五层网络模型 网络要解决的问题是:两个程序之间如何交换数据。 四层?五层?七层? 2. 应用层协议 2.1 URL URL(uniform resource locator,统一资源定位符&#…...
Python框架之Flask入门和视图
一、Flask入门和视图 需要安装Pycharm专业版 1. Flask简介 Python后端的2个主流框架 Flask 轻量级框架Django 重型框架 Flask是一个基于Python实现的web开发微框架 官方文档:https://flask.palletsprojects.com/ 中文文档:https://dormousehole.readthe…...

streamWriter.WriteLine
streamWriter.WriteLine写入文件有回车行 using (System.IO.StreamWriter streamWriter new System.IO.StreamWriter("D:\123.txt", false, System.Text.Encoding.Default)) { streamWriter.Write(str.Replace("…...

一键添加色彩变幻效果,视频剪辑从未如此简单!
在视频制作过程中,给视频添加特效是必不可少的环节。而其中,色彩变幻效果作为一种常用的特效,能够为视频增添独特的氛围和视觉冲击力。然而,对于许多初学者来说,如何批量给视频添加色彩变幻效果特效功能却是一个难题。…...
Linux的简介和环境搭建
简介 Linux是一套免费使用和自由传播的类Unix操作系统,是一个基于POSIX和Unix的多用户、多任务、支持多线程和多CPU的操作系统。它能运行主要的Unix工具软件、应用程序和网络协议。它支持32位和64位硬件。Linux继承了Unix以网络为核心的设计思想,是一个…...

你看现在的程序员,是怎么解bug的
大家好,我是伍六七。 干程序员的都会碰到各种各样的 bug,有的 bug 我们看一眼、或者多看几眼就能看出来问题。 但是,也有很多问题,我们看不出来,这个时候,我们不妨把我们的代码扔给 GPT,看看它…...

CSS3背景样式
在CSS 2.1中,background属性的功能还无法满足设计的需求,为了方便设计师更灵活地设计需要的网页效果,CSS3在原有background基础上新增了一些功能属性,可以在同一个对象内叠加多个背景图像,可以改变背景图像的大小尺寸&…...

JAVA同城服务同城圈子真人躲猫猫系统的玩法流程
在现在科技的发展和互联网的普及,线上社交游戏在人们的生活中占据了越来越重要的地位。JAVA同城服务同城圈子真人躲猫猫系统就是一种结合了线上社交和线下实体位置服务的全新游戏模式。在这个游戏中,玩家们可以在同一城市中寻找隐藏的对手,体…...
C++继承——圆形和圆柱体
C继承 Circular圆形类 /*圆形类*/ class Circular { private:const static double PI;double R 0; public:Circular() default;Circular(double r);double GetArea(); /*圆面积*/double GetGirth(); /*圆周长*/ }; const double Circular::PI 3.14;Circular::Circula…...
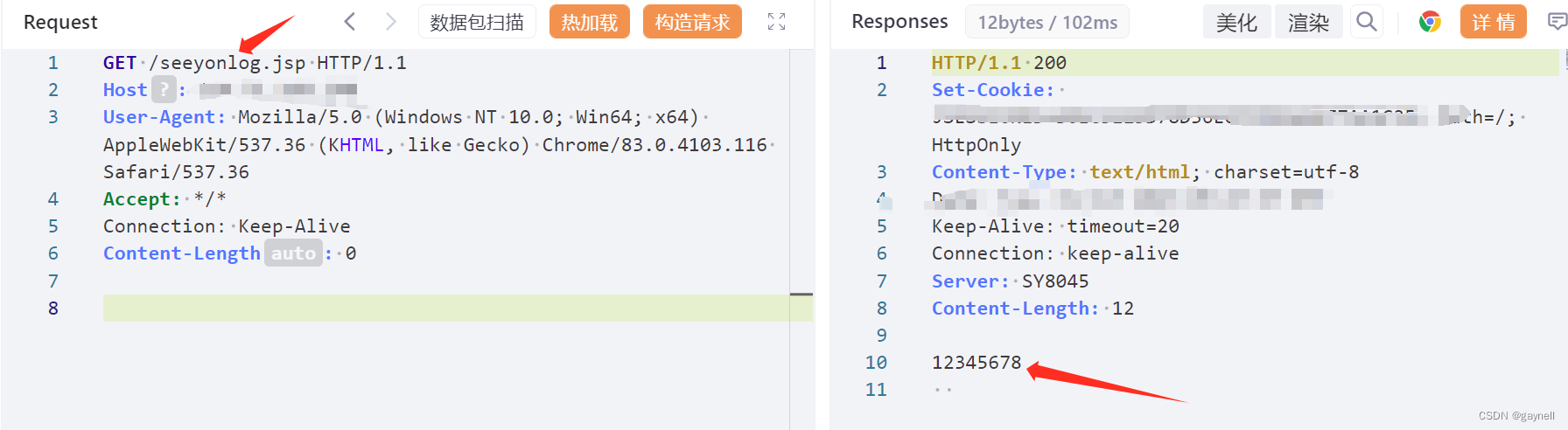
致远OA wpsAssistServlet任意文件上传漏洞复现 [附POC]
文章目录 致远OA wpsAssistServlet任意文件上传漏洞复现 [附POC]0x01 前言0x02 漏洞描述0x03 影响版本0x04 漏洞环境0x05 漏洞复现1.访问漏洞环境2.构造POC3.复现 0x06 修复建议 致远OA wpsAssistServlet任意文件上传漏洞复现 [附POC] 0x01 前言 免责声明:请勿利用…...
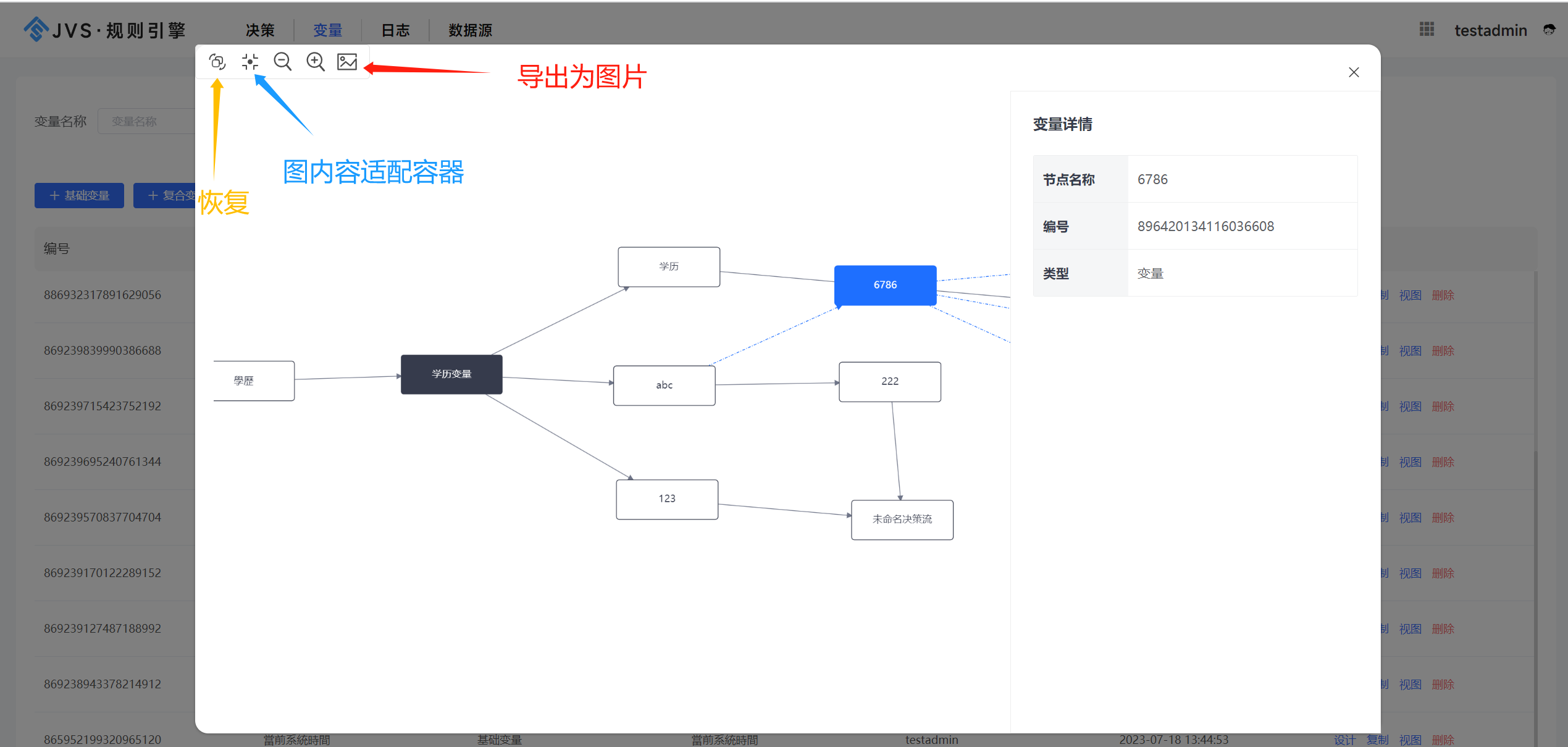
Java规则引擎2.1.8版本新增功能说明
规则引擎更新功能 新增: 1.决策结束节点新增结果导出excel功能; 在决策流程的结束节点,可以将决策结果导出为Excel文件。这个功能为用户提供了更多的灵活性和便利性,使他们能够轻松地将决策结果数据进行进一步的分析和处理。 2.新增公有变…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

rknn toolkit2搭建和推理
安装Miniconda Miniconda - Anaconda Miniconda 选择一个 新的 版本 ,不用和RKNN的python版本保持一致 使用 ./xxx.sh进行安装 下面配置一下载源 # 清华大学源(最常用) conda config --add channels https://mirrors.tuna.tsinghua.edu.cn…...

2025年- H71-Lc179--39.组合总和(回溯,组合)--Java版
1.题目描述 2.思路 当前的元素可以重复使用。 (1)确定回溯算法函数的参数和返回值(一般是void类型) (2)因为是用递归实现的,所以我们要确定终止条件 (3)单层搜索逻辑 二…...

Linux-进程间的通信
1、IPC: Inter Process Communication(进程间通信): 由于每个进程在操作系统中有独立的地址空间,它们不能像线程那样直接访问彼此的内存,所以必须通过某种方式进行通信。 常见的 IPC 方式包括&#…...

拟合问题处理
在机器学习中,核心任务通常围绕模型训练和性能提升展开,但你提到的 “优化训练数据解决过拟合” 和 “提升泛化性能解决欠拟合” 需要结合更准确的概念进行梳理。以下是对机器学习核心任务的系统复习和修正: 一、机器学习的核心任务框架 机…...
