数据结构第一课-----------数据结构的介绍

作者前言

🎂 ✨✨✨✨✨✨🍧🍧🍧🍧🍧🍧🍧🎂
​🎂 作者介绍： 🎂🎂
🎂 🎉🎉🎉🎉🎉🎉🎉 🎂
🎂作者id：老秦包你会， 🎂
简单介绍：🎂🎂🎂🎂🎂🎂🎂🎂🎂🎂🎂🎂🎂🎂🎂
喜欢学习C语言和python等编程语言，是一位爱分享的博主，有兴趣的小可爱可以来互讨 🎂🎂🎂🎂🎂🎂🎂🎂
🎂个人主页::小小页面🎂
🎂gitee页面:秦大大🎂
🎂🎂🎂🎂🎂🎂🎂🎂
🎂 一个爱分享的小博主 欢迎小可爱们前来借鉴🎂

---

介绍

数据结构：是计算机存储、组织数据的方式，指的是相互之间存在一种或者多种特定关系的数据元素的集合
如果学习过数据库的大佬就会知道，数据库主要是在硬盘上操作的管理数据，一般归结为增删改查，里面的精髓全部容纳在里面，而数据结构是在内存上管理数据的，

内存的读取速度快，价格高，带电存储，一旦掉电就会数据丢失，而硬盘的读取和存储速度就很慢，价格低 ，不带电存储，掉电不会数据丢失。

算法是定义良好的计算过程，他取一个或者一组的值输入，并产生出一个或者一组值作为输出，简单的说就是输入数据到输出数据之间的过程就是算法

算法的时间复杂度和空间复杂度

算法效率

1.代码简洁不一定效率高

#include<stdio.h>
int Fib(int a)
{if (a < 3){return 1;}else{return Fib(a - 1) + Fib(a - 2);}
}
int main()
{printf("%d", Fib(2));return 0;

这道题主要是求斐波那契数，使用了递归，代码虽然简便，但是计算过程却不简便，

衡量一个算法的好坏主要从两个维度来衡量。一个是时间复杂度，一个是空间复杂度，
时间复杂度主要是用来衡量一个算法的时间，时间越短，空间复杂度就越好。
空间复杂度是用来衡量一个算法在计算过程中空间的使用情况，可以理解，这个算法在使用过程中创建了多少个变量、数组、结构，浪费了多少内存，

时间复杂度

时间复杂度的定义：在计算机科学中，算法的时间复杂度是一个函数，它定量描述了该算法的运行时间，一个算法执行所消耗的时间，一个算法所花费的时间和其中语句的执行次数成正比，算法中的基本操作的执行次数就为算法的时间复杂度
注意这个函数不是C语言里面的函数，而是我们的数学函数，例如
aX^2 + bX+ c ; 这样的表达式
我们来练习一下

void Func1(int N)
{
int count = 0;for (int i = 0; i < N ; ++ i)
{for (int j = 0; j < N ; ++ j){++count;}
}for (int k = 0; k < 2 * N ; ++ k)
{++count;
}
int M = 10;
while (M--)
{++count;
}

我们可以利用我们学习的C语言常识来理解一下,第一个for循环执行了NN次
在外层的for首先每循环一次,里面for就会循环N次,外层有N次,总共就会循环NN次,第二个for循环了2N次
第三个while循环了10次
int count = 0;也执行了一次
所以全部就执行了 F(N) = NN+ 2N+ 11，随着N的增大主要影响这个表达式的结果时NN，所以我们计算时间复杂度就要取这个影响最大的项，那我们就可以使用一种方法大O渐进表示法
O(N^2)

大O渐进表示法

主要是进行估算的
大O符号（Big O notation）：是用于描述函数渐进行为的数学符号。
推导大O阶方法：
1、用常数1取代运行时间中的所有加法常数。例如O(1),只要运行的次数是常数就用这个来表示
2、在修改后的运行次数函数中，只保留最高阶项。
3、如果最高阶项存在且不是1，则去除与这个项目相乘的常数。得到的结果就是大O阶。

时间复杂度练习

void Func2(int N)
{int count = 0;for (int k = 0; k < 2 * N ; ++ k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}

这里我们可以的数学表达是就是 F(N） = 2*N + 10, 大O渐进表示就是O(N)

// 计算Func3的时间复杂度？
void Func3(int N, int M)
{int count = 0;for (int k = 0; k < M; ++ k){++count;}for (int k = 0; k < N ; ++ k){++count;}printf("%d\n", count);
}

这道题的时间复杂度的数学表达式是M+ N+ 1,大O渐进表示O(M + N),
这里如果是M大于N就是O(M),如果是M小于 N就是O(N),如果M=N就是O(M)或者O(N)

void Func4(int N)
{int count = 0;for (int k = 0; k < 100; ++ k){++count;}printf("%d\n", count);
}

这里的时间复杂度是一个常量,是常量,大O渐进表示就是O(1).

下面我引入一个函数

#include<stdio.h>
#include<string.h>
int main()
{char *p = strchr("dfksdfsfkl", 's');printf("%p", p);return 0;
}

这个函数的作用是在一个字符串中找字符,找到就返回第一次出现的地址,否则返回NULL
str是要进行查找的字符串。
charcter是要查找的字符，它以整数形式传递，通常使用字符的ASCII码。
假设我们要找一个字符,这个字符可能存在第一个,可能中间,或者末尾,

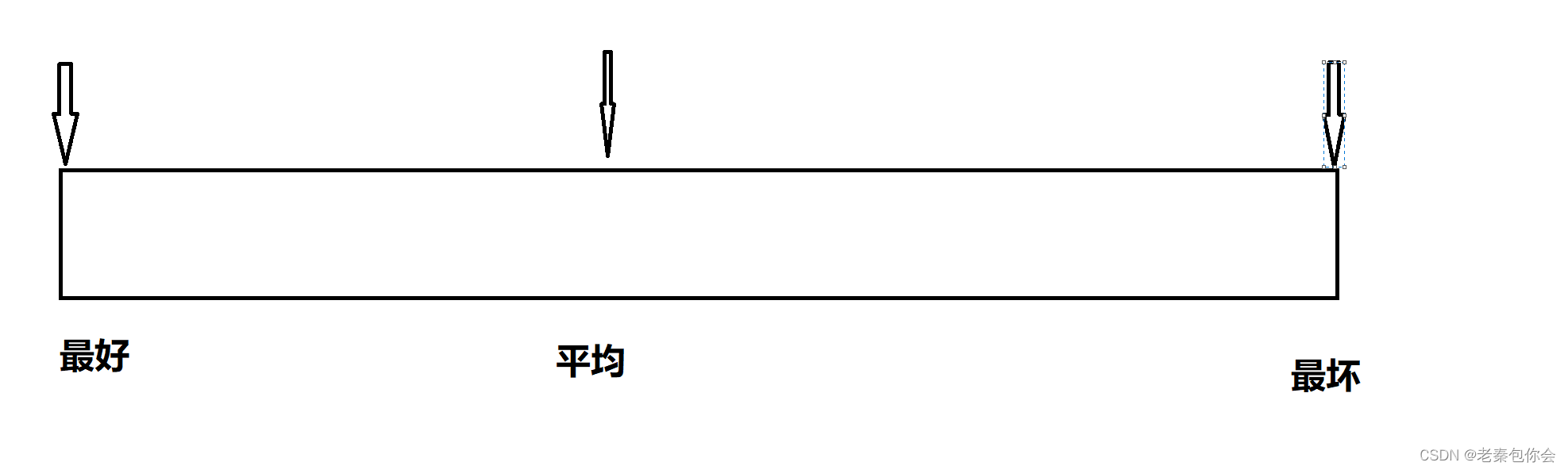
这种方法叫预期管理法
有些算法的时间复杂度存在最好、平均和最坏情况：
最坏情况：任意输入规模的最大运行次数(上界)
平均情况：任意输入规模的期望运行次数
最好情况：任意输入规模的最小运行次数(下界)
例如：在一个长度为N数组中搜索一个数据x
最好情况：1次找到
最坏情况：N次找到
平均情况：N/2次找到
在实际中一般情况关注的是算法的最坏运行情况，所以数组中搜索数据时间复杂度为O(N)

// 计算BubbleSort的时间复杂度？
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i-1] > a[i]){Swap(&a[i-1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}

这里的我们还要区分一下,两层for不一定是O(N^2),还有可能是O(N),这里的计算主要是次数
(n - 1) + (n - 2)+…+1 +0利用等差数列公式可以求出是n(n -1)/2
时间复杂度主要还是根据代码的思路去进行判断,而不是根据代码,前面根据代码计算时间复杂度是因为前面的代码思路简单

int BinarySearch(int* a, int n, int x)
{assert(a);int begin = 0;int end = n-1;// [begin, end]：begin和end是左闭右闭区间，因此有=号while (begin <= end){int mid = begin + ((end-begin)>>1);if (a[mid] < x)begin = mid+1;else if (a[mid] > x)end = mid-1;elsereturn mid;}return -1;
}

这里是二分查找,使用二分查找的的前提是要有序,无序就不行
时间复杂度是O(log N),为啥是O(log N),我们可以想象一下,当我们通过二分查找当找到最后一个的时候,我们可以反过来想,每次寻找元素个数都减半,那我们通过最后一个元素来反推出元素总数
假设最后找到最后一个元素, 次数设为x ,总数是N , 122*…2 = N我们可以发现,当我们每找一次就会除2.那有找了x次就会有x个2,也就是2^x = N,时间复杂度算的是次数,x = log N(默认以2为底)

// 计算阶乘递归Fac的时间复杂度？
long long Fac(size_t N)
{if(0 == N)return 1;return Fac(N-1)*N;
}

这里的时间复杂度为O(N), 当参数值为N时 函数调用N次,每次为1,所以时间复杂度就是O(N),时间复杂度算的是次数

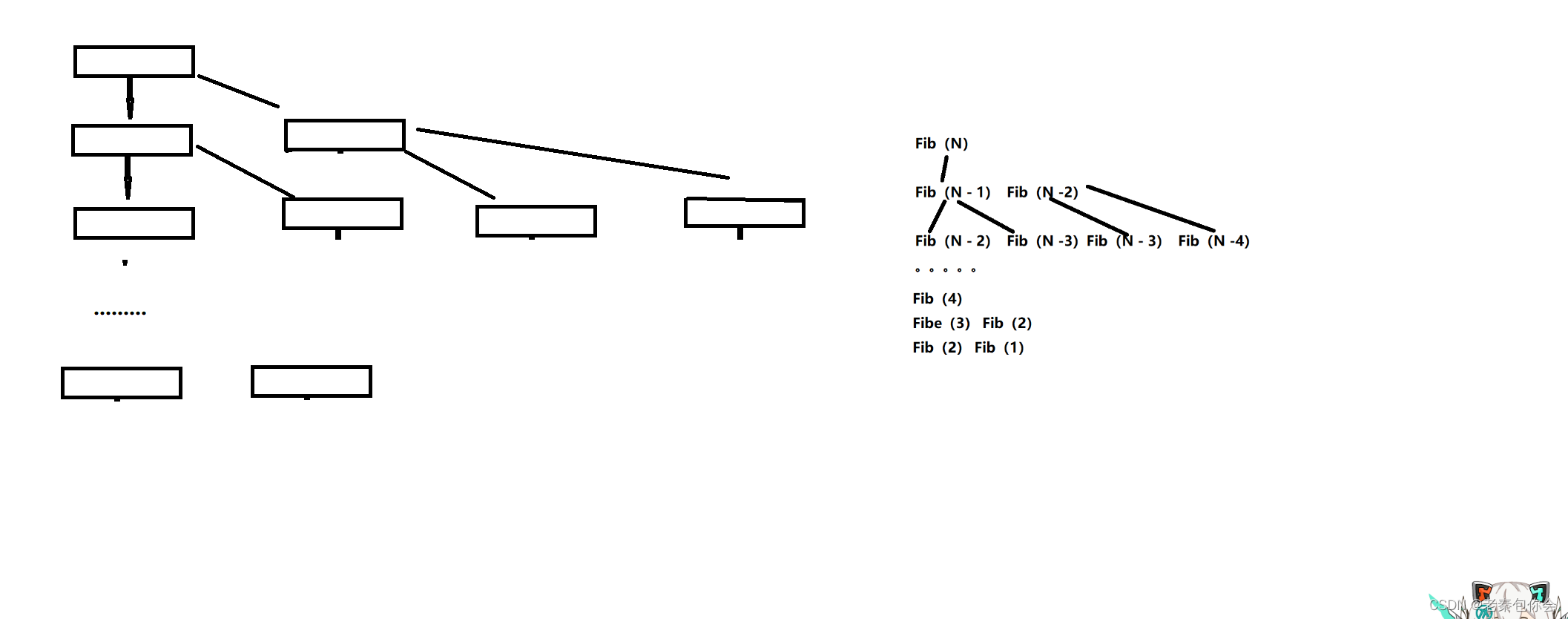
// 计算斐波那契递归Fib的时间复杂度？
long long Fib(size_t N)
{if(N < 3)return 1;return Fib(N-1) + Fib(N-2);
}

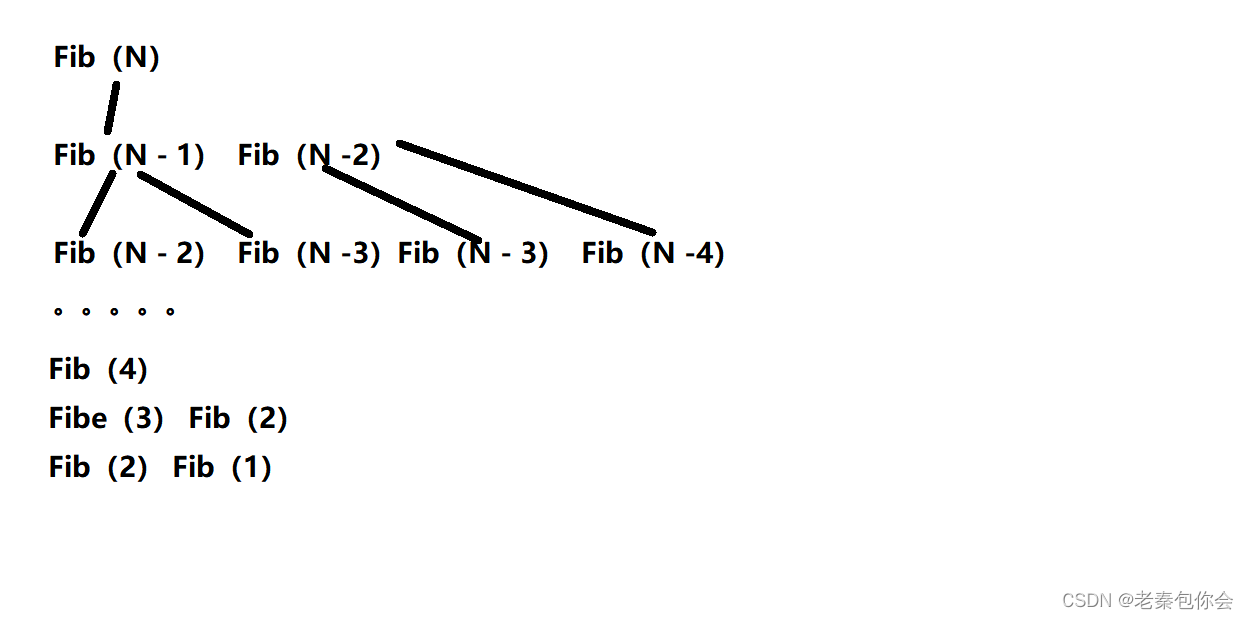
我们可以看左边,就像一个直角三角型一样 , 总共有N层 ,每一层是2的幂
第一层 2^0,第二层2 ^1 …,
最终的结果 2^0 + 2^1 +2 ^2 +2 ^3 +…+ 2^(N -2),等比数列 :2^(N- 1) - 1
所以最终是O(2 ^N)，这种思路我们可以学习，但是实际价值却很低
我们可以使用循环来减少时间复杂度

#include<stdio.h>
#include<string.h>
int main()
{int n1 = 1;int n2 = 1;int n3 = 1;int num = 0;scanf("%d", &num);int i = 0;for (i = 0; i < (num - 2) && num >2; i++){n3 = n1 + n2;n1 = n2;n2 = n3;}printf("%d", n3);return 0;
}

​

空间复杂度

空间复杂度也是一个数学表达式，是对一个算法在运行过程中临时占用存储空间大小的量度 。
空间复杂度不是程序占用了多少bytes的空间，因为这个也没太大意义，所以空间复杂度算的是变量的个数。
空间复杂度计算规则基本跟实践复杂度类似，也使用大O渐进表示法。
注意：函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了，因此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定。

// 计算BubbleSort的空间复杂度？
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i-1] > a[i]){Swap(&a[i-1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}

这里的变量创建了3个空间复杂度s
在计算空间复杂度时，形参通常不会被考虑在内。空间复杂度主要关注的是算法执行过程中所使用的额外空间，而形参通常是在函数调用时传递的参数，不会占用额外空间。因此，在计算空间复杂度时，通常只考虑算法中使用的变量、数据结构和临时空间等。

// 计算Fibonacci的空间复杂度？
// 返回斐波那契数列的前n项
long long* Fibonacci(size_t n)
{if(n==0)return NULL;long long * fibArray = (long long *)malloc((n+1) * sizeof(long long));fibArray[0] = 0;fibArray[1] = 1;for (int i = 2; i <= n ; ++i){fibArray[i] = fibArray[i - 1] + fibArray [i - 2];}return fibArray;
}

这里主要是创建了n+1个空间进行存储，空间复杂度是O(n)

那下面我来推荐一道题

这道题我们可以通过创建额外的空间让时间复杂度降低, 数组中的元素充当额外数组的下标,遍历一遍额外数组找出不存在的,就可以解出来,空间复杂度是O(n).时间复杂度是O(n)

// 计算阶乘递归Fac的空间复杂度？
long long Fac(size_t N)
{if(N == 0)return 1;return Fac(N-1)*N;
}

这里主要是递归，函数里面调用函数
调用情况：

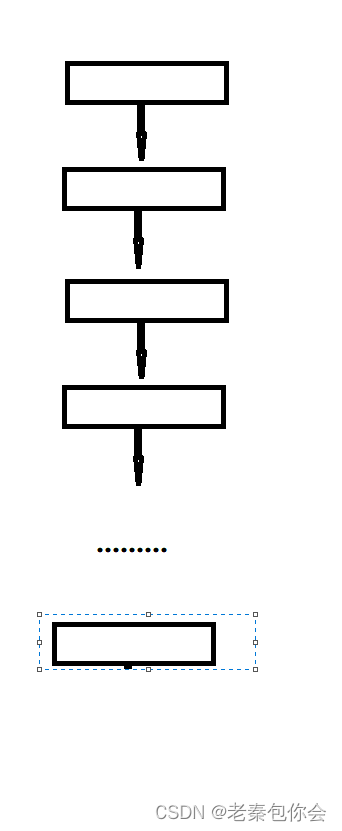
一共调用了N次，总共创建了N个空间，空间复杂度是O（N）
而我们计算斐波那契数的空间复杂度也是O(N)

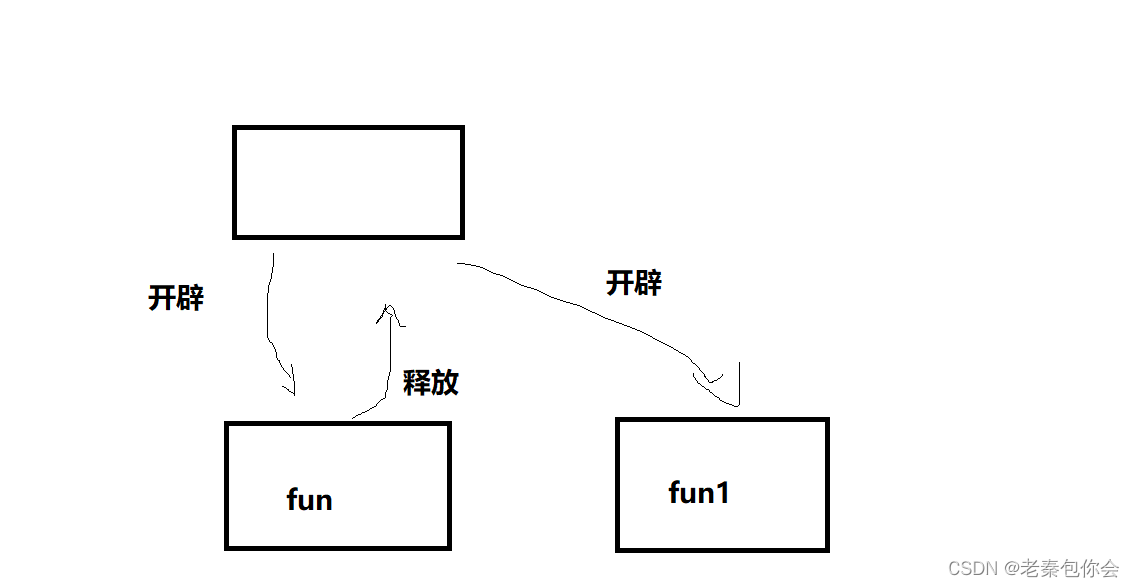
因为递归的空间复杂度,也是空间的累计,但是不同的是空间是重复利用,为啥要这样说呢?
因为函数调用是一个个调用的,不是一下子调用全部函数
下面的代码可以演示

#include<stdio.h>
#include<string.h>
int fun(int N)
{int a = 0;printf("%p\n", &a);
}
int fun1(int N)
{int a = 0;printf("%p\n", &a);
}
int main()
{fun(1);fun1(1);return 0;
}

总结

时间复杂度和空间复杂度就介绍到这里了,感兴趣的小可爱可以私聊我