pt权重转onnx记录
方法:
1.一般YOLO 会自带一个权重pt转onnx模型的代码
export.py
2.打开export.py ,我们运行该文件可以通过命令行运行,对照修改argument参数即可
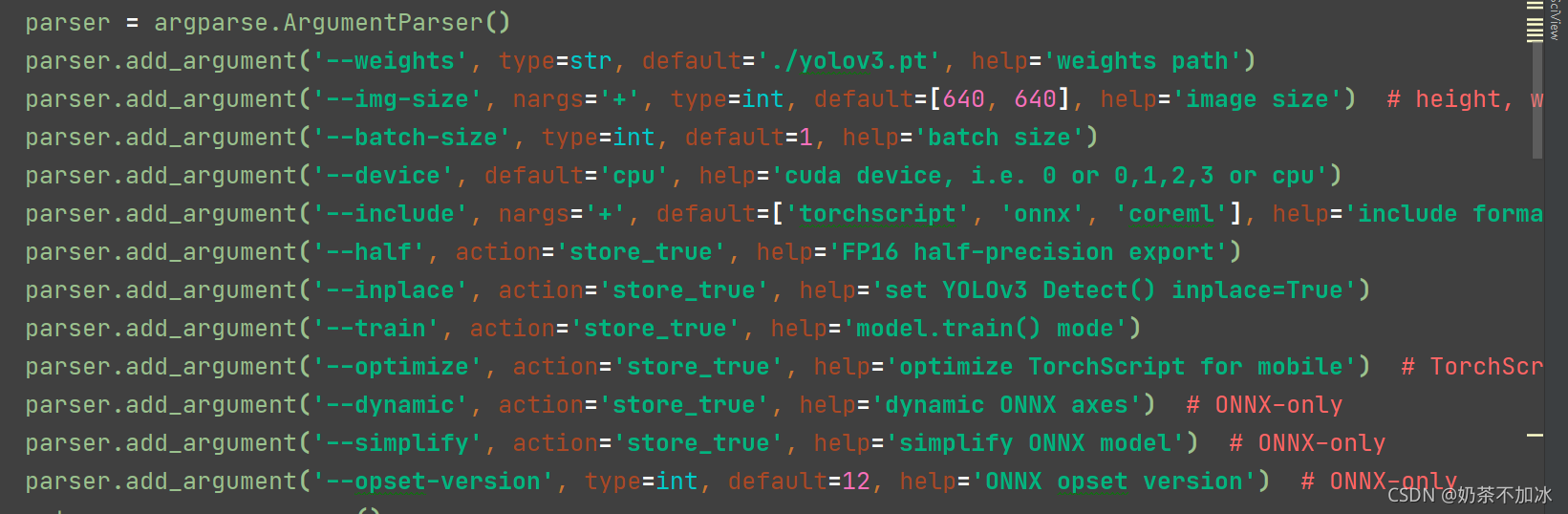
3.运行命令行如下:
python ./models/export.py --weights ./models/best.ptweights:指你训练好的权重文件,看你放在哪个文件夹中。
4.导出的onnx文件就会在你best.pt的相同目录当中,你不修改–include参数的话,一般会出现三个文件,分别是torchscript, onnx, coreml。一般onnx和torchscript文件大小为你的pt文件的两倍大小,如果不是2倍大小,那可能就是转错了。
注意:不要进入models文件夹中运行export.py,要不然会报错误,找不到model
转自:
pt权重文件转onnx详解(记录)_pt转onnx-CSDN博客文章浏览阅读1.3w次,点赞9次,收藏58次。pt权重转onnx记录方法1.一般YOLOv3和YOLOv5 会自带一个权重pt转onnx模型的代码export.pyexport.py在models文件夹中2.打开export.py ,我们运行该文件可以通过命令行运行,对照修改argument参数即可3.运行命令行如下:python ./models/export.py --weights ./models/best.pt --batch-size 16weights:指你训练好的权重文件,看你放在哪个文件夹中。batch-_pt转onnxhttps://blog.csdn.net/weixin_44312422/article/details/121510796
相关文章:
pt权重转onnx记录
方法: 1.一般YOLO 会自带一个权重pt转onnx模型的代码 export.py 2.打开export.py ,我们运行该文件可以通过命令行运行,对照修改argument参数即可 3.运行命令行如下: python ./models/export.py --weights ./models/best.pt weights&#x…...

瑞数专题五
今日文案:焦虑,想象力过度发酵的产物。 网址:https://www.iyiou.com/ 专题五主要是分享瑞数6代。6代很少见,所以找理想哥要的,感谢感谢。 关于瑞数作者之前已经分享过4篇文章,全都收录在瑞数专栏中了&am…...

【Androidstudio学习笔记】设计引导页功能
设计引导页功能 主目录功能描述大致思路准备工作代码ActivityAdapter滑动动画 总结 主目录 功能描述 此功能用于新用户第一次进入应用时在部分较为复杂的功能使用前展示的操作流程,当然也可以在后续的其他功能键重新查看引导流程 展示指定数量的引导页࿰…...
)
【python】中位数(暴力+最大最小堆)
题目: """ 对给定长度为N的非负整数序列A,计算前奇数项的中位数。 输入:首行表示序列长度N。次行为N个正整数A1至AN。 输出:输出共(N1)/2行(向下取整),第i行表示到第A1...2i-1项…...
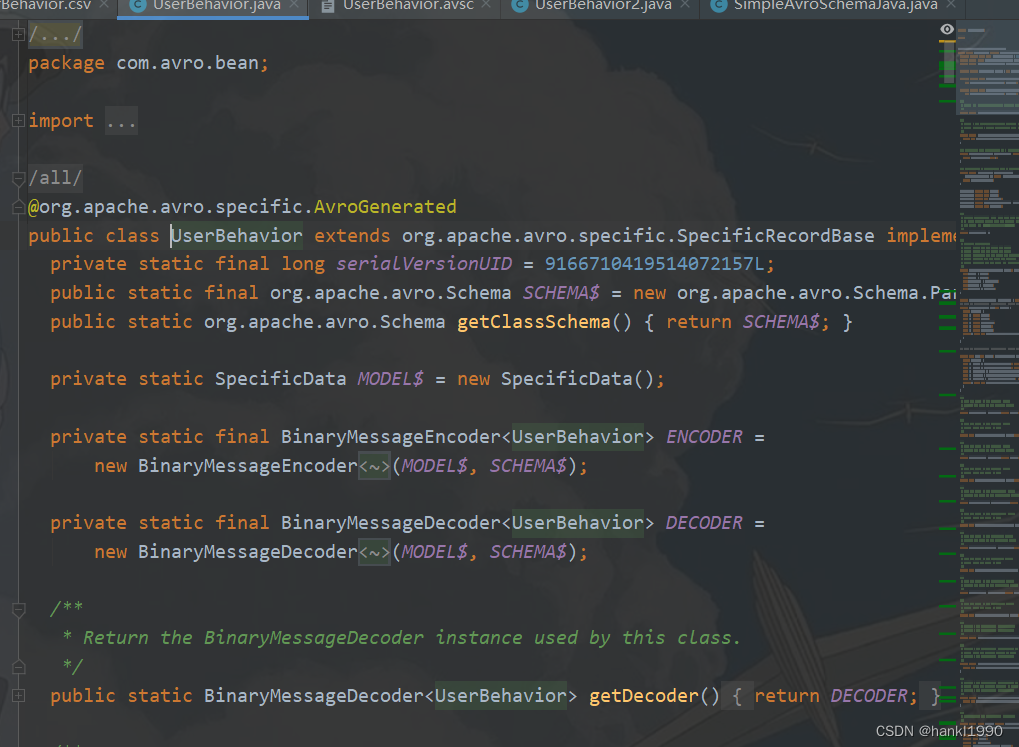
Avro 如何生成java Bean
作为一种很犀利的序列化的格式,avro在大数据量传输的时候很有优势。记录下。 1: .avsc 文件 {"namespace": "com.avro.bean","type": "record","name": "UserBehavior3","fields&qu…...

EG4003-一颗为微波、红外信号放大及处理输出的数模混合芯片
产品描述: EG4003是一款特意为微波、红外信号放大及处理输出的数模混合芯片,内部集成了运算放大器、双门限电压比较器、参考电压源、延时时间定时器和封锁时间定时器及状态控制器等,专用于防盗报警系统、人体门控制装置、照明控制开关等场合。…...

kafka生产者源码精华总结
kafka的源码阅读起来思路很清晰,命名也很规范。 KafkaProducer值得学习的地方: Kafka的网络部分的设计绝对是一个亮点,Kafka基于NIO封装了一套自己的网络架构,支持一个客户端与多个Broker建立连接。处理拆包和粘包的思路和代码&…...

边界缩小维护最值——倒序枚举/中部切开:1101T2
http://cplusoj.com/d/senior/p/CPNOIPB 发现维护边界缩小类最值很难做,有两种常见方法: 倒序进行,边界就变成扩大了在 m i d mid mid 处切开,复杂度可以均摊...

vue实现购物车案例
要求 可以进行购物车水果删除可以进行水果数量增减可以进行总价计算、购物车商品计算选中所有水果也会一同勾选全选框,全选框勾选也能选中所有水果可以记录购物车状态,当页面关闭后重新打开可以看到原先的购物车数据 功能代码 <!DOCTYPE html>…...

工业4G路由器桥接多网络,提升工业环境网络覆盖
一款专为工业环境应用所设计的物联网通讯设备“工业4G路由器”,它具有多种功能和特性。其中之一就是桥接功能,在工业领域中被广泛应用并起着重要的通信作用。 桥接功能是指工业4G路由器通过无线网络的方式,为不同的工业设备提供网络并将其连…...

docker 存储目录迁移
参考:【Docker专题】WSL镜像包盘符迁移详细笔记 - 掘金 docker迁移 一 默认目录 Windows版本(Windows 10 wsl 2)docker 默认程序安装到c盘,数据存放于 C:\Users\当前用户名\AppData\Local\Docker\wsl\data\ext4.vhdx 这样会导致…...
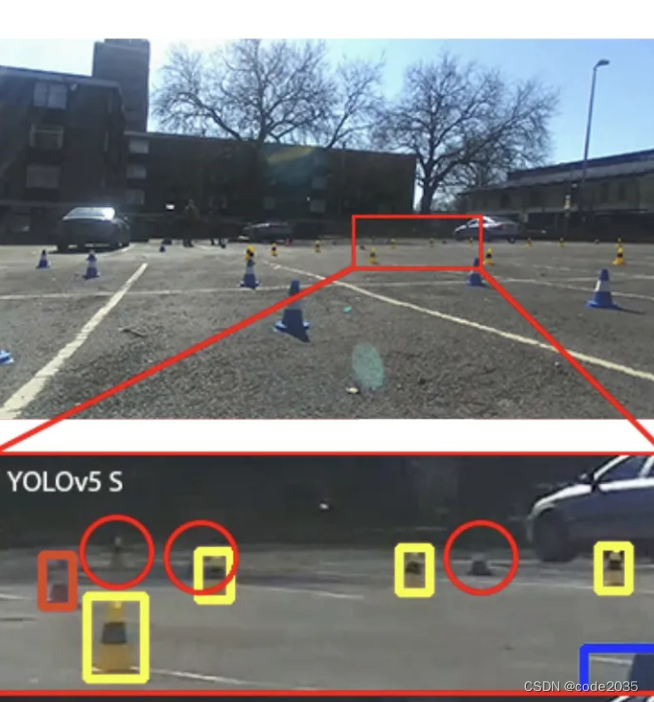
Yolo-Z:改进的YOLOv5用于小目标检测
目录 一、前言 二、背景 三、新思路 四、实验分析 论文地址:2112.11798.pdf (arxiv.org) 一、前言 随着自动驾驶汽车和自动驾驶赛车越来越受欢迎,对更快、更准确的检测器的需求也在增加。 虽然我们的肉眼几乎可以立即提取上下文信息,即…...

系列八、Spring IOC有哪些扩展点,在什么时候调用
一、概述 Spring IOC的扩展点是指IOC在加载过程中,如何对即将要创建的bean进行扩展。 二、扩展点 2.1、实现BeanDefinitionRegistryPostProcessor 调用invokeBeanFactoryPostProcessors时,通过实现BeanDefinitionRegistryPostProcessor接口进行扩展。 …...

《AI时代架构师修炼之道:ChatGPT让架构师插上翅膀》
本专注于帮助架构师在AI时代 实现晋级、提高效率的图书 书中介绍了如何使用 ChatGPT 来完成架构设计的各个环节 并通过实战案例展示了ChatGPT在实际架构设计中的应用方法 关键点 1.架构设计新模式:让架构设计更高效、更快捷、更完美。 2.全流程解析:涵盖…...
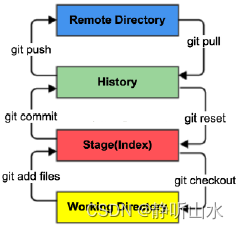
git命令清单
一、设置和配置 1.初始化一个新的仓库: git init2.克隆(Clone)一个远程仓库到本地: git clone <repository_url>3.配置用户信息: git config --global user.name "Your Name" git config --global…...

使用Nokogiri和OpenURI库进行HTTP爬虫
目录 一、Nokogiri库 二、OpenURI库 三、结合Nokogiri和OpenURI进行爬虫编程 四、高级爬虫编程 1、并发爬取 2、错误处理和异常处理 3、深度爬取 总结 在当今的数字化时代,网络爬虫已经成为收集和处理大量信息的重要工具。其中,Nokogiri和OpenUR…...
arcpy.message实现探索
arcpy 位置D:\Program Files\GeoScene\Pro\Resources\ArcPy\arcpy\__init__.py ”““AddMessage(消息) 创建可以使用任何GetMessages函数访问的地理处理信息消息(Severity0)。 message(字符串):要添加的消息。”“ arcpy.geoprocessing D:\Program Files\GeoScene\Pro\Re…...

centos卸载自带的Python3.6.8 安装指定的版本号
#卸载python3 rpm -qa|grep python3|xargs rpm -ev --allmatches --nodeps #删除所有残余文件 whereis python3 |xargs rm -frv#查看现有安装的python,验证是否删除干净 whereis python # 安装依赖 yum -y install zlib-devel bzip2-devel openssl-devel ncurses-de…...
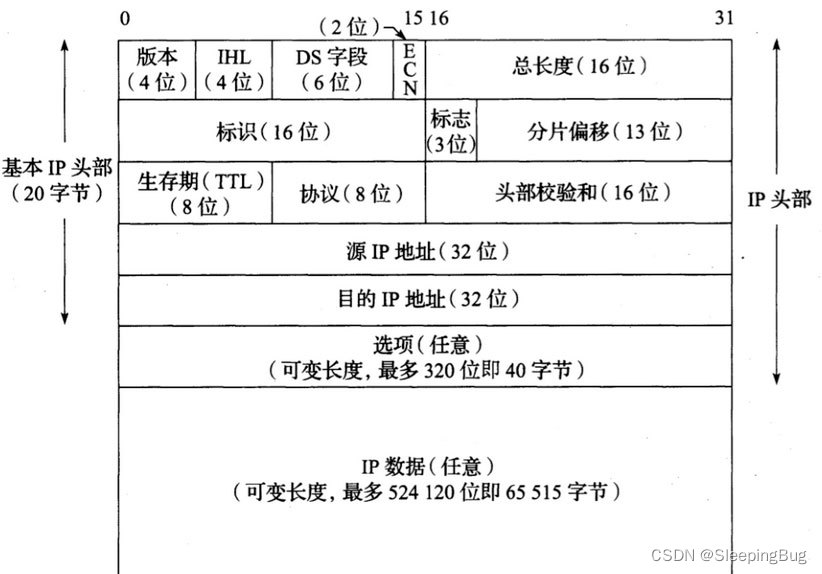
《TCP/IP详解 卷一:协议》第5章的IPv4数据报的IHL字段解释
首先说明一下,这里并不解释整个IPv4数据报各个字段的含义,仅仅针对IHL字段作解释。 我们先看下IPv4数据报格式 对于IHL字段, 《TCP/IP详解 卷一:协议》这么解释: IPv4数据报。头部大小可变,4位的IHL字段…...

想去银行的背完这些软件测试面试题,你就稳了...
前言 最近呢有很多的小伙伴问我有没有什么软件测试的面试题,由于我之前一直在忙工作上的事情,没有时间整理面试题,刚好最近休息了一下,顺便整理了一些面试题,现在就把整理的面试题分享给大家,废话就不多说…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...
