从零开始实现神经网络(一)_NN神经网络
参考文章:神经网络介绍
一、神经元
这一神经网络的基本单元,神经元接受输入,对它们进行一些数学运算,并产生一个输出。
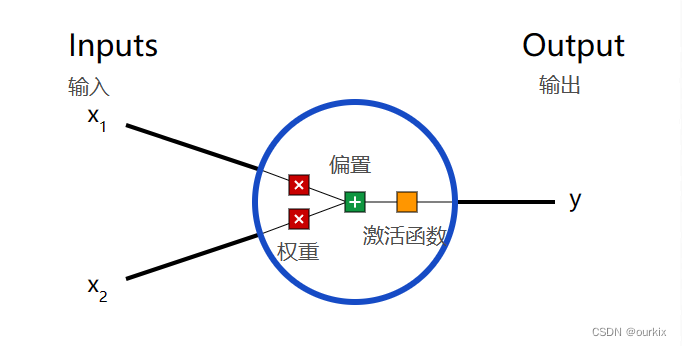
这里有三步。
首先,将每个输入(X1)乘以一个权重![]() :
:
接下来,将所有加权输入与偏置![]() 相加:
相加:
最后,总和通过激活函数![]() 传递:
传递:
激活函数
激活函数用于将无界输入转换为具有良好、可预测形式的输出。常用的激活函数是sigmoid功能:
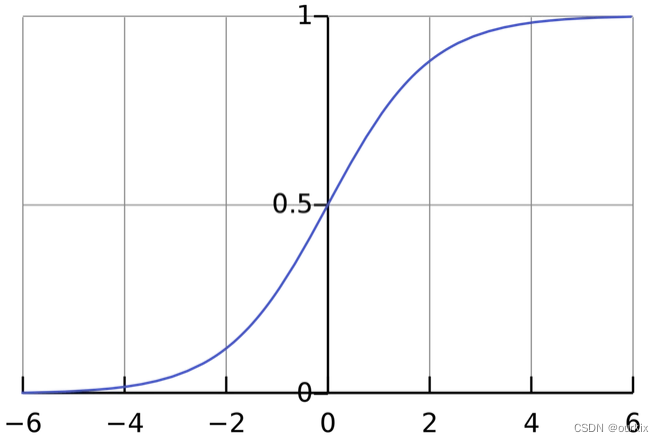
你可以把它想象成,压缩零到负无穷的数字到[-1,0],压缩0到正无穷的数字到[0,1]
举个例子:
这里写成向量形式,假设权重W = {w1,w2} = {0,1},输入X = {x1,x2} = {2,3},偏置b为1。
那么有一下计算:
下面来实现下代码:
import numpy as npdef sigmoid(x):# Our activation function: f(x) = 1 / (1 + e^(-x))return 1 / (1 + np.exp(-x))class Neuron:def __init__(self, weights, bias):self.weights = weightsself.bias = biasdef feedforward(self, inputs):# Weight inputs, add bias, then use the activation functiontotal = np.dot(self.weights, inputs) + self.biasreturn sigmoid(total)weights = np.array([0, 1]) # w1 = 0, w2 = 1
bias = 4 # b = 4
n = Neuron(weights, bias)x = np.array([2, 3]) # x1 = 2, x2 = 3
print(n.feedforward(x)) # 0.9990889488055994二. 将神经元组合成神经网络
神经网络只不过是一堆连接在一起的神经元。下面是一个简单的神经网络的样子:
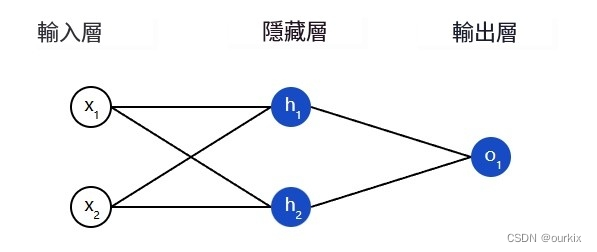
该网络有 2 个输入(x1和x2),一个带有 2 个神经元的隐藏层 (ℎ1和ℎ2),以及具有 1 个神经元 (o1).请注意,输入o1是来自ℎ1和h2- 这就是使它成为一个网络的原因。
隐藏层是输入(第一层)和输出(最后一层)之间的任何层。可以有多个隐藏层!
示例:前馈
让我们使用上图的网络,并假设所有神经元具有相同的权重w=[0,1],相同的偏差b=0,以及相同的 S 形激活函数。让h1,h2,o1表示它们所代表的神经元的输出。
如果我们传入输入会发生什么x=[2,3]?
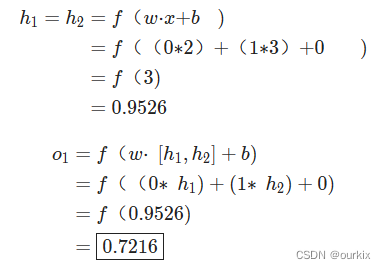
用于输入的神经网络的输出x=[2,3]是0.7216很简单,对吧?
神经网络可以有任意数量的层,这些层中可以有任意数量的神经元。基本思想保持不变:通过网络中的神经元向前馈送输入,以在最后获得输出。为简单起见,在本文的其余部分,我们将继续使用上图的网络。
神经网络的代码实现:
import numpy as np# ... code from previous section hereclass OurNeuralNetwork:'''A neural network with:- 2 inputs- a hidden layer with 2 neurons (h1, h2)- an output layer with 1 neuron (o1)Each neuron has the same weights and bias:- w = [0, 1]- b = 0'''def __init__(self):weights = np.array([0, 1])bias = 0# The Neuron class here is from the previous sectionself.h1 = Neuron(weights, bias)self.h2 = Neuron(weights, bias)self.o1 = Neuron(weights, bias)def feedforward(self, x):out_h1 = self.h1.feedforward(x)out_h2 = self.h2.feedforward(x)# The inputs for o1 are the outputs from h1 and h2out_o1 = self.o1.feedforward(np.array([out_h1, out_h2]))return out_o1network = OurNeuralNetwork()
x = np.array([2, 3])
print(network.feedforward(x)) # 0.7216325609518421三. 训练神经网络,第 1 部分
假设我们有以下测量值:
| 名字 | 重量(磅) | 高度(英寸) | 性 |
|---|---|---|---|
| 爱丽丝 | 133 | 65 | F |
| 鲍勃 | 160 | 72 | M |
| 查理 | 152 | 70 | M |
| 黛安娜 | 120 | 60 | F |
让我们训练我们的网络,根据某人的体重和身高预测他们的性别:
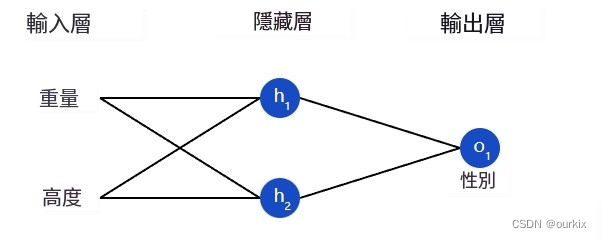
我们将用0代表男性,1代表女性,我们还将处理数据以使其更易于使用:
| 名字 | 重量(减去 135) | 高度(减去 66) | 性 |
|---|---|---|---|
| 爱丽丝 | -2 | -1 | 1 |
| 鲍勃 | 25 | 6 | 0 |
| 查理 | 17 | 4 | 0 |
| 黛安娜 | -15 | -6 | 1 |
我随意选择了减去的数值(135和66) 以使数值看起来更好。通常,会按平均值移动。
损失
在我们训练网络之前,我们首先需要一种方法来量化它做得有多“好”,以便它可以尝试做得“更好”。这就是损失所在。
我们将使用均方误差 (MSE) 损失:
让我们分解一下:
- n是样本数,即4(爱丽丝,鲍勃,查理,戴安娜)。
- y表示要预测的变量,即性别。
- yTrue是变量的真实值(“正确答案”)。例如yTRue因为爱丽丝的性别为1(女)。
- yPred是变量的预测值。这是我们的网络输出的任何内容。
称为平方误差。我们的损失函数只是取所有平方误差的平均值(因此得名均方误差)。我们的预测越好,我们的损失就越低!
更好的预测=更低的损失。
训练网络=试图将其损失降至最低。
损失计算示例
假设我们的网络总是输出0换句话说,它相信所有人类都是男性🤔。我们的损失会是什么?
| 名字 | yTRue | yPRED | |
|---|---|---|---|
| 爱丽丝 | 1 | 0 | 1 |
| 鲍勃 | 0 | 0 | 0 |
| 查理 | 0 | 0 | 0 |
| 黛安娜 | 1 | 0 | 1 |
均方误差的代码实现:
import numpy as npdef mse_loss(y_true, y_pred):# y_true and y_pred are numpy arrays of the same length.return ((y_true - y_pred) ** 2).mean()y_true = np.array([1, 0, 0, 1])
y_pred = np.array([0, 0, 0, 0])print(mse_loss(y_true, y_pred)) # 0.5四. 训练神经网络,第 2 部分
反向传播
我们现在有一个明确的目标:尽量减少神经网络的损失。我们知道我们可以改变网络的权重和偏差来影响其预测,但是我们如何以减少损失的方式做到这一点呢?
为简单起见,让我们假设我们的数据集中只有 爱丽丝:
| 名字 | 重量(减去 135) | 高度(减去66) | 性 |
|---|---|---|---|
| 爱丽丝 | -2 | -1 | 1 |
那么只是爱丽丝的均方误差损失(最后会带入yTrue的值进去):
另一种考虑损失的方法是作为权重和偏差的函数。让我们标记网络中的每个权重和偏差:

然后,我们可以将损失写为多变量函数:
L(w1,w2,w3,w4,w5,w6,b1,b2,b3)
想象一下,我们想调整w1.损失将如何L如果我们改变了,就改变w1?
这是一个偏导数的问题 可以回答。我们如何计算它?
首先,让我们根据以下方法(链式法则)重写偏导数:
这里我们可以求得,由于前面的MSE均方误差计算的就是神经网络的误差,MSE作为损失函数,所以有等式:
所以可以得出:
这里使用符合函数求导法则(对于函数的x进行求导,将得到
):
然后我们再搞清楚,由于yPred是预测值,而预测值由激活函数输出,所以能够得到等式:
由于改变w1只对h1有影响,所以可以写成: 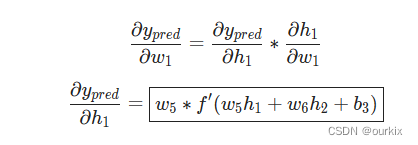
我们再对h1做同样的步骤(h1是上一层的激活函数),,同样是复合函数求导法则:

对于激活函数sigmoid的倒数:
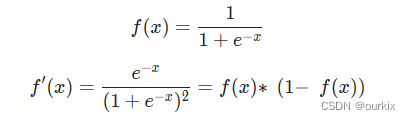
最终整合起来:
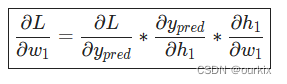
这种通过逆向计算偏导数的系统称为反向传播。
推导当前神经网络反向传播所用到的所有偏导公式:
例子:
我们将继续假设数据集中只有 爱丽丝:
| 名字 | 重量(减去 135) | 高度(减去 66) | 性 |
|---|---|---|---|
| 爱丽丝 | -2 | -1 | 1 |
让我们将所有权重初始化为1以及所有偏置为0.如果我们通过网络进行前馈传递,我们会得到:

网络输出yPred=0.524,这并不强烈支持男性 或女性 .让我们计算一下
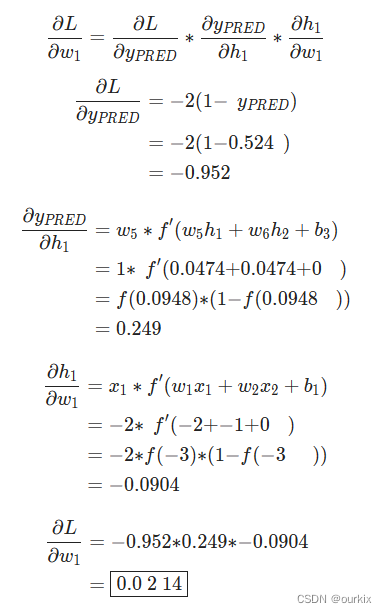
这里用到了上面所求得的sigmoid的倒数。
我们成功了!这告诉我们,由于所求的偏导结果为0.0214,是个正数,函数单调递增,所以
如果我们要增加w1(权重),L(损失)结果会增大一点点。
训练:随机梯度下降
我们现在拥有训练神经网络所需的所有工具!我们将使用一种称为随机梯度下降 (SGD) 的优化算法,该算法告诉我们如何改变权重和偏差以最小化损失。
就是这个方程式:
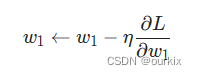
η是一个称为学习率的常数,它控制着我们训练的速度。我们所做的只是用旧权重减去学习率*偏导值:
- 如果
的值为正数,w1的减少,会使得L减少。
- 如果
的值为负数,w1的增加,会使得L减少。
如果我们对网络中的每个权重和偏差都这样做,损失将慢慢减少,我们的网络将得到改善。
我们的训练过程将如下所示:
- 从我们的数据集中选择一个样本。这就是它随机梯度下降的原因——我们一次只对一个样本进行操作。
- 计算所有损失相对于权重或偏差的偏导数(例如
,
等)。
- 使用更新公式更新每个权重和偏差。
- 返回步骤 1。
让我们看看它的实际效果吧!
代码:一个完整的神经网络
终于到了实现一个完整的神经网络的时候了:
| 名字 | 重量(减去 135) | 高度(减去 66) | 性 |
|---|---|---|---|
| 爱丽丝 | -2 | -1 | 1 |
| 鲍勃 | 25 | 6 | 0 |
| 查理 | 17 | 4 | 0 |
| 黛安娜 | -15 | -6 | 1 |
import numpy as npdef sigmoid(x):# Sigmoid activation function: f(x) = 1 / (1 + e^(-x))return 1 / (1 + np.exp(-x))def deriv_sigmoid(x):# Derivative of sigmoid: f'(x) = f(x) * (1 - f(x))fx = sigmoid(x)return fx * (1 - fx)def mse_loss(y_true, y_pred):# y_true and y_pred are numpy arrays of the same length.return ((y_true - y_pred) ** 2).mean()class OurNeuralNetwork:'''A neural network with:- 2 inputs- a hidden layer with 2 neurons (h1, h2)- an output layer with 1 neuron (o1)*** DISCLAIMER ***:The code below is intended to be simple and educational, NOT optimal.Real neural net code looks nothing like this. DO NOT use this code.Instead, read/run it to understand how this specific network works.'''def __init__(self):# Weightsself.w1 = np.random.normal()self.w2 = np.random.normal()self.w3 = np.random.normal()self.w4 = np.random.normal()self.w5 = np.random.normal()self.w6 = np.random.normal()# Biasesself.b1 = np.random.normal()self.b2 = np.random.normal()self.b3 = np.random.normal()def feedforward(self, x):# x is a numpy array with 2 elements.h1 = sigmoid(self.w1 * x[0] + self.w2 * x[1] + self.b1)h2 = sigmoid(self.w3 * x[0] + self.w4 * x[1] + self.b2)o1 = sigmoid(self.w5 * h1 + self.w6 * h2 + self.b3)return o1def train(self, data, all_y_trues):'''- data is a (n x 2) numpy array, n = # of samples in the dataset.- all_y_trues is a numpy array with n elements.Elements in all_y_trues correspond to those in data.'''learn_rate = 0.1epochs = 1000 # number of times to loop through the entire datasetfor epoch in range(epochs):for x, y_true in zip(data, all_y_trues):# --- Do a feedforward (we'll need these values later)sum_h1 = self.w1 * x[0] + self.w2 * x[1] + self.b1h1 = sigmoid(sum_h1)sum_h2 = self.w3 * x[0] + self.w4 * x[1] + self.b2h2 = sigmoid(sum_h2)sum_o1 = self.w5 * h1 + self.w6 * h2 + self.b3o1 = sigmoid(sum_o1)y_pred = o1# --- Calculate partial derivatives.# --- Naming: d_L_d_w1 represents "partial L / partial w1"d_L_d_ypred = -2 * (y_true - y_pred)# Neuron o1d_ypred_d_w5 = h1 * deriv_sigmoid(sum_o1)d_ypred_d_w6 = h2 * deriv_sigmoid(sum_o1)d_ypred_d_b3 = deriv_sigmoid(sum_o1)d_ypred_d_h1 = self.w5 * deriv_sigmoid(sum_o1)d_ypred_d_h2 = self.w6 * deriv_sigmoid(sum_o1)# Neuron h1d_h1_d_w1 = x[0] * deriv_sigmoid(sum_h1)d_h1_d_w2 = x[1] * deriv_sigmoid(sum_h1)d_h1_d_b1 = deriv_sigmoid(sum_h1)# Neuron h2d_h2_d_w3 = x[0] * deriv_sigmoid(sum_h2)d_h2_d_w4 = x[1] * deriv_sigmoid(sum_h2)d_h2_d_b2 = deriv_sigmoid(sum_h2)# --- Update weights and biases# Neuron h1self.w1 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_w1self.w2 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_w2self.b1 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_b1# Neuron h2self.w3 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_w3self.w4 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_w4self.b2 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_b2# Neuron o1self.w5 -= learn_rate * d_L_d_ypred * d_ypred_d_w5self.w6 -= learn_rate * d_L_d_ypred * d_ypred_d_w6self.b3 -= learn_rate * d_L_d_ypred * d_ypred_d_b3# --- Calculate total loss at the end of each epochif epoch % 10 == 0:y_preds = np.apply_along_axis(self.feedforward, 1, data)loss = mse_loss(all_y_trues, y_preds)print("Epoch %d loss: %.3f" % (epoch, loss))# Define dataset
data = np.array([[-2, -1], # Alice[25, 6], # Bob[17, 4], # Charlie[-15, -6], # Diana
])
all_y_trues = np.array([1, # Alice0, # Bob0, # Charlie1, # Diana
])# Train our neural network!
network = OurNeuralNetwork()
network.train(data, all_y_trues)随着网络学习,我们的损失稳步减少: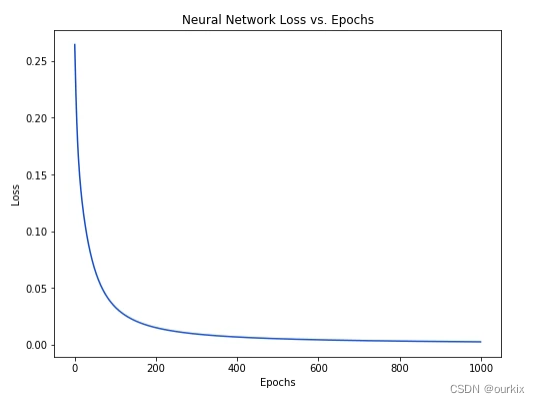
我们现在可以使用网络来预测性别:
# Make some predictions
emily = np.array([-7, -3]) # 128 pounds, 63 inches
frank = np.array([20, 2]) # 155 pounds, 68 inches
print("Emily: %.3f" % network.feedforward(emily)) # 0.951 - F
print("Frank: %.3f" % network.feedforward(frank)) # 0.039 - M相关文章:

从零开始实现神经网络(一)_NN神经网络
参考文章:神经网络介绍 一、神经元 这一神经网络的基本单元,神经元接受输入,对它们进行一些数学运算,并产生一个输出。 这里有三步。 首先,将每个输入(X1)乘以一个权重: 接下来&…...

C语言 每日一题 Day10
1.使用函数判断完全平方数 本题要求实现一个判断整数是否为完全平方数的简单函数。 函数接口定义: int IsSquare(int n); 其中n是用户传入的参数,在长整型范围内。如果n是完全平方数,则函数IsSquare必须返回1,否则返回0。 代码实…...
C++继承——矩形和长方体
Rectangle矩形类 /*矩形类*/ class Rectangle { private:double L 0;double W 0; public:Rectangle() default;Rectangle(double a, double b);double GetArea(); /*矩形面积*/double GetGirth(); /*矩形周长*/ }; /*构造函数*/ Rectangle::Rectangle(double a, double b) …...

代码随想录打卡第五十八天|● 583. 两个字符串的删除操作 ● 72. 编辑距离
583. 两个字符串的删除操作 题目: 给定两个单词 word1 和 word2 ,返回使得 word1 和 word2 相同所需的最小步数。 每步 可以删除任意一个字符串中的一个字符。 题目链接: 583. 两个字符串的删除操作 解题思路: dp数组的含义&am…...

面试流程之——程序员如何写项目经验
在简历中介绍IT项目经验,你可以遵循以下步骤: 明确项目目标:首先,清晰地阐述项目的目标。这可以是提升某个软件的性能,改进某个系统的用户界面,或者增加某款产品的功能。让读者了解你的工作与项目的整体目…...
框架安全-CVE 漏洞复现DjangoFlaskNode.jsJQuery框架漏洞复现
目录 服务攻防-框架安全&CVE复现&Django&Flask&Node.JS&JQuery漏洞复现中间件列表介绍常见语言开发框架Python开发框架安全-Django&Flask漏洞复现Django开发框架漏洞复现CVE-2019-14234(Django JSONField/HStoreField SQL注入漏洞ÿ…...
基于SSM的理发店管理系统
基于SSM的理发店管理系统的设计与实现~ 开发语言:Java数据库:MySQL技术:SpringSpringMVCMyBatis工具:IDEA/Ecilpse、Navicat、Maven 系统展示 主页 公告信息 管理员界面 用户界面 摘要 基于SSM(Spring、Spring MVC、…...
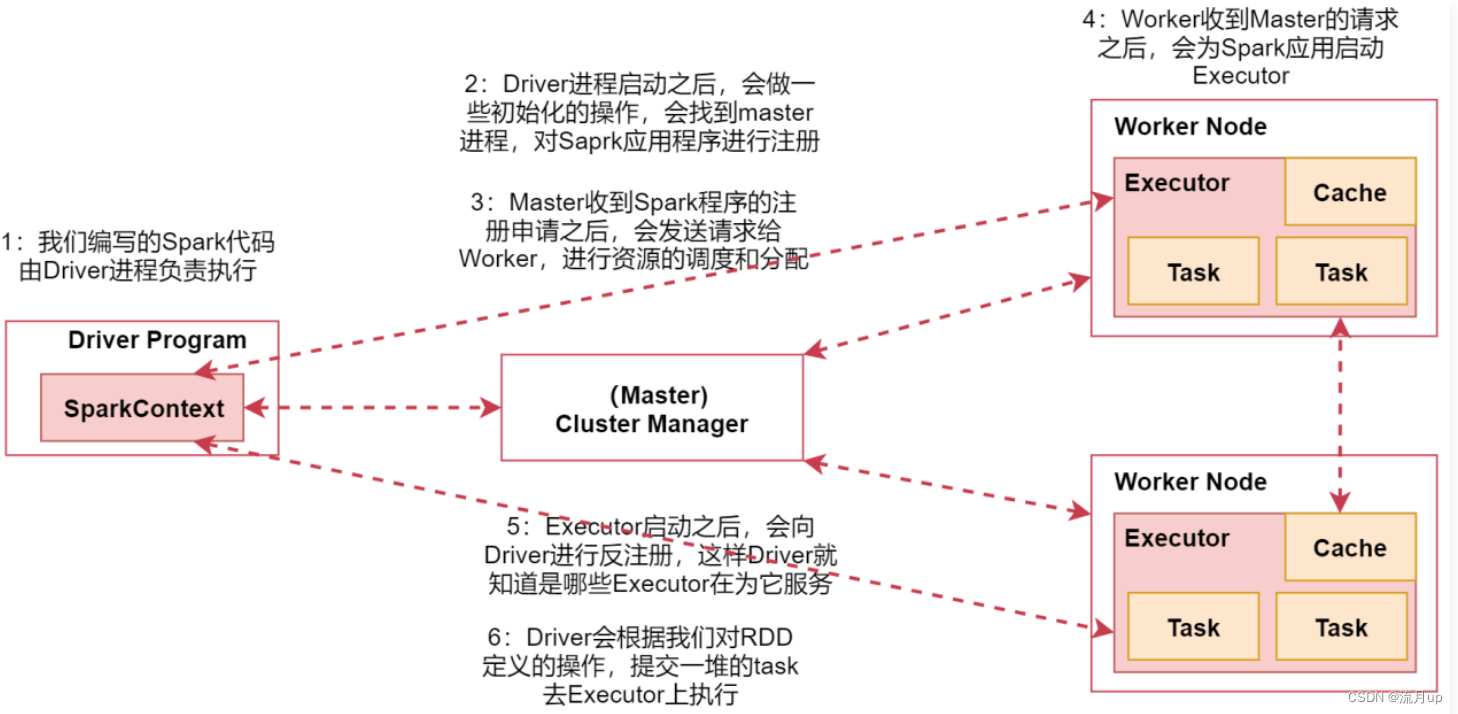
2.Spark的工作与架构原理
概述 目标: spark的工作原理spark数据处理通用流程rdd 什么是rddrdd 的特点 spark架构 spark架构相关进程spark架构原理 spark的工作原理 spark 的工作原理,如下图 图中中间部分是spark集群,也可以是基于 yarn 的,图上可以…...
qt-C++笔记之带有倒计数显示的按钮,计时期间按钮锁定
qt-C笔记之带有倒计数显示的按钮,计时期间按钮锁定 code review! 文章目录 qt-C笔记之带有倒计数显示的按钮,计时期间按钮锁定1.运行2.main.cc3.main.pro 1.运行 2.main.cc 代码 #include <QApplication> #include <QPushButton> #includ…...
有哪些?)
HTML全局属性(global attribute)有哪些?
HTML全局属性是指在HTML元素上可用的基本属性,它们适用于所有HTML元素。以下是一些常见的HTML全局属性: 1:class:为元素指定一个或多个类名,用于与CSS样式表关联。 2:id::为元素指定唯一的标识…...

MyBatis-Plus返回getOne返回null疑惑
getOne返回null 问题描述分析过程总结 问题描述 在数据库建了一张表主要包括两个字段master_id和slave_id;主要的额外字段max_lots 默认值是null; 当调用getOne进行查询结果是null,但实际情况是数据库时应该返回值的; AotfxMasterSlave ex…...
Physics2DPlugin3加载后会跳转gsap官网解决
因工作需要使用Physics2DPlugin3库,目标效果 加载他里面的在线js,使用效果正常,但是几秒会跳转官网,我们app内部、浏览器都会这样。 于是研究js代码,发现里面有setTimeout跳转。 删掉就好了 分享我改好的文件&#x…...
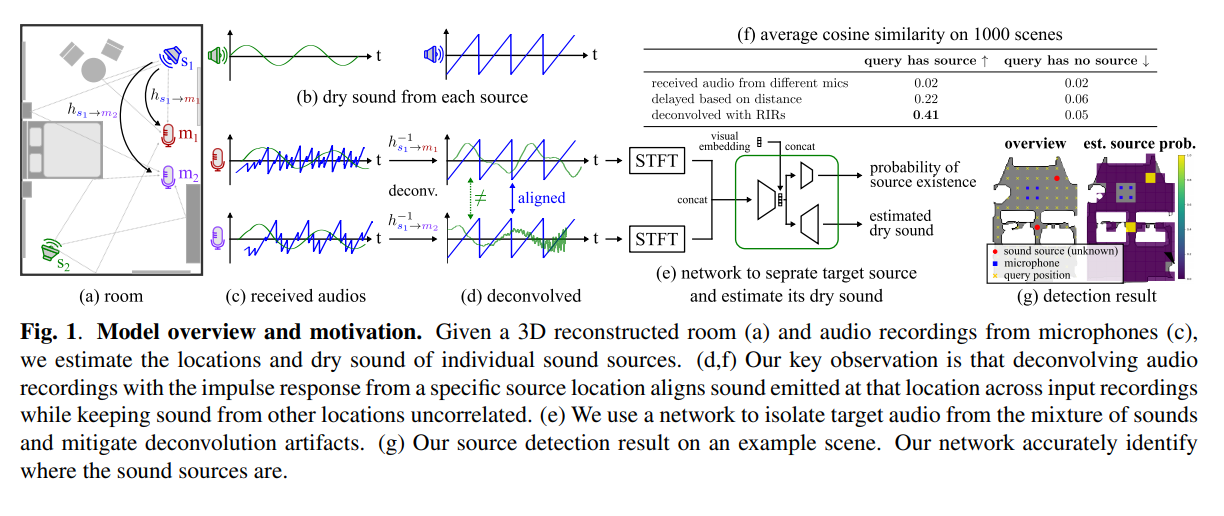
【AI视野·今日Sound 声学论文速览 第三十二期】Tue, 24 Oct 2023
AI视野今日CS.Sound 声学论文速览 Tue, 24 Oct 2023 Totally 20 papers 👉上期速览✈更多精彩请移步主页 Interesting: 📚nvas3d, 基于任意录音和室内3D信息合成重建不同听角(位置)处的新的声音。(from apple cmu) website: htt…...

在Linux上编译gdal3.1.2指南
作者:朱金灿 来源:clever101的专栏 为什么大多数人学不会人工智能编程?>>> 以Ubuntu 18编译gdal3.1.2为例,编译gdal3.1.2需要先编译proj库和geos库(可选)。我选择的proj库版本为proj-7.1.0,编译proj-7.1.0需要先编译tiff库和sqlite3。我选择的sqlite3的版本为…...

73. 矩阵置零 --力扣 --JAVA
题目 给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。 解题思路 通过二层循环找出元素为0所在的行和列;设置标志位记录当前行是否存在元素为0的,设置列表存储列为0的列&#…...
Kotlin——Android封装ViewBinding之二 优化)
(笔记)Kotlin——Android封装ViewBinding之二 优化
0. 在app模块的build.gradle文件中添加如下配置开启ViewBinding android {.......viewBinding {enabled true}} 1. 新建一个Ext.kt文件 添加两个扩展函数,分别对应Activity和Fragment inline fun <T : ViewBinding> AppCompatActivity.viewBinding(cross…...
(八))
MATLAB算法实战应用案例精讲-【图像处理】机器视觉(基础篇)(八)
目录 前言 几个高频面试题目 机器视觉如何获取到好图像 常见的视觉光源 各种视觉打光方式...

由k8s升级慢引起的etcd性能不足的问题排查
一、基本介绍 最近etcd查看出现性能 curl --cacert /path/to/etcdctl-ca.crt --cert /path/to/etcdctl.crt --key /path/to/etcdctl.key https://:2379/metrics | grep etcd_disk_wal_fsync_duration_seconds_bucket 当集群规模突破过大时规模时,曾出现如下性能瓶颈问题: etc…...
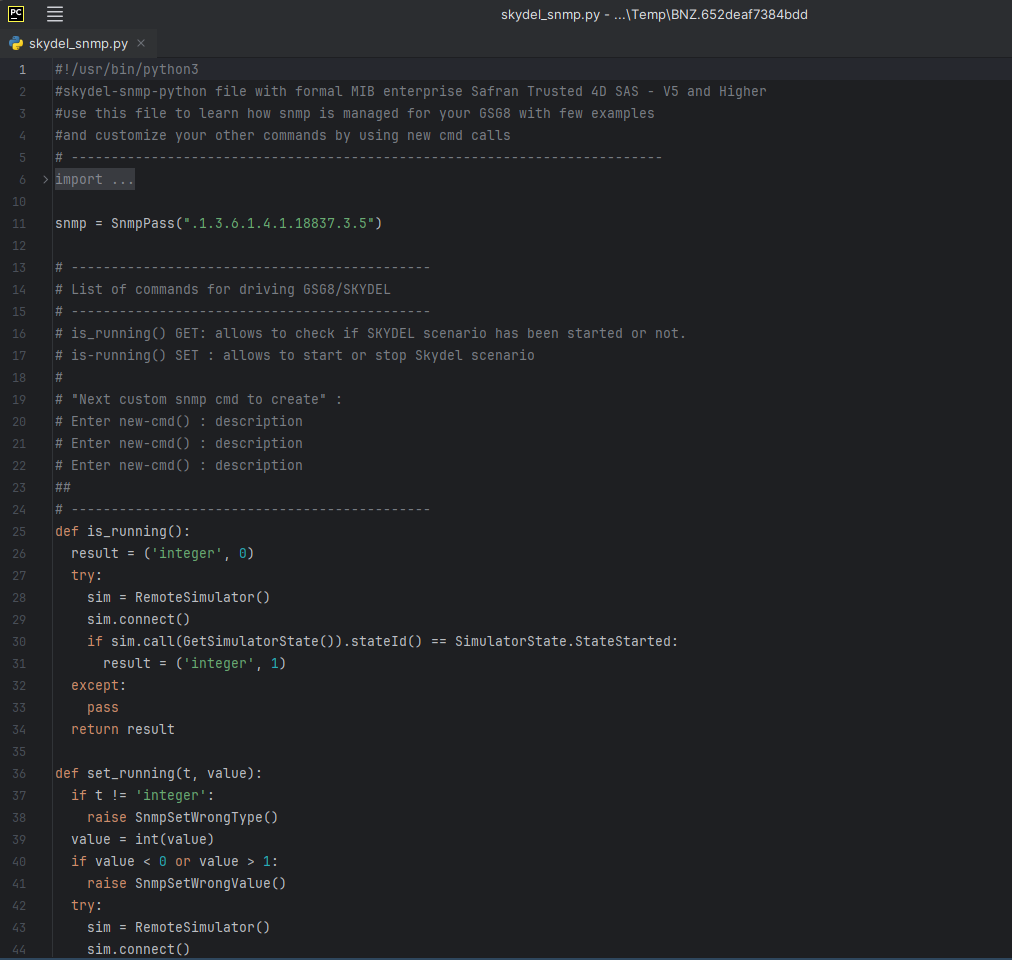
如何构建用于Skydel GNSS模拟仿真的SNMP代理方式?
使用Skydel API构建测试方案 凭借其现代、强大且直观的API,德思特Safran GNSS模拟引擎Skydel免费提供了Python、C#、C和Labview的开源客户端库,它具有600多条命令,并且有完善的文档与记录。 随着Skydel软件更新添加新功能,API得…...
vue2+ant-design-vue a-form-model组件二次封装(form表单组件)FormModel 表单
一、效果图 二、参数配置 1、代码示例 <t-antd-form:ref-obj.sync"formOpts.ref":formOpts"formOpts":widthSize"1":labelCol"{ span:2}":wrapperCol"{ span:22}"handleEvent"handleEvent" />2. 配置参数…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

k8s从入门到放弃之Pod的容器探针检测
k8s从入门到放弃之Pod的容器探针检测 在Kubernetes(简称K8s)中,容器探测是指kubelet对容器执行定期诊断的过程,以确保容器中的应用程序处于预期的状态。这些探测是保障应用健康和高可用性的重要机制。Kubernetes提供了两种种类型…...

Ray框架:分布式AI训练与调参实践
Ray框架:分布式AI训练与调参实践 系统化学习人工智能网站(收藏):https://www.captainbed.cn/flu 文章目录 Ray框架:分布式AI训练与调参实践摘要引言框架架构解析1. 核心组件设计2. 关键技术实现2.1 动态资源调度2.2 …...

华为云Flexus+DeepSeek征文 | 基于Dify构建具备联网搜索能力的知识库问答助手
华为云FlexusDeepSeek征文 | 基于Dify构建具备联网搜索能力的知识库问答助手 一、构建知识库问答助手引言二、构建知识库问答助手环境2.1 基于FlexusX实例的Dify平台2.2 基于MaaS的模型API商用服务 三、构建知识库问答助手实战3.1 配置Dify环境3.2 创建知识库问答助手3.3 使用知…...
数据可视化交互
目录 【实验目的】 【实验原理】 【实验环境】 【实验步骤】 一、安装 pyecharts 二、下载数据 三、实验任务 实验 1:AQI 横向对比条形图 代码说明: 运行结果: 实验 2:AQI 等级分布饼图 实验 3:多城市 AQI…...
