P4345 [SHOI2015] 超能粒子炮·改 题解---------Lucas定理
题面:
题目
题意概括: T T T 次询问,每次给出 n , k n,k n,k,求 ∑ i = 0 k C n i % 2333 \sum_{i = 0}^{k} C_{n}^{i} \ \% \ 2333 ∑i=0kCni % 2333。 1 ≤ T ≤ 1 0 5 , 1 ≤ n , k ≤ 1 0 18 1\leq T \leq10^5,1\leq n,k \leq 10^{18} 1≤T≤105,1≤n,k≤1018。
分析:
看到 模数是质数 并且组合数的上下标都很大,可以想到 Lucas 定理。我们根据取模后的到的余数对这 k k k 个位置进行分类,然后计算贡献。
当 k ≥ m o d k \geq mod k≥mod 时:
r e s = ∑ u = 0 m o d − 1 ∑ i = 0 ⌊ k + 1 m o d ⌋ − 1 C n u + i × m o d + g e t ( n , ⌊ k + 1 m o d ⌋ , ⌊ k + 1 m o d ⌋ × m o d , k ) \Large res = \sum_{u=0}^{mod-1}\sum_{i = 0}^{\left \lfloor \frac{k + 1}{mod} \right \rfloor - 1} C_{n}^{u + i\times mod} + get(n,\left \lfloor \frac{k + 1}{mod} \right \rfloor , \left \lfloor \frac{k + 1}{mod} \right \rfloor \times mod, k) res=∑u=0mod−1∑i=0⌊modk+1⌋−1Cnu+i×mod+get(n,⌊modk+1⌋,⌊modk+1⌋×mod,k)
= ∑ u = 0 m o d − 1 C n u × ∑ i = 0 ⌊ k + 1 m o d ⌋ − 1 C n m o d i + g e t ( n , ⌊ k + 1 m o d ⌋ , ⌊ k + 1 m o d ⌋ × m o d , k ) \Large \;\;\;\;\;\;=\sum_{u=0}^{mod-1}C_{n}^{u} \times \sum_{i = 0}^{\left \lfloor \frac{k + 1}{mod} \right \rfloor - 1}C_{\frac{n}{mod}}^{i} + get(n,\left \lfloor \frac{k + 1}{mod} \right \rfloor , \left \lfloor \frac{k + 1}{mod} \right \rfloor \times mod, k) =∑u=0mod−1Cnu×∑i=0⌊modk+1⌋−1Cmodni+get(n,⌊modk+1⌋,⌊modk+1⌋×mod,k)
其中 g e t ( n , c n t , s t , e d ) = ∑ i = s t e d C n i get(n, cnt, st, ed) = \sum_{i = st}^{ed} C_{n}^{i} get(n,cnt,st,ed)=∑i=stedCni。 e d − s t + 1 < m o d ed - st + 1< mod ed−st+1<mod。 c n t cnt cnt 是为了方便计算传上去的。
我们发现,计算 ∑ i = 0 ⌊ k + 1 m o d ⌋ − 1 C n m o d i \Large \sum_{i = 0}^{\left \lfloor \frac{k + 1}{mod} \right \rfloor - 1}C_{\frac{n}{mod}}^{i} ∑i=0⌊modk+1⌋−1Cmodni 又转化成了一个子问题。并且上下界都会除以 m o d mod mod,所以减小的会很快。
当 k < m o d k < mod k<mod 时:
r e s = ∑ i = 0 k C n i \Large res = \sum_{i = 0}^{k} C_{n}^{i} res=∑i=0kCni。
如果按照上面的式子去做,那么时间复杂度是 O ( T × m o d ) O(T \times mod) O(T×mod) 的。
因为 O ( T × m o d ) O(T \times mod) O(T×mod) 是过不去的。 瓶颈在于第一种情况中枚举 u u u 和计算 g e t get get 函数,以及第二种情况中枚举 i i i。它们的复杂度是 O ( m o d ) O(mod) O(mod) 的。我们考虑优化。
现在问题转变成了如何快速的求出 ∑ i = 0 k C n i , k < m o d \Large \sum_{i = 0}^{k} C_{n}^{i},k < mod ∑i=0kCni,k<mod 以及 快速求出 ∑ i = s t e d C n i , e d − s t + 1 < m o d \Large \sum_{i = st}^{ed} C_{n}^{i}, ed -st + 1 < mod ∑i=stedCni,ed−st+1<mod。
1.
对于 ∑ i = 0 k C n i \Large \sum_{i = 0}^{k} C_{n}^{i} ∑i=0kCni
我们考虑用 L u c a s Lucas Lucas 计算的时候, C n i = C n % m o d i % m o d × C n m o d i m o d \Large C_{n}^{i} = C_{n \%mod}^{i\%mod} \times C_{\frac{n}{mod}}^{\frac{i}{mod}} Cni=Cn%modi%mod×Cmodnmodi。
因为 i < m o d i < mod i<mod,所以 C n i = C n % m o d i × C n m o d 0 = C n % m o d i \Large C_{n}^{i} = C_{n \% mod}^{i} \times C_{\frac{n}{mod}}^{0} = C_{n \% mod}^{i} Cni=Cn%modi×Cmodn0=Cn%modi。
我们直接预处理出来 C i j , 0 ≤ j ≤ i < m o d \Large C_{i}^{j}, 0 \leq j \leq i < mod Cij,0≤j≤i<mod,以及 S i j = ∑ k = 0 j C i k \Large S_{i}^{j} = \sum_{k = 0}^{j} C_{i}^{k} Sij=∑k=0jCik。
那么 ∑ i = 0 k C n i = S n % m o d m i n ( k , n % m o d ) \Large \sum_{i = 0}^{k} C_{n}^{i} = S_{n \% mod}^{min(k, n \% mod)} ∑i=0kCni=Sn%modmin(k,n%mod), O ( 1 ) O(1) O(1) 调用就可以。
2.
对于 ∑ i = s t e d C n i , e d − s t + 1 < m o d \Large \sum_{i = st}^{ed} C_{n}^{i}, ed -st + 1 < mod ∑i=stedCni,ed−st+1<mod。
我们考虑此时 s t st st 一定是 m o d mod mod 的倍数,因为 s t st st 到 e d ed ed 是长度不到 m o d mod mod 的剩余那段。
有一个性质是 若 i , j < m o d i, j < mod i,j<mod, C n i + k × m o d \Large C_{n}^{i + k \times mod} Cni+k×mod 与 C n i \Large C_{n}^{i} Cni 的比值 和 C n j + k × m o d \Large C_{n}^{j + k \times mod} Cnj+k×mod与 C n j \Large C_{n}^{j} Cnj 的比值相同。 并且这个比值是 C n / m o d k \Large C_{n / mod}^{k} Cn/modk。这个可以用 Lucas 轻松证明。
那么问题就很简单了,我们求出 ∑ i = 0 e d − s t C n i \Large \sum_{i=0}^{ed-st}C_{n}^{i} ∑i=0ed−stCni,然后再乘上 C n / m o d k \Large C_{n/mod}^{k} Cn/modk 就好了。前面那个东西就是我们上面讨论的,后面那个可以用 L u c a s Lucas Lucas 定理在 l o g 2 n log_2n log2n 的时间复杂度内求出。
然后这道题就做完了,时间复杂度是 O ( T × l o g 2 n ) O(T \times log_2n) O(T×log2n)。
#include<bits/stdc++.h>// 找规律 好题啊
using namespace std;
typedef long long LL;
const LL mod = 2333;
int T;
LL n, k, inv[mod + 10], fac[mod + 10], c[mod + 10][mod + 10];
LL sum[mod + 10][mod + 10];
LL C(int n, int m){if(n < m) return 0;else return fac[n] * inv[m] % mod * inv[n - m] % mod;
}
LL Pow(LL x, LL y){LL res = 1, k = x % mod;while(y){if(y & 1) res = (res * k) % mod;y >>= 1;k = (k * k) % mod;}return res % mod;
}
LL Lucas(LL n, LL m){if(n < mod && m < mod) return C(n, m);else return C(n % mod, m % mod) * Lucas(n / mod, m / mod) % mod;
}
LL get(LL n, LL k, LL st, LL ed){if(st > ed) return 0;else{LL tmp = Lucas(n / mod, k);return tmp * sum[n % mod][min(ed - st, n % mod)] % mod;}
}
LL calc(LL n, LL k){// calc(n, k) = Σc[n][0] + c[n][1] + ... + c[n][k] k = min(k, n);// 取小的if(k < mod) return sum[n % mod][min(k, n % mod)];// k < mod 根据Lucas定理可知道, c[n][i] = c[n % mod][i % mod] * c[n / mod][i / mod] = c[n % mod][i] * c[n / mod][0] = c[n % mod][i] else return (sum[n % mod][n % mod] * calc(n / mod, (k + 1) / mod - 1LL) % mod + get(n, (k + 1) / mod, (k + 1) / mod * mod, k)) % mod;
}
int main(){fac[0] = 1LL;for(int i = 1; i < mod; i++) fac[i] = fac[i - 1] * (1LL * i) % mod;inv[mod - 1] = Pow(fac[mod - 1], mod - 2) % mod;for(int i = mod - 2; i >= 0; i--) inv[i] = inv[i + 1] * (1LL * (i + 1)) % mod;for(int i = 0; i <= mod - 1; i++){for(int j = 0; j <= i; j++){c[i][j] = C(i, j);if(!j) sum[i][j] = c[i][j] % mod;else sum[i][j] = (sum[i][j - 1] + c[i][j]) % mod;}}scanf("%d", &T);while(T--){scanf("%lld%lld", &n, &k);k = min(k, n);if(n < mod) printf("%lld\n", sum[n][k]);else{// n >= modprintf("%lld\n", calc(n, k));}}return 0;
}
相关文章:

P4345 [SHOI2015] 超能粒子炮·改 题解---------Lucas定理
题面: 题目 题意概括: T T T 次询问,每次给出 n , k n,k n,k,求 ∑ i 0 k C n i % 2333 \sum_{i 0}^{k} C_{n}^{i} \ \% \ 2333 ∑i0kCni % 2333。 1 ≤ T ≤ 1 0 5 , 1 ≤ n , k ≤ 1 0 18 1\leq T \leq10^5…...

http代理和ip代理的区别,代理IP带来了哪些好处?
随着互联网的快速发展,代理IP和HTTP代理已成为网络爬虫、网络营销、数据抓取等领域中不可或缺的一部分。但是,很多人在使用代理IP和HTTP代理时并不清楚两者的区别,以及代理IP所带来的好处。本文将详细介绍这两者之间的差异,以及代…...

浅谈电动汽车充电桩检测技术的实现
叶根胜 安科瑞电气股份有限公司 上海嘉定 201801 摘要: 关键词:电动直流和交流充电桩是我国电动汽车充电桩中运行量较大的一种。为了保持正常运行和使用,应高度重视检测、运行和维护工作。因此,有关部门应做好充电桩的检测工作…...

20 分钟搭建一个串流服务器
步骤1:准备Nginx RTMP容器 首先,您可以使用官方的Nginx RTMP Docker镜像来创建Nginx RTMP容器。运行以下命令: docker run -d -p 1935:1935 --name nginx-rtmp tiangolo/nginx-rtmp 这将在后台运行Nginx RTMP容器,将本地1935端…...

Android ActivityLifecycleCallback使用
在 Android 开发中,ActivityLifecycleCallbacks 是一个接口,用于监听和管理应用程序中 Activity 的生命周期事件。通过实现 ActivityLifecycleCallbacks 接口,可以在 Activity 的创建、启动、暂停、恢复、停止和销毁等各个阶段执行相应的操作…...

力扣labuladong——一刷day14
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、力扣21. 合并两个有序链表二、力扣86. 分隔链表三、力扣23. 合并 K 个升序链表四、力扣19. 删除链表的倒数第 N 个结点五、力扣876. 链表的中间结点六、力扣…...
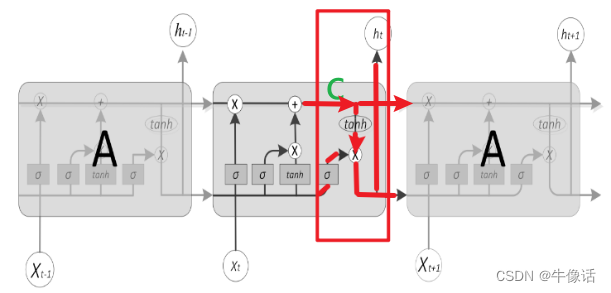
循环神经网络(RNN)与长短期记忆网络(LSTM)
前言: 通过前面的学习,我们以BP神经网络为基础,认识到了损失函数,激活函数,以及梯度下降法的原理;而后学习了卷积神经网络,知道图像识别是如何实现的。今天这篇文章,讲述的就是计算机…...

ArxDbgDocLockWrite 类简介
ArxDbgDocLockWrite 类是一个用于在 AutoCAD 中锁定文档的自定义类。它提供了一些方法来获取和释放对文档的写入锁定,并且还可以设置当前文档。 该类的原理如下: 构造函数 ArxDbgDocLockWrite() 和 ArxDbgDocLockWrite(AcDbDatabase* db) 用于创建 Arx…...

【教3妹学编辑-算法题】环和杆
3妹:2哥,今年春节的放假安排出来了,今年春节放8天假,我们公司除夕提前放一天,总共9天假。 耶~~~ 2哥 :你们公司这么好啊, 我们公司的放假安排还没出来,不知道今年除夕能不能回家了… 3妹&#x…...

解决 eslint 的 Parsing error: Unexpected token 错误
解决 eslint 的 Parsing error: Unexpected token 错误 问题描述:import动态导入,将js文件单独打包时,webpack打包错误 ERROR in ./src/js/main.js Module Error (from ./node_modules/_eslint-loader4.0.2eslint-loader/dist/cjs.js ): F…...

VR全景技术在文化展示与传播中有哪些应用?
引言: 随着科技的不断进步,虚拟现实(VR)全景技术已经成为文化展示与传播领域的一项重要工具。那么VR全景技术是如何改变文化展示与传播方式,VR全景技术又如何推动文化的传承和普及呢? 一.VR技术…...
Linux shell编程学习笔记19:until循环语句
Linux shell编程中的until语句,在功能上与其它编程语言一致,但在结构与其它编程语言又不太一样。在大多数编程语言中,until语句的循环条件表达式一般位于循环体语句的后面,但是在Linux shell编程中,until语句的循环条件…...
论文列表)
(CV)论文列表
CNN卷积神经网络之SKNet及代码 https://blog.csdn.net/qq_41917697/article/details/122791002 【CVPR2022 oral】MixFormer: Mixing Features across Windows and Dimensions 【精选】【CVPR2022 oral】MixFormer: Mixing Features across Windows and Dimensions-CSDN博客...
恶意软件防范和拦截: 提供防范恶意软件攻击的策略
恶意软件,或者俗称的“病毒”,一直是IT领域的一个严重威胁。这些恶意软件可以窃取敏感信息、损害系统稳定性,甚至对企业和个人造成重大经济损失。在这篇博客文章中,我们将讨论如何防范和拦截恶意软件攻击,包括使用反病…...

单例模式浅析
程序中仅存在一个对象实例,避免重复构建浪费资源。 1.饿汉式 主要分为3步:1.构造方法私有化 2.内部创建静态实例化对象 3.提供公有静态方法,返回对象实例 public class SingleTon { // 构造方法私有化private SingleTon(){} // 内部…...

Springboot引入mybatis-plus及操作mysql的json字段
springboot引入mybatis-plus,创建springboot项目省略 pom文件 <dependency><groupId>com.baomidou</groupId><artifactId>mybatis-plus-boot-starter</artifactId><version>3.4.3.4</version></dependency> <!…...
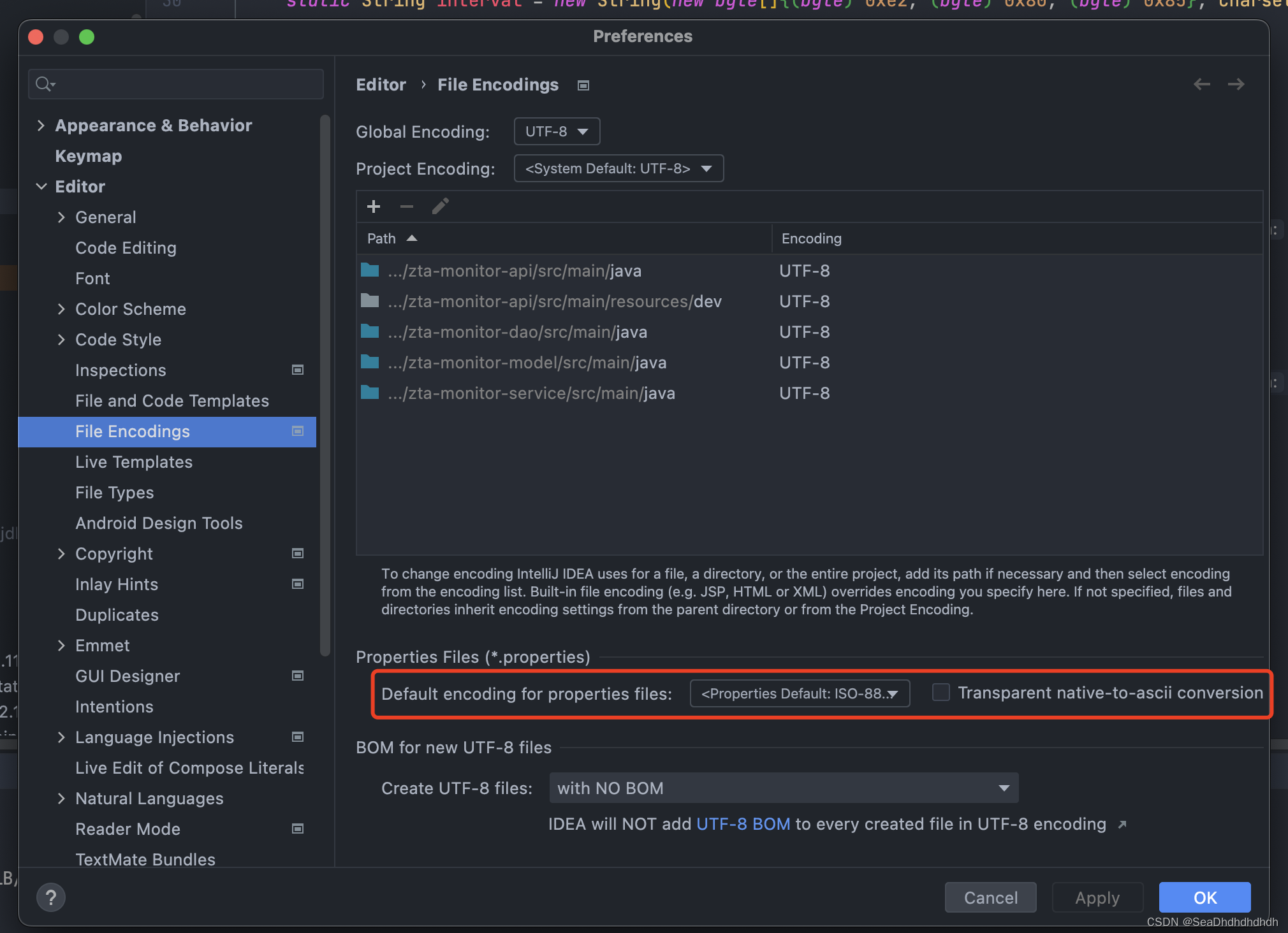
springboot读取application.properties中文乱码问题
目录 1 前言: 2 本地环境中的解决方案(以idea为例) 3 全部解决方案 1 前言: 初用properties,读取java properties文件的时候如果value是中文,会出现乱码的问题。我们首先需要明了乱码问题的根源。在 Java 中&#x…...
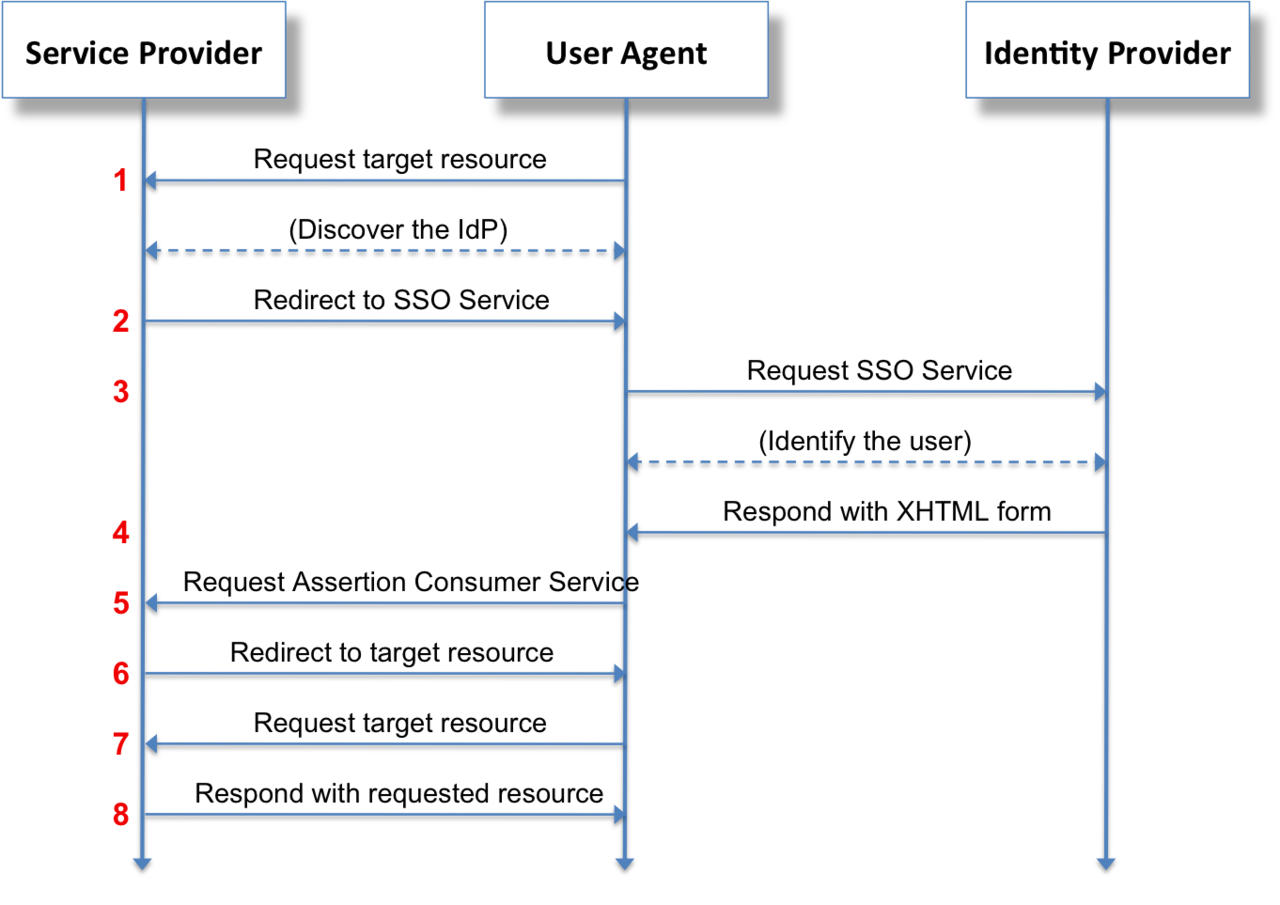
SAML- 安全断言标记语言
一、概念 安全断言标记语言(SAML)是一种开放标准,用于在各方之间(特别是身份提供商和服务提供商之间)交换身份验证和授权数据。SAML 是一种基于XML的安全断言标记语言(服务提供商用来做出访问控制决策的语句…...

【佳学基因检测】Node.js中http模块的使用
【佳学基因检测】Node.js中http模块的使用 先看代码: http.createServer(function (req, res) {res.writeHead(200, {Content-Type: text/html});res.end(测基因,阻遗传,就在佳学基因干(http://www.jiaxujiyin.com)!); }).liste…...
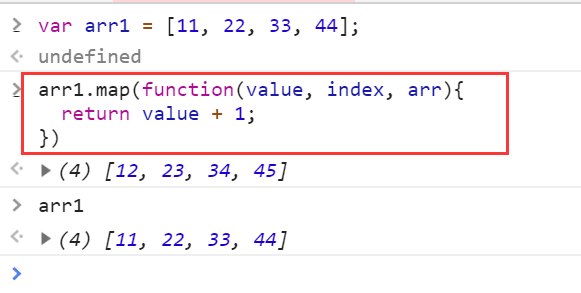
前端基础之JavaScript
JavaScript是一种能够在网页上添加交互效果的脚本语言,也被称为客户端语言。它可以在网页中操作HTML元素、改变CSS样式,以及处理用户的交互事件等。 以下是JavaScript的常见基础知识点: 变量和数据类型:JavaScript中的变量可以存…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...
