【蓝桥杯 第十届省赛Java B组】真题训练(A - H)H待更新
目录
A、组队 - 看图一眼出答案
B、不同子串 - 字符串模拟 + set去重
C、数列求值 - 模拟取余
D、数的分解 - 三重暴力
E、迷宫 - bfs 判断路径
F、特别数的和 - 弱智模拟
G、外卖店优先级 - map 暴力(90%通过率)
H、人物相关性分析 -
A、组队 - 看图一眼出答案

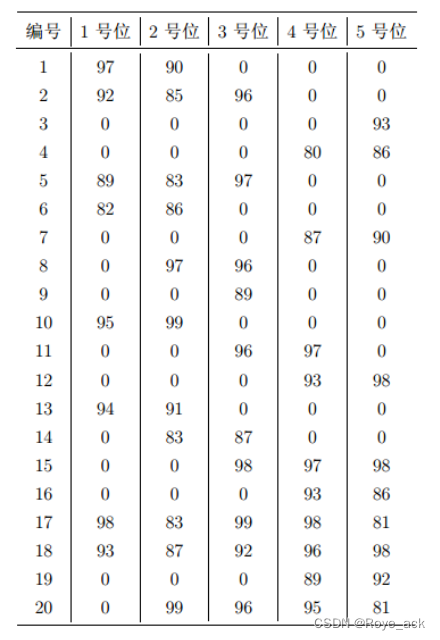
思路:
没啥说的,注意不能重复选择同一编号!
98+99+98+97+98=98*5=490
B、不同子串 - 字符串模拟 + set去重

import java.util.*;public class test {public static void main(String[] args){Scanner sc=new Scanner(System.in);String s="0100110001010001";int n=s.length();Set<String> st=new HashSet<>();for(int i=0;i<n;i++)for(int j=i+1;j<n+1;j++){String t=s.substring(i,j);st.add(t);}System.out.print(st.size());}
}
答案是100!
C、数列求值 - 模拟取余

思路:
最后算出来结果非常大,我们只需要每次取最后4位就好
答案是4659
public class test {static int N=20190324;public static void main(String[] args){Scanner sc=new Scanner(System.in);int[] d=new int[N];d[0]=1;d[1]=1;d[2]=1;for(int i=3;i<N;i++) d[i]=(d[i-1]+d[i-2]+d[i-3])%10000;System.out.print(d[N-1]);}
}D、数的分解 - 三重暴力

思路:
3个各不相同的正整数,我们只需要i j k三重循环,并保证i<j<k,再字符串判断是否含2或4即可,答案是40785
import java.util.Scanner;public class Main {public static void main(String[] args) {Scanner sc=new Scanner(System.in);int res=0,target=2019;for(int i=1;i<target;i++)for(int j=i+1;j<target;j++)for (int k=j+1;k<target;k++){if(i+j+k==target&&ck(i)&&ck(j)&&ck(k)) res++;}System.out.println(res);}public static boolean ck(int x) {String s=String.valueOf(x);if(s.indexOf('2')!=-1||s.indexOf('4')!=-1) return false;return true;}
}E、迷宫 - bfs 判断路径


【蓝桥杯集训11】BFS(4 / 4)_Roye_ack的博客-CSDN博客
思路:
DDDDRRURRRRRRDRRRRDDDLDDRDDDDDDDDDDDDRDRDRRURRUURRDDDDRDRRRRRURRRDRRDDDRRRRUURUUUUUUULULLUUUURRRRUULLLUUUULLUUULUURRURRURURRRDRDRRRRDRDRDDLLLDDRRDDRDDLDDDLLDDLLLDLDDDLDDRRRRRRRRRDDDDDDRR迷宫问题用bfs解决,要求满足字典序最小的最短路,我们可以设置能走时优先选择顺序【D>L>R>U】,也就是在dx dy方向数组上按顺序定义
建立坐标系,x轴正方向向下,y轴正方向向右
首先倒着bfs预处理出d[i][j]——(i,j)到终点的最短距离
然后正向遍历能走的点,如果d[x][y]==d[nx][ny]+1,说明走这点是在最短路上,记录方向
因为我们优先是【D>L>R>U】这么走的,所以输出的最短路肯定是字典序最小的
为什么d[x][y]==d[nx][ny]+1说明是在最短路上?
因为bfs跑完,处理出的 值非-1的d[i][j] 都是能通往终点的最短路。d[i][j]代表(i,j)到终点的最短距离,如果d[x][y]==d[nx][ny]+1,说明(x,y)是最短路上(nx,ny)的前一个点,相当于说(x,y)在最短路上
import java.util.Arrays;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;public class Main {static int n=30,m=50;static int[][] d=new int[n+1][m+1]; //d[i][j]是(i,j)到终点的最短距离static String[] g=new String[n+1]; //存储原始迷宫static int[] dx={1,0,0,-1}; // 方向优先D>L>R>Ustatic int[] dy={0,-1,1,0};static char[] dir={'D','L','R','U'};public static void main(String[] args) {Scanner sc=new Scanner(System.in);for(int i=0;i<n;i++) g[i]=sc.next();bfs();String res="";int x=0,y=0;while(x!=n-1||y!=m-1){for(int i=0;i<4;i++){int nx=dx[i]+x;int ny=dy[i]+y;if(nx>=0&&nx<n&&ny>=0&&ny<m&&g[nx].charAt(ny)=='0'){if(d[x][y]==d[nx][ny]+1){res+=dir[i]; //如果这条路能走且在最短路上 记录方向x=nx;y=ny;}}}}System.out.println("最短路径为:"+d[0][0]);System.out.println(res);}public static void bfs() {for(int i=0;i<n;i++) Arrays.fill(d[i],-1);d[n-1][m-1]=0;Queue<PII> q=new LinkedList<>();q.offer(new PII(n-1,m-1));while(!q.isEmpty()){PII t=q.poll();for(int i=0;i<4;i++){int nx=t.x+dx[i];int ny=t.y+dy[i];if(nx>=0&&nx<n&&ny>=0&&ny<m&&d[nx][ny]==-1&&g[nx].charAt(ny)=='0'){d[nx][ny]=d[t.x][t.y]+1;q.offer(new PII(nx,ny));}}}}
}class PII
{int x,y;PII(int x,int y){this.x=x;this.y=y;}
}F、特别数的和 - 弱智模拟

import java.util.Arrays;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;public class Main {public static void main(String[] args) {Scanner sc=new Scanner(System.in);int res=0;int n=sc.nextInt();for(int i=1;i<=n;i++)if(ck(i)) res+=i;System.out.println(res);}public static boolean ck(int x){String s=String.valueOf(x);if(s.indexOf('0')!=-1||s.indexOf('1')!=-1||s.indexOf('2')!=-1||s.indexOf('9')!=-1)return true;return false;}}
G、外卖店优先级 - map 暴力(90%通过率)



思路:
(碎碎念可以不看)这题折磨死我了,看一眼数据范围就知道双for会t,然后就想着找规律,但是找规律不行,第一次找的规律是:预处理记录每个id的时间点,2*时间点的个数=总共赚的优先级,然后再减去没有的时间点个数(因为如果没有订单优先级-1),最后判断大于3就说明在队列里
但这样写忽略了一种情况:id为2的时间点【5,6,6】如果按照上面规律,1,2,3,4属于没有出现的时间点,减去他们就是-4,然而实际上1,2,3,4时因为优先级为0,并不需要减去。
然后我就放弃思考了,写了个暴力……暴力写的完也是debug一年(因为循环时把t写成n了,为了这改了很久……)(碎碎念结束)
- 建一个map,【id:时间点列表】
- 然后遍历每一个id的从1—t的时间点
- 如果出现,则【优先级+=2×时间点出现次数】,这里运用排序+下标方法计算时间点出现次数
- 如果没有出现,则优先级-1,如果已经是0了就不变
- 最后判断一下状态,如果优先级>5则true,如果优先级<=3则false
- 如果状态为true,则res++
import java.util.*;public class Main {public static void main(String[] args) {Scanner sc=new Scanner(System.in);int res=0;int n=sc.nextInt(),m= sc.nextInt(), t= sc.nextInt();Map<Integer,List<Integer>> mp=new HashMap<>();int[] shopnum=new int[n+1];boolean[] st=new boolean[n+1];int[] h=new int[n+1];while(m-->0){int ts=sc.nextInt();int id=sc.nextInt();List<Integer> list=new ArrayList<>();if(shopnum[id]!=0) list=mp.get(id); //注意只有map中有list时才能直接赋值,否则需要新建list.add(ts);mp.put(id,list);shopnum[id]++;}int id=1;for(List<Integer> x:mp.values()){Collections.sort(x); //排序是为了后面计算一个时间点出现多次的情况for(int i=1;i<=t;i++){if(x.contains(i)) h[id]+=2*(x.lastIndexOf(i)-x.indexOf(i)+1); //eg:【1,1,1,3】 1的lastindex-indexof+1就是1的个数else if(!x.contains(i)) h[id]=Math.max(0,h[id]-1);if(h[id]>5) st[id]=true;else if(h[id]<=3) st[id]=false;}if (st[id]) res++;id++;}System.out.println(res);}
}
H、人物相关性分析 -



思路:
相关文章:

【蓝桥杯 第十届省赛Java B组】真题训练(A - H)H待更新
目录 A、组队 - 看图一眼出答案 B、不同子串 - 字符串模拟 set去重 C、数列求值 - 模拟取余 D、数的分解 - 三重暴力 E、迷宫 - bfs 判断路径 F、特别数的和 - 弱智模拟 G、外卖店优先级 - map 暴力(90%通过率) H、人物相关性分析 - A、组队 -…...

【牛客题】二进制求和 <模拟>
给定两个用字符串表示的二进制数,返回他们的和。 数据范围:字符串长度满足 1 ≤ n ≤ 1 0 5 10^5 105 ,字符串中只含有 0 和 1,且保证除 0 以外的二进制数没有前导零的情况。 示例输入: "101","1&qu…...

Error:Only idle or expired IP address can be disabled.
华为数通设备,在配置DHCP排除地址时可能会出现以下情况 Error:Only idle or expired IP address can be disabled. 这是因为地址已经被分配出去,所以现在无法进行排除 解决方法 1.先进入接口关闭DHCP [CE2-GigabitEthernet0/0/1]undo dhcp select g…...

Xubuntu16.04系统中create_ap开启5G网络的踩坑记录
Xubuntu16.04系统中安装create_ap创建无线AP: https://blog.csdn.net/qq_45445740/article/details/133972642?spm1001.2014.3001.5501 目录 1.create_ap.conf 配置文件解析2.关于信号强度和延时2.1 信号强度2.2 信号延时2.3 网络延时测试工具推荐——PingPlotter …...

8. 一文快速学懂常用工具——Linux命令(上)
本章讲解知识点 引言 指令学习 本专栏适合于软件开发刚入职的学生或人士,有一定的编程基础,帮助大家快速掌握工作中必会的工具和指令。本专栏针对面试题答案进行了优化,尽量做到好记、言简意赅。如专栏内容有错漏,欢迎在评论区指…...

@RestController注解说明
在Spring框架中,RestController注解是一个非常重要的注解,它用于将一个类标记为RESTful风格的控制器。本文将详细介绍RestController注解的作用和用法,并提供示例以帮助读者更好地理解和使用它。 RestController的作用 RestController注解是…...

Excel中行列范围的转换
将 行:1,4-5,8,11 列:a,c-e,f 这种写法转换成单元格地址的方法。 public static Tuple<List<int>, List<string>> ConvertRowColumn(string rowRep, string colRep){List<int> rowIdxs new List<int>();rowRep rowRep.…...

golang的类型断言
前言:原因很简单,写的代码panic了。报错如下。为此专门看下golang的类型断言。 “[PANIC]interface conversion: interface {} is string, not float64”。 1、类型断言(assertion) 所谓“类型断言”即判断一个变量是不是某个类型的实例(简单来讲就是判…...

监听dom变化,监听dom属性变化
一、利用new MutationObserver const config {attributes: true, // 监听属性变化childList: true, // 监听子节点变subtree: true // 监听后代元素变化};jianting new MutationObserver(() > {this.changeFun()});jianting.observe(dom, config) /监听 jianting.disconne…...

mfc140u.dll丢失怎么修复,mfc140u.dll文件有什么作用
今天我想和大家分享的是关于mfc140u.dll文件丢失的解决方法。在我们使用电脑的过程中,有时候会遇到一些错误提示,其中比较常见的就是“无法找到mfc140u.dll文件”。那么,这个文件是什么呢?它有什么作用呢? 首先&#…...

关于MySql update语句不能用子查询的解决办法
关于MySql update语句不能用子查询的解决办法 使用MySql数据库语法操作update时,第一时间想到的是一下写法: UPDATE purchase_request_detail SET convert_to_voucher_id2, convert_to_voucher_typeinventory-voucher WHERE detail_id IN (select deta…...

【WinForm】WinForm程序C#分屏显示
文章目录 前言1. 准备工作2. 步骤3 示例代码4. 结论 前言 在开发WinForm应用程序时,有时我们需要在另一个屏幕上显示与主界面内容相同的界面。本文将介绍如何使用C#克隆正在运行的界面,并在另一个屏幕上显示相同的内容。 1. 准备工作 在开始之前&…...
云安全—K8S API Server 未授权访问
0x00 前言 master节点的核心就是api服务,k8s通过REST API来进行控制,在k8s中的一切都可以抽象成api对象,通过api的调用来进行资源调整,分配和操作。 通常情况下k8s的默认api服务是开启在8080端口,如果此接口存在未授…...
nodejs+vue啄木鸟便民维修网站设计与实现-计算机毕业设计python-django-php
1、目的: 设计一个适用于便民家电维护的平台。该系统方便管理员对用户信息的管理,使用户在不掌握任何专业知识的前提下,可以方便快速的上手,因此项目应具有广泛使用人群。该课题应包括(至少包括)以下几个基…...
【数据结构】树形结构所有路径复原为链表
目录 1. 树形结构可视化 2. 树形结构转为链表 此目标是要还原树形结构的所有路径。树形结构是一种常见的数据结构,它表示元素之间层次关系。在树形结构中,每个节点可能拥有一个或多个子节点,形成了一个分层的结构。为了还原树形结构的路径&…...
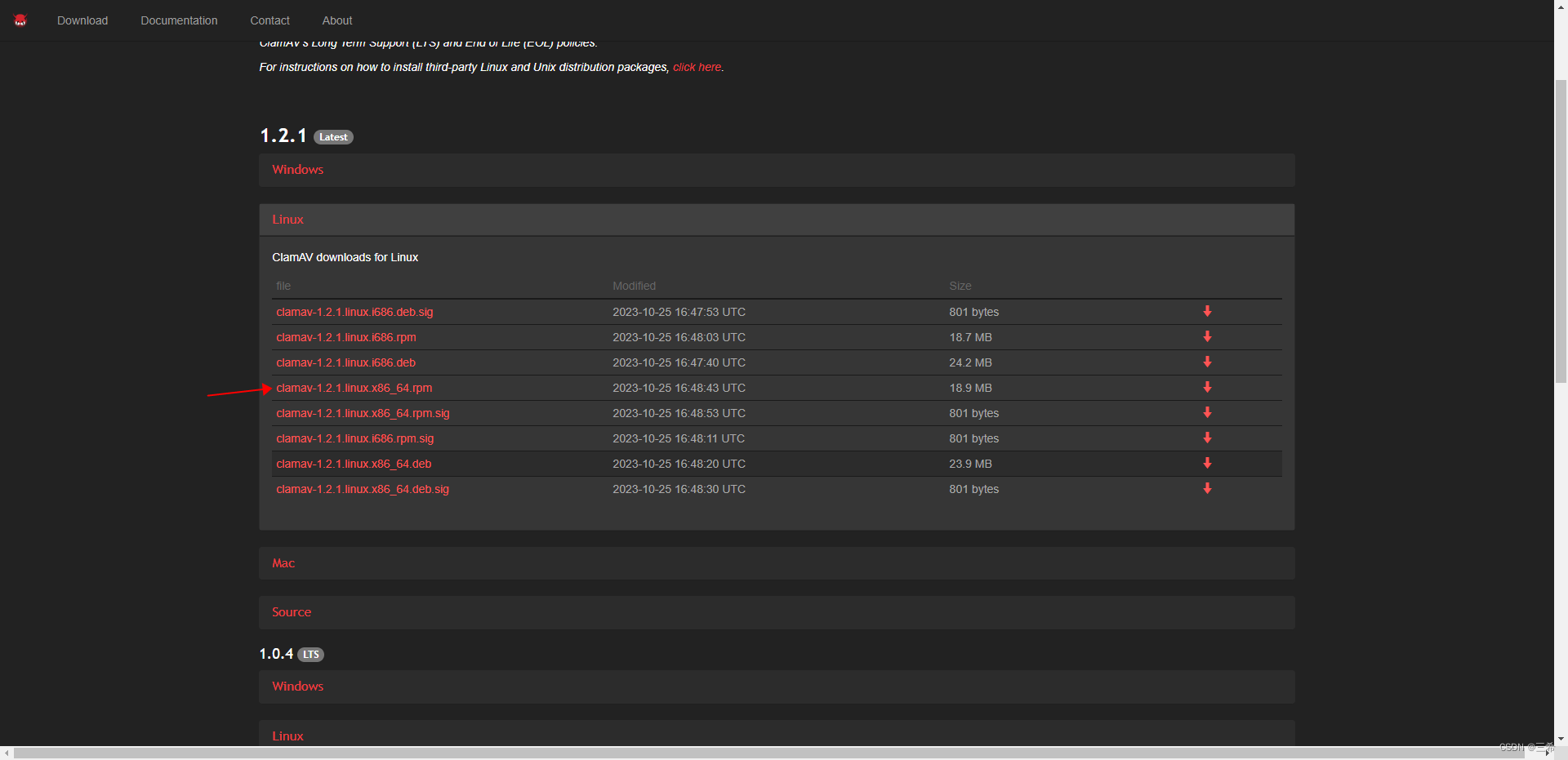
linux杀毒软件下载、安装(在线安装、离线安装)
下载 ClamAVNet 离线安装 # 离线安装 rpm -ivh --prefix/usr/local/clamav clamav*linux.x86_64.rpm # 添加用户组和组成员 groupadd clamav useradd -g clamav clamav # 创建日志目录、病毒库目录和套接字目录 mkdir -p /usr/local/clamav/logs mkdir -p /usr/local/clamav/…...
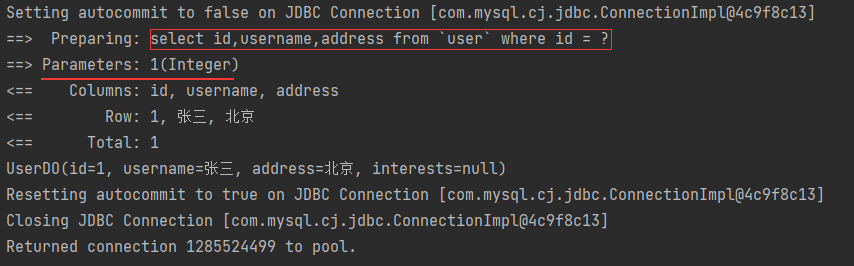
系列五、映射文件xxxMapper.xml
一、概述 mapper映射文件是mybatis中最重要的部分,涉及到的细节也非常多。 1.1、parameterType 表示输入参数的类型。例如: <select id"getUserById" parameterType"integer" resultType"org.star.entity.model.UserDO&…...

【缓存】Spring全家桶中@CacheEvict无效情况共有以下几种
Spring全家桶中CacheEvict无效情况共有以下几种 一、背景介绍二、原因分析三、解决方案 一、背景介绍 SpringBoot中使用Cacheable注解缓存数据,使用CacheEvict注解删除缓存。但是在项目使用过程中,发现使用CacheEvict注解删除缓存无效。 拓展ÿ…...

P9117 [春季测试 2023] 涂色游戏
Portal. 维护每一行、每一列最后一次染色时染上的颜色以及时间戳即可。 时间复杂度 O ( T n ) O(Tn) O(Tn)。 #include <bits/stdc.h> using namespace std;const int maxn1e55; struct node{int c,t;}a[maxn],b[maxn];void solve() {int n,m,q;cin>>n>>…...

react如何进行项目配置代理
目录 一、前言 二、配置方法 三、总结 前言: 在使用React创建应用程序时,配置代理的目的是为了解决跨域请求的问题。跨域请求是指在浏览器中,一个站点的Web应用程序向另一个不同域名的站点发送请求。由于浏览器的安全策略,这些…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...