P1284 三角形牧场
Portal.
首先,我们需要一些初中数学知识——秦九韶公式(又名海伦公式):
p = a + b + c 2 S = p ( p − a ) ( p − b ) ( p − c ) \begin{align} &p=\dfrac{a+b+c}{2}\\ &S=\sqrt{p(p-a)(p-b)(p-c)} \end{align} p=2a+b+cS=p(p−a)(p−b)(p−c)
假设 f ( k , i , j ) f(k,i,j) f(k,i,j) 表示前 k k k 个木板能否围成两边长为 i i i、 j j j 的三角形,状态转移时有三种情况:
- 把第 k k k 个木板加到边 i i i 中,前 k − 1 k-1 k−1 个木板要围成两边长为 i − l k i-l_k i−lk、 j j j 的三角形,即 f ( k − 1 , i − l k , j ) f(k-1,i-l_k,j) f(k−1,i−lk,j)。
- 把第 k k k 个木板加到边 j j j 中,同理 f ( k − 1 , i , j − l k ) f(k-1,i,j-l_k) f(k−1,i,j−lk)。
- 把第 k k k 个木板加到第三条边中, f ( k − 1 , i , j ) f(k-1,i,j) f(k−1,i,j)。
三者或运算之后的真假即结果。
可以观察到,转移过程中只跟前 k − 1 k-1 k−1 个木板的状态有关,所以我们可以采用背包的滚动数组思想,压掉 k − 1 k-1 k−1 这一层。
注意:
- 要用
double。 - 要反着枚举 i i i、 j j j,这要参考 01 01 01 背包的思想,如果正着枚举会重复使用某一条边,并且压掉的 k − 1 k-1 k−1 这一层循环不能保存之前的状态会被替代。
- 初始化: f ( 0 , 0 ) = 1 f(0,0)=1 f(0,0)=1。
代码如下:
#include <bits/stdc++.h>
using namespace std;int l[45];
bool f[805][805];
double ans;double work(double a,double b,double c)
{double p=(a+b+c)/2;return sqrt(p*(p-a)*(p-b)*(p-c));
}bool check(int a,int b,int c)
{if(a+b>c&&a+c>b&&b+c>a) return 1;return 0;
}int main()
{int n,cc,i,j,k;cin>>n;for(i=1;i<=n;i++) cin>>l[i],cc+=l[i];f[0][0]=1;for(k=1;k<=n;k++)for(i=cc/2;i>=0;i--)for(j=cc/2;j>=0;j--){if(i-l[k]>=0&&f[i-l[k]][j]) f[i][j]=1;else if(j-l[k]>=0&&f[i][j-l[k]]) f[i][j]=1;}ans=-1;for(i=cc/2;i>0;i--)for(j=cc/2;j>0;j--){if(!f[i][j]) continue;if(!check(i,j,cc-i-j)) continue;ans=max(ans,work(i,j,cc-i-j));}if(ans!=-1) cout<<(long long)(ans*100);else cout<<-1;return 0;
}
相关文章:

P1284 三角形牧场
Portal. 首先,我们需要一些初中数学知识——秦九韶公式(又名海伦公式): p a b c 2 S p ( p − a ) ( p − b ) ( p − c ) \begin{align} &p\dfrac{abc}{2}\\ &S\sqrt{p(p-a)(p-b)(p-c)} \end{align} p2abcSp(p…...
【Linux】:Linux开发工具之Linux编辑器vim的使用
🔫1.Linux编辑器-vim使用 📤 vi/vim的区别简单点来说,它们都是多模式编辑器,不同的是vim是vi的升级版本,它不仅兼容vi的所有指令,而且还有一些新的特性在里面。例如语法加亮,可视化操作不仅可以…...

PFMEA详解结构分析——Sun FMEA软件
FMEA从1949年诞生到今天已经发生过多次更新,最新版本是2019年6月发布的《AIAG VDA FMEA手册》。新手册借鉴了AIAG的方框图、参数图、流程图等工具的运用,也借鉴了VDA的五步过程导向法,并在此基础上头尾各增加一步,形成了FMEA七步法…...

Qt扫盲-QFutureWatcher理论总结
QFutureWatcher理论总结 一、概述二、转态 一、概述 QFutureWatcher类允许我们使用信号槽的方式去监控QFuture。 QFutureWatcher提供关于QFuture的信息和通知。使用 setFuture() 函数开始监视特定的QFuture。 future()函数通过setFuture()返回 QFuture 集合。 为了方便起见…...
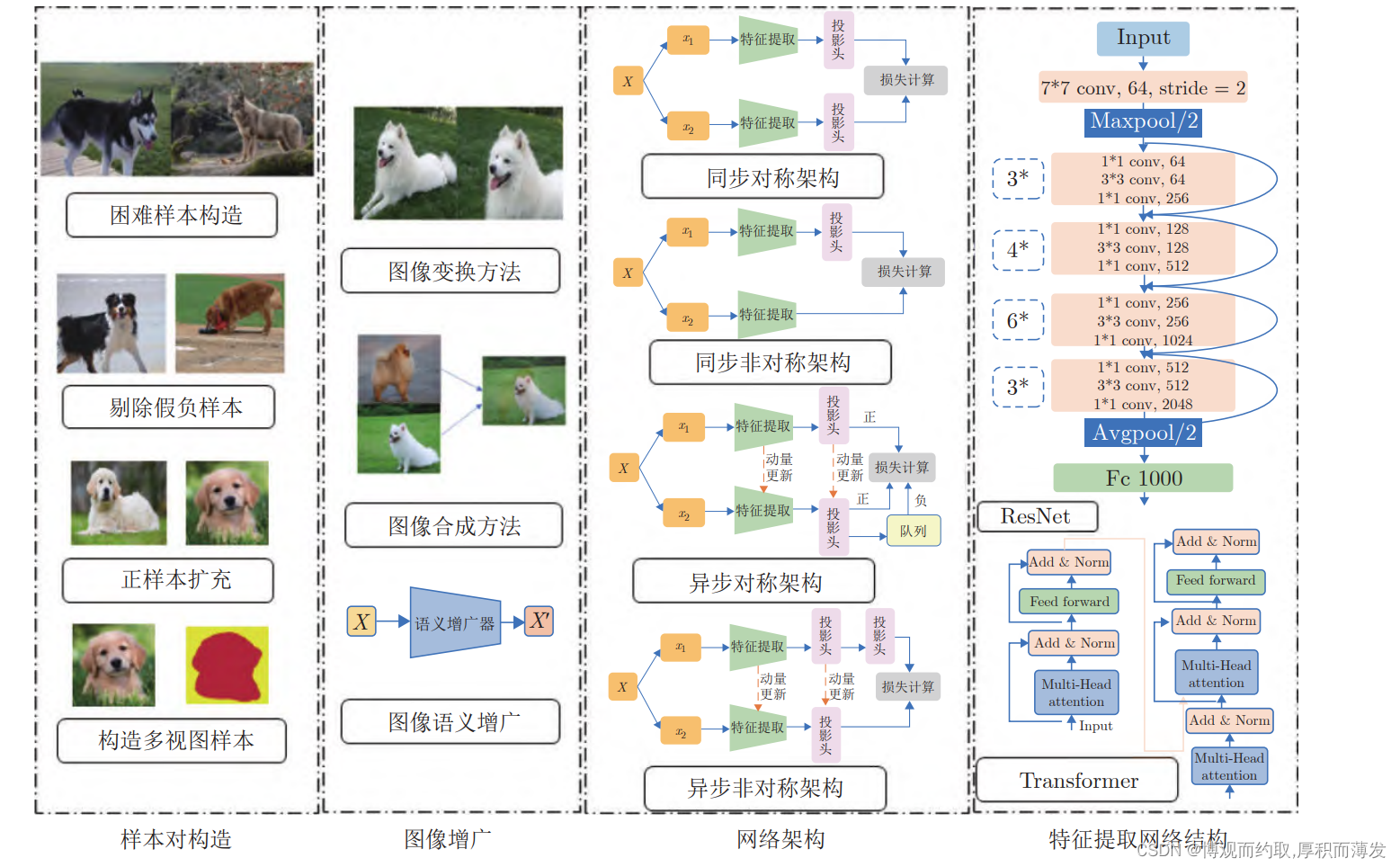
对比学习(contrastive Learning)
起源和定义 自监督学习又可以分为对比学习(contrastive learning)和生成学习(generative learning)两条主要的技术路线。 比学习的核心思想是将正样本和负样本在特征空间对比,从而学习样本的特征表示,使得样本与正样本的特征表示尽可能接近。正样本和负…...
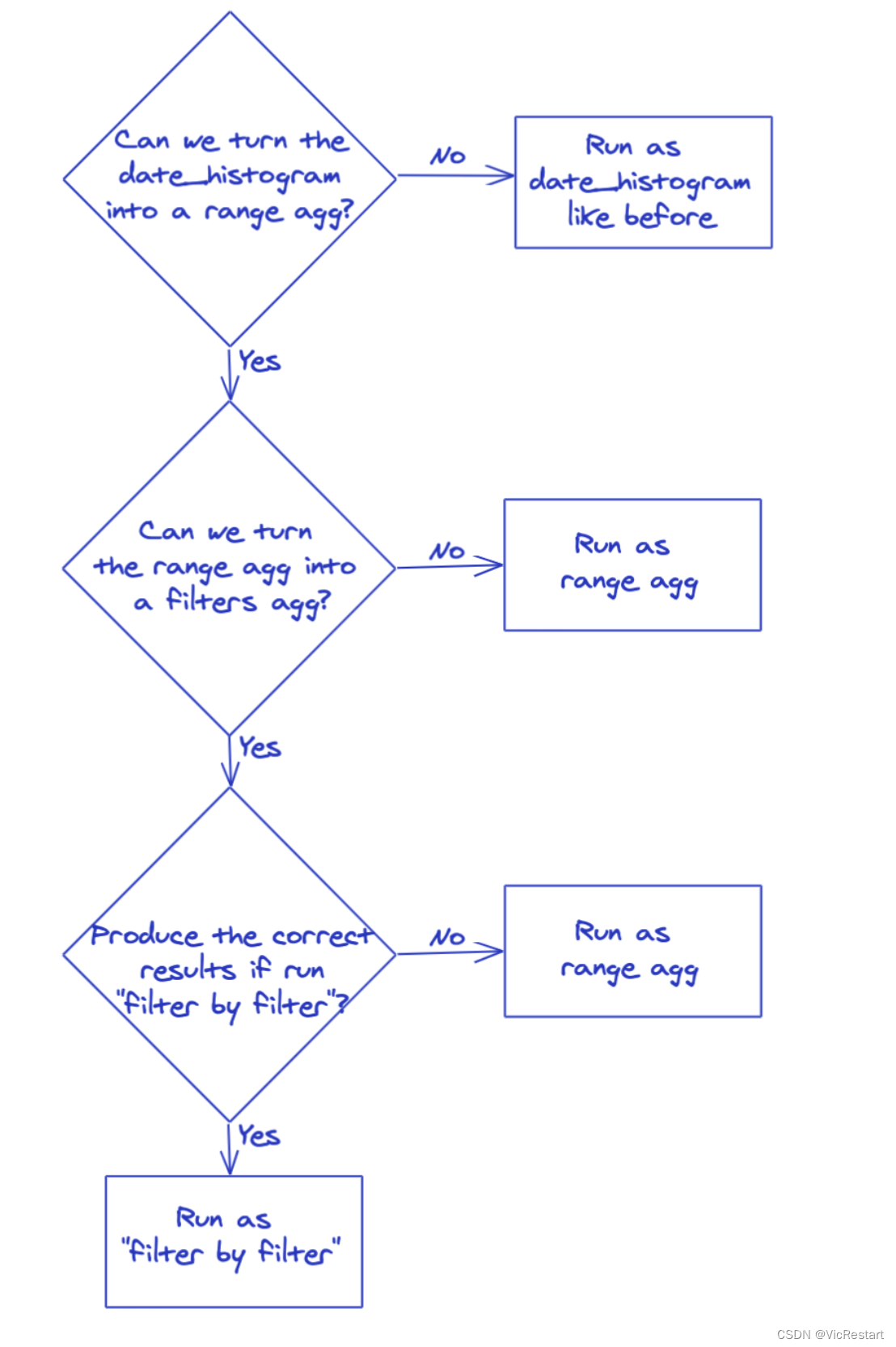
译文:我们如何使 Elasticsearch 7.11 中的 date_histogram 聚合比以往更快
这篇文章是ES7.11版本的文章,主要学习的是思路,记录在这里留作以后参考用。 原文地址:https://www.elastic.co/cn/blog/how-we-made-date-histogram-aggregations-faster-than-ever-in-elasticsearch-7-11 正文开始: Elasticsea…...

python设计模式4:适配器模式
使用适配器模式使用两个或是多个不兼容的接口兼容。在不修改不兼容代码的情况下使用适配器模式实现接口一致性。通过Adapter 类实现。 例子: 一个俱乐部类Club,艺术加被请到俱乐部在表演节目: organize_performance()…...
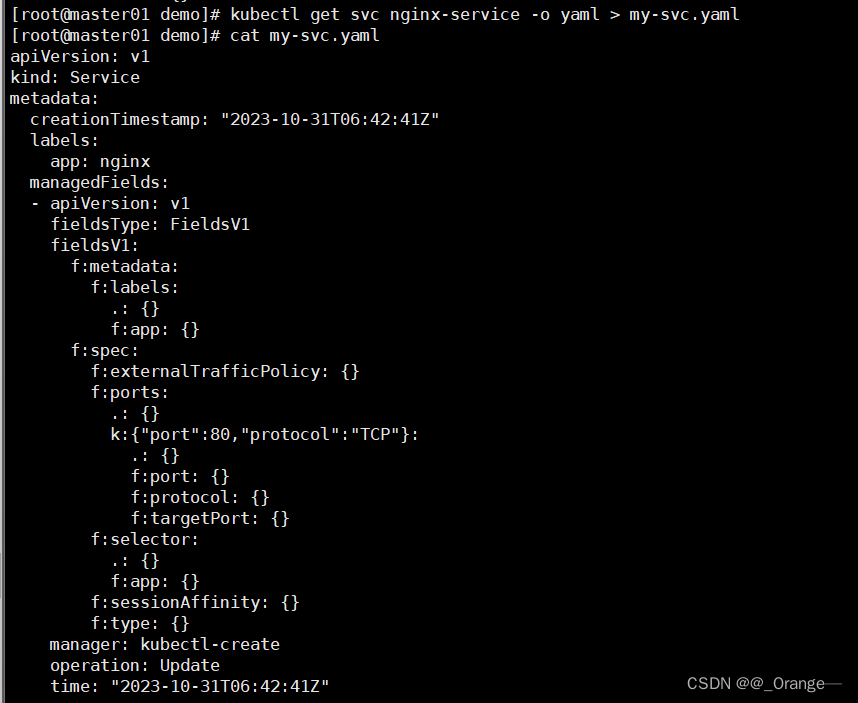
kubectl资源管理命令---声明式
目录 一、yaml和json介绍 1、yuml语言介绍 2、k8s支持的文件格式 二、声明式对象管理 1、deployment.yaml文件详解 2、Pod yaml文件详解 3、Service yaml文件详解 三、编写资源配置清单 1、 编写yaml文件 2、 创建并查看pod资源 3、创建service服务对外提供访问并测试…...
IDEA使用-通过Database面板访问数据库
文章目录 前言操作过程注意事项1.无法下载驱动2.“Database”面板不显示数据库表总结前言 作为一款强大IDE工具,IDEA具有很多功能,本文将以MariaDB数据库访问为例,详细介绍如何通过IDE工具的Database面板来访问数据库。 操作过程 不同的版本操作会略有差异,这里我们用于演…...

单片机如何写好一个模块的驱动文件
搞单片机,MCU:STM32/GD32/HC32,通讯模组:4G/WIFI/BT/433,总线:USB/CAN/K/232/485,各种常见的传感器,都接触过。 一开始学习单片机的时候没有形成很好的编写习惯,如LED点亮/熄灭/闪烁…...

【C++笔记】C++多态
【C笔记】C多态 一、多态的概念及实现1.1、什么是多态1.2、实现多态的条件1.3、实现继承与接口继承1.4、多态中的析构函数1.5、抽象类 二、多态的实现原理 一、多态的概念及实现 1.1、什么是多态 多态的概念: 在编程语言和类型论中,多态(英…...

不想改代码!这样实现Reverse Sync测量时间同步精度
TSN的时间同步精度,指被测时钟与主时钟的最大偏差。在设备的组网过程中,最大的困难就是保证期望的时间同步精度。主时钟仅负责将自身的时间分发出去,难以判断其他设备的同步效果;此外,若在网络中某处发生了同步故障&am…...
【webrtc】 对视频质量的码率控制的测试与探索
目录 环境设置 transport-cc goog-remb (webrtc中的两种码率算法) 修改成remb算法 测试 效果 后续 可参考工程 环境设置 要到meshx上操作 telnet 112 然后执行factory_env show |grep meshx_ip 之后telnet meshx_ip 用户名admin 密码****.119 执行一下r…...

2003 - Can‘t connect to MysQL server on ‘39.108.169.0‘ (10060 “Unknown error“)
问题描述 某天和往常一样启动java项目,发现数据库出问题了,然后打开navicat,发现数据库的链接都连接不上, 一点击就会弹出报错框: 然后就各种上网搜索。 解决方案 上网查了一些解决方案,大部分都是说看…...

Python算法——选择排序
选择排序(Selection Sort)是一种简单的排序算法,它的基本思想是在未排序的部分中选择最小(或最大)的元素,然后将其放在已排序部分的末尾。选择排序不同于冒泡排序,它不需要反复交换元素…...

从「码农」到管理者,E人程序员的十年蜕变
点击文末“阅读原文”即可参与节目互动 剪辑、音频 / 卷圈 运营 / SandLiu 卷圈 监制 / 姝琦 封面 / 姝琦Midjourney 产品统筹 / bobo 场地支持 / 声湃轩北京录音间 当我们谈论程序员创业时,常常会首先想到一些传统观念认为的挑战:沟通技巧不佳、逻…...

ant Java任务的jvmargs属性和<jvmarg>内嵌元素
ant的Java任务可以在运行Apache Ant的Java虚拟机内、或者启用另外的Java虚拟机运行一个Java类。 可以使用java任务的jvmargs属性,设置传递给在新进程中的java虚拟机的参数。但当java任务的fork禁用的时候,jvmargs属性会被忽略。jvmargs这个属性已经被废…...

XML External Entity-XXE-XML实体注入
XML 实体? XML 实体允许定义标签,在解析 XML 文档时这些标签将被内容替换。一般来说,实体分为三种类型: 内部实体 外部实体 参数实体。 必须在文档类型定义(DTD)中创建实体 一旦 XML 文档被解析器处理,它将js用定义的常量“Jo Smith”替换定义的实体。正如您所看到…...

生态扩展Spark Doris Connector
生态扩展Spark Doris Connector doris官网去查找相匹配的spark spark的安装: tar -zxvf spark-3.1.2-bin-hadoop3.2.tgzmv spark-3.1.2-bin-hadoop3.2 /opt/sparkspark环境配置:vim /etc/profile export SPARK_HOME/opt/spark export PATH$PATH:$SPAR…...

构建 hive 时间维表
众所周知 hive 的时间处理异常繁琐且在一些涉及日期的统计场景中会写较长的 sql,例如:周累计、周环比等;本文将使用维表的形式降低时间处理的复杂度,提前计算好标准时间字符串未来可能需要转换的形式。 一、表设计 结合业务场景常…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

【Linux手册】探秘系统世界:从用户交互到硬件底层的全链路工作之旅
目录 前言 操作系统与驱动程序 是什么,为什么 怎么做 system call 用户操作接口 总结 前言 日常生活中,我们在使用电子设备时,我们所输入执行的每一条指令最终大多都会作用到硬件上,比如下载一款软件最终会下载到硬盘上&am…...

软件工程 期末复习
瀑布模型:计划 螺旋模型:风险低 原型模型: 用户反馈 喷泉模型:代码复用 高内聚 低耦合:模块内部功能紧密 模块之间依赖程度小 高内聚:指的是一个模块内部的功能应该紧密相关。换句话说,一个模块应当只实现单一的功能…...

yaml读取写入常见错误 (‘cannot represent an object‘, 117)
错误一:yaml.representer.RepresenterError: (‘cannot represent an object’, 117) 出现这个问题一直没找到原因,后面把yaml.safe_dump直接替换成yaml.dump,确实能保存,但出现乱码: 放弃yaml.dump,又切…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...
