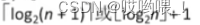数据结构详细笔记——二叉树
文章目录
- 二叉树的定义和基本术语
- 特殊的二叉树
- 满二叉树
- 完全二叉树
- 二叉排序树
- 平衡二叉树
- 二叉树的常考性质
- 完全二叉树的常考性质
- 二叉树的存储结构
- 顺序存储
- 链式存储
- 二叉树的先中后序遍历
- 先序遍历(空间复杂度:O(h))
- 中序遍历
- 后序遍历
- 应用
- 二叉树的层序遍历
- 由遍历序列构造二叉树
- 线索二叉树
- 线索二叉树的存储结构
- 二叉树的线索化
- 二叉树的线索化
二叉树的定义和基本术语
二叉树的基本概念
二叉树是n(n>=0)个结点的有限集合
①或者为空的二叉树,即n=0
②或者由一个根结点和两个互不相交的被称为根的左子树和右子树组成,左子树和右子树又分别是一颗二叉树
特点:
1、每一个结点至多只有两棵子树
2、左右子树不能颠倒(二叉树是有序树)
注意区别:度为2的有序树与二叉树的区别
度为2的树:肯定是非空树,所有结点的度<=2,至少有一个结点的度为2
二叉树:可以为空树,所有的结点只要<=2就可
特殊的二叉树
满二叉树
定义:一颗高度为n,且有 2ⁿ-1 个结点的二叉树
特点:
1、只有最后一层有叶子结点
2、不存在度为1的结点(只存在度为0或者2的结点)
3、按层序从1开始编号,结点 i 的左孩子为 2i,右孩子为 2i+1,结点 i 的父节点为 ⌊ i/2 ⌋;
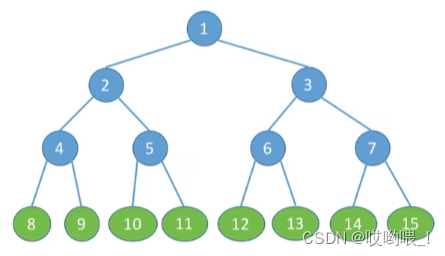
完全二叉树
定义:当且仅当其每个结点都与高度为 h 的满二叉树中的编号为 1~n 的结点一一对应时,称为完全二叉树
特点:
1、只有最后两层有叶子结点
2、最多只有一个度为1的结点
3、按层序从1开始编号,结点 i 的左孩子为 2i,右孩子为 2i+1,结点 i 的父节点为 ⌊ i/2 ⌋;(如果有的话)
4、i <= ⌊ n/2 ⌋ 为分支结点,i > ⌊ n/2 ⌋ 为叶子结点
如果某结点只有一个孩子,那么这个孩子一定是左孩子
二叉排序树
定义:一颗二叉树或者空二叉树具有如下性质的称为二叉排序树
1、左子树上所有结点的关键字均小于根结点的关键字
2、右子树上所有结点的关键字均大于根结点的关键字
3、左子树和右子树又各是一棵二叉排序树
二叉排序树可用于元素的排序和搜索
平衡二叉树
定义:树上任一结点的左子树和右子树的深度之差不超过1
平衡二叉树能有更高的搜索效率
二叉树的常考性质
考点一:设非空二叉树中度为0、1、2的结点个数分别为n0、n1、n2,则 n0 = n2 + 1; ( 叶子结点比二分支结点多一个 )
假设树中结点总数为n,则
① n = n0 + n1 +n2
② n = n1 + 2*n2 + 1 (树的结点数 = 总度数 + 1)
②-①得 n0 = n2 + 1
考点二:二叉树第 i 层至多有 2ⁱ⁻¹ 个结点(i>=1)
源于: m 叉树第 i 层至多有 mⁱ⁻¹ 个结点(i>=1)
考点三:高度为 n 的二叉树至多有 2ⁿ - 1 个结点(满二叉树)
源于: 高度为 n 的 m 叉树至多有 mⁿ - 1/m-1 个结点
完全二叉树的常考性质

常考考点2:对于完全二叉树,可以由结点数 n 推出度为0、1、2的结点个数为n0、n1、n2
完全二叉树最多只有一个度为1的结点,所以
n1 = 0或1
n0 = n2 + 1 ----> n0 + n2 = 2*n2 + 1 一定是奇数
若完全二叉树有 2k 个(偶数)个结点,则 n = n1 + n2 + n3,由上面得 n0 + n2 一定是奇数,所以只有 n1 = 1 时, n 才会是偶数
所以 n1 = 1,n0 = k,n2 = k-1
若完全二叉树有 2k-1 个(奇数)个结点,则 n = n1 + n2 + n3,由上面得 n0 + n2 一定是奇数,所以只有 n1 = 0 时, n 才会是奇数
所以 n1 = 0,n0 = k,n2 = k-1
二叉树的存储结构
顺序存储
定义一个长度为 MaxSize 的数组t,按照从上至下,从左至右的顺序依次存储完全二叉树中的各个结点
#define MaxSize 100
struct TreeNode{ElemType value; // 结点中的数据元素bool isEmpty; // 结点是否为空
}// 初始化时所有结点标记为空
for(int i = 0; i < MaxSize; i++){t[i].isEmpty = true;
}TreeNode t[MaxSize]
几个重要的常考的基本操作
i 的左孩子 ———— 2i
i 的右孩子 ———— 2i+1
i 的父节点 ———— ⌊ i/2 ⌋
i 所在的层次 ————
若完全二叉树中共有n个结点,则
判断 i 是否有左孩子? ———— 2i <= n
判断 i 是否有右孩子? ———— 2i+1 <= n
判断 i 是否是叶子/分支结点? ———— i > ⌊ n/2 ⌋
注意:如果不是完全二叉树,依然按照层序将各个结点顺序存储,那么无法从结点编号反映出以上这些逻辑关系,所以一定要把二叉树的结点编号与完全二叉树对应起来,但是会导致出现很多空值的存储单元
最坏情况:高度为 n 且只有 n 个结点的单支树(所有结点只有右孩子),也至少需要 2ⁿ - 1 个存储单元
结论:二叉树的顺序存储结构,只适合存储完全二叉树
链式存储
typedef struct BiTNode{ElemType data;struct BiTNode *lchild,*rchild; // 左右孩子指针
}BiTNode,*BiTree;
假设有n个结点,则有2n个指针域,除了根结点,每一个结点头上都会连接一个指针域,那么就有n-1个有值的指针域,得出就会有n+1个空指针域
n个结点的二叉链表共有n+1个空链域
根据实际需求决定要不要加父结点指针(三叉链表——方便找父结点)
typedef struct BiTNode{ElemType data;struct BiTNode *lchild,*rchild; // 左右孩子指针struct BiTNode *parent; // 父结点指针
}BiTNode,*BiTree;
二叉树的先中后序遍历
- 先序遍历:根左右
- 中序遍历:左根右
- 后序遍历:左右根
其中这三种遍历方式与前中后缀表达式的关系
先序遍历——>前缀表达式
中序遍历——>中缀表达式(需要加界限符)
后序遍历——>后缀表达式
先序遍历(空间复杂度:O(h))
void PreOrder(BiTree T){if(T!=NULL){visit(T); //访问根结点PreOrder(T->lchild); // 递归遍历左子树PreOrder(T->rchild); // 递归遍历右子树}
}
中序遍历
void PreOrder(BiTree T){if(T!=NULL){PreOrder(T->lchild); // 递归遍历左子树visit(T); //访问根结点PreOrder(T->rchild); // 递归遍历右子树}
}
后序遍历
void PreOrder(BiTree T){if(T!=NULL){PreOrder(T->lchild); // 递归遍历左子树PreOrder(T->rchild); // 递归遍历右子树visit(T); //访问根结点}
}
应用
求树的深度
int treeDepth(BiTree T){if(T == NULL)return 0;else{int l = treeDepth(T->lchild);int r = treeDepth(T->rchild);// 树的深度=Max(左子树深度,右子树深度) + 1return l>r ? l+1 : r+1;}
}
二叉树的层序遍历
算法思想:
①初始化一个辅助队列
②根结点入队
③若队列非空,则队头结点出队,访问该结点,并将其左、右孩子插入队尾(如果有的话)
④重复③直至队列为空
// 二叉树的结点(链式存储)
typedef struct BiTNode{char data;struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;// 链式队列结点
typedef struct LinkNode{BiTNode *data; // 存指针,而不是结点struct LinkNode *next;
}LinkNode;typedef struct{LinkNode *front,*rear; // 队头队尾
}LinkQueue;// 层序遍历
void LevelOrder(BiTree T){LinkQueue(Q);InitQueue(Q); // 初始化辅助队列BiTree p;EnQueue(Q,T); // 将根结点入队while(!IsEmpty(Q)){DeQueue(Q,p); // 队头结点出队visit(p); // 访问出队结点if(p->lchild!=NULL)EnQueue(Q,(p->lchild); // 左孩子入队if(p->rchild!=NULL)EnQueue(Q,(p->rchild); // 右孩子入队}
}
由遍历序列构造二叉树
若只给出一颗二叉树的前中后序遍历序列中的一种,不能唯一确定一棵二叉树
能构造二叉树的遍历序列组合
1、前序+中序
2、后序+中序
3、层序+中序
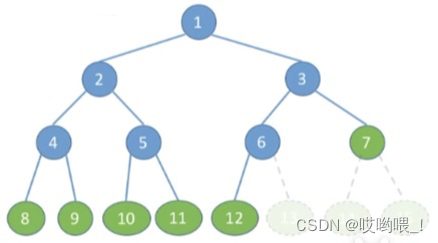
线索二叉树
问题1:如何找到指定结点在中序遍历序列中的前驱?
问题2:如何找到结点的中序后继?
找前驱和后继很不方便,遍历操作必须从根开始
还记得之前学到的,n个结点的二叉树,有n+1个空链域,可以用来记录前驱、后继的信息
线索二叉树的存储结构
typedef struct ThreadNode{ElemType data;struct ThreadNode *lchild,*rchild;int ltag,rtag; // 左右线索标志
}ThreadNode,*ThreadTree;
// tag=0 表示指针指向孩子
// tag=1 表示指针是线索

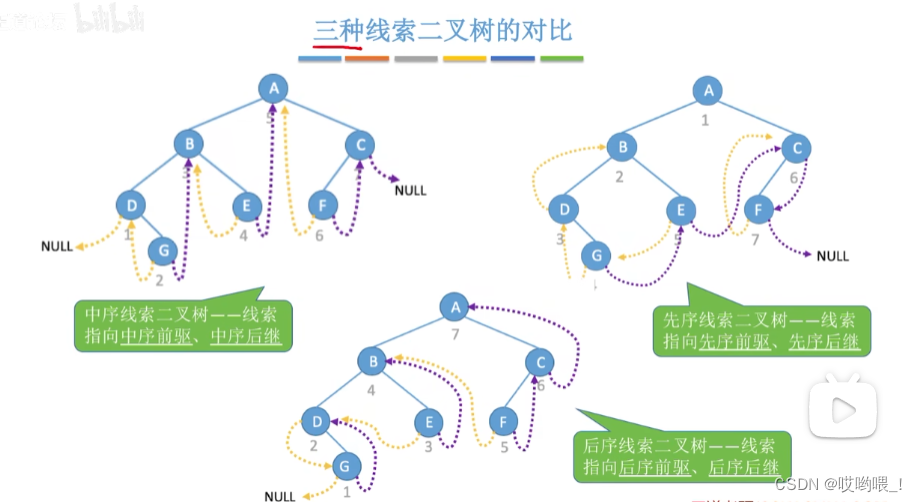
二叉树的线索化
中序线索化
// 线索二叉树结点
typedef struct ThreadNode{ElemType data;struct ThreadNode *lchild,*rchild;int ltag,rtag; // 左右线索标志
}ThreadNode,*ThreadTree;void visit(ThreadNode *q){if(q->lchild==NULL){ //左子树为空,建立前驱线索q->lchild=pre;q->ltag=1;}if(pre!=NULL&&pre->rchild==NULL){ //前驱结点的右孩子为空,建立前驱结点的后驱线索pre->rchild=q;pre->rtag=1;}pre=q;
}//中序遍历二叉树,一边遍历一边线索化
void InThread(ThreadTree T){if(T!=NULL){InThread(T->lchild); // 中序遍历左子树visit(T); // 访问根结点InThread(T->rchild); // 中序遍历右子树}
}// 全局变量 pre,指向当前访问结点的前驱
ThreadNode *pre=NULL;// 中序线索化二叉树T
void CreateInThread(ThreadTree T){pre=NULL; // pre初始化为NULLif(T!=NULL){InThread(T) //中序线索化二叉树if(pre->rchild==NULL)pre->rtag=1; // 处理遍历的最后一个点}
}
先序线索化(与中序遍历有一点不一样:为了防止重复指向,需要判断lchild不是前驱线索)
// 线索二叉树结点
typedef struct ThreadNode{ElemType data;struct ThreadNode *lchild,*rchild;int ltag,rtag; // 左右线索标志
}ThreadNode,*ThreadTree;void visit(ThreadNode *q){if(q->lchild==NULL){ //左子树为空,建立前驱线索q->lchild=pre;q->ltag=1;}if(pre!=NULL&&pre->rchild==NULL){ //前驱结点的右孩子为空,建立前驱结点的后驱线索pre->rchild=q;pre->rtag=1;}pre=q;
}//先序遍历二叉树,一边遍历一边线索化
void PreThread(ThreadTree T){if(T!=NULL){visit(T); // 访问根结点if(T->ltag==0){ // 与中序遍历不一样的地方,为了防止重复指向,需要判断lchild不是前驱线索PreThread(T->lchild); // 与中序遍历不一样的地方,为了防止重复指向,需要判断lchild不是前驱线索PreThread(T->rchild);}
}// 全局变量 pre,指向当前访问结点的前驱
ThreadNode *pre=NULL;// 先序线索化二叉树T
void CreateInThread(ThreadTree T){pre=NULL; // pre初始化为NULLif(T!=NULL){InThread(T) //先序线索化二叉树if(pre->rchild==NULL)pre->rtag=1; // 处理遍历的最后一个点}
}
后序线索化(和中序差不多)
// 线索二叉树结点
typedef struct ThreadNode{ElemType data;struct ThreadNode *lchild,*rchild;int ltag,rtag; // 左右线索标志
}ThreadNode,*ThreadTree;void visit(ThreadNode *q){if(q->lchild==NULL){ //左子树为空,建立前驱线索q->lchild=pre;q->ltag=1;}if(pre!=NULL&&pre->rchild==NULL){ //前驱结点的右孩子为空,建立前驱结点的后驱线索pre->rchild=q;pre->rtag=1;}pre=q;
}//后序遍历二叉树,一边遍历一边线索化
void InThread(ThreadTree T){if(T!=NULL){InThread(T->lchild); // 后序遍历左子树InThread(T->rchild); // 后序遍历右子树visit(T); // 访问根结点}
}// 全局变量 pre,指向当前访问结点的前驱
ThreadNode *pre=NULL;// 后序线索化二叉树T
void CreateInThread(ThreadTree T){pre=NULL; // pre初始化为NULLif(T!=NULL){InThread(T) //后序线索化二叉树if(pre->rchild==NULL)pre->rtag=1; // 处理遍历的最后一个点}
}
二叉树的线索化
中序线索二叉树中找到指定结点*p的中序后继next
① 若 p->rtag=1, 则 next = p->rchild
② 若 p->rtag=0, 则 next = p的右子树中最左下结点
// 找到以p为根的子树中,第一个被中序遍历的结点
ThreadNode *Firstnode(ThreadNode *p){// 循环找到最左下结点(不一定是叶结点)while(p->ltag==0) p=p->lchild;return p;
}// 在中序线索二叉树中找到结点p的后继结点
ThreadNode *Nextnode(ThreadNode *p){// 右子树下最左的结点if(p->rtag==0) return Firstnode(p->rchild);esle return p->rchild; // rtag ==1 直接返回后继线索
}// 对中序线索二叉树进行中序遍历(利用线索实现的非递归算法)空间复杂O(1)
void Inorder(TreadNode *T){for(ThreadNode *p=Firstnode(T);p!=NULL;p=Nextnode(p)){visit(p);}
}
中序线索二叉树中找到指定结点*p的中序前驱pre
① 若 p->ltag=1, 则 pre= p->rchild
② 若 p->rlag=0, 则 pre= p的左子树中最右下结点
// 找到以p为根的子树中,最后一个被中序遍历的结点
ThreadNode *Lastnode(ThreadNode *p){// 循环找到最左下结点(不一定是叶结点)while(p->rtag==0) p=p->rchild;return p;
}// 在中序线索二叉树中找到结点p的前驱结点
ThreadNode *Prenode(ThreadNode *p){// 左子树中最右下结点if(p->ltag==0) return Lastnode(p->lchild);esle return p->lchild; // ltag ==1 直接返回前驱线索
}// 对中序线索二叉树进行逆向中序遍历
void RevInorder(TreadNode *T){for(ThreadNode *p=Lastnode(T);p!=NULL;p=Prenode(p)){visit(p);}
}
在先序线索二叉树中找到指定结点*p的先序后继next
① 若 p->rtag=1, 则 next = p->rchild
② 若 p->rtag=0,
1、若p有左孩子,则先序后继为左孩子
2、若p没有左孩子,则先序后继为右孩子
在先序线索二叉树中找到指定结点*p的先序前驱pre
① 若 p->ltag=1, 则 next = p->lchild
② 若 p->ltag=0, 需要从头开始遍历
在后序线索二叉树中找到指定结点*p的后序前驱pre
① 若 p->ltag=1, 则 pre= p->lchild
② 若 p->ltag=0,
1、若p有右孩子,则后序前驱为右孩子
2、若p没有右孩子,则后序前驱为左孩子
在后序线索二叉树中找到指定结点*p的后序后继next
① 若 p->rtag=1, 则 next = p->rchild
② 若 p->rtag=0, 需要从头开始遍历
相关文章:

数据结构详细笔记——二叉树
文章目录 二叉树的定义和基本术语特殊的二叉树满二叉树完全二叉树二叉排序树平衡二叉树 二叉树的常考性质完全二叉树的常考性质二叉树的存储结构顺序存储链式存储 二叉树的先中后序遍历先序遍历(空间复杂度:O(h))中序遍…...
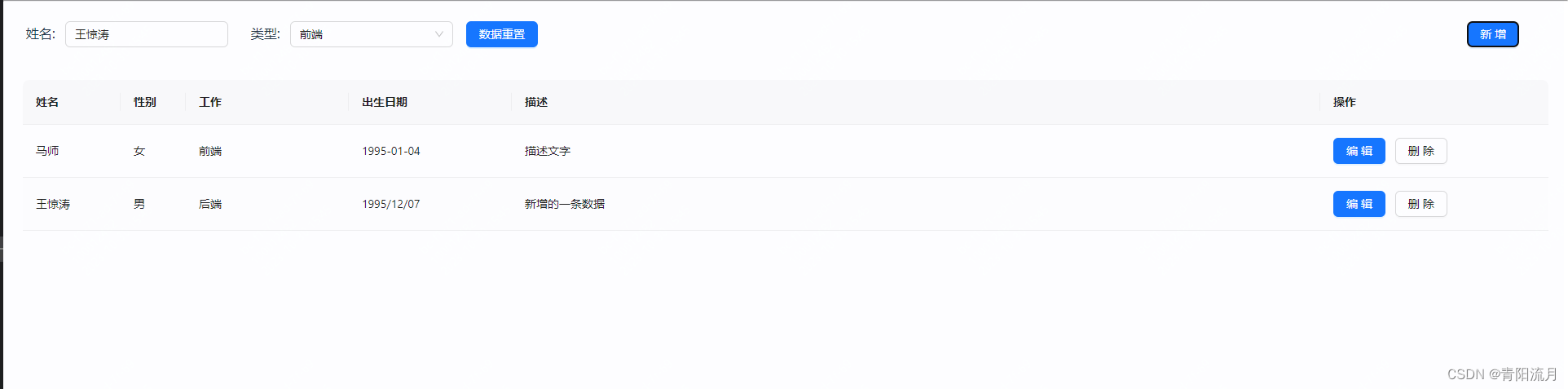
react实现列表增删改查的小demo(class组件版)
前言 react的语法上就是比vue麻烦不少,既然要开手动挡,那就开吧,一个基础的demo 效果图 列表 新增弹窗 编辑弹框 新增一条数据后的效果 代码 根组件 index.jsx import React, { Component,createRef} from react import withRouter from ../../utils/withRouter import G…...
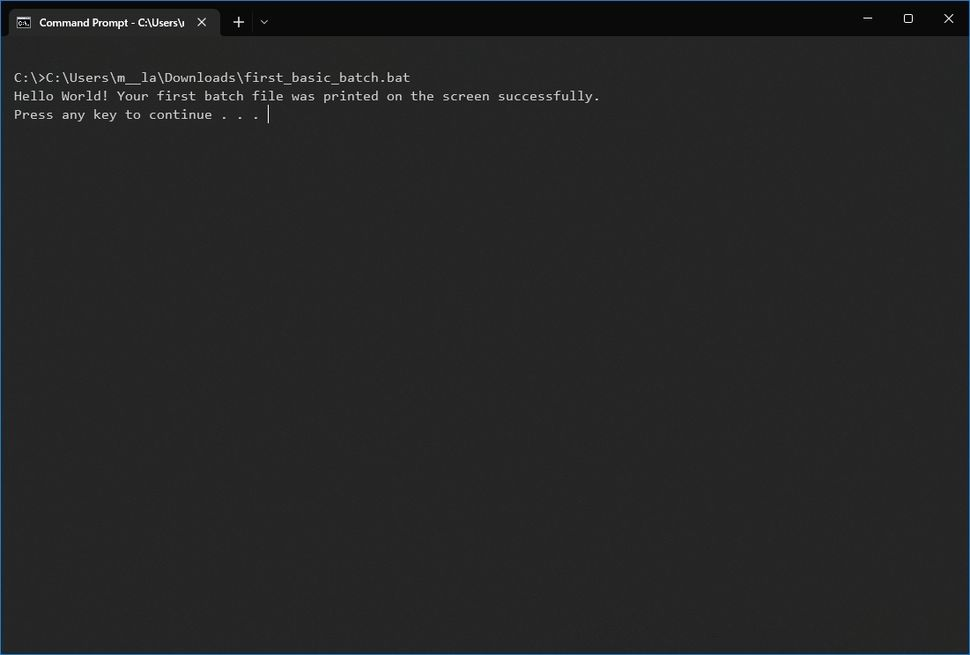
运行批处理文件,Windows 10至少提供了三种方法,有的可以设置定时运行
Windows 10至少有三种写入批处理文件的方法。你可以使用命令提示符或文件资源管理器按需运行它们。你可以使用任务计划程序配置脚本,以便按计划运行。或者,你可以将批处理文件保存在“启动”文件夹中,让系统在你登录帐户后立即运行它们。 如果要按需运行脚本,可以使用文件…...

C++ detach线程的归属权和控制权交给runtime library的原因
在C中,std::thread的detach操作将线程的归属权和控制权都转移给了C运行时库(runtime library)。这是因为detach操作的目的是告诉C运行时库,你不再关心这个线程的状态,它可以在后台独立运行,而不需要等待主线…...
Android应用集成RabbitMQ消息处理指南
Android应用集成RabbitMQ消息处理指南 RabbitMQ1、前言2、RabbitMQ简介2.1、什么是RabbitMQ2.2、RabbitMQ的特点2.3、RabbitMQ的工作原理2.4、RabbitMQ中几个重要的概念 3、在Android Studio中集成RabbitMQ3.1、在Manifest中添加权限:3.2、在build.gradle(:app)下添…...

爆改86㎡户型,中式禅意,自然诗意!福州中宅装饰,福州装修
自然诗意 中式禅意 东方风韵,涟漪泛晕。 ——致生活感的“空间”,最美的家 案例简介 作品:泛晕 风格:新中式 面积:86平方 楼盘:长乐中南樾府 中国风与现代风混搭 木元素是中国风表达中最具灵魂般的存…...
LVGL库入门 02 - 布局
1、简单布局 可以使用 lv_obj_set_pos(obj, x, y) 调整一个控件的位置(或者使用类似的函数单独调整一个方向的坐标),将它放在相对父容器左上角的合适位置。不过这种布局方式非常死板,因为绝对坐标一旦设定就不能自动调整…...
利用Vue2实现印章徽章组件
需要实现的组件效果: 该组件有设置颜色、大小、旋转度数和文本内容功能。 一、组件实现代码 <template><divclass"first-ring"v-bind"getBindValue":class"getStampBadgeClass":style"{ transform: rotate(${rotate}…...

金麟国际用工-全新蓝领跨境就业服务平台
金麟国际用工-全新蓝领跨境就业服务平台 金麟国际用工平台是一个引领时代的蓝领跨境就业服务平台,专为蓝领求职者和雇主提供一个全面、便捷、高效的就业对接环境。这个平台通过其强大的数字化系统,包括客户管理系统、岗位信息系统和智能营销工具等&…...

性能测试知多少---并发用户
在做性能测试的时候,我们常常听到并发用户、响应时间、吞吐量专业术语,也许大家都理解,这里有一个理解的层次与深度概念。最近有看断念《软件性能详解与案例分析》一书,看了他的讲解,原来我对这些术语的理解还是比较肤…...
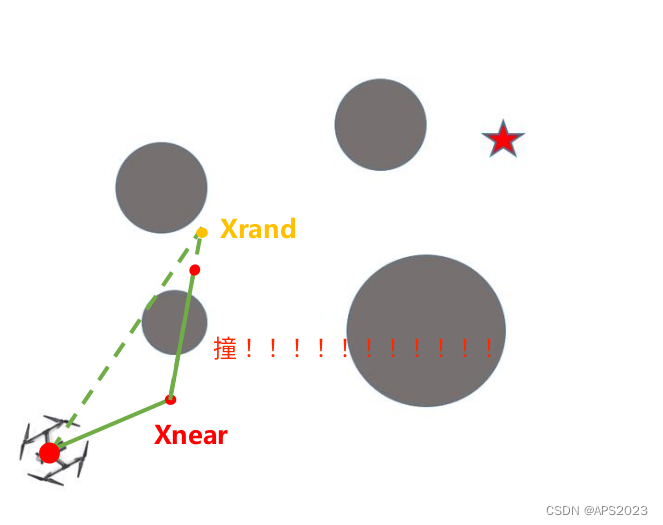
自动驾驶算法(三):RRT算法讲解与代码实现(基于采样的路径规划)
目录 1 RRT算法原理 2 RRT算法代码解析 3 RRT完整代码 1 RRT算法原理 RRT算法的全称是快速扩展随机树算法(Rapidly Exploring Random Tree),它的想法就是从根结点长出一棵树当树枝长到终点的时候这样就能找到从终点到根节点的唯一路径。 算法流程: 首先…...
基于SSM的酒店客房预定管理系统
基于SSM的酒店客房预定管理系统的设计与实现~ 开发语言:Java数据库:MySQL技术:SpringSpringMVCMyBatis工具:IDEA/Ecilpse、Navicat、Maven 系统展示 前台主页 客房详情 登录界面 管理员界面 用户界面 摘要 基于SSM(…...
IDEA初步入门
1 安装 现在的系统更迭很快,很多软件都只支持win10 和 11了,但我们过时党还在用win7. 所以就必须找到合适的版本。在windows 7 64位系统下,可以使用IDEA 2020.1.4版本。 在Jetbrain官方下,找到历史版本,找到windows版…...

《Webpack 5 基础配置》- 禁止在出现编译错误或警告时,覆盖浏览器全屏显示
Webpack5 overlay 配置地址默认编译错误或警告为 true,即浏览器全屏显示;overlay 属性可以是 boolean 型,也可是 object 类型;还有其它设置说明,详见上述官网地址; module.exports {devServer: {client: {…...

echart 饼图怎么让图形铺满整个div
1.原效果(未铺满):原配置 2.如果想要铺满,需要设置radius ,radius的意思是 第一个元素为内环半径,第二个参数为外环半径; 如果想要填满的话直接写[0,100%],不过第一个为0后就不是圆环里&#…...

回归预测 | Matlab实现WOA-CNN-SVM鲸鱼算法优化卷积神经网络-支持向量机的多输入单输出回归预测
回归预测 | Matlab实现WOA-CNN-SVM鲸鱼算法优化卷积神经网络-支持向量机的多输入单输出回归预测 目录 回归预测 | Matlab实现WOA-CNN-SVM鲸鱼算法优化卷积神经网络-支持向量机的多输入单输出回归预测效果一览基本介绍程序设计参考资料 效果一览 基本介绍 1.WOA-CNN-SVM鲸鱼算法…...

arm-none-eabi-gcc下实现printf的两种方式
方式1,移植第三方printf库: 1. 下载地址:https://github.com/mpaland/printf 2. 拷贝其中的printf.c和printf.h到本地; 3. 重新实现 void _putchar(char character) 接口,使用具体串口发送ch数据,如在 u…...

组件库开发
组件库开发 环境搭建 menorepo pnpmpnpm-workspacelerna 7.4.2 (已全局安装lerna) 1、初始化 1.1 新建项目目录root 1.2 在目录root中使用pnpm初始化packages.json文件,新建 pnpm-workspace.yaml文件, packages/文件夹 pnp…...

【python基础】魔法参数*args, **kwargs的使用
文章目录 前言一、*args 和 **kwargs 是什么?二、*args 的用法打包参数:将不定数量的参数传递给一个函数拆分参数:调用一个函数 三、**kwargs 的用法打包参数:将不定数量的参数传递给一个函数拆分参数:调用一个函数 四…...

Android Icon 添加水印 Python脚本
源代码 # -*- coding: utf-8 -*- from PIL import Image 图片合成def mergePictureLXJ():commonIcon Image.open("icon.png")markIcon Image.open("领现金.png")markLayer Image.new(RGBA, commonIcon.size, (0, 0, 0, 0))markLayer.paste(markIcon, (0…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...