微型计算机组成原理
1、微型计算机组成
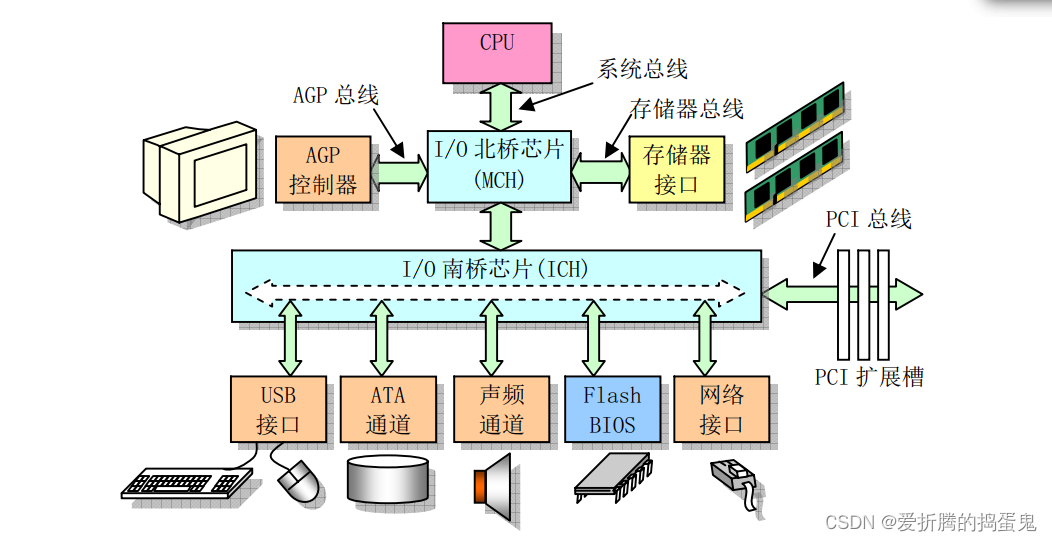
一个传统微型计算机硬件组成如下图

CPU通过地址线、数据线和控制信号线组成的本地总线(内部总线)与系统其他部分进行数据通信。
- 地址线用于提供内存或I/O设备的地址,即指明需要读/写数据的具体位置;
- 数据线用于在CPU和内存或I/O设备之间提供数据传输的通道;
- 控制线负责指挥执行的具体读/写操作。
对于80386CPU来说,其内部地址线和数据线都是32根,即32位,因此地址空间范围为2^32字节,从0~4GB。
现代PC机主板主要通过2个超大规模芯片构成的芯片组或芯片集组成:北桥(Northbridge)芯片和南桥(Southbridge)芯片。
- 北桥芯片用于与CPU、内存和AGP视频接口,这些接口具有很高的传输速率,北桥芯片和可以起存储器控制作用,因此Intel把该芯片标号为MCH(Memory Controller Hub);
- 南桥芯片用来管理低、中速的组件,例如:PCI总线,IDE硬盘接口、USB端口等,因此南桥芯片被称为ICH(I/O Controller Hub)。
2、I/O端口寻址和访问控制方式
CPU通过I/O端口地址来访问I/O接口控制器或控制卡上的数据和状态信息。通常一个I/O控制器包含访问数据的数据端口、输出命令的命令端口和访问控制器执行状态的状态端口。端口地址的设置方法一般有两种:统一编址和独立编址。
- 统一编址的原理:把I/O控制器中的端口地址归入存储器寻址地址空间范围内。CPU访问一个端口的操作与访问内存的操作一样,也使用访问内存的指令。
- 独立编址的原理:把I/O控制器和控制卡的的寻址空间单独作为一个独立的地址空间对待,称为I/O地址空间。每个端口有一个I/O地址与之对应,并且使用专门的I/O指令来访问端口。
PC机I/O接口数据传输控制方式一般可采用程序循环查询方式、中断处理方式和DMA传输方式。
- 循环查询方式是指CPU通过在程序中循环查询指定设备控制器中的状态来判断是否可以与设备进行数据交换。这种方式不需要过多的硬件支持,使用和编程都比较简单,但是特别耗费CPU时间。
- 中断处理控制方式需要中断控制器的支持,当I/O设备通过中断向CPU提出处理请求时,CPU会暂时中断当前执行的程序转而执行相应的I/O中断处理服务过程。当执行完成后,CPU又会继续执行刚才被中断的程序。在I/O控制器或设备发出中断请求时,CPU通过使用中断向量表(中断描述符表)来寻址相应的中断处理服务过程的入口地址。因此采用中断控制方式时需要首先设置好中断向量表,并编制好相应的中断处理服务过程。
- 直接存储器访问DMA(Direct Memory Access)方式用于I/O设备与系统内存之间进行批量数据传输,整个过程需要使用专门的DMA控制器来进行而无需CPU插手。
串行通信是指在线路上以比特位数据流一次一个比特进行传输的通信方式。串行通信可分为异步和同步串行通信两种。
- 异步串行通信以一个字符作为通信单位或一帧进行传输;
- 同步串行通信以多个字符或字节组成的序列作为一帧数据进行传输。
相关文章:

微型计算机组成原理
1、微型计算机组成 一个传统微型计算机硬件组成如下图 CPU通过地址线、数据线和控制信号线组成的本地总线(内部总线)与系统其他部分进行数据通信。 地址线用于提供内存或I/O设备的地址,即指明需要读/写数据的具体位置;数据线用…...
基站/手机是怎么知道信道情况的?
在无线通信系统中,信道的情况对信号的发送起到至关重要的作用,基站和手机根据信道的情况选择合适的资源配置和发送方式进行通信,那么基站或者手机是怎么知道信道的情况呢? 我们先来看生活中的一个例子,从A地发货到B地…...

进程/线程
进程是资源单位, 线程是执行单位。 每一个进程至少要有一个线程,启动每一个程序默认都会有一个主线程 1.多线程的两种实现 from threading import Thread#方法一 def func(name):for i in range(10):print(name, i)if __name__ __main__:t Thread(targetfunc, …...
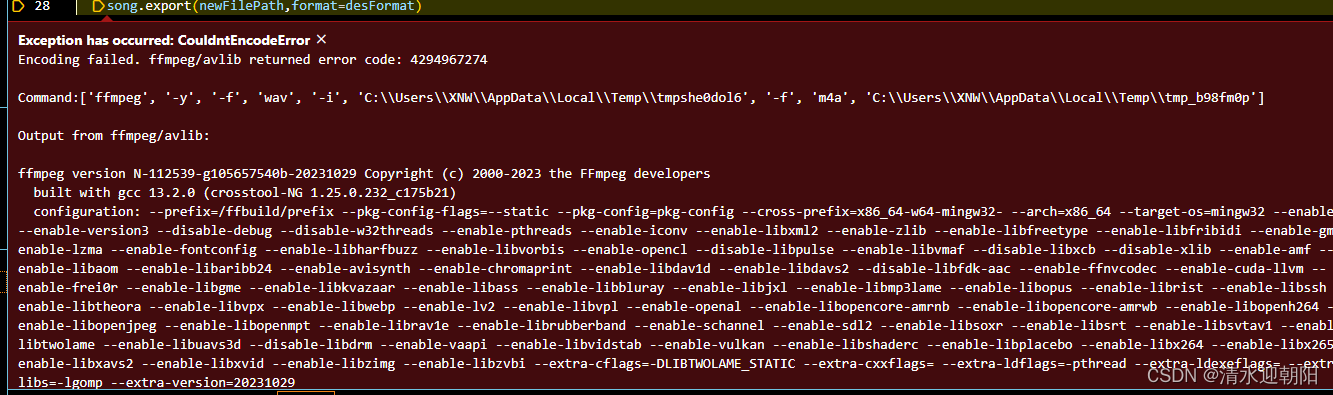
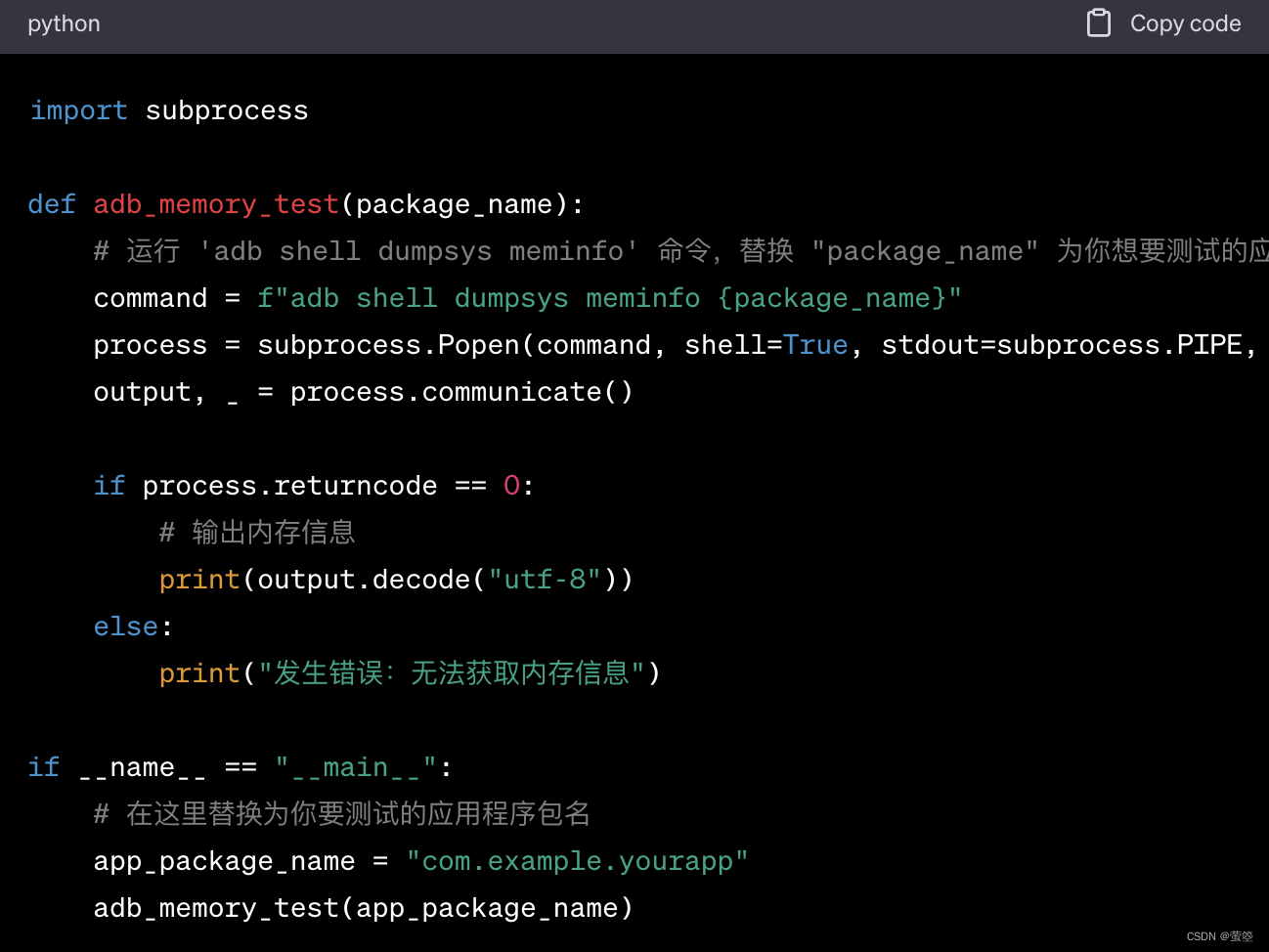
Python 应用 之 转换音频格式
目录 一、python音频转换 1、pydub 音频包安装 2、 ffmpeg安装 1)、解压后,添加到环境变量中 2)、可以直接放在python安装目录下 3、python程序 1)、引入相关包 2)、重命名 3)、to Mp3 4…...

Oracle JDK 和OpenJDK两者有什么异同点
Oracle JDK 和 OpenJDK 是两种不同版本的 Java Development Kit(Java 开发工具包),它们都提供了用于开发 Java 程序的一系列工具和库。以下是它们之间的一些主要异同点: 相同点: 功能:在大多数情况下&…...
GPT引发智能AI时代潮流
最近GPT概念爆火,许多行业开始竞相发展AI ,工作就业也将面临跳转,目前测试就业形势就分为了两大类,一类是测试行业如功能、性能、自动化综合性人才就业技能需求,另一类便是AI测试行业的需求普遍增长,原本由…...

FreeSWITCH mrcp-v2小记
最近得知有人受mrcp的困扰,于是写了这篇小文,希望能有所帮助 FreeSWITCH版本选择 目前当然选择1.10.10,不建议老版本,差别在于老版本用到的libmrcp比较旧,是1.2版本,bug比较多,有时会crash&am…...
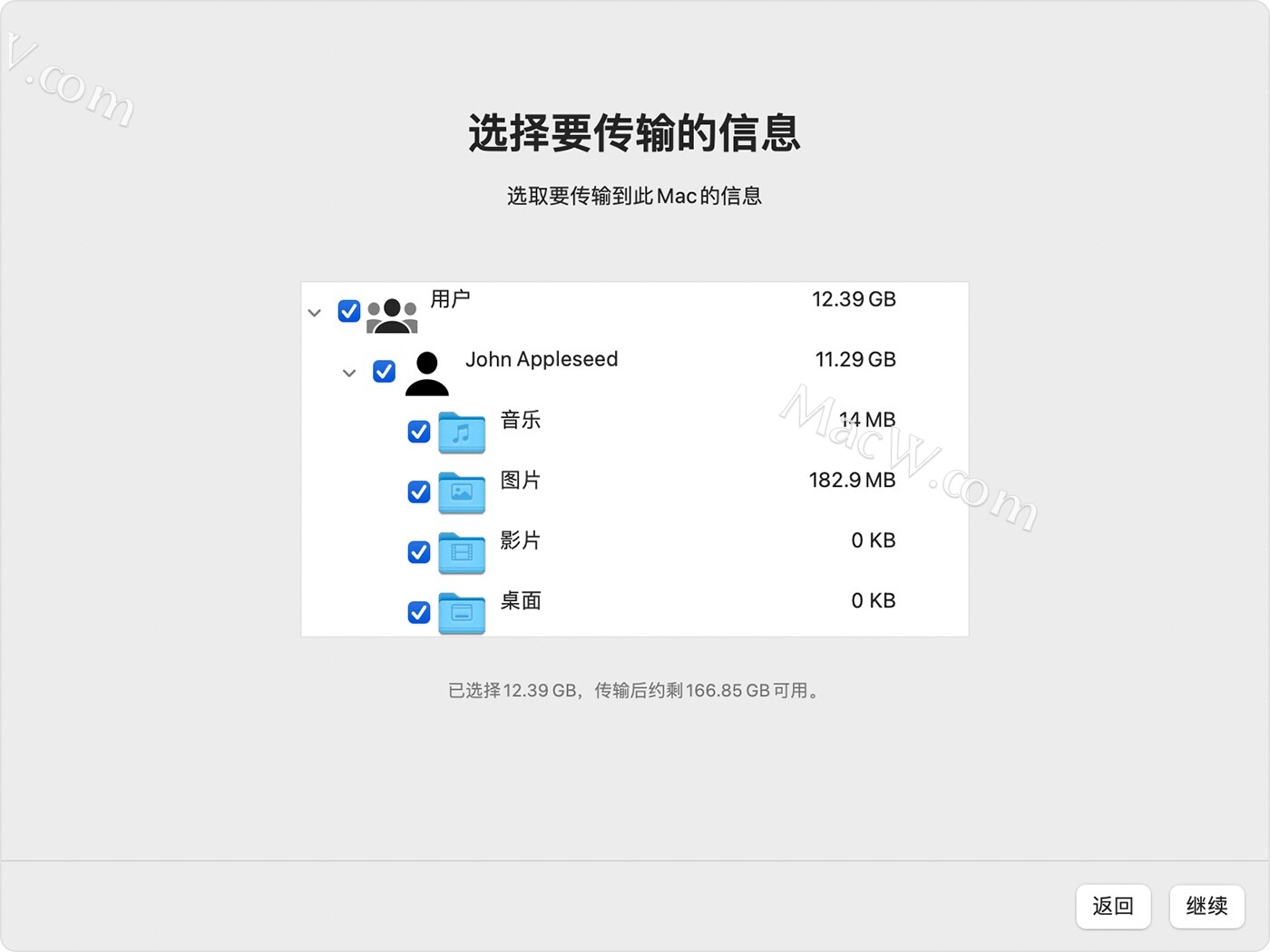
如何将你的PC电脑数据迁移到Mac电脑?使用“迁移助理”从 PC 传输到 Mac的具体操作教程
有的小伙伴因为某一项工作或者其它原因由Windows电脑换成了Mac电脑,但是数据和文件都在原先的Windows电脑上,不知道怎么传输。接下来小编就为大家介绍使用“迁移助理”将你的通讯录、日历、电子邮件帐户等内容从 Windows PC 传输到 Mac 上的相应位置。 在…...

Elasticsearch集群搭建、数据分片以及位置坐标实现附近的人搜索
集群搭建、数据分片 es使用两种不同的方式来发现对方: 广播单播也可以同时使用两者,但默认的广播,单播需要已知节点列表来完成 一 广播方式 当es实例启动的时候,它发送了广播的ping请求到地址224.2.2.4:54328。而其他的es实例使用同样的集群名称响应了这个请求。 一般这…...

深度学习_3 数据操作之线代,微分
线代基础 标量 只有一个元素的张量。可以通过 x torch.tensor(3.0) 方式创建。 向量 由多个标量组成的列表(一维张量)。比如 x torch.arange(4) 就是创建了一个1*4的向量。可以通过下标获取特定元素(x[3]),可以通…...
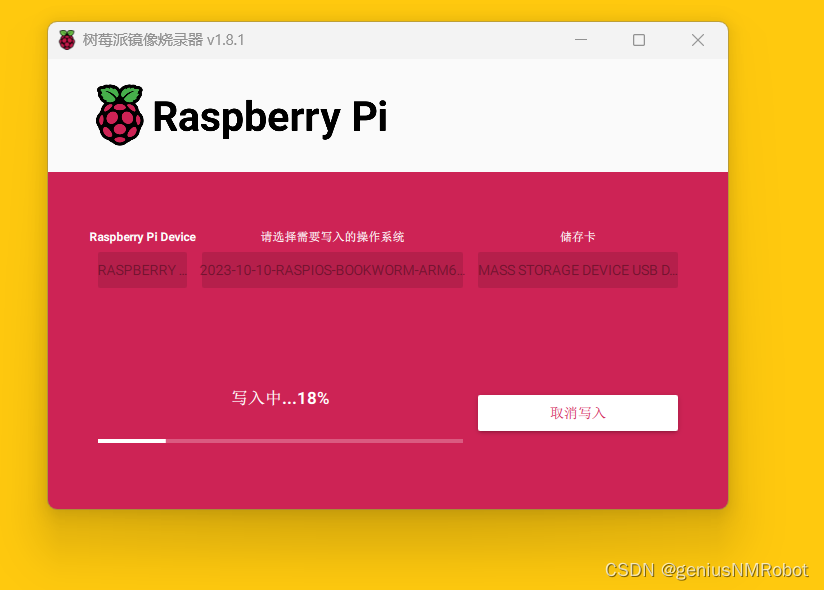
树莓派安装Ubuntu22.04LTS桌面版
工具:树莓派4B Raspberry Pi 自己下载的ubuntu22.04LTS img磁盘镜像文件 这里有一个小技巧:这个Raspberry Pi的选择镜像的时候在最后面一行可以选择自定义的镜像,哈哈哈哈,这就使得我们可以自己下载,而且知道那个文…...
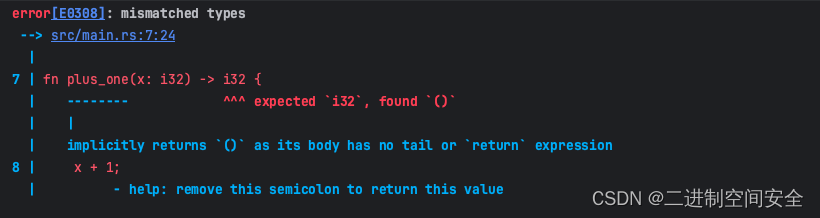
Rust编程基础之函数和表达式
1.Rust函数 在之前的文章中,我们已经见到了一个函数:main函数, 它是很多程序的入口点。也见过 fn 关键字,它用来声明新函数。 Rust 代码中的函数和变量名使用 snake case 规范风格。在 snake case 中,所有字母都是小写并使用下划线分隔单词。这是一个包…...

关于preempt count的疑问
Linux中的preempt_count - 知乎 https://www.cnblogs.com/hellokitty2/p/15652312.html LWN:关于preempt_count()的四个小讨论!-CSDN博客 主要是参考这些文章 之前一直认为只要是in_interrupt()返回非0值,那么就可以认为当前在中断上下文。即…...

Windows 开启 Kerberos 的火狐 Firefox 浏览器访问yarn、hdfs
背景:类型为IPA或者MIT KDC,windows目前只支持 firefoxMIT Kerberos客户端的形式,其他windows端浏览器IE、chrome、edge,没有办法去调用MIT Kerberos Windows客户端的GSSAPI验证方式,所以均无法使用 Windows 开启 Kerb…...
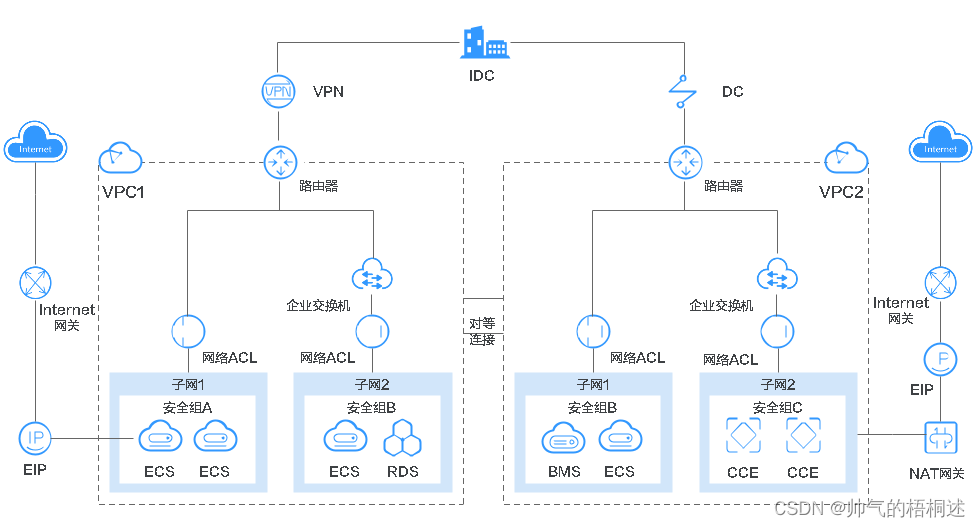
华为云资源搭建过程
网络搭建 EIP: 弹性EIP,支持IPv4和IPv6。 弹性公网IP(Elastic IP)提供独立的公网IP资源,包括公网IP地址与公网出口带宽服务。可以与弹性云服务器、裸金属服务器、虚拟IP、弹性负载均衡、NAT网关等资源灵活地绑定及解绑…...

突破防火墙的一种方法
当Linux防火墙阻止来自某个ip的数据时,它应该是根据ip数据报里“源IP地址”字段取得的对方ip吧,那对方就不能通过篡改“源IP地址”来绕过防火墙吗?NAT模式下的路由器就修改了这个字段。 但这样的话,攻击者是收不到服务器返回的数…...
Docker 多阶段构建的原理及构建过程展示
Docker多阶段构建是一个优秀的技术,可以显著减少 Docker 镜像的大小,从而加快镜像的构建速度,并减少镜像的传输时间和存储空间。本文将详细介绍 Docker 多阶段构建的原理、用途以及示例。 Docker 多阶段构建的原理 在传统的 Docker 镜像构建…...

【开题报告】基于Spring Boot的家装产品展示交易平台的设计与实现
1.研究背景和目的 随着人们对居住环境舒适度和个性化需求的不断提升,家装市场正逐渐发展成为一个重要的消费领域。为了满足消费者对家装产品的需求,建立一个高效、可靠的家装产品展示交易平台变得尤为重要。本项目旨在通过使用Spring Boot框架ÿ…...

MacOS安装git
文章目录 通过Xcode Command Lines Tool安装(推荐)终端直接运行git命令根据流程安装先安装Command Lines Tool后再安装git 官网下载二进制文件进行安装官方国外源下载二进制文件(不推荐)国内镜像下载二进制文件(推荐)安装git 通过Xcode Command Lines Tool安装(推荐) 简单来讲C…...
京东协议算法最新版
环境准备 1 com.jingdong.app.mall11.6.4 入口定位 逆向分析,发现 params 里面有一个 sign 以及请求头里面有一个 jdgs 首先我们发现京东的 sign 是 32 位的,猜测其可能是 md5 之类的 hash 算法,既然是 hash 算法,那么就大概率…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...
