C++二分查找算法的应用:俄罗斯套娃信封问题
本文涉及的基础知识点
二分查找
题目
给你一个二维整数数组 envelopes ,其中 envelopes[i] = [wi, hi] ,表示第 i 个信封的宽度和高度。
当另一个信封的宽度和高度都比这个信封大的时候,这个信封就可以放进另一个信封里,如同俄罗斯套娃一样。
请计算 最多能有多少个 信封能组成一组“俄罗斯套娃”信封(即可以把一个信封放到另一个信封里面)。
注意:不允许旋转信封。
示例 1:
输入:envelopes = [[5,4],[6,4],[6,7],[2,3]]
输出:3
解释:最多信封的个数为 3, 组合为: [2,3] => [5,4] => [6,7]。
示例 2:
输入:envelopes = [[1,1],[1,1],[1,1]]
输出:1
参数提示:
1 <= envelopes.length <= 105
envelopes[i].length == 2
1 <= wi, hi <= 105
超时解法
有两个地方可能超时:
一,std::map<int, int> dp = mPreYToNum;
二,for (; (ij != dp.end()) && (ij->second > len); ++ij);
一处的时间复杂度是:O(n),最多有n个元素,所以总时间复杂度是O(n*n),会引起超时。
二处,总时间复杂度是O(n),最多删除n次,每个元素最多只会被删除一次。
代码
class Solution {
public:
int maxEnvelopes(vector<vector>& envelopes) {
std::map<int, vector> mXToYS;
for (const auto& v : envelopes)
{
mXToYS[v[0]].emplace_back(v[1]);
}
std::map<int, int> mPreYToNum;//y值对应最大数量,y值越大,对应的数量越大,否则被淘汰了
int iMax = 0;
for (const auto& it : mXToYS)
{
std::map<int, int> dp = mPreYToNum;
for (const auto& y : it.second)
{
int len = 0;
{//计算长度
const auto it = mPreYToNum.lower_bound(y);
len = 1 + ((mPreYToNum.begin() == it) ? 0 : std::prev(it)->second);
iMax = max(iMax, len);
}
{
const auto it = dp.lower_bound(y);
auto ij = it;
for (; (ij != dp.end()) && (ij->second > len); ++ij);
dp.erase(it, ij);
if (!dp.count(y))
{
dp[y] = len;
}
}
}
mPreYToNum.swap(dp);
}
return iMax;
}
};
测试用例
template
void Assert(const T& t1, const T& t2)
{
assert(t1 == t2);
}
template
void Assert(const vector& v1, const vector& v2)
{
if (v1.size() != v2.size())
{
assert(false);
return;
}
for (int i = 0; i < v1.size(); i++)
{
Assert(v1[i] ,v2[i]);
}
}
int main()
{
Solution slu;
vector<vector> envelopes;
int res = 0;
envelopes = { {5,4},{6,4},{6,7},{2,3} };
res = slu.maxEnvelopes(envelopes);
Assert(res, 3);
envelopes = { {1,1},{1,1},{1,1} };
res = slu.maxEnvelopes(envelopes);
Assert(res, 1);
envelopes = { {1,1},{2,2},{2,3} };
res = slu.maxEnvelopes(envelopes);
Assert(res, 2);
envelopes = { {1,2},{2,3},{3,4},{3,5},{4,5},{5,5},{5,6},{6,7},{7,8} };
res = slu.maxEnvelopes(envelopes);
Assert(res, 7);
//CConsole::Out(res);
}
正确解法
变量含义
| mXToYS | key为envelopes的x,值为envelopes的y |
| mYToNum | [x取[0,x), y对应最大套娃数量 |
| vector<pair<int, int>> vYNum | 当前x,各y对应数量 |
注意:
x相同,无法套娃,所以必须等当前x处理完毕,才能更新mYToNum。
y值越大,对应的数量越大,否则被淘汰了。所以mYToNum的键和值都是升序。
y小于当前y的,不会淘汰当前y,因为当前长度就是小于y的最大长度+1。
所以只会被相等的y淘汰。
当前y 可能淘汰比当前y大的。
代码
class Solution {
public:
int maxEnvelopes(vector<vector>& envelopes) {
std::map<int, vector> mXToYS;
for (const auto& v : envelopes)
{
mXToYS[v[0]].emplace_back(v[1]);
}
std::map<int, int> mYToNum;//y值对应最大数量
int iMax = 0;
for (const auto& it : mXToYS)
{
vector<pair<int, int>> vYNum;
for (const auto& y : it.second)
{
const auto it = mYToNum.lower_bound(y);
const int num = 1 + ((mYToNum.begin() == it) ? 0 : std::prev(it)->second);
iMax = max(iMax, num);
vYNum.emplace_back(y, num);
}
for(const auto[y,num]: vYNum)
{
const auto it = mYToNum.lower_bound(y);
auto ij = it;
for (; (ij != mYToNum.end()) && (ij->second <= num); ++ij);
mYToNum.erase(it, ij);
if (!mYToNum.count(y))
{
mYToNum[y] = num;
}
}
}
return iMax;
}
};
2023年1月旧代码
class Solution {
public:
int maxEnvelopes(vector<vector>& envelopes) {
std::map<int, vector> mWidthToHeights;
for (const auto& v : envelopes)
{
mWidthToHeights[v[0]].push_back(v[1]);
}
int iMax = 1;
std::map<int, int> mHeightNum;
for ( auto& it : mWidthToHeights)
{
sort(it.second.begin(), it.second.end(),std::greater());
for (auto& height : it.second)
{
auto it = mHeightNum.lower_bound(height);
int iNum =1;
if (mHeightNum.begin() != it)
{//没有套
auto ij = it;
–ij;
iNum = ij->second + 1;
}
iNum = max(iNum,mHeightNum[height]);
auto ij = it;
while ( (ij != mHeightNum.end())&& ( ij->second < iNum))
{
ij++;
}
mHeightNum.erase(it, ij);
mHeightNum[height] = max(mHeightNum[height], iNum);
iMax = max(iMax, mHeightNum[height]);
}
}
return iMax;
}
};
扩展阅读
视频课程
有效学习:明确的目标 及时的反馈 拉伸区(难度合适),可以先学简单的课程,请移步CSDN学院,听白银讲师(也就是鄙人)的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快
速形成战斗了,为老板分忧,请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176
相关下载
想高屋建瓴的学习算法,请下载《闻缺陷则喜算法册》doc版
https://download.csdn.net/download/he_zhidan/88348653
| 充满正能量得对大家说 |
|---|
| 闻缺陷则喜是一个美好的愿望,早发现问题,早修改问题,给老板节约钱。 |
| 墨家名称的来源:有所得以墨记之。 |
| 算法终将统治宇宙,而我们统治算法。《喜缺全书》 |
测试环境
操作系统:win7 开发环境: VS2019 C++17
或者 操作系统:win10 开
发环境: VS2022 C++17

相关文章:

C++二分查找算法的应用:俄罗斯套娃信封问题
本文涉及的基础知识点 二分查找 题目 给你一个二维整数数组 envelopes ,其中 envelopes[i] [wi, hi] ,表示第 i 个信封的宽度和高度。 当另一个信封的宽度和高度都比这个信封大的时候,这个信封就可以放进另一个信封里,如同俄罗…...

redis如何保证和mysql数据的一致性
Redis和MySQL是两种不同的数据库系统,它们在数据一致性方面有不同的特点和应用场景。保证Redis和MySQL数据的一致性通常需要考虑以下几个方面: 双写策略: 一种常见的方法是采用双写策略,即将更新操作同时写入Redis和MySQL。这确保…...

SpringBoot整合Redisson,赶紧整起来!
SpringBoot整合Redisson 一、Redisson 是什么?二、使用场景三、使用步骤1.引入相关依赖2.application.yml配置3.创建RedissonConfig4.开始使用 总结 提示:以下是本篇文章正文内容 一、Redisson 是什么? Redisson是一个基于Java的开源的、高…...

测试Whisper效果
先去官方上面看看,是否有对应的测试结果 简单找了一下,没找到对应的测试数据 去hugging face 上面找对应的数据集,发现没有现成的数据 找到了几个数据集,但是是收费的 101 Hours – Scene Noise Data by Voice Recorder 1,29…...
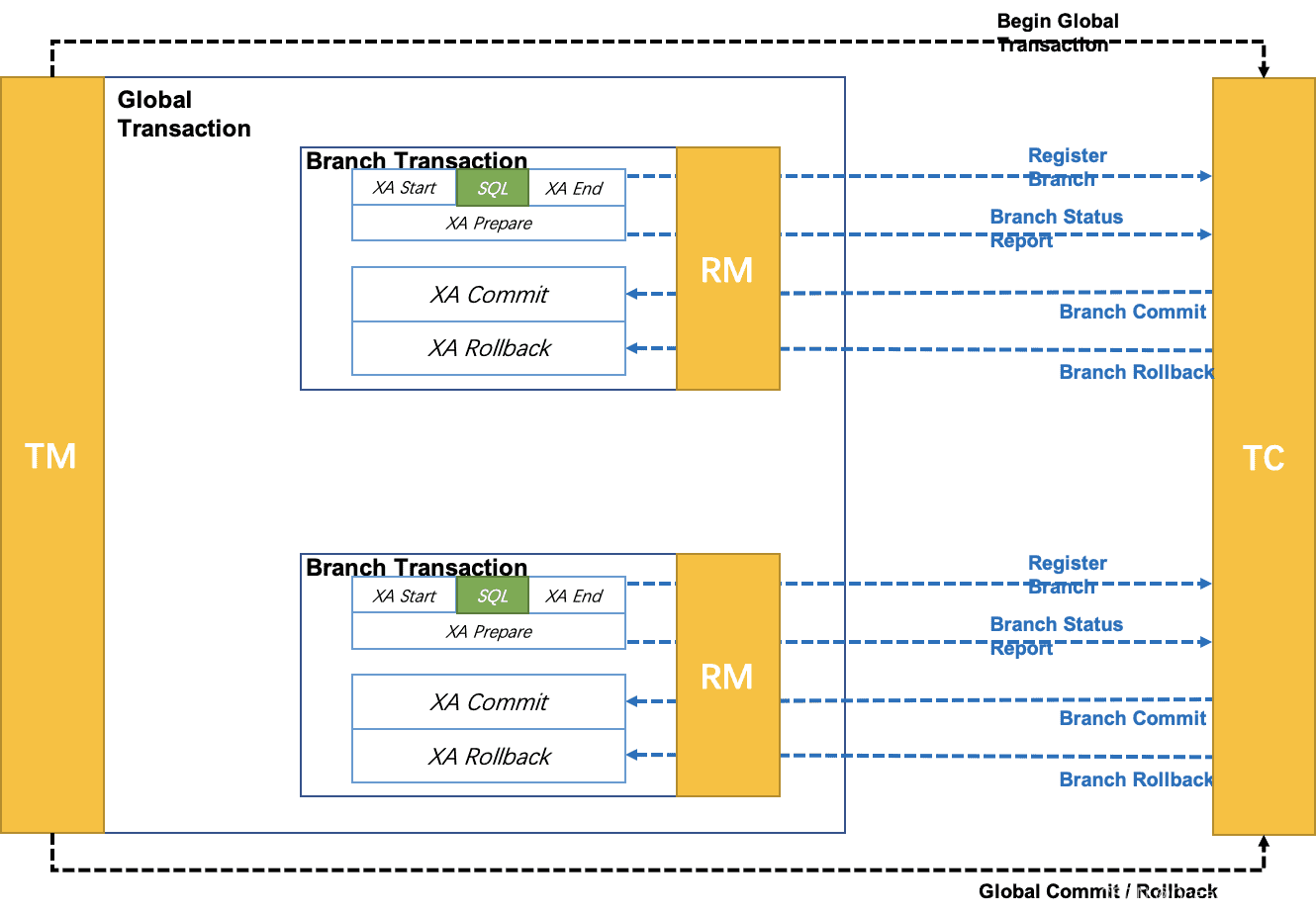
Seata 四种事务模式
Seata 是一款开源的分布式事务解决方案,致力于提供高性能和简单易用的分布式事务服务。Seata 将为用户提供了 AT、TCC、SAGA 和 XA 事务模式,为用户打造一站式的分布式解决方案。 全文参考文献:中文文档 TC (Transaction Coordinator) - 事务…...
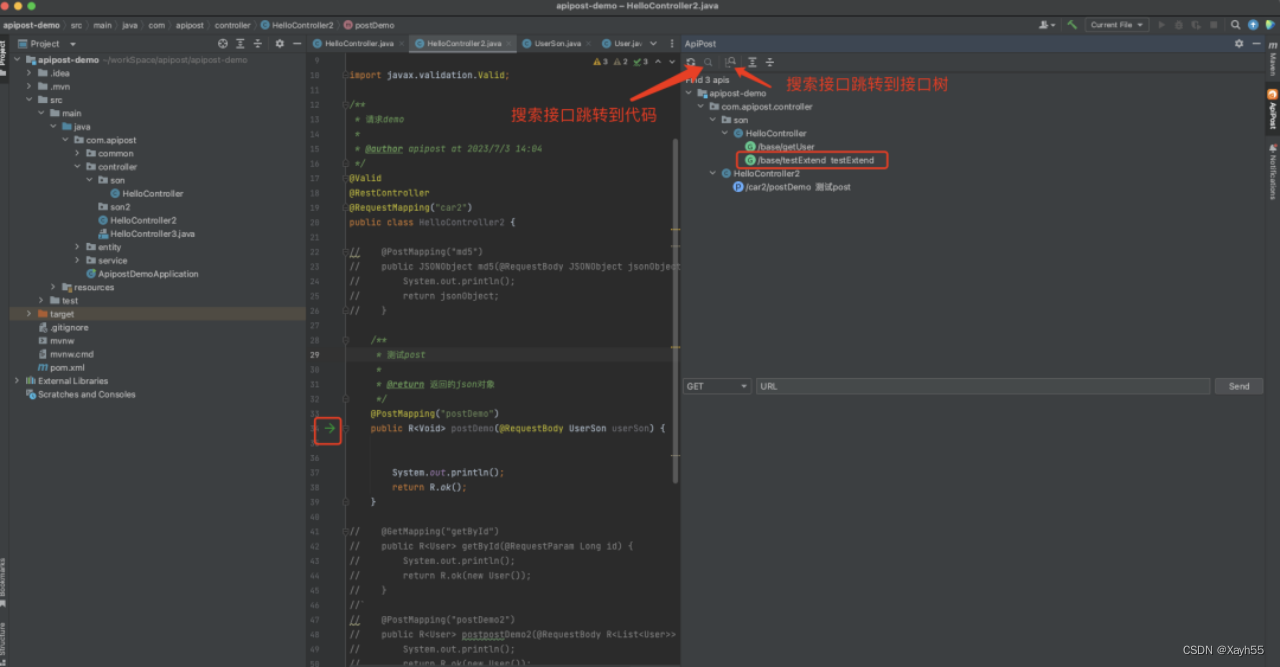
超好用的IDEA插件推荐,写完代码直接调试接口
Apipost推出IDEA插件非常省时高效,写完代码直接可以进行调试,而且支持生成接口文档,真是后端神器啊! 可以点击下方链接安装更新或在插件商店中搜索安装 下载链接:https://plugins.jetbrains.com/plugin/22676-apipos…...

发送post请求、携带cookie、响应对象、高级用法
发送post请求 请求体中,两种方式:data{} ⇢ \dashrightarrow ⇢ 编码格式 urlencoded ⇢ \dashrightarrow ⇢ keyvalue&keyvaluejson{} ⇢ \dashrightarrow ⇢ 编码格式是json 使用方式: resrequests.post(url) 模拟登录 import …...
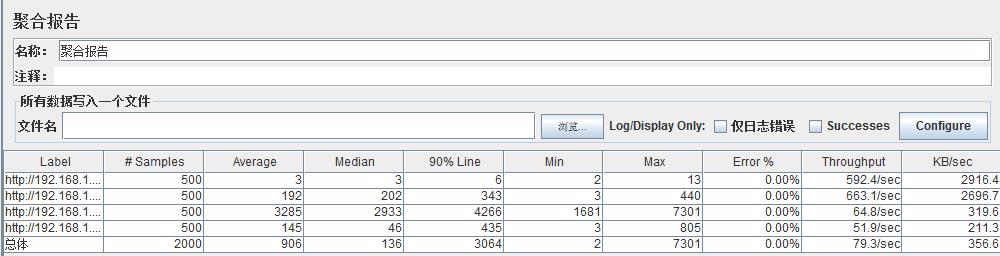
JMeter接口测试性能测试
目前最新版本发展到5.0版本,需要Java7以上版本环境,下载解压目录后,进入\apache-jmeter-5.0\bin\,双击ApacheJMeter.jar文件启动JMemter。 1、创建测试任务 添加线程组,右击测试计划,在快捷菜单单击添加-…...

MongoDB——MongoDB删除系统自带的local数据库
一、MongoDB删除系统自带的local数据库 1.1、linux环境进入mongo客户端 输入 mongo 命令,进入命令行客户端 进入admin库,并登录,查看所有数据库 #进入admin库 use admin #并登录admin db.auth("username","password")…...
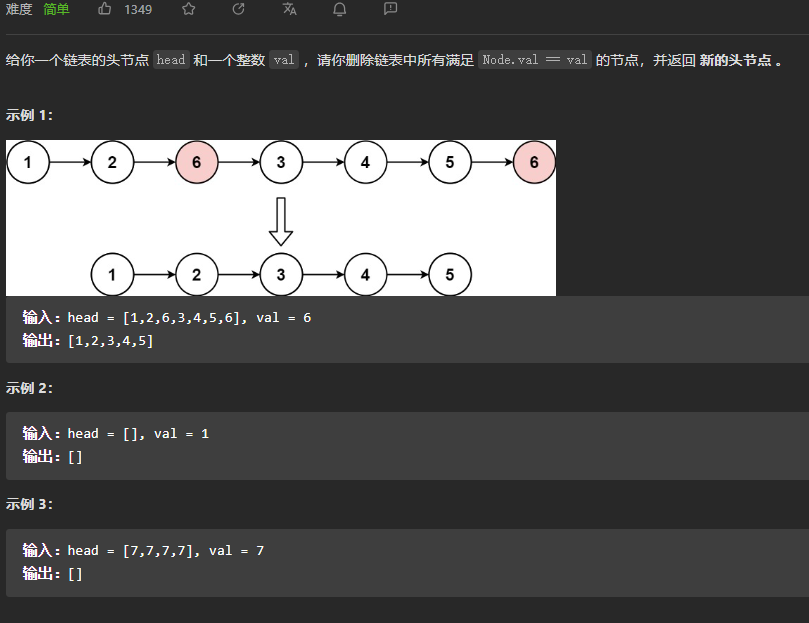
【LeetCode刷题-链表】--203.移除链表元素
203.移除链表元素 方法:定义一个节点指向头节点head,避免头结点单独操作 /*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode() {}* ListNode(int val) { this.val val; }* …...

Microsoft Dynamics 365 CE 扩展定制 - 3. SDK企业功能
在本章中,我们将介绍以下内容: 服务器端并发控制客户端并发控制在事务中执行请求批处理请求暂存数据导入创建早期绑定的实体类扩展CrmSvcUtil用Filter扩展CrmSvcUtil以生成选项集枚举使用CRM配置迁移工具跨实例迁移配置简介 回顾Dynamics CRM的历史,该产品经过多年的发展以…...

人工智能基础_机器学习016_BGD批量梯度下降求解多元一次方程_使用SGD随机梯度下降计算一元一次方程---人工智能工作笔记0056
然后上面我们用BGD计算了一元一次方程,那么现在我们使用BGD来进行计算多元一次方程 对多元一次方程进行批量梯度下降. import numpy as np X = np.random.rand(100,8) 首先因为是8元一次方程,我们要生成100行8列的X的数据对应x1到x8 w = np.random.randint(1,10,size = (8…...

硬件测试(二):波形质量
一、信号质量测试 信号在传输的过程中,一般不是标准的矩形波信号,信号质量测试即通过示波器测试单板硬件的数字信号和模拟信号的各项指标,包括电源、时钟、复位、CPU小系统、外部接口(USB、网口、串口)、逻辑芯片(CPLD…...
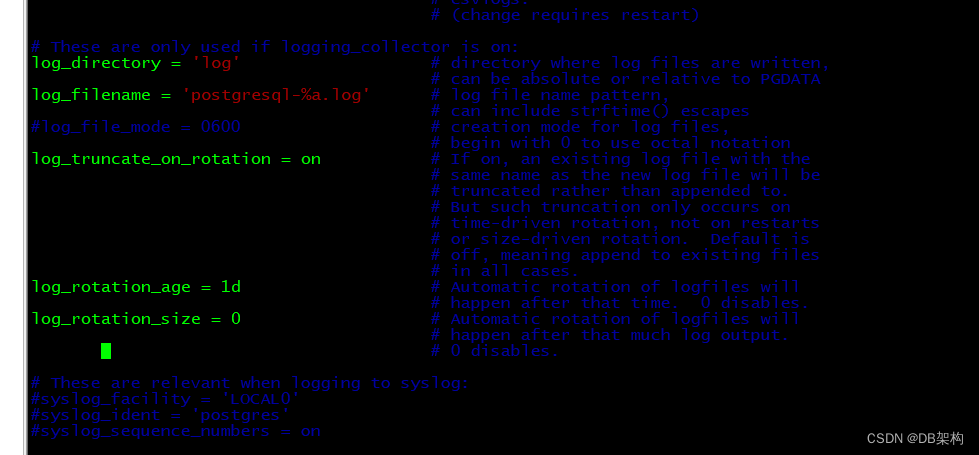
PostgreSQL 数据库日志相关参数
PostgreSQL数据库的配置主要是通过修改数据目录下的 postgresql.conf和pg_hba.conf文件来实现的。 如果想从其他机器上登录该数据 库,需要把监听地址改成实际网络的地址,一种简单的方法是把地址 改成“*”,表示在本地的所有地址上监听&#…...

delete请求,express获取req.body失败
使用 Express 框架处理 DELETE 请求时,通常情况下是不会有请求体的。DELETE 请求通常用于删除资源,而不是发送数据。因此, Express 默认情况下不会解析 DELETE 请求的请求体。 如果需要在 DELETE 请求中发送数据,一种常见的做法是…...

2023年江西省职业院校技能竞赛“网络安全”赛项样题
二、竞赛注意事项 1.竞赛期间禁止携带和使用移动存储设备、计算器、通信工具及 参考资料。 2.请根据大赛所提供的竞赛环境,检查所列的硬件设备、软件清 单、材料清单是否齐全,计算机设备是否能正常使用。 3.在进行任何操作之前,请阅读每个部分…...

groovy下载与安装
Groovy是一种基于JVM(Java虚拟机)的敏捷开发语言,它结合了Python、Ruby和Smalltalk的许多强大的特性,Groovy 代码能够与 Java 代码很好地结合,也能用于扩展现有代码。由于其运行在 JVM 上的特性,Groovy也可…...

Hugging Face LLM部署大语言模型到亚马逊云科技Amazon SageMaker推理示例
本篇文章主要介绍如何使用新的Hugging Face LLM推理容器将开源LLMs,比如BLOOM大型语言模型部署到亚马逊云科技Amazon SageMaker进行推理的示例。我们将部署12B Open Assistant Model,这是一款由开放助手计划训练的开源Chat LLM。 这个示例包括࿱…...

内向基环树
例题1 例题2...
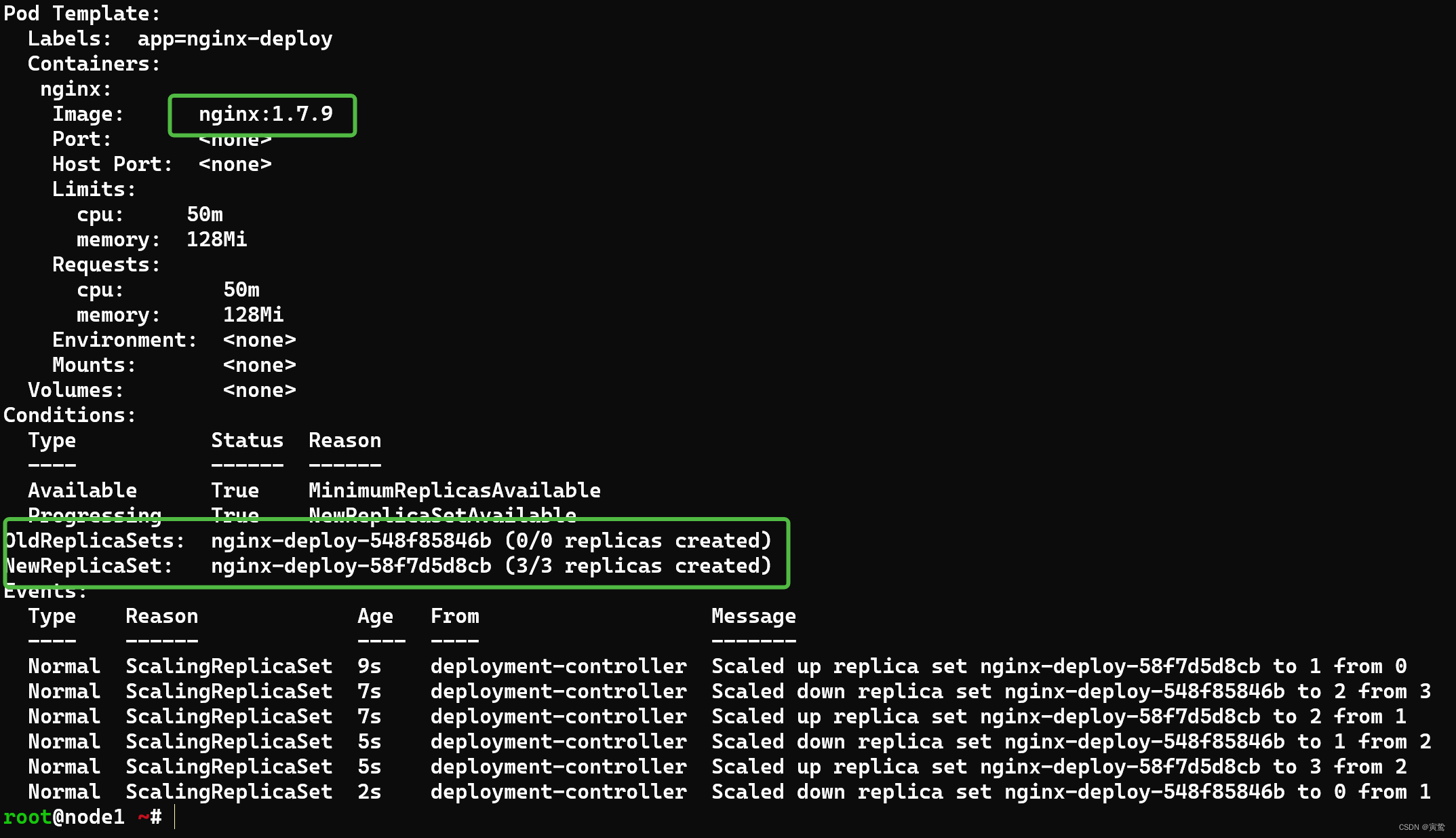
k8s replicaSet,deployment 学习笔记
文章目录 replicaSet 和 deployment 两者的关系。创建滚动更新回滚 replicaSet 和 deployment 两者的关系。 在 Kubernetes 中,ReplicaSet 和 Deployment 都是用来确保某种 Pod 的副本数目。但是,ReplicaSet 和 Deployment 是有差别的,二者的…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...
