Leetcode 673. 最长递增子序列的个数 C++
673最长递增子序列的个数
给定一个未排序的整数数组 nums , 返回最长递增子序列的个数 。
注意 这个数列必须是 严格 递增的。
示例 1:
-
输入: [1,3,5,4,7]
输出: 2
解释: 有两个最长递增子序列,分别是 [1, 3, 4, 7] 和[1, 3, 5, 7]。
示例 2: -
输入: [2,2,2,2,2]
输出: 5
解释: 最长递增子序列的长度是1,并且存在5个子序列的长度为1,因此输出5。
提示:
1 <= nums.length <= 2000
-106 <= nums[i] <= 106
C++代码
#include<iostream>
#include<vector>
using namespace std;
int findNumberOfLIS(vector<int>& nums) {int ans = 0 ;int n = nums.size();vector<int> dp(n+1,1);vector<int> count(n+1,1); //统计当前dp有几个来源 int maxsq = 1;if(n==0){return 0;}if(n==1){return 1;}for(int i=0;i<n;i++){count[0] = 1;for(int j = 0;j<=i;j++){//dp[all] 初始化都是1,如果是递减序列,最长递增子序列所有位子都是1 if(nums[j]<nums[i]){//nums[j]<nums[i],这个是递增子串的前提条件 /*计算最长递增子串的长度*/ if(dp[i] < dp[j]+1) {//1.i>j,但是 j位置到i 位置有一个递增序列,因此i位置的递增子序列长度需要+1dp[i]=dp[j]+1; //3.这种情况,只是产生了子序列长度的增加,路数集成j位子的就可以了count[i] = count[j];//写一个跟屁虫,用于跟踪最长子序列长度最大的是谁if(dp[i]>maxsq){maxsq = dp[i];} }else if(dp[i] == dp[j]+1){//2.说明在j位置之前,有一x个到i长度为dp[j]+1递增序列了//因此说明还有一个相同长度的递增子序列长度count[i]=count[i] + count[j];//nums[j]<nums[i],这个条件会产生递增序列// count[i] 记录了在j之前dp[j]+1长度递增序列的长度// count[j] 表示到达j位子的最长子序列长度的个数// 实现的功能就是到达i位置的每一路递增子序列有多少路 }}}}//遍历conut 表,判断条件是 maxsq =dp[i],最大子序列所在位子 for(int k=0;k<n;k++){if(maxsq ==dp[k]){//说明这里有最长序列的位置 ans = ans + count[k]; }} return ans;}int main(){vector<int> nums;std::vector<int> dnums;int arr[] = {2,2,2,2,2};int arrSize = sizeof(arr) / sizeof(arr[0]);for (int i = 0; i < arrSize; ++i) {dnums.push_back(arr[i]);}int a = findNumberOfLIS(dnums);cout<<a<<endl;return 0;
}
相关文章:

Leetcode 673. 最长递增子序列的个数 C++
673最长递增子序列的个数 给定一个未排序的整数数组 nums , 返回最长递增子序列的个数 。 注意 这个数列必须是 严格 递增的。 示例 1: 输入: [1,3,5,4,7] 输出: 2 解释: 有两个最长递增子序列,分别是 [1, 3, 4, 7] 和[1, 3, 5, 7]。 示例 2: 输入: …...

html用css grid实现自适应四宫格放视频
想同时播放四个本地视频: 四宫格;自式应,即放缩浏览器时,四宫格也跟着放缩;尽量填满页面(F11 浏览器全屏时可以填满整个屏幕)。 在 html 中放视频用 video 标签,参考 [1]࿱…...

【机器学习可解释性】5.SHAP值的高级使用
机器学习可解释性 1.模型洞察的价值2.特征重要性排列3.部分依赖图4.SHAP 值5.SHAP值的高级使用 正文 汇总SHAP值以获得更详细的模型解释 总体回顾 我们从学习排列重要性和部分依赖图开始,以显示学习后的模型的内容。 然后我们学习了SHAP值来分解单个预测的组成部…...

CentOS开机自动运行jar程序实现
前面已经有一篇文章介绍jar包如何在CentOS上运行,《在linux上运行jar程序操作记录》 后来发现系统重启后不能自动运行,导致每次都要手动打开,这篇介绍如何自动开机启动运行jar程序。 一、找到JDK程序执行位置 [rootlocalhost /]# which jav…...
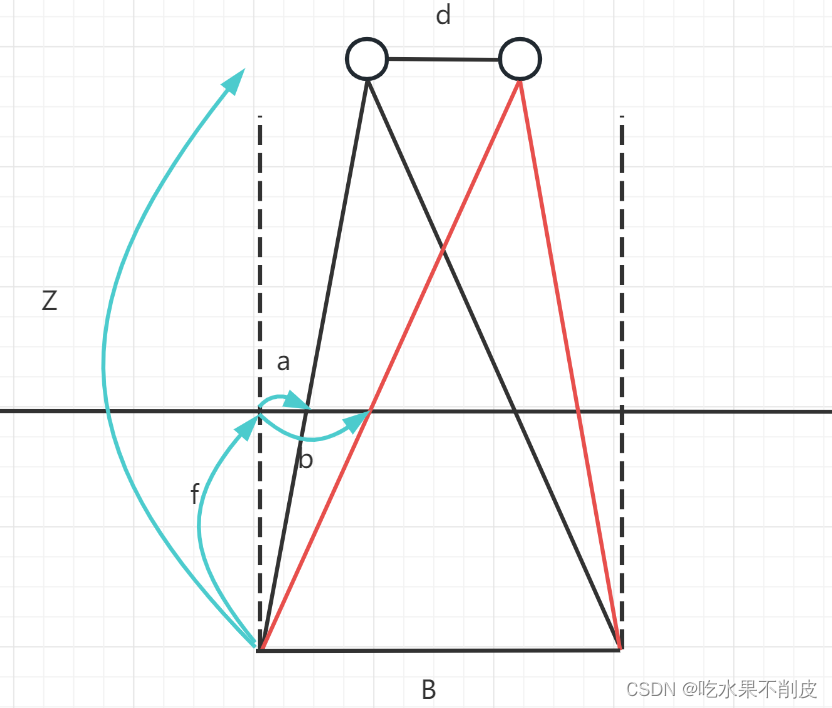
matlab双目标定中基线物理长度获取
在MATLAB进行双目摄像机标定时,通常会获得相机的内参,其中包括像素单位的焦距(focal length)以及物理单位的基线长度(baseline)。对于应用中的深度估计和测量,基线长度的物理单位非常重要,因为它直接影响到深度信息的准确性。有时候,您可能只能获取像素单位的焦距和棋…...

自己动手实现一个深度学习算法——二、神经网络的实现
文章目录 1. 神经网络概述1)表示2)激活函数3)sigmoid函数4)阶跃函数的实现5)sigmoid函数的实现6)sigmoid函数和阶跃函数的比较7)非线性函数8)ReLU函数 2.三层神经网络的实现1)结构2&…...
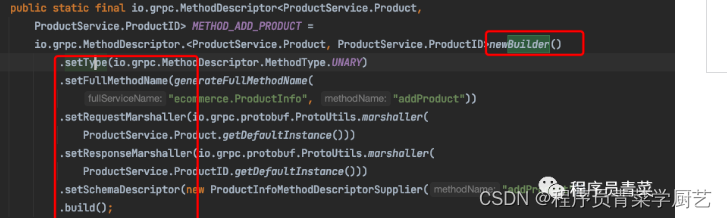
gRPC源码剖析-Builder模式
一、Builder模式 1、定义 将一个复杂对象的构建与表示分离,使得同样的构建过程可以创建不同的的表示。 2、适用场景 当创建复杂对象的算法应独立于该对象的组成部分以及它们的装配方式时。 当构造过程必须允许被构造的对象有不同的表示时。 说人话:…...

ARM传输数据以及移位操作
3.2.2 数据传送指令 LDR/STR指令用来在寄存器和内存之间输送数据。如果我们想要在寄存器之间传送数据,则可以使用MOV指令。MOV指令的格式如下。 MOV {cond} {s}Rd, oprand2 MOV {cond} {s}Rd, oprand2 其中,{cond}为条件指令可选项,{s}用来表…...
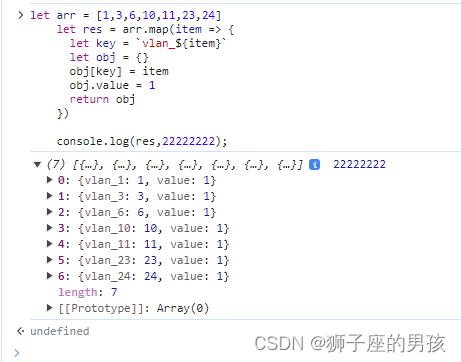
06、如何将对象数组里 obj 的 key 值变成动态的(即:每一个对象对应的 key 值都不同)
1、数据情况: 其一、从后端拿到的数据为: let arr [1,3,6,10,11,23,24] 其二、目标数据为: [{vlan_1: 1, value: 1}, {vlan_3: 3, value: 1}, {vlan_6: 6, value: 1}, {vlan_10: 10, value: 1}, {vlan_11: 11, value: 1}, {vlan_23: 23, v…...
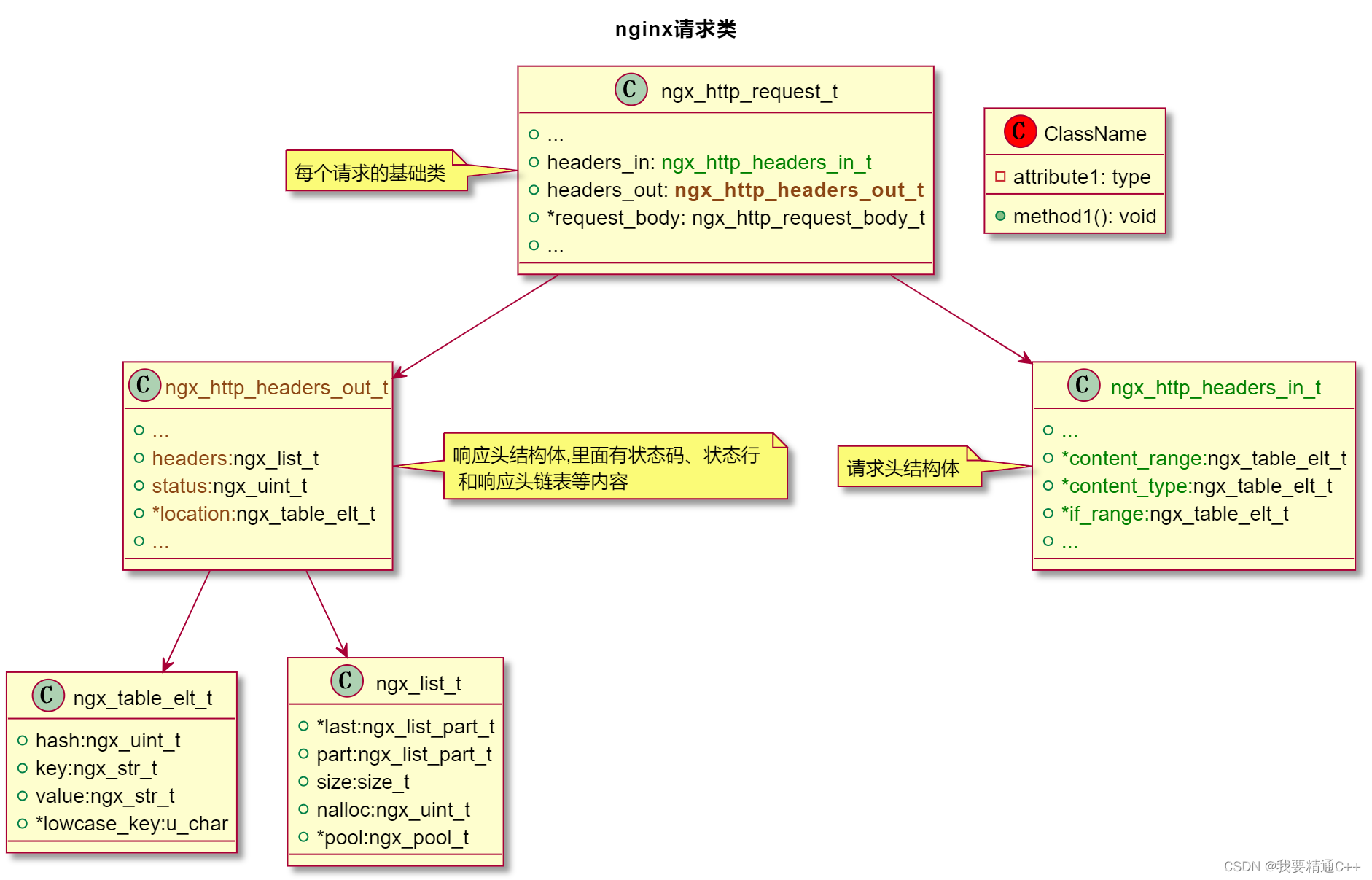
ngx_http_request_s
/* 罗剑锋老师的注释参考: https://github.com/chronolaw/annotated_nginx/blob/master/nginx/src/http/ngx_http_request.h */struct ngx_http_request_s {uint32_t signature; /* "HTTP" */ngx_connection_t …...

Docker 学习路线 2:底层技术
了解驱动Docker的核心技术将让您更深入地了解Docker的工作原理,并有助于您更有效地使用该平台。 Linux容器(LXC) Linux容器(LXC)是Docker的基础。 LXC是一种轻量级的虚拟化解决方案,允许多个隔离的Linux系…...

UEFI实战——显示图片
一、准备工作 1.1 BMP格式图片 参考:BMP格式详解获取“BMP格式详解”文档里的图片,命名为Logo.bmp将Logo.bmp图片放到U盘里,U盘格式FAT32二、实例代码 2.1 代码结构 TextPkg/ ├── Display.c ├── GetFile.c ├── Test.c ├── Test.dsc ├── Test.h └── Tes…...
Ansible中的playbook
目录 一、playbook简介 二、playbook的语法 三、playbook的核心组件 四、playbook的执行命令 五、vim 设定技巧 六、基本示例 一、playbook简介 1、playbook与ad-hoc相比,是一种完全不同的运用。 2、playbook是一种简单的配置管理系统与多机器部署系统的基础…...
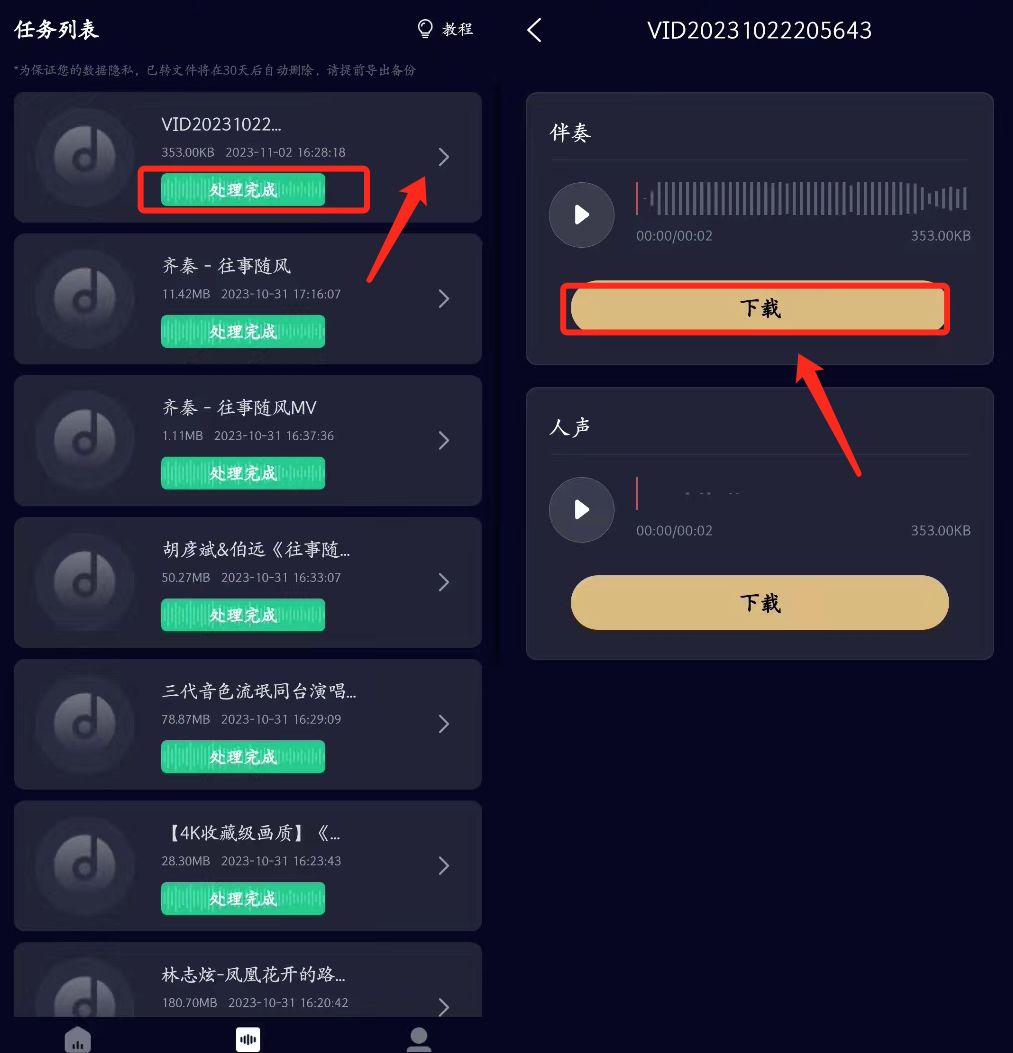
怎样去除视频中的杂音,保留人声部分?
怎样去除视频中的杂音,保留人声部分?这个简单嘛!两种办法可以搞定:一是进行音频降噪,把无用的杂音消除掉;二是提取人声,将要保留的人声片段提取出来。 这就将两种实用的办公都分享出来…...
基于Qt QTreeView|QTreeWidget控件使用简单版
头文件解析: 这是一个C++代码文件,定义了一个名为MainWindow的类。以下是对每一句的详细解释: ```cpp #ifndef MAINWINDOW_H #define MAINWINDOW_H ``` 这是一个条件编译指令,用于避免头文件的重复包含。`MAINWINDOW_H`是一个宏定义,用于唯一标识这个头文件。 ```cpp #…...
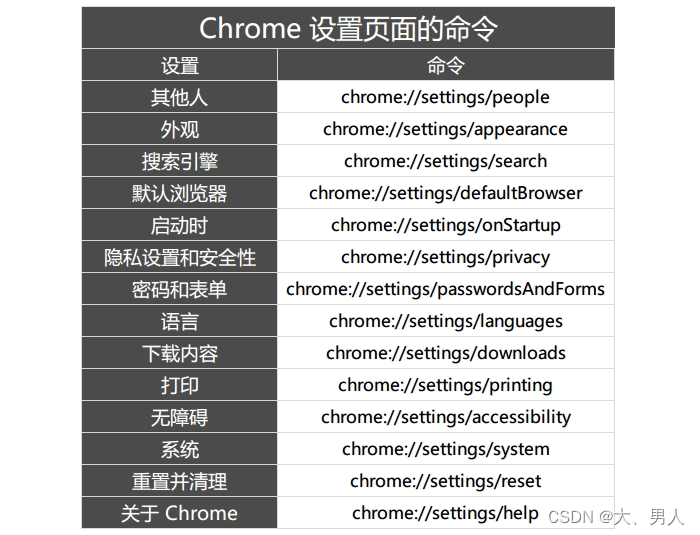
edge浏览器的隐藏功能
1. edge://version 查看版本信息 2. edge://flags 特性界面 具体到某一特性:edge://flags/#overlay-scrollbars 3. edge://settings设置界面 详情可参考chrome: 4. edge://extensions 扩展程序页面 5. edge://net-internals 网络事件信息 6. edge://component…...
安卓抓包之小黄鸟
下载安装 下载地址: https://download.csdn.net/download/yijianxiangde100/88496463 安装apk 即可。 证书配置:...

Django中的FBV和CBV
一、两者的区别 1、在我们日常学习Django中,都是用的FBV(function base views)方式,就是在视图中用函数处理各种请求。而CBV(class base view)则是通过类来处理请求。 2、Python是一个面向对象的编程语言…...

信息泄露--
大唐电信AC简介 大唐电信科技股份有限公司是电信科学技术研究院(大唐电信科技产业集团)控股的的高科技企业,大唐电信已形成集成电路设计、软件与应用、终端设计、移动互联网四大产业板块。 大唐电信AC集中管理平台存在弱口令及敏感信息泄漏漏…...

C#WPF文本格式化模式实例
本文演示C#WPF文本格式化模式实例 WPF 文本渲染优缺点 WPF中的文本渲染和旧式的基于 GDI的应用程序的文本染有很大区别。很大一部分区 别是由于 WPF 的设备无关显示系统造成的,但 WPF 中的文本染也得到了显著增强,能更清晰地显示文本,在 LCD 监视器上尤其如此。 然而,W…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...

使用SSE解决获取状态不一致问题
使用SSE解决获取状态不一致问题 1. 问题描述2. SSE介绍2.1 SSE 的工作原理2.2 SSE 的事件格式规范2.3 SSE与其他技术对比2.4 SSE 的优缺点 3. 实战代码 1. 问题描述 目前做的一个功能是上传多个文件,这个上传文件是整体功能的一部分,文件在上传的过程中…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...
