时间复杂度为 O(nlogn) 的排序算法
归并排序
归并排序遵循 分治 的思想:将原问题分解为几个规模较小但类似于原问题的子问题,递归地求解这些子问题,然后合并这些子问题的解来建立原问题的解,归并排序的步骤如下:
-
划分:分解待排序的 n 个元素的序列成各具 n/2 个元素的两个子序列,将长数组的排序问题转换为短数组的排序问题,当待排序的序列长度为 1 时,递归划分结束
-
合并:合并两个已排序的子序列得出已排序的最终结果
归并排序的代码实现如下:
private void sort(int[] nums, int left, int right) {if (left >= right) {return;}// 划分int mid = left + right >> 1;sort(nums, left, mid);sort(nums, mid + 1, right);// 合并merge(nums, left, mid, right);}private void merge(int[] nums, int left, int mid, int right) {// 辅助数组int[] temp = Arrays.copyOfRange(nums, left, right + 1);int leftBegin = 0, leftEnd = mid - left;int rightBegin = leftEnd + 1, rightEnd = right - left;for (int i = left; i <= right; i++) {if (leftBegin > leftEnd) {nums[i] = temp[rightBegin++];} else if (rightBegin > rightEnd || temp[leftBegin] < temp[rightBegin]) {nums[i] = temp[leftBegin++];} else {nums[i] = temp[rightBegin++];}}}
归并排序最吸引人的性质是它能保证将长度为 n 的数组排序所需的时间和 nlogn 成正比;它的主要缺点是所需的额外空间和 n 成正比。
算法特性:
-
空间复杂度:借助辅助数组实现合并,使用 O(n) 的额外空间;递归深度为 logn,使用 O(logn) 大小的栈帧空间。忽略低阶部分,所以空间复杂度为 O(n)
-
非原地排序
-
稳定排序
-
非自适应排序
以上代码是归并排序常见的实现,下面我们来一起看看归并排序的优化策略:
将多次创建小数组的开销转换为只创建一次大数组
在上文实现中,我们在每次合并两个有序数组时,即使是很小的数组,我们都会创建一个新的 temp[] 数组,这部分耗时是归并排序运行时间的主要部分。更好的解决方案是将 temp[] 数组定义成 sort() 方法的局部变量,并将它作为参数传递给 merge() 方法,实现如下:
private void sort(int[] nums, int left, int right, int[] temp) {if (left >= right) {return;}// 划分int mid = left + right >> 1;sort(nums, left, mid, temp);sort(nums, mid + 1, right, temp);// 合并merge(nums, left, mid, right, temp);}private void merge(int[] nums, int left, int mid, int right, int[] temp) {System.arraycopy(nums, left, temp, left, right - left + 1);int l = left, r = mid + 1;for (int i = left; i <= right; i++) {if (l > mid) {nums[i] = temp[r++];} else if (r > right || temp[l] < temp[r]) {nums[i] = temp[l++];} else {nums[i] = temp[r++];}}}
当数组有序时,跳过 merge() 方法
我们可以在执行合并前添加判断条件:如果 nums[mid] <= nums[mid + 1] 时我们认为数组已经是有序的了,那么我们就跳过 merge() 方法。它不影响排序的递归调用,但是对任意有序的子数组算法的运行时间就变成线性的了,代码实现如下:
private void sort(int[] nums, int left, int right, int[] temp) {if (left >= right) {return;}// 划分int mid = left + right >> 1;sort(nums, left, mid, temp);sort(nums, mid + 1, right, temp);// 合并if (nums[mid] > nums[mid + 1]) {merge(nums, left, mid, right, temp);}}private void merge(int[] nums, int left, int mid, int right, int[] temp) {System.arraycopy(nums, left, temp, left, right - left + 1);int l = left, r = mid + 1;for (int i = left; i <= right; i++) {if (l > mid) {nums[i] = temp[r++];} else if (r > right || temp[l] < temp[r]) {nums[i] = temp[l++];} else {nums[i] = temp[r++];}}}
对小规模子数组使用插入排序
对小规模数组进行排序会使递归调用过于频繁,而使用插入排序处理小规模子数组一般可以将归并排序的运行时间缩短 10% ~ 15%,代码实现如下:
/*** M 取值在 5 ~ 15 之间大多数情况下都能令人满意*/private final int M = 9;private void sort(int[] nums, int left, int right) {if (left + M >= right) {// 插入排序insertSort(nums);return;}// 划分int mid = left + right >> 1;sort(nums, left, mid);sort(nums, mid + 1, right);// 合并merge(nums, left, mid, right);}/*** 插入排序*/private void insertSort(int[] nums) {for (int i = 1; i < nums.length; i++) {int base = nums[i];int j = i - 1;while (j >= 0 && nums[j] > base) {nums[j + 1] = nums[j--];}nums[j + 1] = base;}}private void merge(int[] nums, int left, int mid, int right) {// 辅助数组int[] temp = Arrays.copyOfRange(nums, left, right + 1);int leftBegin = 0, leftEnd = mid - left;int rightBegin = leftEnd + 1, rightEnd = right - left;for (int i = left; i <= right; i++) {if (leftBegin > leftEnd) {nums[i] = temp[rightBegin++];} else if (rightBegin > rightEnd || temp[leftBegin] < temp[rightBegin]) {nums[i] = temp[leftBegin++];} else {nums[i] = temp[rightBegin++];}}}
快速排序
快速排序也遵循 分治 的思想,它与归并排序不同的是,快速排序是 原地排序,而且快速排序会先排序当前数组,再对子数组进行排序,它的算法步骤如下:
-
哨兵划分:选取数组中最左端元素为基准数,将小于基准数的元素放在基准数左边,将大于基准数的元素放在基准数右边
-
排序子数组:将哨兵划分的索引作为划分左右子数组的分界,分别对左右子数组进行哨兵划分和排序
快速排序的代码实现如下:
private void sort(int[] nums, int left, int right) {if (left >= right) {return;}// 哨兵划分int partition = partition(nums, left, right);// 分别排序两个子数组sort(nums, left, partition - 1);sort(nums, partition + 1, right);}/*** 哨兵划分*/private int partition(int[] nums, int left, int right) {// 以 nums[left] 作为基准数,并记录基准数索引int originIndex = left;int base = nums[left];while (left < right) {// 从右向左找小于基准数的元素while (left < right && nums[right] >= base) {right--;}// 从左向右找大于基准数的元素while (left < right && nums[left] <= base) {left++;}swap(nums, left, right);}// 将基准数交换到两子数组的分界线swap(nums, originIndex, left);return left;}private void swap(int[] nums, int left, int right) {int temp = nums[left];nums[left] = nums[right];nums[right] = temp;}
算法特性:
-
时间复杂度:平均时间复杂度为 O(nlogn),最差时间复杂度为 O(n2)
-
空间复杂度:最差情况下,递归深度为 n,所以空间复杂度为 O(n)
-
原地排序
-
非稳定排序
-
自适应排序
归并排序的时间复杂度一直是 O(nlogn),而快速排序在最坏的情况下时间复杂度为 O(n2),为什么归并排序没有快速排序应用广泛呢?
答:因为归并排序是非原地排序,在合并阶段需要借助非常量级的额外空间
快速排序有很多优点,但是在哨兵划分不平衡的情况下,算法的效率会比较低效。下面是对快速排序排序优化的一些方法:
切换到插入排序
对于小数组,快速排序比插入排序慢,快速排序的 sort() 方法在长度为 1 的子数组中也会调用一次,所以,在排序小数组时切换到插入排序排序的效率会更高,如下:
/*** M 取值在 5 ~ 15 之间大多数情况下都能令人满意*/private final int M = 9;public void sort(int[] nums, int left, int right) {// 小数组采用插入排序if (left + M >= right) {insertSort(nums);return;}int partition = partition(nums, left, right);sort(nums, left, partition - 1);sort(nums, partition + 1, right);}/*** 插入排序*/private void insertSort(int[] nums) {for (int i = 1; i < nums.length; i++) {int base = nums[i];int j = i - 1;while (j >= 0 && nums[j] > base) {nums[j + 1] = nums[j--];}nums[j + 1] = base;}}private int partition(int[] nums, int left, int right) {int originIndex = left;int base = nums[left];while (left < right) {while (left < right && nums[right] >= base) {right--;}while (left < right && nums[left] <= base) {left++;}swap(nums, left, right);}swap(nums, left, originIndex);return left;}private void swap(int[] nums, int left, int right) {int temp = nums[left];nums[left] = nums[right];nums[right] = temp;}
基准数优化
如果数组为倒序的情况下,选择最左端元素为基准数,那么每次哨兵划分会导致右数组长度为 0,进而使快速排序的时间复杂度为 O(n2),为了尽可能避免这种情况,我们可以对基准数的选择进行优化,采用 三取样切分 的方法:选取数组最左端、中间和最右端这三个值的中位数为基准数,这样选择的基准数大概率不是区间的极值,时间复杂度为 O(n2) 的概率大大降低,代码实现如下:
public void sort(int[] nums, int left, int right) {if (left >= right) {return;}// 基准数优化betterBase(nums, left, right);int partition = partition(nums, left, right);sort(nums, left, partition - 1);sort(nums, partition + 1, right);}/*** 基准数优化,将 left, mid, right 这几个值中的中位数换到 left 的位置* 注意其中使用了异或运算进行条件判断*/private void betterBase(int[] nums, int left, int right) {int mid = left + right >> 1;if ((nums[mid] < nums[right]) ^ (nums[mid] < nums[left])) {swap(nums, left, mid);} else if ((nums[right] < nums[left]) ^ (nums[right] < nums[mid])) {swap(nums, left, right);}}private int partition(int[] nums, int left, int right) {int originIndex = left;int base = nums[left];while (left < right) {while (left < right && nums[right] >= base) {right--;}while (left < right && nums[left] <= base) {left++;}swap(nums, left, right);}swap(nums, originIndex, left);return left;}private void swap(int[] nums, int left, int right) {int temp = nums[left];nums[left] = nums[right];nums[right] = temp;}
三向切分
在数组有大量重复元素的情况下,快速排序的递归性会使元素全部重复的子数组经常出现,而对这些数组进行快速排序是没有必要的,我们可以对它进行优化。
一个简单的想法是将数组切分为三部分,分别对应小于、等于和大于基准数的数组,每次将其中“小于”和“大于”的数组进行排序,那么最终也能得到排序的结果,这种策略下我们不会对等于基准数的子数组进行排序,提高了排序算法的效率,它的算法流程如下:
从左到右遍历数组,维护指针 l 使得 [left, l - 1] 中的元素都小于基准数,维护指针 r 使得 [r + 1, right] 中的元素都大于基准数,维护指针 mid 使得 [l, mid - 1] 中的元素都等于基准数,其中 [mid, r] 区间中的元素还未确定大小关系,图示如下:
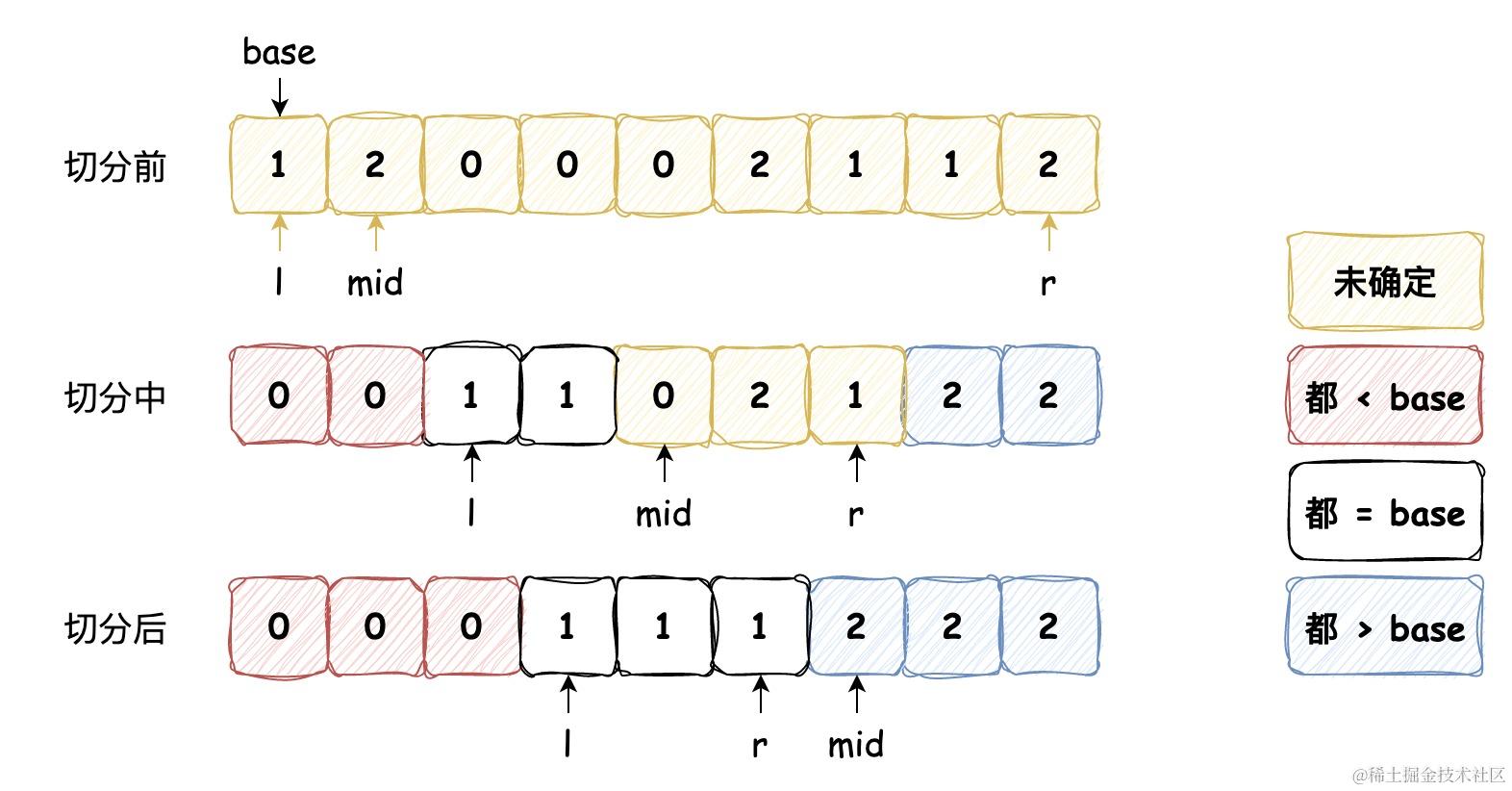
它的代码实现如下:
public void sort(int[] nums, int left, int right) {if (left >= right) {return;}// 三向切分int l = left, mid = left + 1, r = right;int base = nums[l];while (mid <= r) {if (nums[mid] < base) {swap(nums, l++, mid++);} else if (nums[mid] > base) {swap(nums, mid, r--);} else {mid++;}}sort(nums, left, l - 1);sort(nums, r + 1, right);}private void swap(int[] nums, int left, int right) {int temp = nums[left];nums[left] = nums[right];nums[right] = temp;}
这也是经典的荷兰国旗问题,因为这就好像用三种可能的主键值将数组排序一样,这三种主键值对应着荷兰国旗上的三种颜色
巨人的肩膀
-
《Hello 算法》:11.5 和 11.6 小节
-
《算法 第四版》:2.3 节 快速排序
-
《算法导论 第三版》:第 2.2、2.3、7 章
相关文章:

时间复杂度为 O(nlogn) 的排序算法
归并排序 归并排序遵循 分治 的思想:将原问题分解为几个规模较小但类似于原问题的子问题,递归地求解这些子问题,然后合并这些子问题的解来建立原问题的解,归并排序的步骤如下: 划分:分解待排序的 n 个元素…...
掌控你的Mac性能:System Dashboard Pro,一款专业的系统监视器
作为Mac用户,你是否曾经想要更好地了解你的电脑性能,以便优化其运行?是否想要实时监控系统状态,以便及时发现并解决问题?如果你有这样的需求,那么System Dashboard Pro就是你的不二之选。 System Dashboar…...

C++ Qt如何往Windows AppData目录写数据
在使用Qt开发客户端软件时,我们可以把程序相关信息保存到AppData目录, 下次启动时读取,就可以保存程序的状态,便于用户使用。 Windows AppData目录是Windows操作系统中的一个重要目录,主要用于存储应用程序的自定义设置、文件和数据。这个目录包含了许多与应用程序相关的配…...

xargs命令
xargs命令 xargs 命令是一个非常好用的 Linux 命令,它可以将管道或标准输入转换成命令行参数,并用这些参数来执行指定 的命令。默认情况下, xargs 命令会将输入按照空格、制表符、换行符等符号进行分隔,并将它们作为一组参数 传…...
【原创】java+swing+mysql无偿献血管理系统设计与实现
摘要: 无偿献血管理系统是为了实现无偿献血规范化、有序化、高效化的管理而设计的。本文主要介绍使用java语言开发一个基于C/S架构的无偿献血管理系统,提高无偿献血管理的工作效率。 功能分析: 系统主要提供给管理员、无偿献血人员&#x…...

C语言 Number 1 基本数据类型
数据类型的定义 c语言的数据分类基本类型整型浮点型float和double的精度和范围范围精度 枚举类型空类型派生类型派生的一般表达形式 注 c语言的数据分类 首先是针对C语言的数据类型做个整理 大致分为四个大类型 基本类型枚举类型空类型派生类型 那么根据以上四个大类型 我们…...

mac录屏快捷键指南,轻松录制屏幕内容!
“大家知道mac电脑有录屏快捷键吗,现在录屏不太方便,每次都花很多时间,要是有录屏快捷键,应该会快速很多,可是哪里都找不到,有人知道吗?帮帮我!” 苹果的mac电脑以其精美的设计和卓…...
精准测试是个错误
如果你已经了解了精准测试在行业的主流做法,你可以跳过相关内容。 行业里对于精准测试的定义 在网上流传着一些精准测试的定义(如果你对这些定义不感冒,可直接跳到我个人的定义): 自网易陈逸青(2020&#x…...

算法通关村第四关|黄金挑战|表达式问题
1.计算器问题 给定一个内容为表达式的字符串,计算结果。 class Solution {public int calculate(String s) {Deque<Integer> stack new ArrayDeque<Integer>();char preSign ;int num 0;int n s.length();for (int i 0; i < n; i) {if (Chara…...
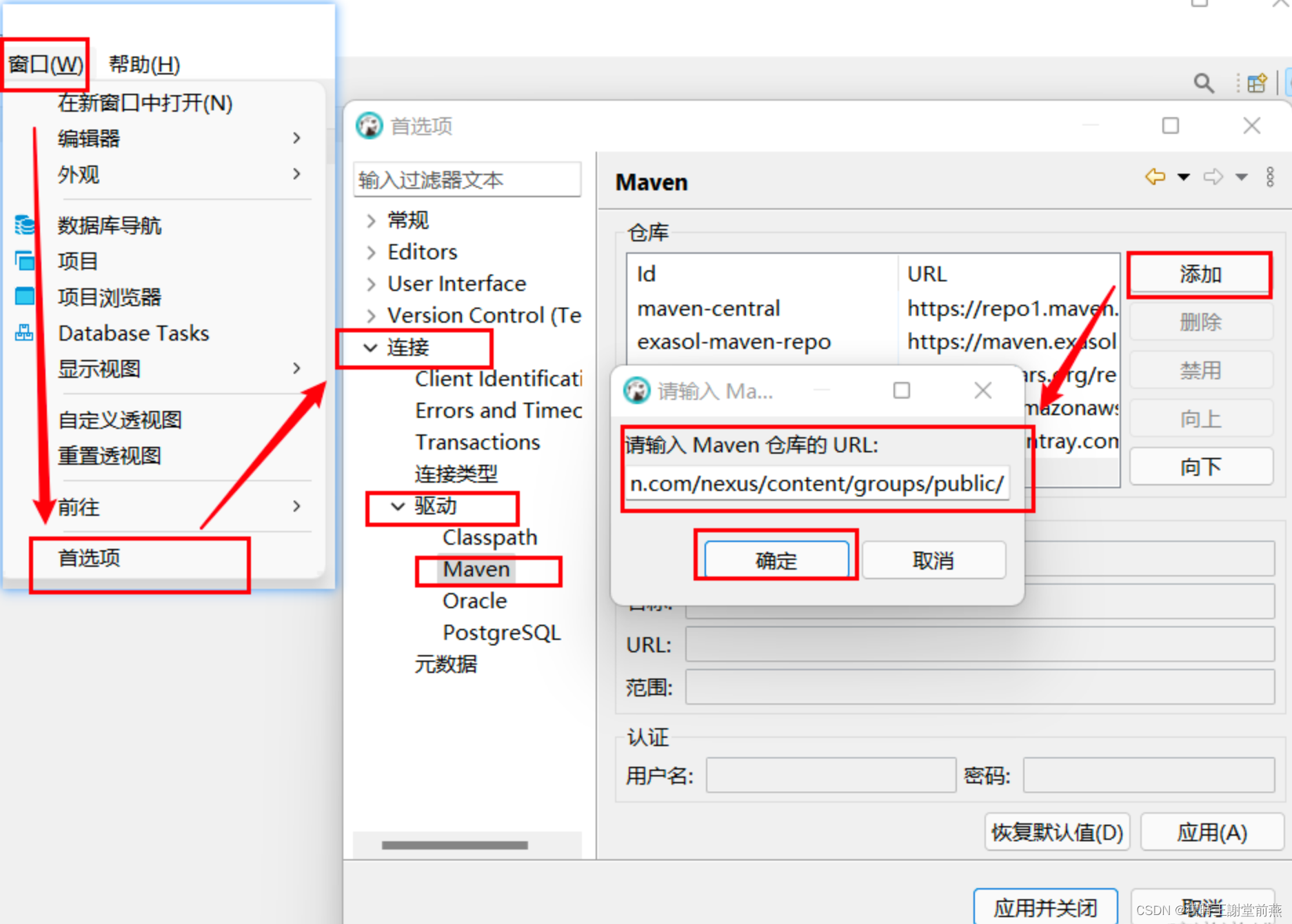
Mac安装DBeaver
目录 一、DBeaver Mac版软件简介 二、下载地址 三、DBeaver连接失败报错 3.1 问题描述 3.2 连接失败问题解决 一、DBeaver Mac版软件简介 DBeaver Mac版是一款专门为开发人员和数据库管理员设计的免费开源通用数据库工具。软件的易用性是它的宗旨,是经过精心设计…...

C++ 类 根据成员变量的指针获取类对象的指针
一.宏定义 实现方式有多种,原理是相同的 方式1: #define get_class_ptr(memberPtr,classType,memberName) \ ((classType*)((char*)(memberPtr)-(unsigned long)((ULONG_PTR)&((classType*)0)->member))) 方式2: #define get_cl…...
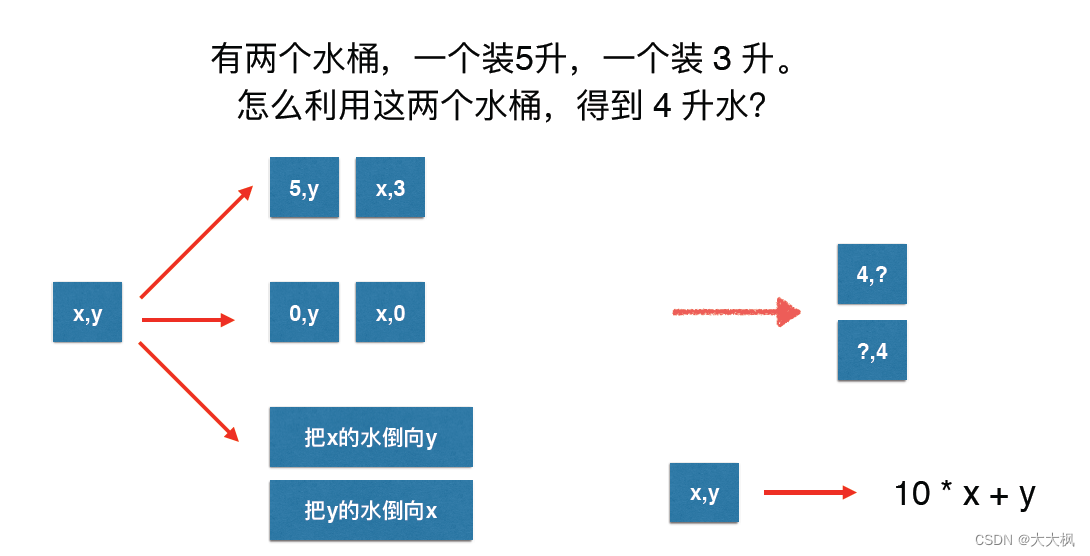
图论08-图的建模-状态的表达与理解 - 倒水问题为例
文章目录 状态的表达例题1题解1 终止条件:有一个数位为42 状态的改变:a表示十位数,b表示个位数3 其他设置 例题2 力扣773 滑动谜题JavaC 状态的表达 例题1 从初始的(x,y)状态,到最后变成(4,&am…...

sqlserver字符串拼接
本文主要介绍了sqlserver字符串拼接的实现,文中通过示例代码介绍的非常详细,对大家的学习或者工作具有一定的参考学习价值。 1. 概 在SQL语句中经常需要进行字符串拼接,以sqlserver,oracle,mysql三种数据库为例&#…...

MySQL-----事务
事务的概念 事务是一种机制,一个操作序列。包含了一组数据库的操作命令,所有的命令都是一个整体,向系统提交或者撤销的操作,要么都执行,要么都不执行。 是一个不可分割的单位 事务的ACID特点 ACID,是指在可…...

hive的安装配置笔记
1.上传hive安装包 2.解压 3.配置Hive(在一台机器上即可) mv hive-env.sh.template hive-env.sh 4.运行hive 发现内置默认的metastore存在问题(1.换执行路径后,原来的表不存在了。2.只能有一个用户访问同一个表) 5.配置mysql的meta…...

lamba stream处理集合
lamba stream处理集合 带拼接多字段分组List< Object> 转 Map<String,List< Object>> Map<String, List<ProfitAndLossMapping>> collect plMappingList.stream() .collect(Collectors.groupingBy(m -> m.getLosType() ":" m.…...
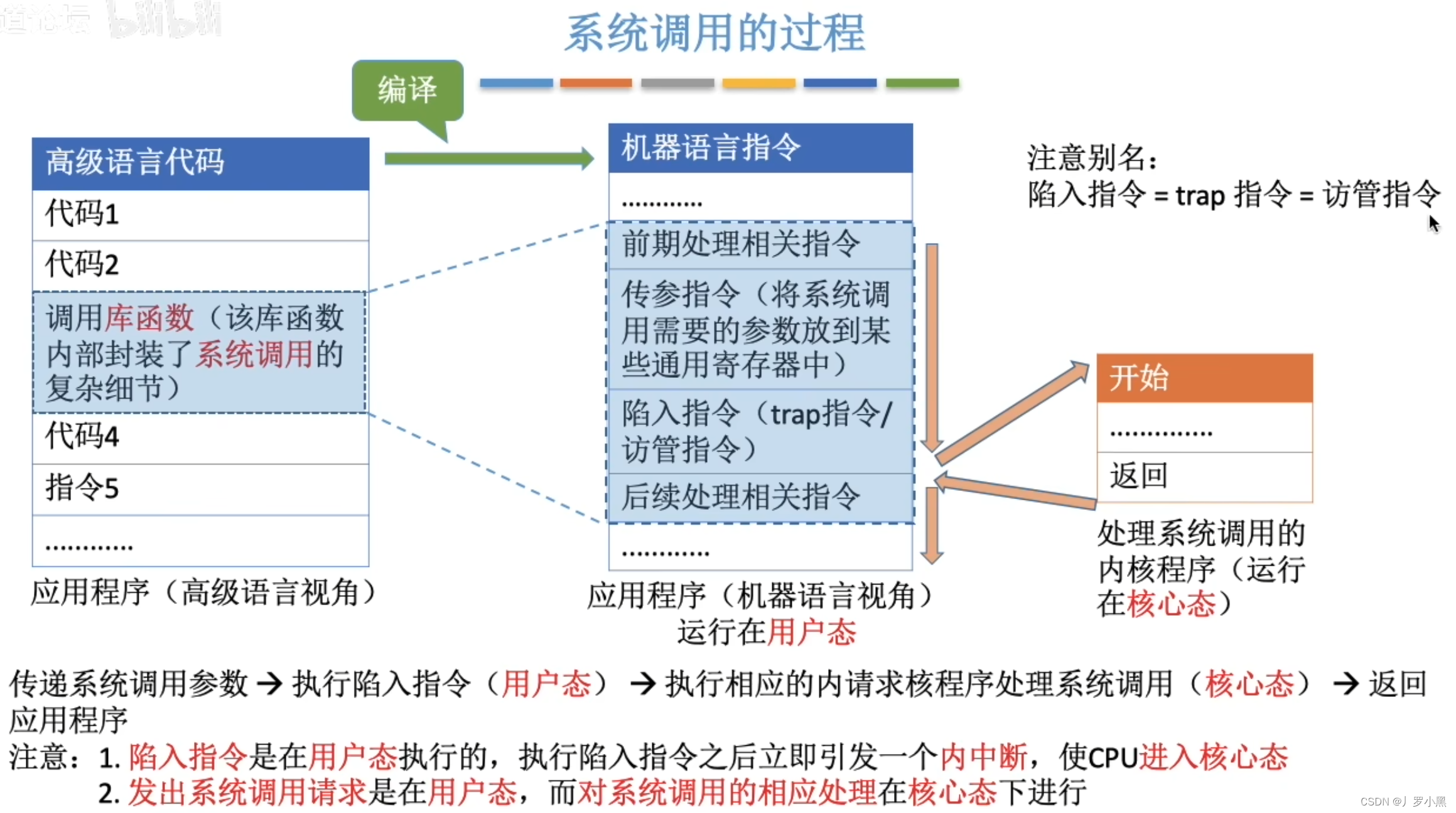
操作系统 day04(系统调用)
什么是系统调用 库函数和系统调用的区别 应用程序可以通过汇编语言直接进行系统调用,也可以使用高级语言的库函数来进行系统调用。而有的库函数涉及系统调用,如“创建一个新文件”函数,有的不涉及,如“取绝对值”函数 什么功能要…...
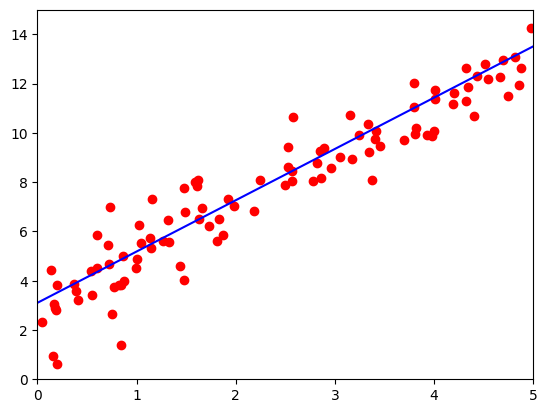
【深度学习】pytorch——线性回归
笔记为自我总结整理的学习笔记,若有错误欢迎指出哟~ 深度学习专栏链接: http://t.csdnimg.cn/dscW7 pytorch——线性回归 线性回归简介公式说明完整代码代码解释 线性回归简介 线性回归是一种用于建立特征和目标变量之间线性关系的统计学习方法。它假设…...

golang工程——中间件redis,单节点集群部署
单节点redis集群部署 部署redis 6.2.7版本 没资源,就用一台机子部 解压安装包 tar zxf redis-6.2.7.tar.gzcd redis-6.2.7编译安装 mkdir -p /var/local/redis-6.2.7/{data,conf,logs,pid}data:数据目录 conf:配置文件目录 logs…...

Lua基础
table 基本原理: table是一种特殊的容器,可以向数组一样按照索引存取,也能按照键值对存取。 local mytable {1,2,3} --相当于数组 local mytable {[1]1,[2]2,[3]3} --和上面等价 local mytable {1,2,3,[3] 4} --隐式赋值会覆盖掉显式赋…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...
