【tensorboard打开失败】No dashboards are active for the current data set.
这里我再跟视频学的时候，找了很多的指令，说是对应版本不一样，但是发现用了很多指令都可以弹出来跳转的url，那应该就不是输入指令的问题
直到我想把logs里面的文件删掉重新跑的时候，我突然注意到这里有中文字符，在联想起最下面的报错信息
那么我就把名字改了
随后我再次
tensorboard --logdir "logs"
就没再报编码错误的问题了，这样想下来应该是读取文件名出错，所以读不到文件，以至于页面说logs文件夹里没有文件的问题吧，所以注意生成文件不要有中文名就好了 （之前试用了用绝对路径，结果没注意文件夹里面文件的名字是中文的...）
相关文章：
【tensorboard打开失败】No dashboards are active for the current data set.
这里我再跟视频学的时候，找了很多的指令，说是对应版本不一样，但是发现用了很多指令都可以弹出来跳转的url，那应该就不是输入指令的问题 直到我想把logs里面的文件删掉重新跑的时候，我突然注意到这里有中文字符…...
客服管理者如何调动客服人员的积极性？
客户是企业的财富，良好的客户服务体验可以有效地促进企业的销售和声誉，因此，客服工作显得尤为重要。而客服人员的积极性直接影响了整个客服部门的质量和效率。如何调动客服人员的积极性，成为了每个客服管理者都需要面对的难题。本…...
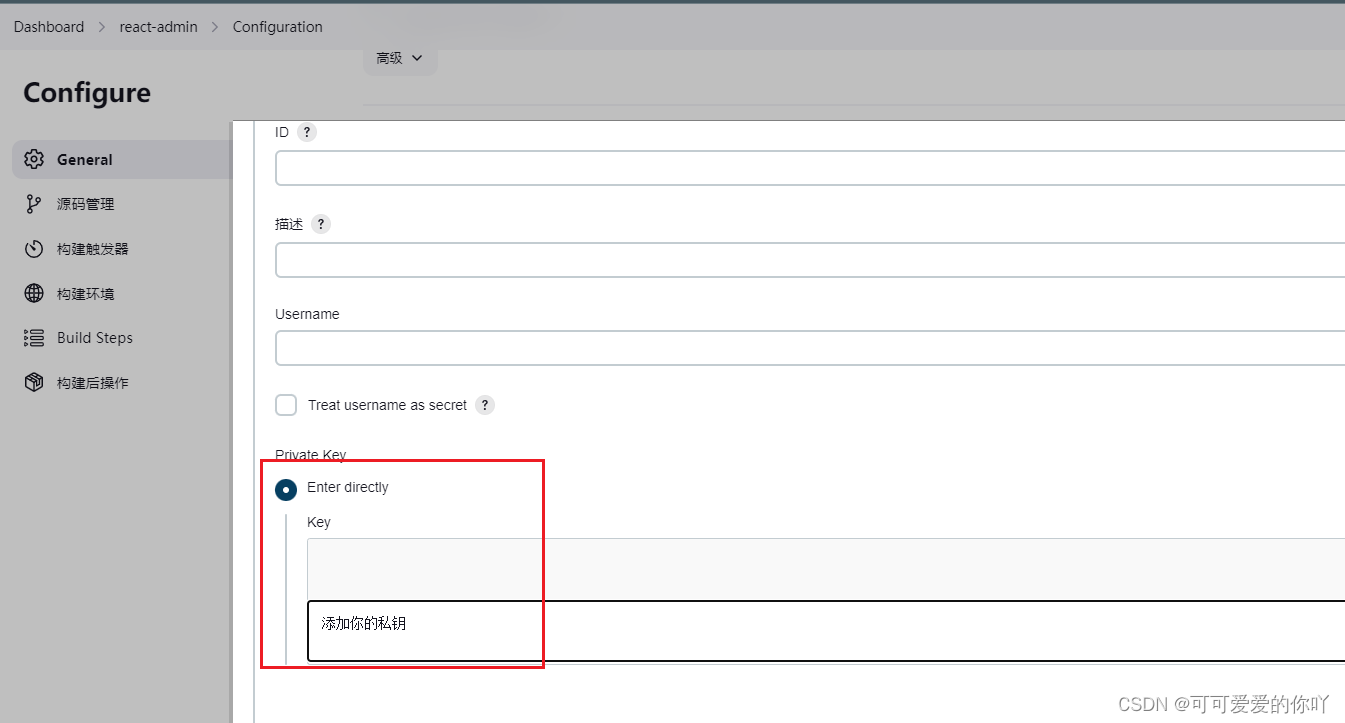
Jenkins自动化部署简单配置
下载安装jenkins 安装Jenkins步骤 点击Next的时候会有jdk版本跟Jenkins版本不符合的情况 1. 看下任务管理器内Jenkins服务是否启动，在浏览器里面输入localhost:2023（端口号是安装时输入的） 2. 根据路径找到放置密码的文件（C…...
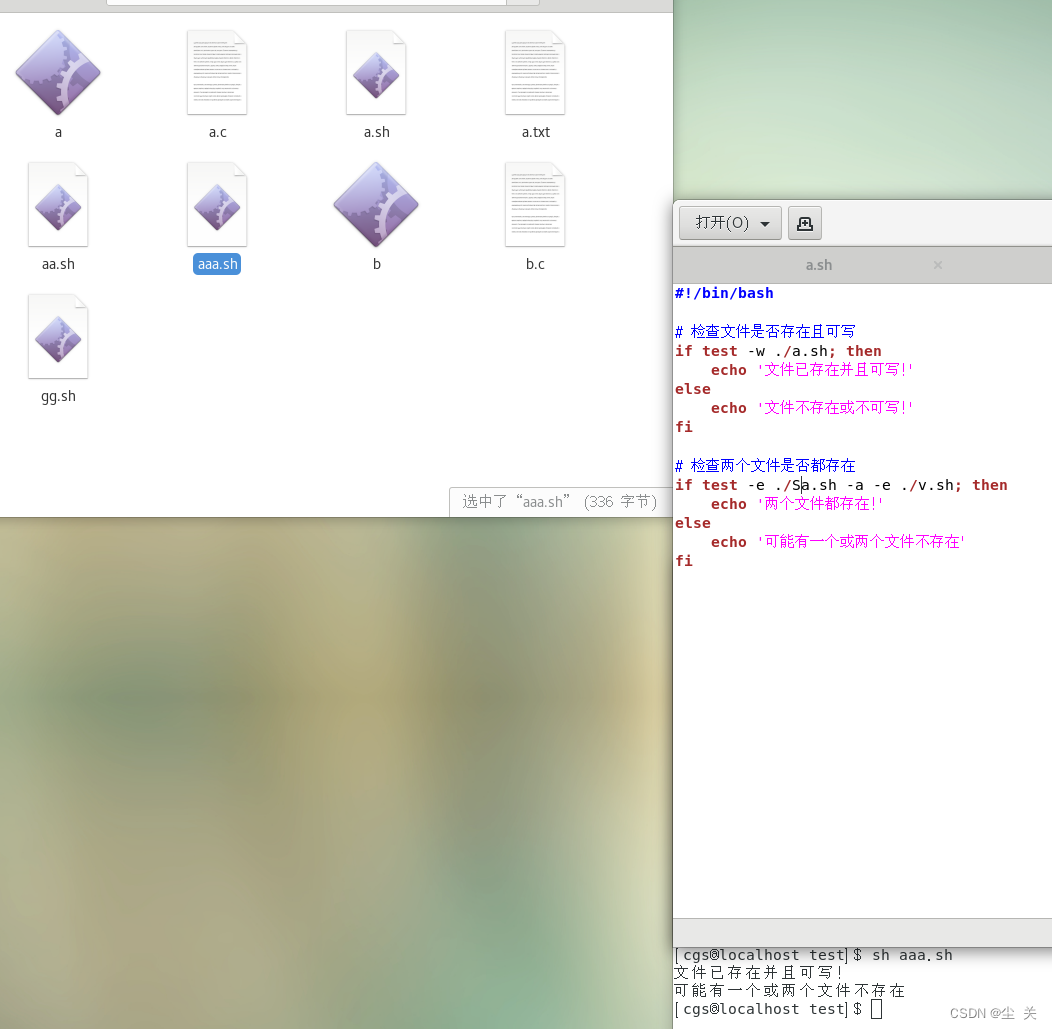
Linux————内置命令大全
（一）内置命令 Shell 内置命令，就是由 Bash Shell 自身提供的命令，而不是文件系统中的可执行脚本文件。内置命令的执行速度通常优于外部命令，因为执行外部命令不仅会导致磁盘I/O操作，而且还需要为其fork一个…...
从用户角度出发，如何优化大数据可视化体验｜北京蓝蓝UI设计公司
作者：蓝蓝设计-鹤鹤 大数据已经成为人们探索世界的新工具。但是，对于普通用户而言，大数据往往比较抽象和难以理解，因此，大数据可视化作为一种非常有效的工具工具被广泛应用。然而，在实际应用中，…...
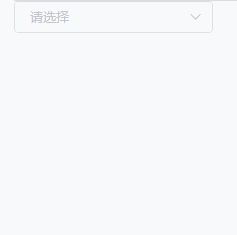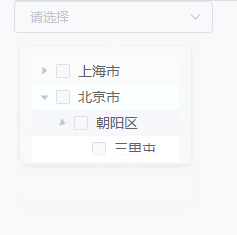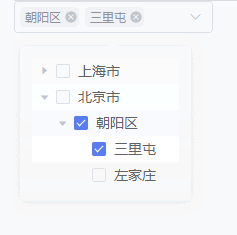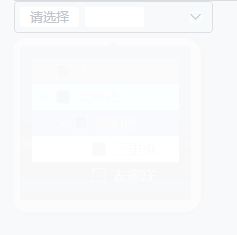
【vue】封装树形下拉框组件 el-popover+el-tree+el-select
父组件使用 <template><div>{{ array }} 更多属性详见wgyTreeSelect组件<wgyTreeSelectv-model"array":list"list":multiple"true":disabled-ids"[111,113,2]"/></div> </template><script> /*…...
docker安装Kafka，SpringBoot整合Kafka
#拉取镜像 docker pull wurstmeister/zookeeper #运行容器 docker run --restartalways --name zookeeper -p 2181:2181 \ -v /etc/localtime:/etc/localtime -d wurstmeister/zookeeper#拉取镜像 docker pull wurstmeister/kafka#运行容器 docker run --restartalways --name …...
MySQL - InnoDB 的事务支持、锁机制
InnoDB 存储引擎实现了强大的事务支持和锁机制： 事务原理： ACID 属性：InnoDB 支持 ACID（原子性、一致性、隔离性、持久性）属性，确保数据的一致性和可靠性。事务是一组 SQL 操作，要么全部执行&…...
Android Studio的笔记--Module新建和使用
Module新建和使用 新建module使用module android studio 中module的建立和使用。比如修改工程为module的步骤，引用module的步骤。 新建module 1、新建android工程，New Project.包名为com.lxh.serialport 2、修改工程为module。 2.1、在app下的build.pro…...
Git统计个人提交代码行数
目录 一、git bash打开二、查看个人提交的代码行数统计三、查看项目每个人提交的代码行数统计四、查询所有用户的提交总次数五、统计用户一段时间内的提交代码量 在实际开发中，常常会想查看自己对于某个项目的贡献，管理者会查看项目下各成员的贡献&#…...
Collction的List方法,list特有方法,遍历方式,迭代器选择
[to] list特有方法 //插入指定元素//list.add(1,"ddd");//System.out.println(list);//[aaa, ddd, bbb, ccc]//这个表示在一索引的位置插入ddd//他会把原来一索引位置的元素往后移动一位在添加//删除指定元素//String remove list.remove(1);//System.out.println(…...
奇偶校验码和循环冗余码
在数据链路层的传输中，1可能变成0，0可能变成1，这是比特差错。 为了应对比特差错，有两种方式，即自动重传请求ARQ（Automatic Repeat-reQuest）和前向纠错FEC（Forward Error Correction&…...
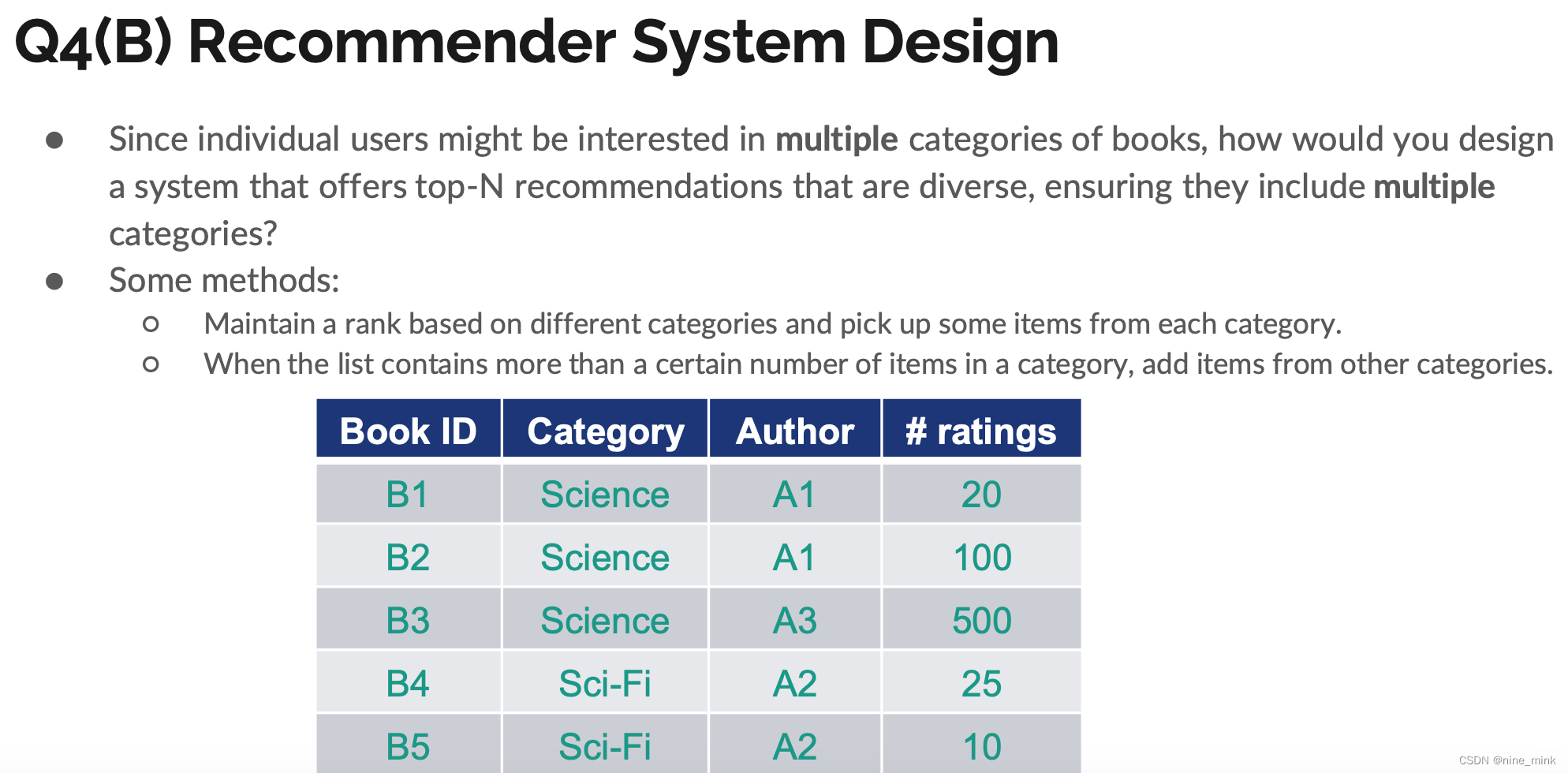
Recommender System复习（考试向）
Recommender System Review OverviewCollaborative Filtering基于用户的CF（User CF）基于物品的CF（Item CF）Similarity CalculationBias in CF Evaluation of Recommender SystemFactorization MachinesLatent factor modelLFM算法…...
SpringBoot绑定配置文件中变量的四种方式-解析
当在Spring Boot中需要绑定配置文件中的变量时，可以使用以下注解： PropertySource：用于指定要加载的属性文件。可以将该注解放置在Configuration类上。 Configuration PropertySource("classpath:application.properties") public…...
linux 安装 elasticsearch 全教程
一、去 elasticsearch官网找到Linux版本的下载链接 地址https://www.elastic.co/cn/downloads/elasticsearch 二、在linux 中用wget下载 wget https://artifacts.elastic.co/downloads/elasticsearch/elasticsearch-8.10.4-linux-x86_64.tar.gz三、下载成功后解压文件 tar -x…...
更快更准 | YOLOv3算法超详细解析（包括诞生背景+论文解析+技术原理等）
前言：Hello大家好，我是小哥谈。YOLOv3是一种基于深度学习的目标检测算法，它可以快速而准确地在图像中检测出多个目标。它是由Joseph Redmon和Ali Farhadi在2018年提出的，是YOLO（You Only Look Once）系列算法…...
 模式)
【ChatGPT】教我 Flyweight(享元) 模式
文章目录 设计模式中 Flyweight 模式，实际应用场景有哪些？我需要画很多的树，以这个需求为例来教我 Flyweight 模式。好的，我大概明白了，我还有点疑惑，请问外在状态和内在状态是哪些？你可以讲一下…...
双十一越来越早，公域电商何去何从——深度解析
为什么双十一越来越早？传统的公域电商越来越饱和,某淘某东甚至和某79元网红打起了价格战 ，市面上标品越来越多，商家越来越多，买东西的变少了，商家越卖越便宜。 公域电商： 就像一个大市场。里面摆满了各种商…...
区块链中的 “不可能三角，技术性ppt突出关键技术点，数据交易-安全问题
目录 区块链中的 "不可能三角 技术性ppt突出关键技术点 数据交易-安全问题...
[Docker]五.Docker中Dockerfile详解
Dockerfile 就是用来构建 docker 镜像的构建文件 1.Dockerfile 构建一个自己的 centos 镜像 新建一个名为 Dockerfile 文件，并在文件内添加以下内容: #基于centos构建镜像 FROM centos #安装net-tools软件: RUN表示安装软件 RUN yum install -y net-tools…...
【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现，玩家控制一个角色（龙）躲避障碍物（仙人掌和乌鸦）。以下是代码的详细介绍：…...
内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤： 1）请求大小调整：首先，malloc 需要调整用户请求的大小，以适应内部数据结构（例如，可能需要存储额外的元数据）。通常，这包括对齐调整，确保分配的内存地址满足特定硬件要求（如对齐到8字节或16字节边界）。 2）空闲…...
使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架，专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用，其中包含三个使用通用基本模板的页面。在此…...
ETLCloud可能遇到的问题有哪些？常见坑位解析
数据集成平台ETLCloud，主要用于支持数据的抽取（Extract）、转换（Transform）和加载（Load）过程。提供了一个简洁直观的界面，以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...
Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...
vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量，这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...
GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器（ADC），支持8kHz~96kHz采样率，集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器，适用于高保真音频采集场景。 2. 核心特性 高精度：24位分辨率，…...
10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI，使用客户端或是内部自己搭建集成大模型的终端，加速与大型语言模型（LLM）的结合，同时使用检索增强生成（Retrieval Augmented Generation &#…...
【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变（硬件篇）
本项目是基于 STM32F103C8T6 微控制器的 SPWM（正弦脉宽调制）电源模块，能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路，图中 D1 为二极管， 其目的是防止正负极电源反接， …...
在Mathematica中实现Newton-Raphson迭代的收敛时间算法（一般三次多项式）
考察一般的三次多项式，以r为参数： p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]； 此多项式的根为： 尽管看起来这个多项式是特殊的，其实一般的三次多项式都是可以通过线性变换化为这个形式…...