快速了解:什么是优化问题
1. 定义
数学优化问题是:在给定约束条件下,找到一个目标函数的最优解(最大值或最小值)。
2. 快速get理解
初学者对优化技术陌生的话,可以把 “求解优化问题” 理解为 “解一个不等式方程组”,解方程的。
以下我们用几个简单的例子来讲述什么是优化问题。
引用说明:下面的公式来自MindOpt新发布的基于大模型的AI工程师生成的内容截图,或者案例广场的案例里面的截图。
a. 比如一个鸡兔同笼问题:
有一笼兔子和鸡,兔子和鸡各有一个头,兔子有4只脚,鸡有两只脚。笼子上有 35 个头,下有94 个脚。请问兔子和鸡的数目各是多少?
对应的数学公式如下:

可以看到公式是两个 “等号 = ” 描写的约束关系的方程组。
这个时候算出来的结果是:
- 兔子的数量x=12
- 鸡的数量y=23
b. 而一个优化问题。 会增加不等式关系,然后增加了一个目标。比如上面的例子更改下:
有一笼兔子和鸡,兔子和鸡各有一个头,兔子有4只脚,鸡有两只脚。笼子上有头至少有30个,下面脚至多80个。要想兔子最多,请问最多有多少个兔子?
这个时候,对应的数学公式的约束就是个不等式的关系;另外,增加了个maximize x,也就是优化的目标。

这个时候,如果只考虑不等式的约束,解可能就是个域(有多种解、多个可行域)。
比如 x=1,y=29; x=3,y=29; x=3, y= 30……等等
增加了要将x最大化这个目标,就相当于在这个域里面找最大值。这个时候可以利用优化求解器进行计算,得出最优目标时候的变量取值,如下
- 兔子的数量 x=10,
- 鸡的数量y=20.
需要注意的是,在有些情况下,最优目标时的变量取值也有可能是个域(多解)的情况。
这里,是不是有高中学线性规划的感觉了?比如下面的高一题目,是不是很熟悉?
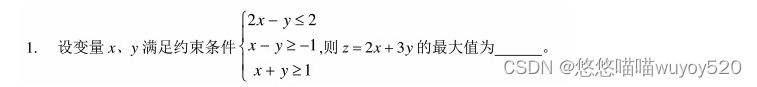
3. 拓展思路
3.1 拓展应用场景
在业务场景中使用优化的方法来描述业务遇到的问题。比如:
电商平台要为一家新兴手游公司进行广告推广,平台有两种广告类型可供选择:类型A、类型B、类型C。广告类型A的转化率为5%,每投放一次费用为10元;广告类型B的转化率为8%,每投放一次费用为15元; 广告类型B的转化率为7.7%,每投放一次费用为12元。手游公司需要至少获得1000次投放,并且总费用不能超过20000元。每种类型广告都希望至少投放5次。平台希望最大化累计转化数,要如何规划广告投放?
得到如下的优化问题数学公式:

最后用优化求解器算得的解是:
广告类型A投放次数=5
广告类型B投放次数=6
广告类型C投放次数=1655
目标函数值 = 128.165
3.2 拓展问题维度和类型
上面的问题都只有几个变量(未知数),还比较简单,如果有很多的变量呢,方程将很长,一般是用矩阵的方式来表达。比如:

也有用 大sigma 来表达求和∑的,比如下面几个金融投资里面应用的优化问题:

这里还关注下几个数学概念:
-
x * x,代表二次。优化问题里面常说的“线性”就是一次关系,y =3x就是一次的,线性关系。y = 4 x*x 就是二次的,属于非线性关系。
-
如果有的变量只能是整数,不能是小数,就是“离散的”。与之相对的是“连续的”。离散的问题优化起来会方法不一样,会变困难,因此经常有问题需要松弛下,使得变为连续的。
-
还有问题 “凸” 和 “非凸”。凸优化是个研究生课程,比较难。普通人需要掌握凸问题更好求解,非凸不好求解,因此列数学公式描述业务问题时,尽量避免非凸的情况。
4. 更丰富的优化问题类型列表
更进一步的,优化问题的数学模型根据不同的业务有很复杂的模型。基本就是要掌握好:可以控制的变量、不等式关系的约束、优化目标的情况。
不同的数学模型适合不同的场景,在优化问题计算的时候,也会有不同的复杂度。
常见的问题类型会以下的词汇来描述:
 | 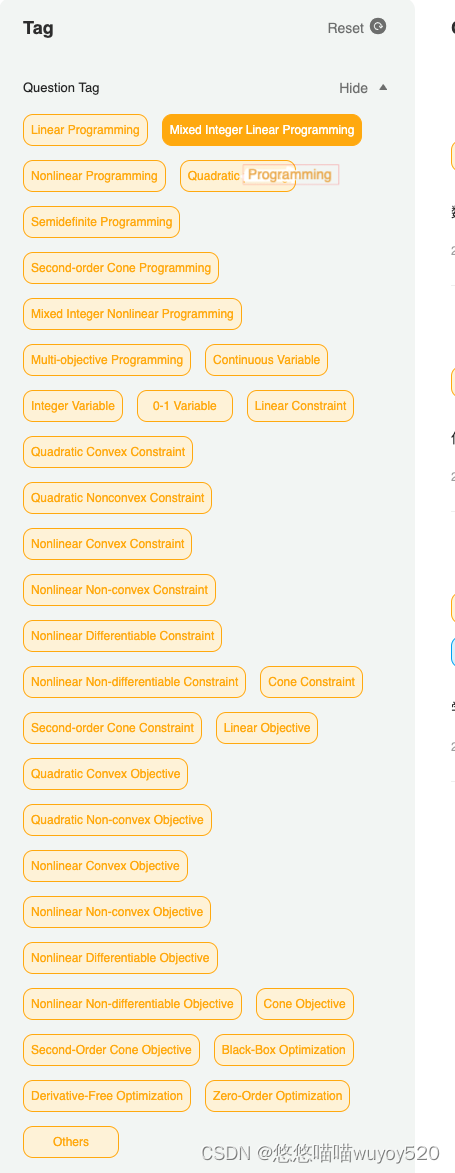 |
比如
- 线性规划,英文是Linear Programming,简称LP,对应的数说目标函数是线性关系。
- 如果加上变量有些是整数(integer),则组合成MILP(Mixed Integer Programming),混合整数的线性规划问题。
- 如果目标里面有二次项,则称为二次规划 QP(Quadratic Programming)。
- 如果约束里面有二次项,则称为二次约束规划 QC (Quadratic Constraint),组合还有QCQP
- 再进一步的根据目标约束的类型,还可以进一步分类描述不同类型的问题
- 再进一步,根据问题的优化计算方式,还可以取名字,比如零阶优化、黑盒优化等
类目很多,可遇到了后再查询标准术语。
4. 优化问题的应用
优化问题在运筹学、工程、经济学、物流、能源、金融等许多领域有应用。属于底层的数学技术, 应用面很广。在航空、航天、国防等也有应用。
对应的求解优化问题的优化求解器可以广泛应用于电力系统调度、生产计划、物流路径规划、投资组合优化等多个领域。使用优化求解器可以帮助用户更方便、更快速地找到问题的最优解。
推荐可以去阿里达摩院求解器的案例广场看看,了解应用场景,和对应的简单的数学模型、源代码。
5. 优化问题的计算
在实际业务里,一般情况下不太需要关心求解的方法,是借助工具来完成计算。更多地是需要了解不同算法计算的复杂度,是否能快速求解,如果不能,如何变更优化问题,使得能快速求解。
在选择或者研究求解器时,一般会评估如下特性:
- 是否能求解
- 求解速度
- 稳定性
- 大规模问题求解能力和计算资源占用
- 接口易用性
小编这里推荐去MindOpt的平台去看商用的和开源的求解器软件,从这个案例,复制项目进去用:https://opt.aliyun.com/example/vqaeimyI3iEj 。全程浏览器里面操作,不需要操心软件安装和License。
更多的优化软件,可以参考我之前的博客:https://blog.csdn.net/wuyoy520/article/details/134185148
相关文章:

快速了解:什么是优化问题
1. 定义 数学优化问题是:在给定约束条件下,找到一个目标函数的最优解(最大值或最小值)。 2. 快速get理解 初学者对优化技术陌生的话,可以把 “求解优化问题” 理解为 “解一个不等式方程组”,解方程的。…...
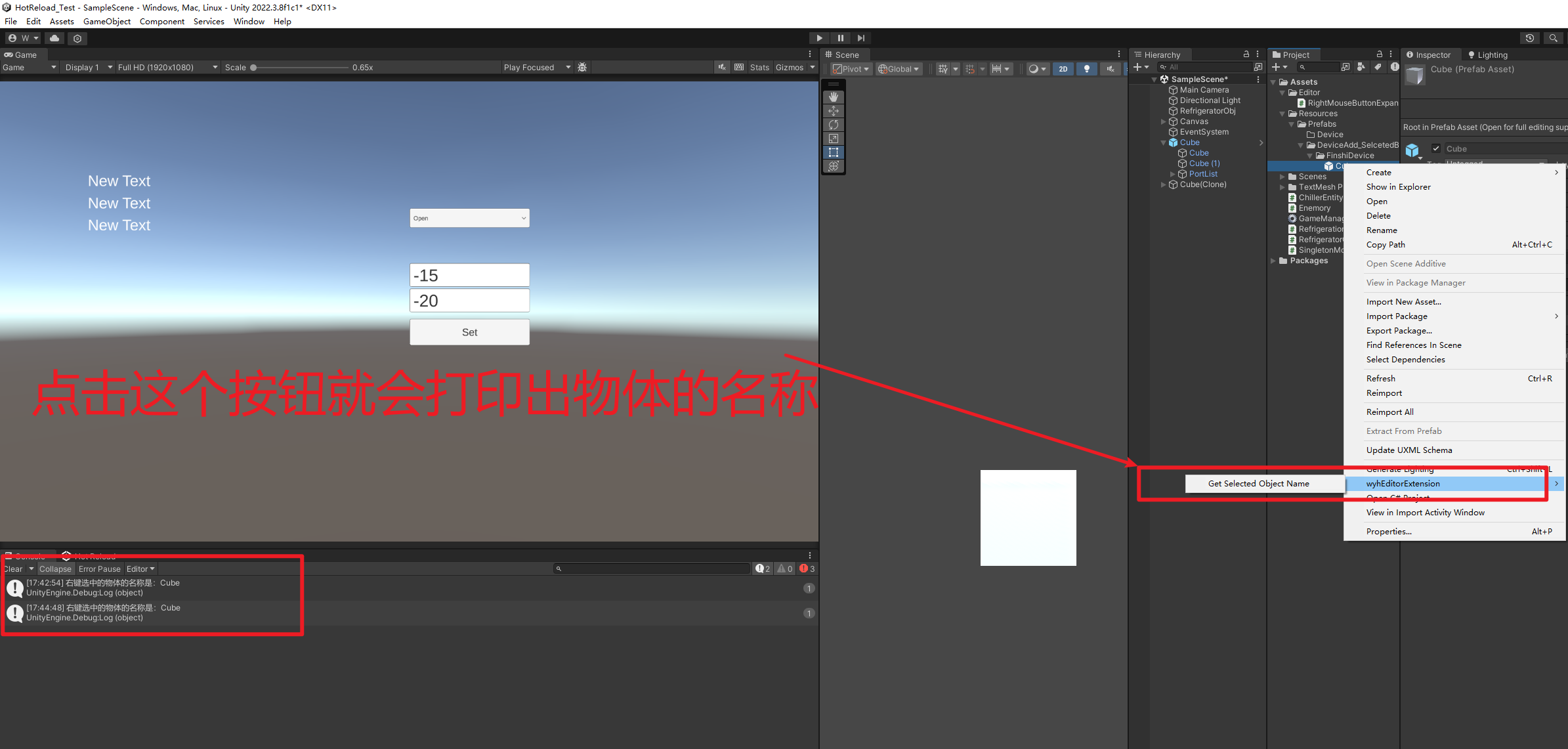
Unity在Project右键点击物体之后获取到点击物体的名称
Unity在Project右键点击物体之后获取到点击物体的名称 描述: 在Unity的Project右键点击物体之后选择对应的菜单选项点击之后打印出物体的名称 注意事项 如果获取到文件或者预制体需要传递objcet类型,然后使用 GameObject.Instantiate((GameObject)se…...
【带头学C++】----- 三、指针章 ---- 3.7 数组指针
3.7 数组指针 1.数组指针的概述 数组指针是一个指向数组的指针变量,是用来保存数组元素的地址。在C/C中,数组名代表了数组的首地址,可以被解释为一个指向数组第一个元素的指针。因此,一个指向数组的指针可以通过数组名来获…...

Ubuntu20.04安装CUDA、cuDNN、tensorflow2可行流程(症状:tensorflow2在RTX3090上运行卡住)
最近发现我之前在2080ti上运行好好的代码,结果在3090上运行会卡住很久,而且模型预测结果完全乱掉,于是被迫研究了一天怎么在Ubuntu20.04安装CUDA、cuDNN、tensorflow2。 1.安装CUDA(包括CUDA驱动和CUDA toolkit,注意此…...

untiy打开关闭浏览器
最简单的打开方法,只能打开不能关闭,自动打开默认浏览器 Application.OpenURL("https://www.bilibili.com/");打开关闭谷歌浏览器 using System.Diagnostics;private static Process web;if (web null)//打开 {web Process.Start("Chr…...

独立站优缺点解析,如何用黑科技进行缺点优化
随着跨境电商第三方平台平台红利越来越少,经营风险的不断增加,大部分人知道前年发生的亚马逊封店潮,涉及约1000家企业,5万多个账号,预估损失超过千亿元。 正因如此,更多的国内品牌和卖家不再仅依赖于第三方…...
道本科技||紧跟数字化转型趋势,企业如何提高合同管理能效?
随着数字化转型的快速发展,合同管理对于企业的运营效率和风险控制起着至关重要的作用。那么,如何紧跟数字化转型趋势,利用现代技术和工具提高合同管理的能效,以实现企业更高效、更安全的合同管理就成了企业管理中的核心问题。 在…...

框架安全-CVE 复现Apache ShiroApache Solr漏洞复现
文章目录 服务攻防-框架安全&CVE 复现&Apache Shiro&Apache Solr漏洞复现中间件列表常见开发框架Apache Shiro-组件框架安全暴露的安全问题漏洞复现Apache Shiro认证绕过漏洞(CVE-2020-1957)CVE-2020-11989验证绕过漏洞CVE_2016_4437 Shiro-…...
【OpenCV实现图像梯度,Canny边缘检测】
文章目录 概要图像梯度Canny边缘检测小结 概要 OpenCV中,可以使用各种函数实现图像梯度和Canny边缘检测,这些操作对于图像处理和分析非常重要。 图像梯度通常用于寻找图像中的边缘和轮廓。在OpenCV中,可以使用cv2.Sobel()函数计算图像的梯度…...

Spring Boot 解决跨域问题的 5种方案
跨域问题本质是浏览器的一种保护机制,它的初衷是为了保证用户的安全,防止恶意网站窃取数据。 一、跨域三种情况 在请求时,如果出现了以下情况中的任意一种,那么它就是跨域请求: 协议不同,如 http 和 https…...

linux 3.13版本nvme驱动阅读记录一
内核版本较低的nvme驱动代码不多,而且使用的是单队列的架构,阅读起来会轻松一点。 这个版本涉及到的nvme驱动源码文件一共就4个,两个nvme.h文件,分别在include/linux ,include/uapi/linux目录下,nvme-core.c是主要源码…...

掌握RESTful API:规范与设计详解
前言 RAML (RESTful API Modeling Language) 和 OAS (OpenAPI Specification) 都是用于描述和定义 RESTful API 的规范。它们分别提供了不同的功能和优势。 RAML(RESTful API Modeling Language): RAML简介 RAML(RESTful API M…...
「更新」Topaz Video AI v4.0.3中文版
Topaz Video AI是一款功能强大的视频处理软件,它利用人工智能技术对视频进行智能分析和优化,旨在为用户提供高效、智能的视频编辑和增强功能。 首先,Topaz Video AI具备强大的视频修复功能。它可以自动识别并修复视频中的各种问题࿰…...

OpenAI最新官方GPT最佳实践指南,一文讲清ChatGPT的Prompt玩法
原文:Sina Visitor System OpenAI的官网发表万字GPT最佳实践指南,讲清Prompt提示词的原则和策略,这里是总结和全文翻译 原创图像,AI辅助生成 OpenAI的官网上刚刚发表一篇万字的GPT最佳实践指南,这份指南把写好Promp…...
树结构及其算法-用链表来实现二叉树
目录 树结构及其算法-用链表来实现二叉树 C代码 树结构及其算法-用链表来实现二叉树 以链表实现二叉树就是使用链表来存储二叉树,也就是运用动态分配内存和指针的方式来建立二叉树。 使用链表来表示二叉树的好处是节点的增加与删除操作相当容易,缺点…...
:在hostapd获取已关联的STA的MAC地址)
openwrt(三):在hostapd获取已关联的STA的MAC地址
在深度开发openwrt的hostapd模块的时候,有些功能的实现需要获取已关联的sta的mac地址,下面是相关的方法描述: 第一、在sta_info.c文件中,可以找到一个名为struct hostap_sta_info * hostapd_get_sta(struct hostapd_data *hapd, …...

为何袁世凯要把“元宵节”改为“上元节”?
网民把春节除夕日排除在法定假期之外的相关热议,在微博评论区部分已被关闭。官方学者的解释是:“回归传统。” 这就令人难免要回顾历史,并发觉只有在袁世凯称帝之后,才有过取消“元宵节”改为“上元节”的笑话,因为“元…...
python将图片序列保存成gif
这里用到的模块是imageio。用imageio.mimsave即可将图片序列保存成gif动态图。以下是本人编写的小实验: import cv2 import imageiopaths ["./images/0001.png", "./images/0002.png", "./images/0003.png", ...] frames [] for i…...

UE4用C++修改蓝图对象的属性值
if (auto Property FindFProperty<FStrProperty>(Class, "A")){Object->Modify();Property->SetPropertyValue_InContainer(Object.GetClass(), "OK");}...

供应商等级:一级、二级和三级供应商之间有什么区别
作为一名专业采购人员,你知道拥有一个可靠且具有成本效益的供应链有多么重要。确保供应链顺利运行的方法之一就是利用供应商分级。 什么是供应商分级? 供应商分级是根据供应商的绩效和对企业的重要性,对其进行分类的做法。 因此,…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...
