虹科荣誉 | 喜讯!虹科成功入选“广州首届百家新锐企业”!!
文章来源:虹科品牌部
阅读原文:虹科荣誉 | 喜讯!虹科成功入选“广州首届百家新锐企业”!!
近日,由中共广州市委统战部、广州市工商业联合会、广州市工业和信息化局、广州市人民政府国有资产监督管理委员会、广州市科学技术局联合开展的“广州首届百家新锐企业培优计划”评选企业名单正式出炉。虹科凭借优秀的研发创新能力、企业综合实力及未来发展潜力在众多优秀企业中脱颖而出,成功入选“广州首届百家新锐企业”!


关于广州首届百家新锐企业
本次“广州首届百家新锐企业”榜单针对营收在1000万到2亿之间民营企业开展选拔培育。主要是在新一代信息技术领域、半导体及集成电路领域、智能制造领域、生物医药与健康领域、新能源新材料领域等5个战略性产业链中挖掘培育100家创新型、成长型民营企业。同时,该计划旨在团结、服务、教育和引导好新锐民营企业家按照新发展理念谋划推进企业改革发展,更好发挥国有、民营龙头企业带动作用,培育和扶持一批创新型、成长型民营企业发展壮大,促进产业链上中下游、大中小企业融通创新。
该计划五部门联动,拟打造成为广州的一张名片。入选后政府将有多项支持,包括但不限于给予更多关注、提供更多机会、链接各方资源为新锐企业成长助力赋能。
虹科能够成功入选“广州首届百家新锐企业”,离不开我们在行业内二十余年的辛勤耕耘,积累了所在领域大量前沿的高端技术和知识经验,获得了市场和行业广泛认可。同时,创新一直是虹科发展的第一驱动力,近年来虹科不断加大研发投入与人才储备力度,为持续的创新能力打下坚实基础,通过科技创新提高产业效率,通过创新帮助客户成功是我们矢志不渝的使命。
虹科始终坚持“专业专注、创新创造”的理念,以市场需求和技术创新双轮驱动发展,不断探索先进技术,未来,虹科将继续积极响应创新驱动发展战略,持续提升科技创新能力,共创科技未来。
——虹科,您可靠的解决方案合作伙伴!
广州虹科电子科技有限公司(前身是宏科)成立于1995年,总部位于中国南方经济和文化中心-广州,是国家高新技术企业、国家“专精特新”小巨人企业、广东省守合同重信用企业、广州市纳税A级企业、广州开发区瞪羚企业。

虹科是一家备受瞩目的高科技解决方案合作伙伴,致力于通过创新帮助客户成功。作为行业领军者,在工业和制造业的自动化和数字化、汽车研发测试、自动驾驶、医疗环境及运输监测、生命科学、机器视觉、云计算、工业物联网、5G、网络安全、工业AR、光电、仿真测试等诸多领域开拓出一片新天地。凭借60项+专利,我们掌握着行业前沿的技术和创新力量,服务的知名客户超8000家。
未来,虹科将继续秉持创新精神,不断探索业务的创新模式和发展路径,我们将建设更加专业的人才队伍和研发专线,将助力客户成功作为我们的核心服务宗旨,成为本土可靠的高科技解决方案合作伙伴!
相关文章:

虹科荣誉 | 喜讯!虹科成功入选“广州首届百家新锐企业”!!
文章来源:虹科品牌部 阅读原文:虹科荣誉 | 喜讯!虹科成功入选“广州首届百家新锐企业”!! 近日,由中共广州市委统战部、广州市工商业联合会、广州市工业和信息化局、广州市人民政府国有资产监督管理委员会…...

如何利用Jmeter从0到1做一次完整的压测?这2个步骤很关键!
压测,在很多项目中都有应用,是测试小伙伴必备的一项基本技能,刚好最近接手了一个小游戏的压测任务,一轮压测下来,颇有收获,赶紧记录下来,与大家分享一下,希望大家能少踩坑。 一、压…...
_2023)
基于STM32+微信小程序设计的智能门锁(4种开锁方式)_2023
一、项目介绍 1.1 项目背景 随着智能家居的普及,智能门锁作为一个非常重要的组成部分,受到了人们越来越多的关注。传统的机械锁门禁已经不能满足人们对于门锁安全、便捷性和智能化的需求,因此市场对于智能门锁的需求不断增加。而随着技术的发展,基于单片机的智能门锁已经…...

享受户外的美好时光:花园吊椅的魅力
拥有舒适的花园吊椅,就像在家中创造了一个度假天堂。这些轻松摇摆的座位为您提供了一个完美的地方,既能舒适躺卧,又能让您在家中的花园或庭院中感受到度假的氛围。度过美好时光的吊椅,将成为家庭花园的一大亮点,为您带…...

游戏中找不到d3dx9_43.dll怎么办,教你快速解决方法
在计算机的世界里,我们经常会遇到一些让人头疼的问题。比如,有一天,小明正在玩他最喜欢的游戏,突然弹出了一个错误提示:“由于找不到d3dx9_43.dll,无法继续执行代码”。小明感到非常困惑,不知道这是什么意思…...

蓝桥杯:买不到的数目
对于两个互质的正整数 n , m n,m n,m,请找出来不能被 n n n和 m m m组成的最大数 X X X 例如:对于4,7那么 X X X17,因为对于大于17的任一数都可由4和7组成。 重新翻译题目: 对于任一大于 X X X的正整数 Y Y Y满足 Y a n b m Y a \times nb \times m …...
Nginx简介,Nginx搭载负载均衡以及Nginx部署前端项目
目录 一. Nginx简介 Nginx的优点 二. Nginx搭载负载均衡 2.1 Nginx安装 2.1.1 安装依赖 2.1.2 解压nginx安装包 2.1.3 安装nginx 2.1.4 启动nginx服务 2.2 tomcat负载均衡 2.3 Nginx配置 三. Nginx前端部署 一. Nginx简介 NGINX(读作:engi…...
QT5.15.2搭建Android编译环境及使用模拟器调试(全)
一、安装QT5.15.2 地址:下载 我电脑的windows的,所以选windows 由于官方安装过程非常非常慢,一定要跟着步骤来安装,不然慢到怀疑人生 1)打开"命令提示符"(开始 -> Windows 系统 -> 命令…...

npm install报 ERESOLVE unable to resolve dependency tree
三四年前的一个项目,打开,npm install 一下,结果报 ERESOLVE unable to resolve dependency tree。 以前install都一切顺利,现在就不行,那很大的可能是npm的版本不同。 PS D:\workSpace\code\*-admin-ui-master> n…...

CentOS 7上创建Python 3虚拟环境
在CentOS 7上创建Python 3虚拟环境可以使用virtualenv包。以下是创建Python 3虚拟环境的步骤: 确保已经安装了Python 3和pip。可以通过在终端中运行以下命令来检查它们是否已安装: python3 --version pip3 --version如果未安装,请使用以下…...
B端设计必看的9个开源组件库,值得收藏!
如果你想开发一款To B Web端产品,如何选择令人眼花缭乱的开源组件库?行业团队常用的B端开源组件库是什么?今天,我们将为您带来入门级开源组件库的介绍。你可以先有一个大致的了解,希望能对你有所帮助。未来,…...

王坚院士:云计算与 GPT 的关系,就是电和电动机的关系
无论是行业,还是阿里,都身处巨变时。已经年过六十的王坚院士,重回阿里,重回大众视野,今年以来,在多个场合都能够看到他的身影。 而每一次他的分享,都值得我们细细品味。 以下为王坚院士在 202…...
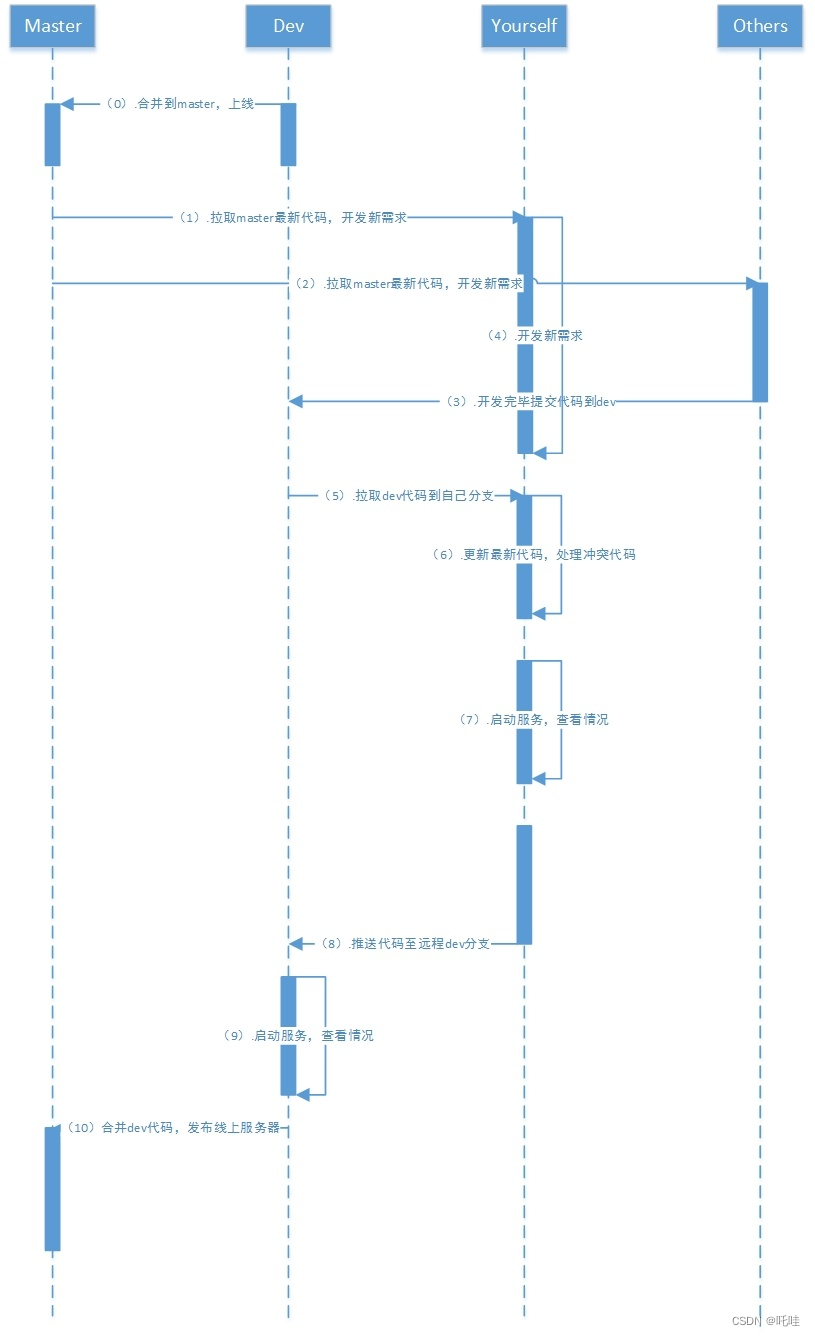
Git代码合并流程规范
...

编译cef114.2 with h264
按照下面网页要求安装VS和SDK https://bitbucket.org/chromiumembedded/cef/wiki/BranchesAndBuilding.md#markdown-header-development Win 10 deployment, Win 10 build system w/ VS2022 17.5, Win 10.0.22621 SDK, Ninja rem 配置winsock科学上网 netsh winhttp set prox…...
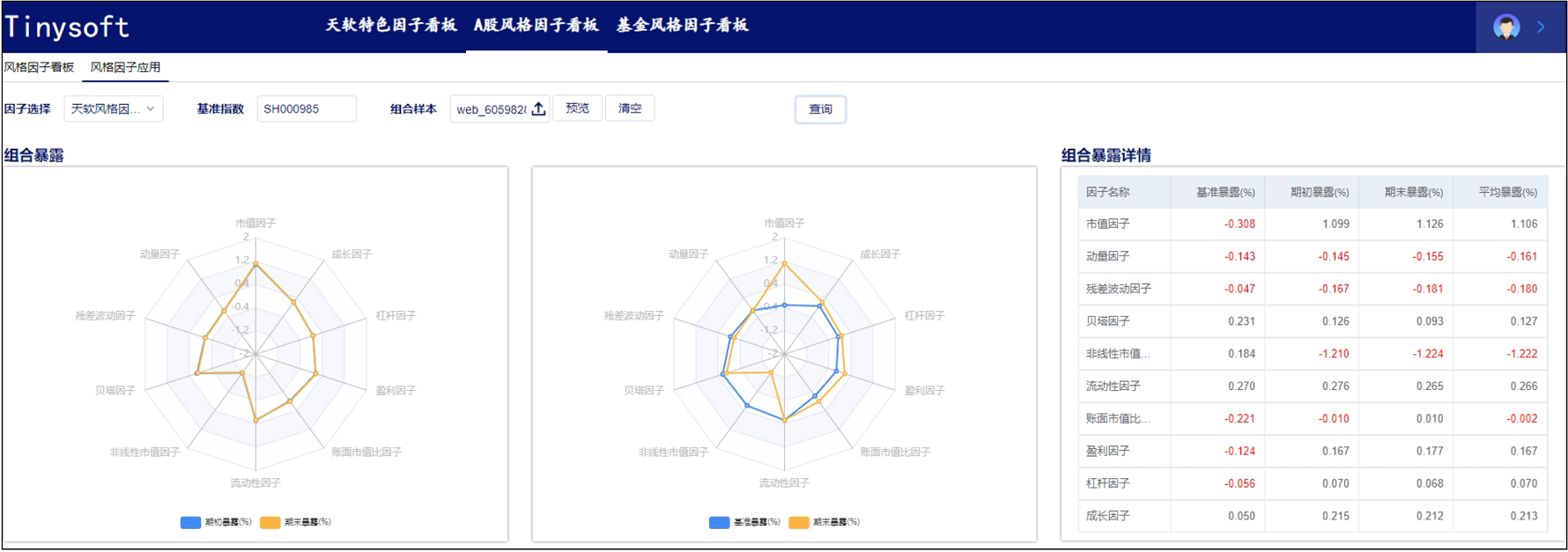
A股风格因子看板 (2023.11第01期)
该因子看板跟踪A股风格因子,该因子主要解释沪深两市的市场收益、刻画市场风格趋势的系列风格因子,用以分析市场风格切换、组合风格暴露等。 今日为该因子跟踪第01期,指数组合数据截止日2023-10-31,要点如下 近1年A股风格因子收益走…...

Session+Cookie实现登录认证
使用 Session 和 Cookie 实现登录认证的流程通常包括以下步骤: 1. 登录认证流程 用户登录: 用户在登录页面输入用户名和密码。 服务器验证用户的凭证(用户名和密码)是否正确。 创建会话(Session)…...
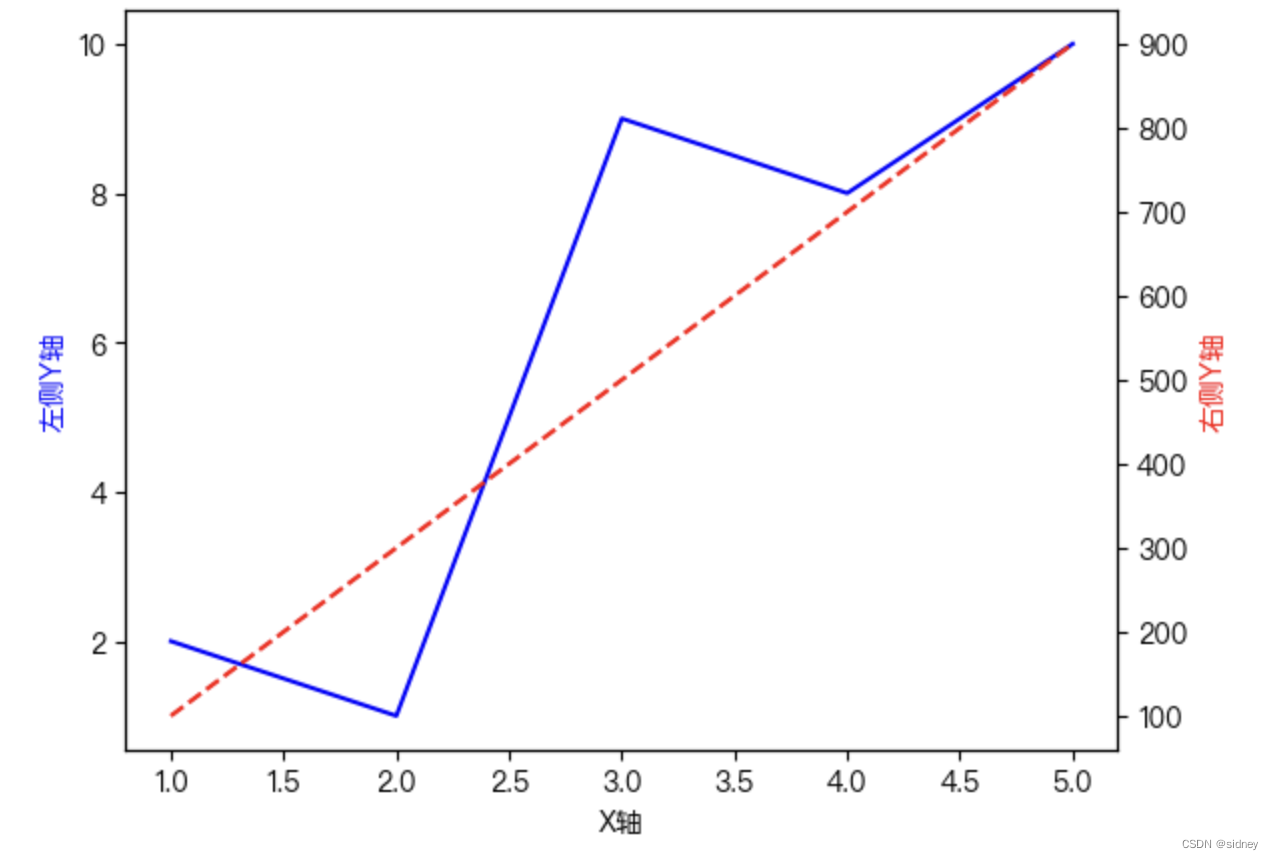
mac matplotlib显示中文
以下默认字体,在mac ventura上测试能成功显示中文: import matplotlib.pyplot as plt import matplotlib#from matplotlib import font_manager #plt.rcParams[font.sans-serif] [Heiti TC]#plt.rcParams[font.sans-serif] [Songti SC]#plt.rcParams[f…...
python自动化测试模板
1:准备html模版 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 <!DOCTYPE html> <html> <head> <meta charset"utf-8"> <title>接口自动化…...

MySQL 外连接和内连接的查询优化怎么做?
目录 1. 表连接方式的分类和需要注意的细节 2. 表连接时底层做了什么事? 3. 左外连接优化方案 4. 内连接优化方案 1. 表连接方式的分类和需要注意的细节 多表连接查询,大体上可以分为内连接与外连接。 内连接的意思就是把两个表有关联的部分都取出…...
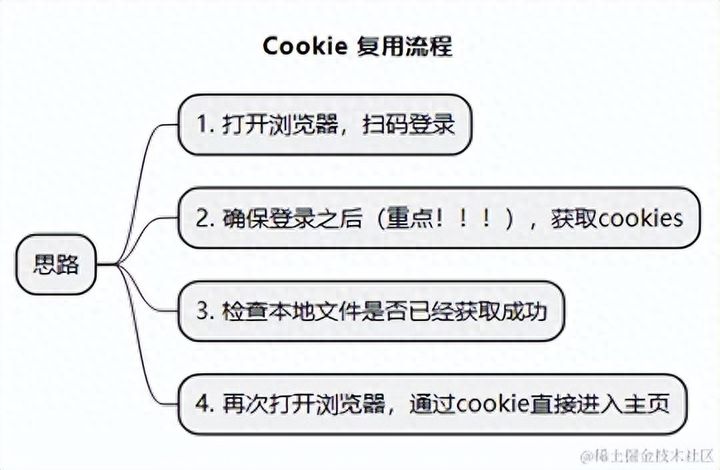
Web自动化测试 —— cookie复用
一、cookie简介 cookie是一些数据,存储于用户电脑的文本文件中 当web服务器想浏览器发送web页面时,在链接关闭后,服务端不会记录用户信息 二、为什么要使用Cookie自动化登录 复用浏览器仍然在每次用例开始都需要人为介入若用例需要经常执行&…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...
