蓝桥杯 (C++ 求和 等差数列 顺子日期 灌溉)
目录
1、求和
题目:
思路:
代码:
2、等差数列
题目:
思路:
代码:
3、顺子日期
题目:
思路:
代码:
4、灌溉
题目:
代码:
1、求和
题目:

思路:
1、首先想到的是两重遍历,累加和。但是当n取200000时,会超时,所以暴力的遍历没有办法通过全部案例。
2、将公式变形得到S=a1*(a2+....+an)+a2*(a3+....+an)+.....+an.
3、所以先求所有项的累加和sum,从第一项开始每次将sum减去一项自身ai乘以自身ai,再将这些和相加得到结果。
代码:
#include<iostream>
using namespace std;
int main()
{int n,a[200010];cin >> n;long long sum = 0;for (int i = 0; i < n; i++){cin >> a[i];sum += a[i];}long long ans = 0;for (int i = 0; i < n; i++){sum -= a[i];ans += a[i] * sum;}cout << ans;
}2、等差数列
题目:

思路:
1、求等差数列,一开始想到直接找它们的最小差作为公差,但实际上是不行的,这可能没有办法构成等差数列。(比如:15、5、1这三个数,如果取5-1的差4为公差,会发现1、5、9、13、17,15不在等差数列中,所以不可取。)
2、通过上面的例子我们可以发现,我们要求的公差是可以满足一个数可以等于从另一个数加公差的倍数。所以我们要求的公差,是将所有数从小到大排序,所有相邻两数差的最大公约数。(比如:1、5、15,差有4、10,它们的最大公约数为2,所以公差为2,构成1、3、5、7、9、11、13、15的等差数列。)
3、最后得到公差,个数即位最大的数减去最小的数/公差+1;有一种情况比较特殊,当公差为0,即每个数都相等的时候,个数即为n。
代码:
#include<iostream>
#include<algorithm>
using namespace std;
long long gcd(int a, int b)//辗转相除,求最大公约数
{if (b == 0)return a;elsereturn gcd(b, a % b);
}
int main()
{int n;cin >> n;long long a[100010];for (int i = 0; i < n; i++)cin >> a[i];sort(a, a + n);long long d = a[1] - a[0];for (int i = 2; i < n; i++){d = gcd(d, a[i] - a[i - 1]);}if (a[n - 1] == a[0])cout << n;elsecout << ((a[n - 1] - a[0]) / d )+ 1;
}3、顺子日期
题目:

思路:
1、判断每一天是否存在顺子序列:012、123、234.......,只要存在一个顺子序列即为顺子日期。
代码:
#include<iostream>
#include<algorithm>
using namespace std;
int judge(int t[])
{int flag = 0;for (int i = 3; i <= 5; i++){if (t[i] == (t[i + 1] - 1) && (t[i + 1] == t[i + 2] - 1)){flag = 1;break;}}return flag;
}
int main()
{int day[13] = { 0,31,28,31,30,31,30,31,31,30,31,30,31 };int t[8] = { 2,0,2,2 },ans = 0;for (int i = 1; i <= 12; i++){t[4] = i / 10;t[5] = i % 10;for (int j = 1; j <= day[i]; j++){t[6] = j / 10;t[7] = j % 10;if (judge(t)){ans++;//for (int i = 0; i < 8; i++)//cout << t[i];//cout << endl;}}}cout << ans;
}4、灌溉
题目:

代码:
#include<iostream>
#include<cmath>
using namespace std;
int n, m, t, r[110], c[110];
int main()
{cin >> n >> m >> t;for (int i = 1; i <= t; i++)cin >> r[i] >> c[i];int k;cin >> k;int cnt = 0;for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){for (int l = 1; l <= t; l++){int d = abs(r[l] - i) + abs(c[l] - j);if (d <= k){cnt++;break;}}}}cout << cnt << endl;
}相关文章:

蓝桥杯 (C++ 求和 等差数列 顺子日期 灌溉)
目录 1、求和 题目: 思路: 代码: 2、等差数列 题目: 思路: 代码: 3、顺子日期 题目: 思路: 代码: 4、灌溉 题目: 代码: 1、求和…...

Spring AOP基于XML方式笔记整理
XML AOP 加载流程 ClassPathXmlApplicationContext#refreshAbstractApplicationContext#obtainFreshBeanFactoryAbstractRefreshableApplicationContext#refreshBeanFactory创建DefaultListableBeanFactoryAbstractApplicationContext#loadBeanDefinitions(beanFactory)创建Xm…...
 Proxy代理方式连接互联网)
Docker HTTP(S) Proxy代理方式连接互联网
Docker HTTP(S) Proxy 是一种在 Docker 容器内部设置 HTTP(S) 代理的方法,以便于容器内的应用程序可以方便地通过代理访问互联网。设置 HTTP(S) 代理的方法主要有两种:使用 Dockerfile 配置和在使用 docker run 时添加参数。 以下是使用 Docker HTTP(S) …...
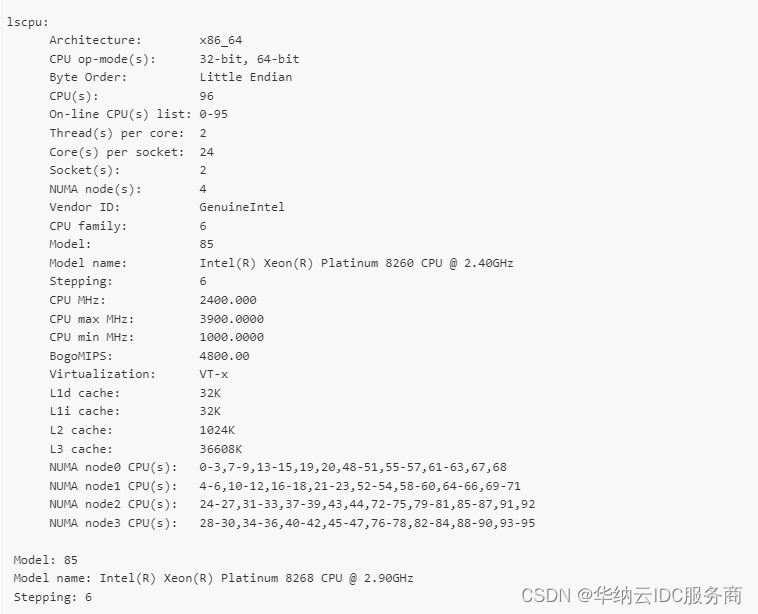
华纳云:centos系统中怎么查看cpu信息?
在CentOS系统中,我们可以使用一些命令来查看CPU的详细信息。下面介绍几个常用的命令: 1. lscpu lscpu命令可以显示CPU的架构、型号、核心数、线程数、频率等信息。 # lscpu 执行以上命令后,会输出类似以下内容: 2. cat /proc/…...

如何选择微信管理系统?
如何选择微信管理系统? 1、不用下载安装软件,不越狱不刷机 2、不绑定手机或电脑,不对电脑或手机做限制,也不受电脑、手机关闭、关机影响 3、能更新迭代,不限制版本 4、使用安全登录,保障账号安全的 5、不用…...

文字的力量
不知道以前的时代的年轻人有没有这样的感受。现在我觉得自己是不是出现了认知偏差,发现在很多描写现在的二十几岁年轻人的成长经历的文字下面都会出现很多共鸣,包括我自己也有,就让我有一个错觉:是不是中国所有的和我同龄的年轻人都是这样过来…...

荒野大镖客emp.dll文件丢失的怎么办,快速修复游戏dll问题
在玩荒野大镖客这款游戏的过程中,我遇到了一个令人困扰的问题——emp.dll文件丢失。emp.dll是荒野大镖客游戏中的一个动态链接库文件,它负责管理游戏中的一些功能模块。当这个文件丢失时,游戏可能无法正常运行,导致一些功能无法使…...

力扣labuladong——一刷day20
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言差分数组工具类一、力扣370. 区间加法二、力扣1109. 航班预订统计三、力扣1094. 拼车 前言 差分数组的主要适用场景是频繁对原始数组的某个区间的元素进行增减…...
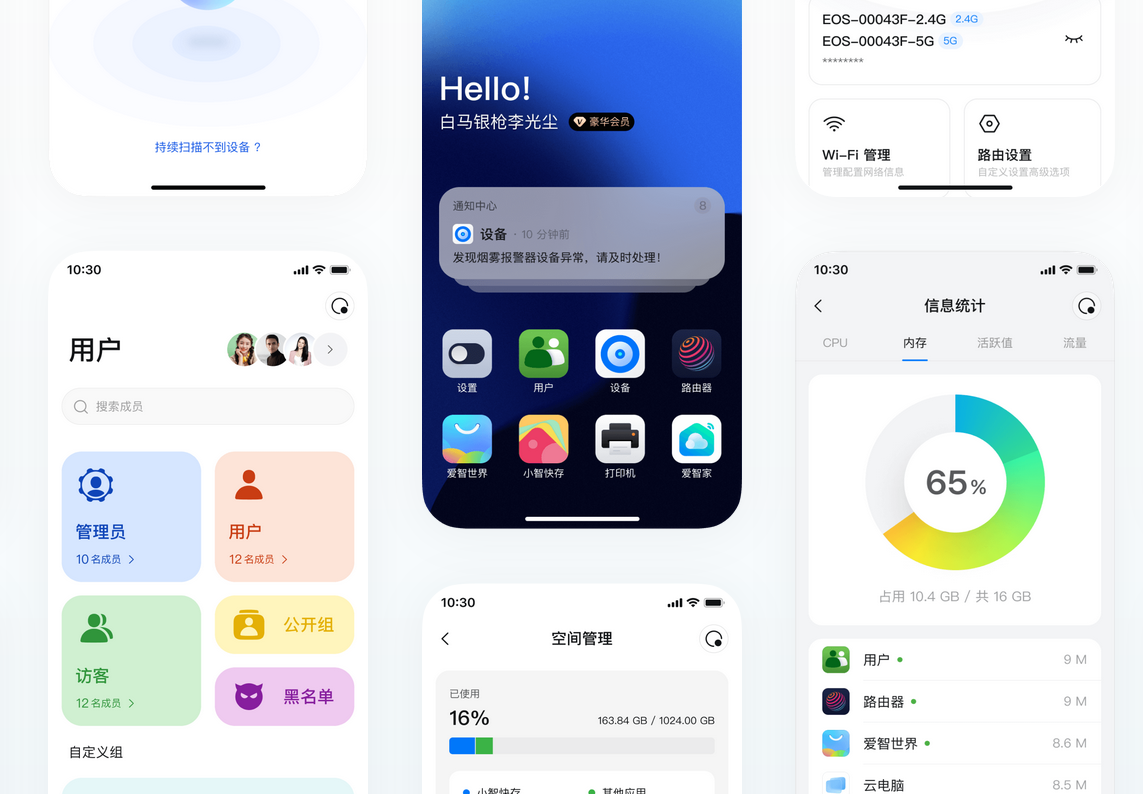
XSpirit 2智能边缘计算机使用测评
博客主页:https://tomcat.blog.csdn.net 博主昵称:农民工老王 主要领域:Java、Linux、K8S 期待大家的关注💖点赞👍收藏⭐留言💬 目录 拆箱过程介绍视频使用感受 我之前就参加过 Spirit 1 第一代智能边缘计…...

python实现MC协议(SLMP 3E帧)的TCP服务端(篇二)
python实现MC协议(SLMP 3E帧)的TCP服务端是一件稍微麻烦点的事情。它不像modbusTCP那样,可以使用现成的pymodbus模块去实现。但是,我们可以根据协议帧进行组包,自己去实现帧的格式,而这一切可以基于socket模…...
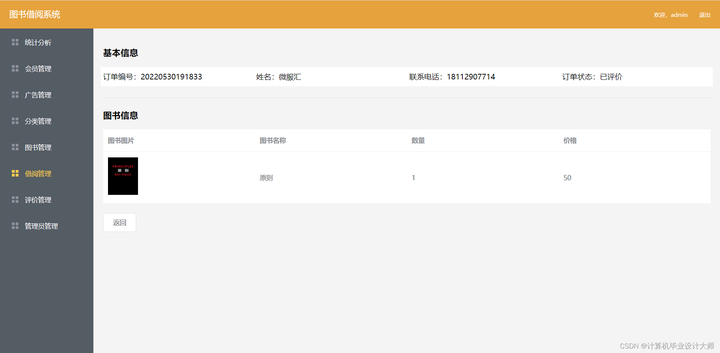
nodejs express uniapp 图书借阅管理系统源码
开发环境及工具: nodejs,mysql5.7,HBuilder X,vscode(webstorm) 技术说明: nodejs express vue elementui uniapp 功能介绍: 用户端: 登录注册 首页显示轮播图&am…...

从零开始的目标检测和关键点检测(一):用labelme标注数据集
从零开始的目标检测和关键点检测(一):用labelme标注数据集 1、可视化标注结果2、划分数据集3、Lableme2COCO,将json文件转换为MS COCO格式 前言:前段时间用到了mmlab的mmdetction和mmpose,因此以一个小的数…...
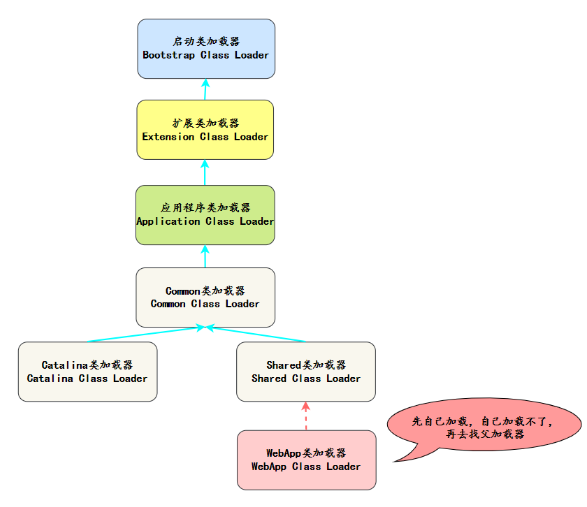
【JVM经典面试题(五十二道)】
文章目录 JVM经典面试题(五十二道)引言1.什么是JVM 内存管理2.能说一下JVM的内存区域吗?3.说一下JDK1.6、1.7、1.8内存区域的变化?4.为什么使用元空间替代永久代作为方法区的实现?5.对象创建的过程了解吗?6…...
高效管理:在文件夹名称左边添加关键字,实现批量重命名
在高效的文件管理中,对文件夹进行合理命名和重命名是十分关键的。有时候,我们可能需要在一批文件夹的名称左边添加特定的关键字,以便更好地组织和管理这些文件夹。为了实现这个目标,我们可以使用云炫文件管理器一些简单的步骤来实…...
Leetcode1122. 数组的相对排序
Every day a Leetcode 题目来源:1122. 数组的相对排序 解法1:哈希 用集合 set 存储 arr2 中的元素。 遍历数组 arr1 ,设当前元素为 num: 如果 num 在 set 中出现,用哈希表 hash 记录 num 和它出现的次数。否则&a…...

CN考研真题知识点二轮归纳(5)
本轮的最后一贴,真题中涉及计网的部分彻底总结完!后期的3轮总结可能会上一些大题,比如路由转发、子网划分什么的,以及重点的背诵内容~ 上期目录: CN考研真题知识点二轮归纳(4)https://jslhyh32…...

windows系统 生成RSA密钥对
在Windows系统上生成密钥对,可以使用多种方法,这里将介绍两种常用的方法: 方法1: 使用PuTTYgen PuTTYgen是PuTTY套件的一部分,是在Windows上生成SSH密钥对的一个流行工具。如果你的目的是SSH密钥对,你可以这样操作&a…...

大文件分片上传并发
我这边使用的是boostrap-fileimput 初始化文件上传框 $(document).ready(function () {$("#file-upload_import").fileinput({uploadUrl: "#",language: "zh", //设置语言showPreview: true,autoReplace: true,// uploadUrl: "/uact/uploa…...
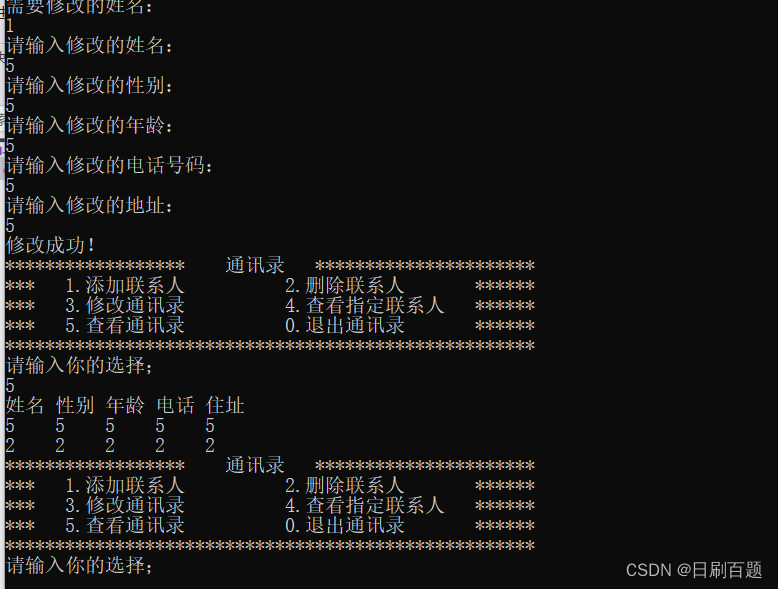
数据结构——基于顺序表实现通讯录
一、. 基于动态顺序表实现通讯录 1.1 功能要求 1)⾄少能够存储100个⼈的通讯信息 2)能够保存⽤⼾信息:名字、性别、年龄、电话、地址等 3)增加联系⼈信息 4)删除指定联系⼈ 5)查找制定联系⼈ 6&…...
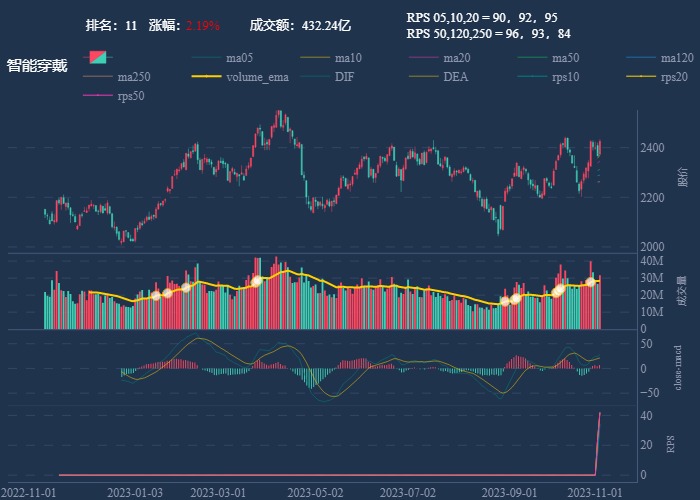
行业追踪,2023-11-03
自动复盘 2023-11-03 凡所有相,皆是虚妄。若见诸相非相,即见如来。 k 线图是最好的老师,每天持续发布板块的rps排名,追踪板块,板块来开仓,板块去清仓,丢弃自以为是的想法,板块去留让…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...
