VUE DIFF算法之快速DIFF
VUE DIFF算法系列讲解
VUE 简单DIFF算法
VUE 双端DIFF算法
文章目录
- VUE DIFF算法系列讲解
- 前言
- 一、快速DIFF的代码实现
- 二、实践
- 练习1
- 练习2
- 总结
前言
本节我们来写一下VUE3中新的DIFF算法-快速DIFF,顾名思义,也就是目前最快的DIFF算法(在VUE中)
本节内容值包括快速DIFF算法的实现,不考虑最长递增子序列算法的实现
一、快速DIFF的代码实现
相对于我们此系列的前两种DIFF算法,此DIFF算法在进入真正的DIFF算法之前,会有一个预处理的过程,这个主要是借鉴了纯文本Diff算法的思想。下边,我们就直接通过代码看下整个Diff的实现流程。
const oldChildren = n1.children;
const newChildren = n2.children;// 预处理开始
// 处理新旧子节点的头部可复用节点
let j = 0;
let oldVNode = oldChildren[j];
let newVNode = newChildren[j];
while (oldVNode.key === newVNode.key) {// 打补丁patch(oldVNode, newVNode, container);// 更新VNodej++;oldVNode = oldChildren[j];newVNode = newChildren[j];
}// 处理新旧节点尾部可复用节点, 因为新旧子节点长度可能不一致,所以需要定义两个变量
let oldEnd = oldChildren.length - 1;
let newEnd = newChildren.length - 1;oldVNode = oldChildren[oldEnd];
newVNode = newChildren[newEnd];while (oldVNode.key === newVNode.key) {// 打补丁patch(oldVNode, newVNode, container);// 更新VNodeoldEnd--;newEnd--;oldVNode = oldChildren[oldEnd];newVNode = newChildren[newEnd];
}
// 预处理结束后// 预处理结束会有三种情况:1.新子节点有剩余;2.旧街店有剩余;3:新旧节点均有剩余
if (j > oldEnd && j <= newEnd) {// 如果新子节点有剩余// 获取锚点idlet anchorIdx = newEnd + 1;// 获取锚点node,如果let anchor = anchorIdx === newChildren.length ? newChildren[anchorIdx].el : null;while (j <= newEnd) {// 挂载patch(null, newChildren[j++], container, anchor);}
} else if (j > newEnd && j <= oldEnd) {// 如果旧节点有剩余,则需要卸载while (j <= oldEnd) {unmount(oldChildren[j++]);}
} else {// 如果新旧节点均有剩余// 构造source数组const count = newEnd - j + 1;let source = new Array(count);source.fill(-1);// 新旧子节点的起始indexconst oldStart = j;const newStart = j;let pos = 0;let moved = false;// 构建新子节点的{key: index} 对象const keyIndex = {};for (let i = newStart; i < newEnd; i++) {keyIndex[newChildren[i].key] = i;}// 保存已被处理过的旧子节点数let patched = 0;// 填充sourcefor (let i = oldStart; i <= oldEnd; i++) {oldVNode = oldChildren[i];if (patched <= count) {const k = keyIndex[oldVNode.key];if (k !== undefined) {// 打补丁newVNode = newChildren[i];patch(oldVNode, newVNode, container);patched++;source[k - newStart] = i;if (k < pos) {moved = true;} else {pos = k;}} else {// 没有找到,卸载unmount(oldChildren[i]);}} else {// 处理数已等于新子节点数,其余卸载unmount(oldChildren[i]);}}// 如果需要移动if (moved) {const seq = lis(source);let s = seq.length - 1;let i = count - 1;for (i; i >= 0; i--)if (source[i] === -1) {// 这种情况属于新增const pos = i + newStart;const newVNode = newChildren[pos];// 获取锚点的索引const newPos = pos + 1;// 锚点const anchor = newPos < newChildren.length ? newChildren[newPos] : null;// 挂载patch(null, newVNode, container, anchor);} else if (seq[s] !== i) {// 这种情况需要移动const pos = i + newStart;const newVNode = newChildren[pos];// 获取锚点的索引const newPos = pos + 1;// 锚点const anchor = newPos < newChildren.length ? newChildren[newPos] : null;// 挂载insert(newVNode, container, anchor);} else {// 当 i === seq[j] 时,说明该位置的节点不需要移动// 并让 s 指向下一个位置s--;}}
}
二、实践
练习1
// 旧子节点
p-1 p-2 p-3
// 新子节点
p-1 p-3// 预处理开始
// while循环对比,预处理头部可服用量节点
let j = 0
newVNode = p-1
oldVNode = p-1
// 第一次循环 j=0
newVNode.key === oldVNode.key 可复用 j++
newVNode = p-2
oldVNode = p-3
// 第二次循环
newVNode.key !== oldVNode.key 跳出循环// while循环对比,预处理尾部可服用量节点
let oldEnd = 2(oldChildren.length - 1);
let newEnd = 1(newChildren.length - 1);
oldVNode = p-3(oldChildren[oldEnd]);
newVNode = p-3(newChildren[newEnd]);
// 第一次循环 oldEnd=2 newEnd=1
newVNode.key === oldVNode.key 可复用 oldEnd-- newEnd--
newVNode = p-2
oldVNode = p-1
// 第二次循环 oldEnd=1 newEnd=0
newVNode.key !== oldVNode.key 跳出循环
// 预处理结束// 预处理结束,此时j(1)>newEnd(0) && j(1)<=oldEnd(1),说明旧的子节点有剩余,仅需要将剩余子节点卸载即可
练习2
// 旧子节点
p-1 p-2 p-3 p-4 p-6 p-5
// 新子节点
p-1 p-3 p-4 p-2 p-7 p-5// 预处理开始
// while循环对比,预处理头部可服用量节点
let j = 0
newVNode = p-1
oldVNode = p-1
// 第一次循环 j=0
newVNode.key === oldVNode.key 可复用 j++
newVNode = p-2
oldVNode = p-3
// 第二次循环
newVNode.key !== oldVNode.key 跳出循环// while循环对比,预处理尾部可服用量节点
let oldEnd = 5(oldChildren.length - 1);
let newEnd = 5(newChildren.length - 1);
oldVNode = p-5(oldChildren[oldEnd]);
newVNode = p-5(newChildren[newEnd]);
// 第一次循环 oldEnd=2 newEnd=1
newVNode.key(p-5) === oldVNode.key(p-5) 可复用 oldEnd-- newEnd--
newVNode = p-7
oldVNode = p-6
// 第二次循环 oldEnd=4 newEnd=4
newVNode.key !== oldVNode.key 跳出循环
// 预处理结束// 此时真实dom节点如下
p-1(✅) p-2 p-3 p-4 p-6 p-5(✅)
// 待处理
p-2 p-3 p-4 p-6---------------------------------------------
// 预处理结束,此时j(1)<=newEnd(4) && j(1)<=oldEnd(4),说明新旧的子节点有剩余,此时我们需要构建一个sourece数组,这个数组长度为新子节点在预处理后剩余未处理的节点数,并且初始值为-1// 新子节点未处理完的节点数
const count = newEnd - j + 1;
// 构建source数组
let source = new Array(count);
source.fill(-1);
// 定义新旧子节点的起始index
const oldStart = j(1);
const newStart = j(1);
// 定义在旧子节点便利过程中遇到的最大的索引值
let pos = 0;
// 代表是否需要移动节点
let moved = false;
// 定义一个数量表示,表示已经处理过的子节点数.如果已处理过的子节点数超过新子节点数,则表示其余的为多余节点,直接卸载
let patched = 0// 构建一个索引表,此表内存储新子节点中,key与index的映射
keyIndex = {p-3 : 1,p-4 : 2,p-2 : 3,p-7 : 4
}// 填充source数组并处理多余oldVNode
// 开始循环
// 第一次循环 i(oldStart) = 1; oldEnd = 4; count = 4; pos = 0;
oldVNode patched kp-2 0 3
k !== undefined patched++ pos=k i++
source = [-1, -1, 1, -1]
// 第二次循环 i = 2; oldEnd = 4; count = 4; pos = 3
oldVNode patched kp-3 1 1
k !== undefined patched++ moved = true
source = [2, -1, 1, -1]
// 第三次循环 i = 3; oldEnd = 4; count = 4; 因moved为true,所以不再需要关心pos
oldVNode patched kp-4 2 2
k !== undefined patched++
source = [2, 3, 1, -1]
// 第四次循环 i = 4; oldEnd = 4; count = 4;
oldVNode patched kp-6 3 undefined
k === undefined 卸载
source = [2, 3, 1, -1]
// 第四次循环 i = 5; oldEnd = 4; i > oldEnd 跳出循环// 此时真实dom节点如下
p-1(✅) p-2 p-3 p-4 p-6(❌) p-5(✅)
// 待处理
p-2 p-3 p-4
---------------------------------------------------------// 因moved为true,所以需要进行移动
// 构建一个最长递增子序列(此节中暂不考虑最长递增子序列算法)
const seq = [0, 1]
// 定义s, 其值为最长递增子序列的最大index
let s = 1
// 定义i, 其值为source的最大index
let i = 3// 开始循环
// 第一次循环 i = 3;
source[3] = -1, 则此节点为新增节点,需要挂载,锚点为p-5
// 此时真实dom节点如下
p-1(✅) p-2 p-3 p-4 p-7(✅) p-5(✅)// 第二次循环 i = 2;
source[2] = 1,
seq[1] !== 2 此节点需要移动, 锚点为p-7
// 此时真实dom节点如下
p-1(✅) p-3 p-4 p-2(✅) p-7(✅) p-5(✅)// 第三次循环 i = 1;
source[1] = 3,
seq[1] === 1 此节点不需要移动 s--
// 此时真实dom节点如下
p-1(✅) p-3 p-4(✅) p-2(✅) p-7(✅) p-5(✅)// 第四次循环 i = 0;
source[0] = 2,
seq[0] === 0 此节点不需要移动
// 此时真实dom节点如下
p-1(✅) p-3(✅) p-4(✅) p-2(✅) p-7(✅) p-5(✅)
总结
快速Diff算法的整体逻辑还是比较容易理解的,其中比较巧妙的是预处理和source的用法。学习快速Diff算法不仅让我们更深刻的了解了VUE3,同时其中的一些核心逻辑,也可以为我们的日常开发工作中提供一些开发思路。
参考:<<vue设计与实现>>第10章
github:link
相关文章:

VUE DIFF算法之快速DIFF
VUE DIFF算法系列讲解 VUE 简单DIFF算法 VUE 双端DIFF算法 文章目录VUE DIFF算法系列讲解前言一、快速DIFF的代码实现二、实践练习1练习2总结前言 本节我们来写一下VUE3中新的DIFF算法-快速DIFF,顾名思义,也就是目前最快的DIFF算法(在VUE中&…...

一文掌握如何轻松稿定项目风险管理【静说】
风险管理对于每个项目经理和PMO都非常重要,如果管理不当会出现很多问题,咱们以前分享过很多风险管理的内容: 风险无处不在,一旦发生,会对一个或多个项目目标产生积极或消极影响的确定事件或条件。那么接下来介绍下五大…...
操作系统权限提升(十四)之绕过UAC提权-基于白名单AutoElevate绕过UAC提权
系列文章 操作系统权限提升(十二)之绕过UAC提权-Windows UAC概述 操作系统权限提升(十三)之绕过UAC提权-MSF和CS绕过UAC提权 注:阅读本编文章前,请先阅读系列文章,以免造成看不懂的情况!! 基于白名单AutoElevate绕过…...
ecology9-谷歌浏览器下-pdf.js在渲染时部分发票丢失文字 问题定位及解决
问题 问题描述 : 在谷歌浏览器下,pdf.js在渲染时部分发票丢失文字;360浏览器兼容模式不存在此问题 排查思路:1、对比谷歌浏览器的css样式和360浏览器兼容模式下的样式,没有发现关键差别 2、✔使用Fiddler修改网页js D…...

JavaScript Window Navigator
文章目录JavaScript Window NavigatorWindow Navigator警告!!!浏览器检测JavaScript Window Navigator window.navigator 对象包含有关访问者浏览器的信息。 Window Navigator window.navigator 对象在编写时可不使用 window 这个前缀。 实例 <div id"example"…...

Linux基础命令-du查看文件的大小
文章目录 du 命令介绍 语法格式 基本参数 参考实例 1)以人类可读形式显示指定的文件大小 2)显示当前目录下所有文件大小 3)只显示目录的大小 4)显示根下哪个目录文件最大 5)显示所有文件的大小 6࿰…...
文献计量分析方法:Citespace安装教程
Citespace是一款由陈超美教授开发的可用于海量文献可视化分析的软件,可对Web of Science,Scopus,Pubmed,CNKI等数据库的海量文献进行主题、关键词,作者单位、合作网络,期刊、发表时间,文献被引等…...

MVI 架构更佳实践:支持 LiveData 属性监听
前言MVI架构为了解决MVVM在逻辑复杂时需要写多个LiveData(可变不可变)的问题,使用ViewState对State集中管理,只需要订阅一个 ViewState 便可获取页面的所有状态通过集中管理ViewState,只需对外暴露一个LiveData,解决了MVVM模式下LiveData膨胀…...

LeetCode438 找到字符串中所有字母异位词 带输入和输出
题目: 给定两个字符串 s 和 p,找到 s 中所有 p 的 异位词 的子串,返回这些子串的起始索引。不考虑答案输出的顺序。 异位词 指由相同字母重排列形成的字符串(包括相同的字符串)。 示例 1: 输入: s “cbaebabacd”, …...

ACSC 2023 比赛复现
Admin Dashboard 在 index.php 中可以看到需要访问者是 admin 权限,才可以看到 flag。 report.php 中可以让 admin bot 访问我们输入的 url,那么也就是说可以访问 addadmin.php 添加用户。 在 addadmin.php 中可以添加 admin 用户,但是需…...

【Linux驱动开发100问】什么是模块?如何编写和使用模块?
🥇今日学习目标:什么是Linux内核? 🤵♂️ 创作者:JamesBin ⏰预计时间:10分钟 🎉个人主页:嵌入式悦翔园个人主页 🍁专栏介绍:Linux驱动开发100问 什么是模块…...

Android 9.0 Recent列表不显示某个app
1.概述 在9.0的系统产品rom定制化开发中,在一些产品定制化需求中,也是有很多重要的功能实现的,比如在某些app的开发中 由于不想被杀掉,所以就不想出现在recent的列表中,因此就需要从recent的列表中,去掉这个app的显示,然后这里有 两种方法实现这个功能,一种是在app中就…...
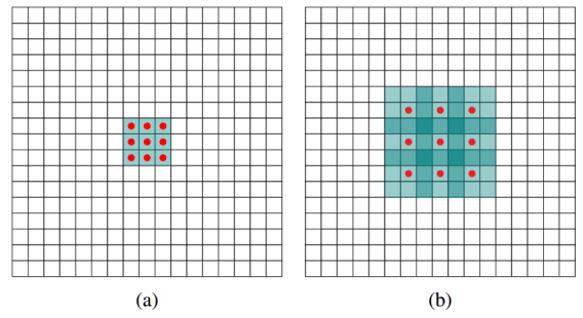
深度学习之卷积神经网络学习笔记一
1. 引言深度学习是一系列算法的统称,包括卷积神经网络(CNN),循环神经网络(RNN),自编码器(AE),深度置信网络(DBN),生成对抗…...
黑盒测试的常用方法
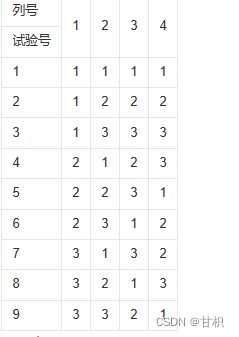
这里我们先设置一个示例,后面的文章中会根据示例来进行讲解 假设有一个程序是判断一个整形数字是否属于1-100 目录 1.等价类法 2.边界值法 3.判定表法 4.场景设计法 5.错误猜测法 6.正交法 1.等价类法 概念:系统性的确定要输入的测试条件的方法可以看出概念非常抽象,那…...
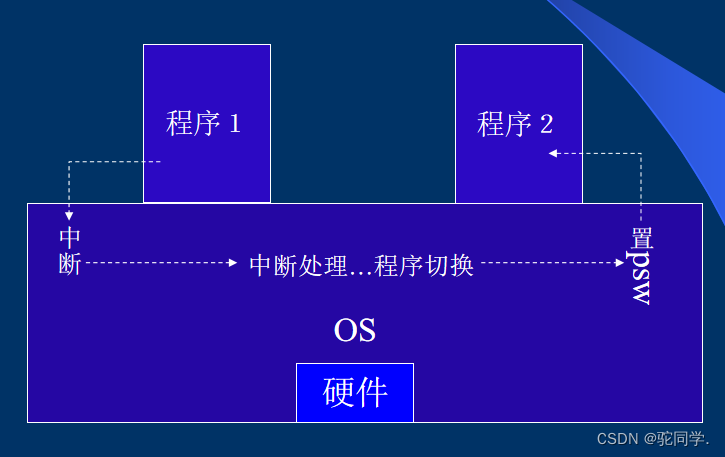
操作系统笔记-第一章
文章目录操作系统概述1. 操作系统的概念1.1 操作系统的地位1.2 操作系统的作用1.3 操作系统的定义2. 操作系统的历史2.1 操作系统的产生2.1.1 手动操作阶段(20世纪40年代)2.1.2 批处理阶段(20世纪50年代)2.1.3 执行系统阶段&#…...

daillist
daillist #重要说明: #[1]任意两个配置参数之间必须以空格隔开,否则,拨号脚本无法识别。 #[2]Info格式说明:厂商名简称_制式_频段 #VID #PID #PORT_M #PORT_A #PORT_G #script_*99# #script_#777 #Info 05c6 9025 /dev/ttyUSB1 /dev/ttyUSB2 …...
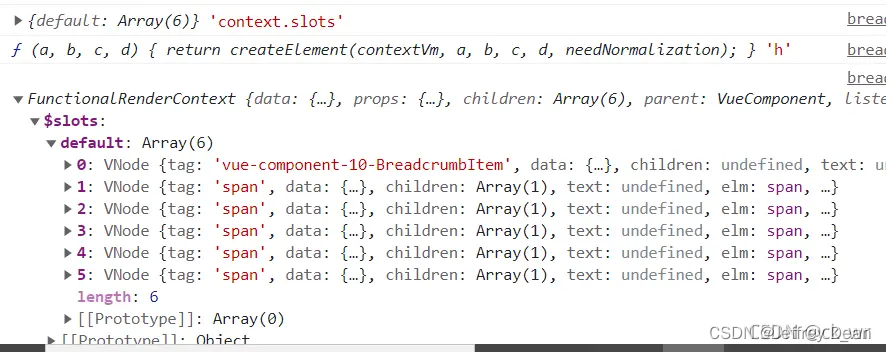
vue中render函数的作用和参数(vue2中render函数用法)
render 函数是 Vue2.x 新增的一个函数、主要用来提升节点的性能,它是基于 JavaScript 计算。使用 Render 函数将 Template 里面的节点解析成虚拟的 Dom 。Vue 推荐在绝大多数情况下使用模板来创建 HTML。然而在一些场景中,需要 JavaScript 的完全编程能力…...
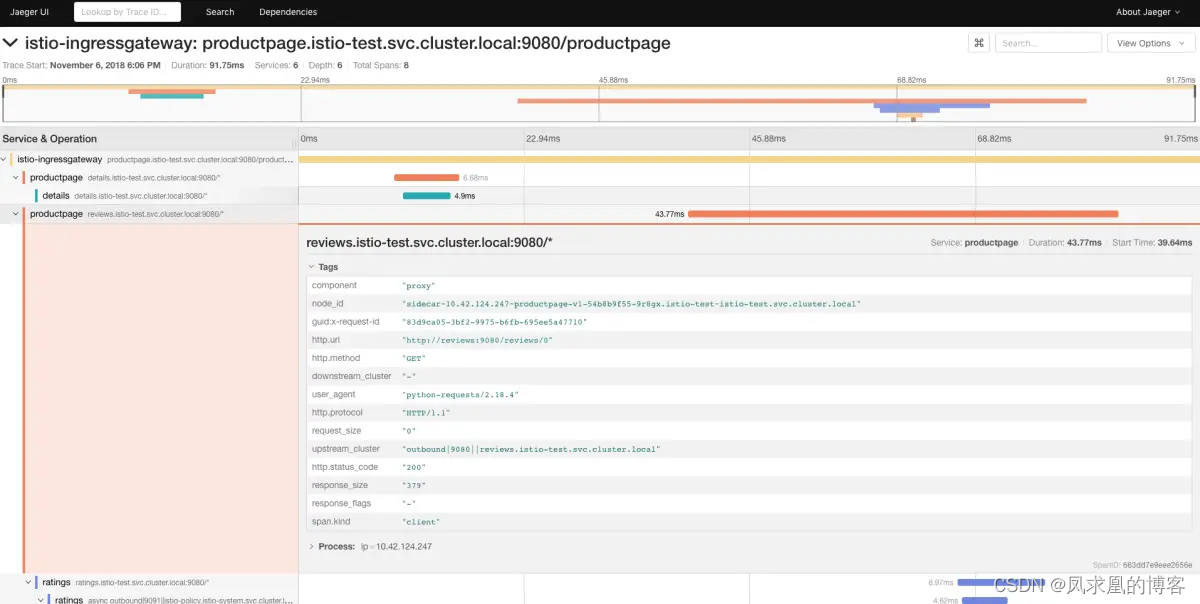
基于Istio的高级流量管理二(Envoy流量劫持、Istio架构、高级流量管理)
文章目录一、Envoy流量劫持机制(Iptables规则流转)1、流量出向劫持流程(1)envoy怎样劫持入向流量?(2)Envoy劫持到流量之后,干什么?(查询目的地)&a…...

Sharding-Springboot-mybatis-plus整合(三)-inline策略
Sharding-Springboot-mybatis-plus整合(三) 1.简介 本节目标,使用SpringBoot整合Sharding和Mybatis-Plus验证上节分片策略 从配置文件上看策略包括( inline、standard、complex、hint) 环境搭建以inline策略演示 …...
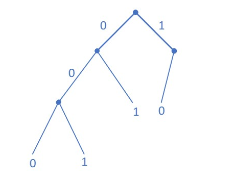
编码的基本概念
本专栏包含信息论与编码的核心知识,按知识点组织,可作为教学或学习的参考。markdown版本已归档至【Github仓库:information-theory】,需要的朋友们自取。或者公众号【AIShareLab】回复 信息论 也可获取。 文章目录信源编码分类前缀…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...
