Android 9.0 Recent列表不显示某个app
1.概述
在9.0的系统产品rom定制化开发中,在一些产品定制化需求中,也是有很多重要的功能实现的,比如在某些app的开发中
由于不想被杀掉,所以就不想出现在recent的列表中,因此就需要从recent的列表中,去掉这个app的显示,然后这里有
两种方法实现这个功能,一种是在app中就可以实现,还有一种就是在frameworks层中实现这个功能也是可以的,
1.1, app中处理
第一中改法就是为该应用AndroidManifest xml文件中主MainActivity设置属性
android:excludeFromRecents=“true”
例如:
<activity android:name=".MainActivity"
android:excludeFromRecents="true"
android:label="@string/app_name">
<intent-filter>
<action android:name="android.intent.action.MAIN" />
<category android:name="android.intent.category.LAUNCHER" />
</intent-filter><
相关文章:

Android 9.0 Recent列表不显示某个app
1.概述 在9.0的系统产品rom定制化开发中,在一些产品定制化需求中,也是有很多重要的功能实现的,比如在某些app的开发中 由于不想被杀掉,所以就不想出现在recent的列表中,因此就需要从recent的列表中,去掉这个app的显示,然后这里有 两种方法实现这个功能,一种是在app中就…...
深度学习之卷积神经网络学习笔记一
1. 引言深度学习是一系列算法的统称,包括卷积神经网络(CNN),循环神经网络(RNN),自编码器(AE),深度置信网络(DBN),生成对抗…...
黑盒测试的常用方法
这里我们先设置一个示例,后面的文章中会根据示例来进行讲解 假设有一个程序是判断一个整形数字是否属于1-100 目录 1.等价类法 2.边界值法 3.判定表法 4.场景设计法 5.错误猜测法 6.正交法 1.等价类法 概念:系统性的确定要输入的测试条件的方法可以看出概念非常抽象,那…...
操作系统笔记-第一章
文章目录操作系统概述1. 操作系统的概念1.1 操作系统的地位1.2 操作系统的作用1.3 操作系统的定义2. 操作系统的历史2.1 操作系统的产生2.1.1 手动操作阶段(20世纪40年代)2.1.2 批处理阶段(20世纪50年代)2.1.3 执行系统阶段&#…...

daillist
daillist #重要说明: #[1]任意两个配置参数之间必须以空格隔开,否则,拨号脚本无法识别。 #[2]Info格式说明:厂商名简称_制式_频段 #VID #PID #PORT_M #PORT_A #PORT_G #script_*99# #script_#777 #Info 05c6 9025 /dev/ttyUSB1 /dev/ttyUSB2 …...
vue中render函数的作用和参数(vue2中render函数用法)
render 函数是 Vue2.x 新增的一个函数、主要用来提升节点的性能,它是基于 JavaScript 计算。使用 Render 函数将 Template 里面的节点解析成虚拟的 Dom 。Vue 推荐在绝大多数情况下使用模板来创建 HTML。然而在一些场景中,需要 JavaScript 的完全编程能力…...
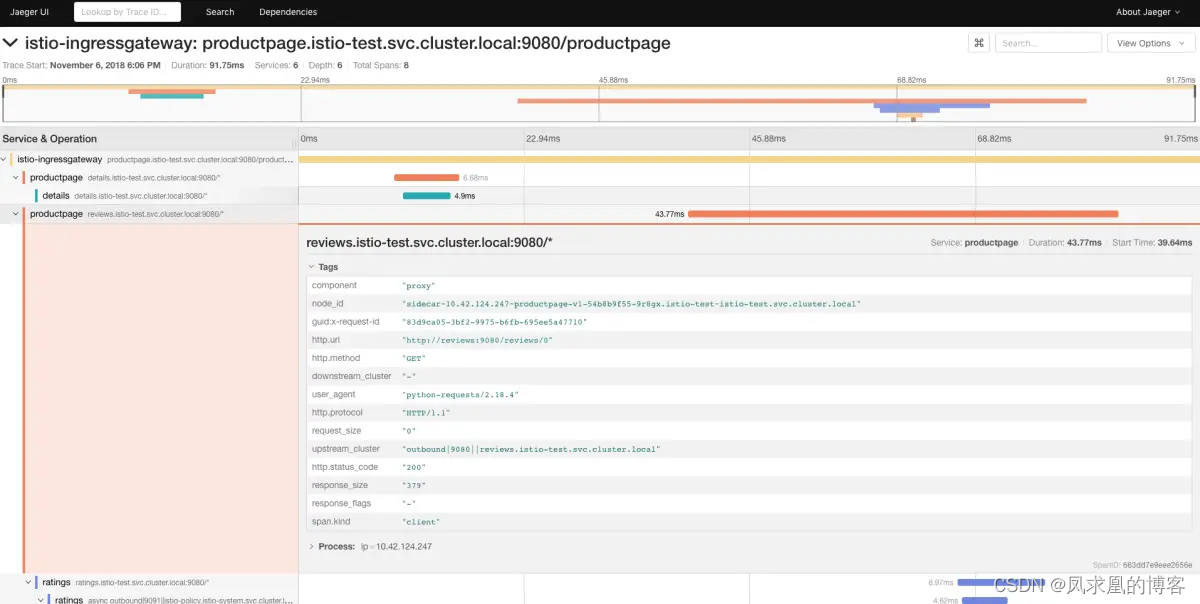
基于Istio的高级流量管理二(Envoy流量劫持、Istio架构、高级流量管理)
文章目录一、Envoy流量劫持机制(Iptables规则流转)1、流量出向劫持流程(1)envoy怎样劫持入向流量?(2)Envoy劫持到流量之后,干什么?(查询目的地)&a…...

Sharding-Springboot-mybatis-plus整合(三)-inline策略
Sharding-Springboot-mybatis-plus整合(三) 1.简介 本节目标,使用SpringBoot整合Sharding和Mybatis-Plus验证上节分片策略 从配置文件上看策略包括( inline、standard、complex、hint) 环境搭建以inline策略演示 …...
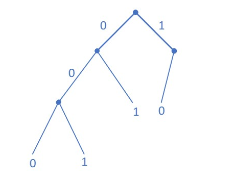
编码的基本概念
本专栏包含信息论与编码的核心知识,按知识点组织,可作为教学或学习的参考。markdown版本已归档至【Github仓库:information-theory】,需要的朋友们自取。或者公众号【AIShareLab】回复 信息论 也可获取。 文章目录信源编码分类前缀…...

函数指针与指针函数的区别
目录:一、函数指针1 函数类型2 函数指针(指向函数的指针)3 函数指针数组二.函数指针和指针函数比较1 定义不同2 写法不同3.用法不同三.函数指针做函数参数(回调函数)1 利用回调函数实现打印任意类型数据2 提供能够打印任意类型数组函数3 利用回调函数 提供查找功能四…...

死锁的四个必要条件以及如何避免死锁
死锁的四个必要条件以及如何避免死锁 一.什么是死锁?二.死锁的四个必要条件 1.互斥条件:2.请求与保持条件:3.不剥夺条件:4.循环等待条件: 三.如何避免死锁 1.破坏请求保持条件2.破坏不剥夺条件3.破坏循环等待条件 死锁的四个必要条件以及如…...
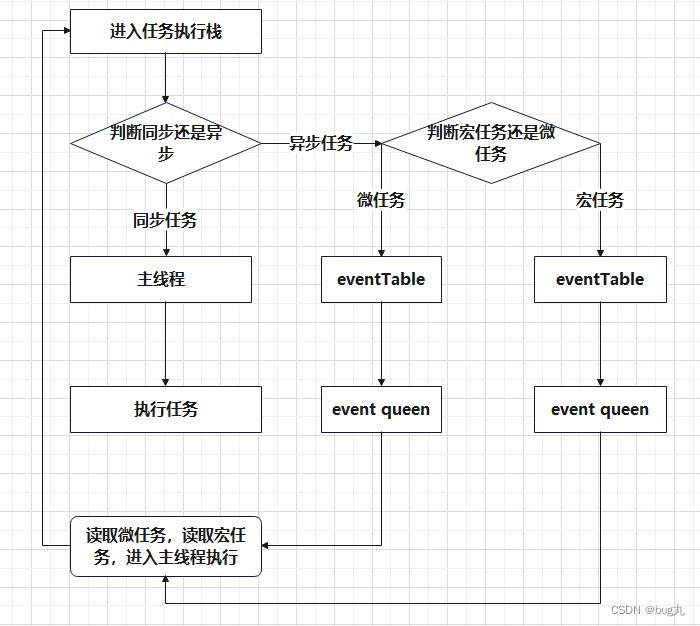
浏览器多线程到事件循环机制
浏览器与js运行机制 进程与线程 进程 进程是CPU分配资源的最小单位,它是一个可以自己独立运行且拥有自己资源空间的任务程序;包括程序以及程序所使用的内存及系统资源 线程 线程是CPU调度的最小单位,它就是程序中的一个执行流࿱…...
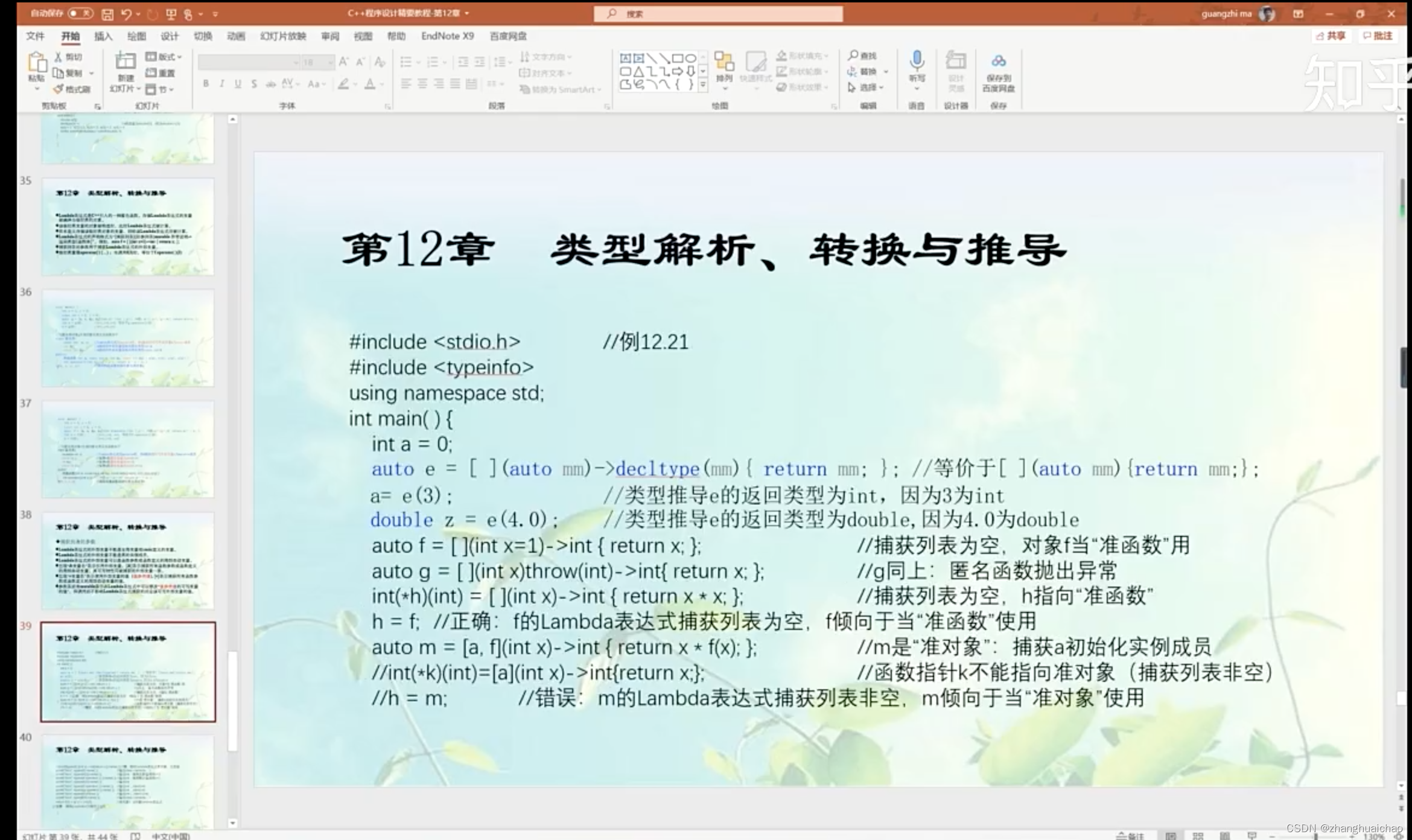
Lambda表达式的本质
一直想写一篇文章,来总结lambda表达式,但是之前感觉总结的不是特别到位,现在看了几篇文章和视频后,感觉对lambda表达式有了比较深刻的认识,现在进行记录总结如下: lambda表达式又叫做匿名函数,…...

类的加载过程(生命周期)
类的加载过程(生命周期) 一、装载:通过一个类的全限定名获取定义此类的二进制字节流将这个字节流所代表的静态存储结构转化为方法区的运行时数据结构在内存中生成一个代表这个类的java.lang.Class对象(将字节码加载到内存中),作为…...

2023最新谷粒商城笔记之MQ消息队列篇(全文总共13万字,超详细)
MQ消息队列 其实队列JDK中本身就有,不过这种队列也只能单体服务可能会使用,一旦项目使用的分布式架构,那么一定还是需要用到一个消息中间件的。我们引入消息队列的原因就是对我们的页面相应速度再优化,让用户的体验更好ÿ…...
多变量线性回归模型
多变量线性回归模型 模型参数为n1维向量,此时模型公式为 hθ(x)θ0x0θ1x1θ2x2...θnxnh_{\theta}(x)\theta_{0}x_{0}\theta_{1}x_{1}\theta_{2}x_{2}...\theta_{n}x_{n} hθ(x)θ0x0θ1x1θ2x2...θnxn 可以简化为 hθ(x)θTXh_{\theta}(x)\th…...
php 基于ICMP协议实现一个ping命令
php 基于ICMP协议实现一个ping命令 网络协议是什么ICMP 协议什么是ICMP?ICMP 的主要功能ICMP 在 IPv4 和 IPv6 的封装Wireshark抓包ICMP 请求包分析PHP构建 ICMP 数据包php中的 pack & unpack 函数字节和字符packunpackICMP计算校验和步骤总结网络协议是什么 网络协议&…...

Java基本数据类型
1.概述 佛说,大千世界,无奇不有。在这个世界里,物种的多样性,遍地开花,同样,在Java的世界里,也有着异曲同工之妙,Java秉承面向对象的特性,必然少不了区分对象的类型&…...

English Learning - L2 语音作业打卡 Day2 2023.2.22 周三
English Learning - L2 语音作业打卡 Day2 2023.2.22 周三💌 发音小贴士:💌 当日目标音发音规则/技巧:🍭 Part 1【热身练习】🍭 Part2【练习内容】🍭【练习感受】🍓元音[ ɑː ]&…...

45. 跳跃游戏 II
题目: 45. 跳跃游戏 II难度中等1974收藏分享切换为英文接收动态反馈给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 num…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强:基于微服务与容器化的解决方案
在大数据时代,海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构,在处理大规模数据抓取任务时展现出强大的能力。然而,随着业务规模的不断扩大和数据抓取需求的日益复杂,传统…...

DeepSeek源码深度解析 × 华为仓颉语言编程精粹——从MoE架构到全场景开发生态
前言 在人工智能技术飞速发展的今天,深度学习与大模型技术已成为推动行业变革的核心驱动力,而高效、灵活的开发工具与编程语言则为技术创新提供了重要支撑。本书以两大前沿技术领域为核心,系统性地呈现了两部深度技术著作的精华:…...
)
41道Django高频题整理(附答案背诵版)
解释一下 Django 和 Tornado 的关系? Django和Tornado都是Python的web框架,但它们的设计哲学和应用场景有所不同。 Django是一个高级的Python Web框架,鼓励快速开发和干净、实用的设计。它遵循MVC设计,并强调代码复用。Django有…...
