多变量线性回归模型
多变量线性回归模型
模型参数为n+1维向量,此时模型公式为
hθ(x)=θ0x0+θ1x1+θ2x2+...+θnxnh_{\theta}(x)=\theta_{0}x_{0}+\theta_{1}x_{1}+\theta_{2}x_{2}+...+\theta_{n}x_{n} hθ(x)=θ0x0+θ1x1+θ2x2+...+θnxn
可以简化为
hθ(x)=θTXh_{\theta}(x)=\theta^\mathrm{T}\mathrm{X} hθ(x)=θTX
此时的代价函数仍是所有建模误差的平方和,即
J(θ0,θ1,...,θn)=12m∑i=1m(hθ(x(i))−y(i))2J(\theta_{0},\theta_{1},...,\theta_{n})=\frac{1}{2m}\sum_{i=1}^{m}{(h_{\theta}(x^{(i)})-y^{(i)})^2} J(θ0,θ1,...,θn)=2m1i=1∑m(hθ(x(i))−y(i))2
此时的批量梯度算法为
θj:=θj−α∂∂θjJ(θ0,θ1,...,θn)\theta_{j}:=\theta_{j}-\alpha\frac{\partial }{\partial \theta_{j}}J(\theta_{0},\theta_{1},...,\theta_{n}) θj:=θj−α∂θj∂J(θ0,θ1,...,θn)
θj:=θj−α1m∑i=1m(hθ(x(i))−y(i))⋅xj(i)forj=0,1,...n\theta_{j}:=\theta_{j}-\alpha\frac{1}{m}\sum_{i=1}^{m}{(h_{\theta}(x^{(i)})-y^{(i)})\cdot x_{j}^{(i)}}\quad for\quad j=0,1,...n θj:=θj−αm1i=1∑m(hθ(x(i))−y(i))⋅xj(i)forj=0,1,...n
特征缩放
在多维特征问题中,特征尺度越相近,梯度下降算法收敛越快。 尽量将特征尺度xnx_nxn缩放到-1~1之间。μn\mu_nμn是平均值,sns_nsn是方差。
xn=xn−μnsnx_n=\frac{x_n-\mu_n}{s_n} xn=snxn−μn
学习率
我们不能提前预知梯度下降算法收敛所需的迭代次数,但可以通过绘制迭代次数和代价函数的图表来观测算法在何时趋于收敛。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-4mSi7pO3-1677383749764)(C:\Users\20491\AppData\Roaming\Typora\typora-user-images\image-20230222205742828.png)]](https://img-blog.csdnimg.cn/549215d3048f44bbae411f0e908863f3.png)
常用的学习率为0.01,0.03,0.1,0.3,1,3,10
多项式回归
线性回归不适用所有的模型,有时候可能需要二次方、三次方等模型,比如
hθ(x)=θ0+θ1x1+θ2x22+θ3x33h_{\theta}(x)=\theta_0+\theta_1x_1+\theta_2x^2_2+\theta_3x^3_3 hθ(x)=θ0+θ1x1+θ2x22+θ3x33
hθ(x)=θ0+θ1x1+θ2x2h_{\theta}(x)=\theta_0+\theta_1x_1+\theta_2\sqrt x_2 hθ(x)=θ0+θ1x1+θ2x2
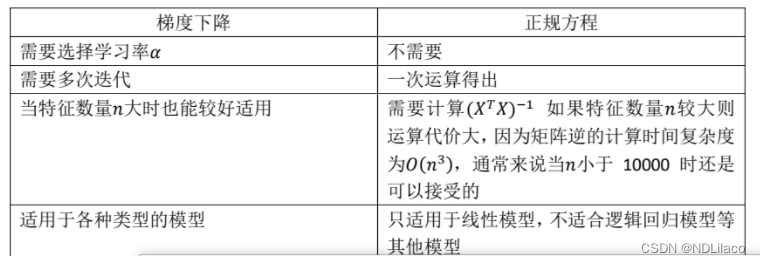
正规方程
通过正规方程解出向量,其中XXX为特征矩阵
θ=(XTX)−1XTy\theta=(X^{\mathrm T}X)^{-1}X^{\mathrm T}y θ=(XTX)−1XTy
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-4pzQdqn3-1677383749764)(C:\Users\20491\AppData\Roaming\Typora\typora-user-images\image-20230223112740746.png)]](https://img-blog.csdnimg.cn/3dc2c5e2543344d8b1da5f576b12d391.png)
相关文章:
多变量线性回归模型
多变量线性回归模型 模型参数为n1维向量,此时模型公式为 hθ(x)θ0x0θ1x1θ2x2...θnxnh_{\theta}(x)\theta_{0}x_{0}\theta_{1}x_{1}\theta_{2}x_{2}...\theta_{n}x_{n} hθ(x)θ0x0θ1x1θ2x2...θnxn 可以简化为 hθ(x)θTXh_{\theta}(x)\th…...
php 基于ICMP协议实现一个ping命令
php 基于ICMP协议实现一个ping命令 网络协议是什么ICMP 协议什么是ICMP?ICMP 的主要功能ICMP 在 IPv4 和 IPv6 的封装Wireshark抓包ICMP 请求包分析PHP构建 ICMP 数据包php中的 pack & unpack 函数字节和字符packunpackICMP计算校验和步骤总结网络协议是什么 网络协议&…...

Java基本数据类型
1.概述 佛说,大千世界,无奇不有。在这个世界里,物种的多样性,遍地开花,同样,在Java的世界里,也有着异曲同工之妙,Java秉承面向对象的特性,必然少不了区分对象的类型&…...

English Learning - L2 语音作业打卡 Day2 2023.2.22 周三
English Learning - L2 语音作业打卡 Day2 2023.2.22 周三💌 发音小贴士:💌 当日目标音发音规则/技巧:🍭 Part 1【热身练习】🍭 Part2【练习内容】🍭【练习感受】🍓元音[ ɑː ]&…...

45. 跳跃游戏 II
题目: 45. 跳跃游戏 II难度中等1974收藏分享切换为英文接收动态反馈给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 num…...
)
应届生Java面试50题线程篇(含解析)
什么是线程? 答:线程是操作系统能够进行运算调度的最小单位,是程序执行流的最小单元。在Java中,可以通过实现Runnable接口或继承Thread类来创建线程。 创建线程的方式有哪些?各自的优缺点是什么? 继承 Thread 类&…...
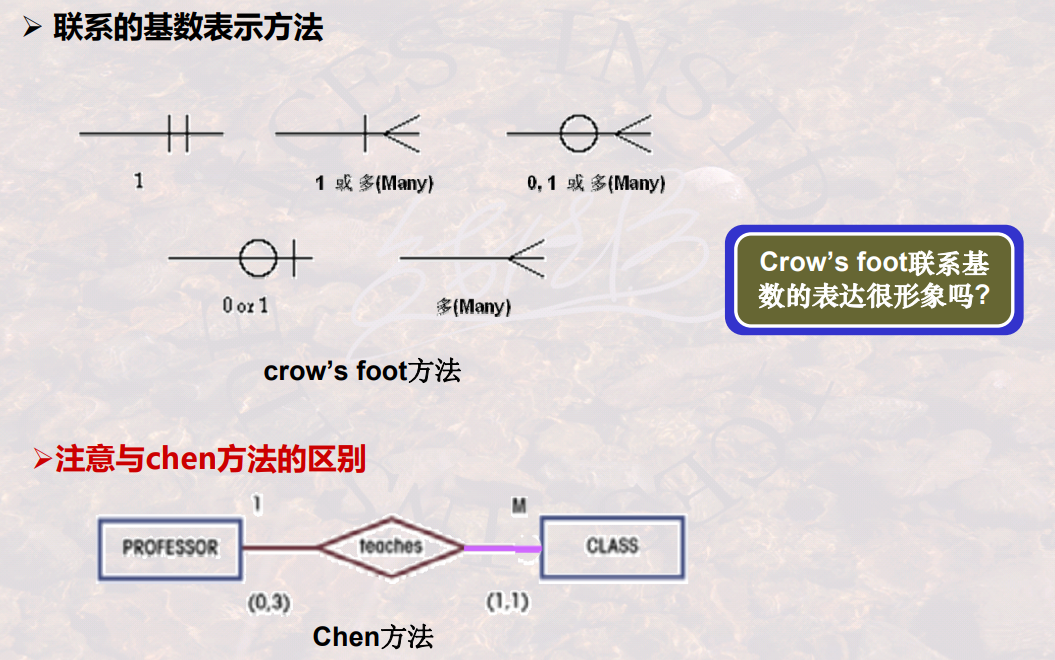
【数据库】第七章 数据库设计
第七章数据库设计 数据库设计概述 数据库设计的基本步骤 需求分析概念结构设计逻辑结构设计物理结构设计数据库实施数据库运行和维护 需求分析 收集需求,理解需求 收集各个角色的需求 概念数据库设计 建立概念模型 ,E-R图/IDEF1x图 消除冲突&…...

Burp Suite 常用模块简介
Burp Suite 常用模块分为 目标站点(target)模块 代理(proxy)模块 攻击(Intruder)模块 重放(Repeater) 模块 Target模块是对站点资源的收集,与站点各资源包发出和相应包的记录 Proxy模块是核心模块,可以拦截数据包发送往浏览器,进行修改后再…...

QML Item和Rectangle详解
1.Item和Rectangle Item类型是Qt Quick中所有可视项的基本类型。 Qt Quick中的所有可视项都继承Item。尽管Item对象没有视觉外观,但它定义了视觉项中常见的所有属性,例如x和y位置、宽度和高度、锚定和键处理支持。 Rectangle继承自Item,多…...
(六))
常见前端基础面试题(HTML,CSS,JS)(六)
GET 和 POST 的区别 从 http 协议的角度来说,GET 和 POST 它们都只是请求行中的第一个单词,除了语义不同,其实没有本质的区别。 之所以在实际开发中会产生各种区别,主要是因为浏览器的默认行为造成的。 受浏览器的影响…...

深度学习 李沐报错
3.6. softmax回归的从零开始实现 — 动手学深度学习 2.0.0 documentation softmax从0开始实现 函数执行需要加main指定 改成这样 if __name__"__main__":print(evaluate_accuracy(net, test_iter)) 不然会这样出错 RuntimeError: An attempt has been m…...

【JAVA程序设计】(C00104)基于Springboot的家庭理财管理系统——有文档
基于Springboot的家庭理财管理系统项目简介项目获取开发环境项目技术运行截图运行视频项目简介 基于Springboot开发的家庭理财管理系统设计与实现共分为三个角色:系统管理员、家庭管理员、家庭用户 管理员角色包含以下功能: 用户管理、修改密码、角色管…...
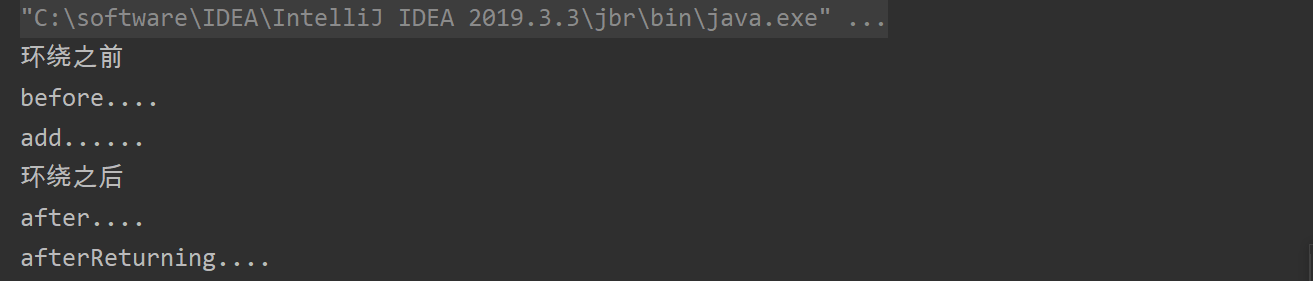
【第五章 AOP概述,底层原理,AOP术语,切入点表达式,AOP操作(基于注解方式,基于xml配置文件)】
第五章 AOP概述,底层原理,AOP术语,切入点表达式,AOP操作(基于注解方式,基于xml配置文件) 1.AOP概述: (1)什么是AOP: ①面向切面编程(…...
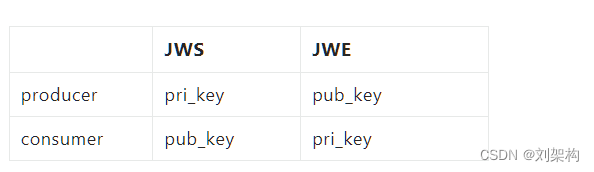
面试官: 你知道 JWT、JWE、JWS 、JWK嘛?
想起了 之前做过的 很多 登录授权 的项目 它相比原先的session、cookie来说,更快更安全,跨域也不再是问题,更关键的是更加优雅 ,所以今天总结了一篇文章来介绍他 JWT 指JSON Web Token,如果在项目中通过 jjwt 来支持 J…...
基于企业微信应用消息的每日早安推送
基于企业微信应用消息的每日早安推送 第一步:注册企业微信 企业微信注册地址:https://work.weixin.qq.com/wework_admin/register_wx 按照正常流程填写信息即可,个人也可以注册企业微信,不需要公司 注册完成后,登录…...
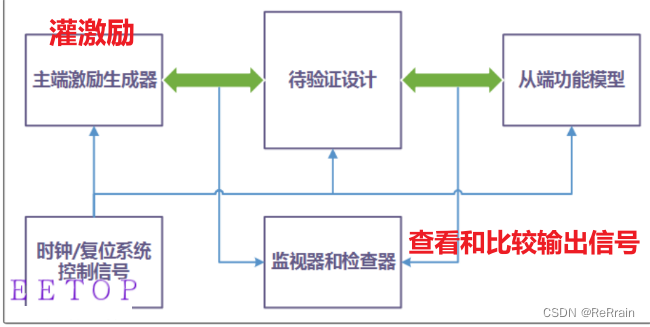
【数字IC基础】黑盒验证、白盒验证、 灰盒验证
文章目录 一、黑盒验证二、白盒验证三、灰盒验证一、黑盒验证 1、黑盒验证:大多数基于仿真的验证环境都是黑盒验证;2、不需要知道设计的内部结构和特性,只需要在输入端口打激励,观察输出即可;3、验证工程师学习设计的规格,然后编写验证环境中的 drivers, monitors, check…...

管理的本质是达成目标
“没有目标,其实就没有管理学存在的意义。要有效地使用管理学的智慧,首先要建立清晰的目标。” - 《宁向东的管理学课》 起源 最近开始刷很久之前就在得到上买了的已经起灰了的课程,看到这句话觉得很有道理。 思考 这里面有一个很重要的词…...
常用缩写)
【数字IC基础】IC(Integrated Circuit,集成电路)常用缩写
文章目录 1、集成电路:2、数字IC设计相关步骤:3、数字设计相关概念:4、验证相关:5、语言类:6、IC设计相关工具:7、存储器相关:8、总线协议类:9、文件格式类:10、标准和规范:11、其它:1、集成电路: 缩写全称中文翻译LSILarge-scale intergrated circuit大规模集成电…...
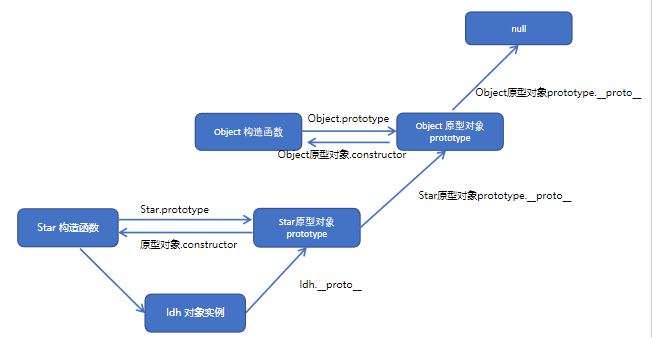
JavaScript 高级1 :面向对象
JavaScript 高级1 :面向对象 Date: January 16, 2023 Text: 面向对象、ES6中类和对象、类的继承、面向对象案例 目标: 能够说出什么是面向对象 能够说出类和对象的关系 能够使用 class 创建自定义类型 能够说出什么是继承 面向对象编程介绍 面向过…...
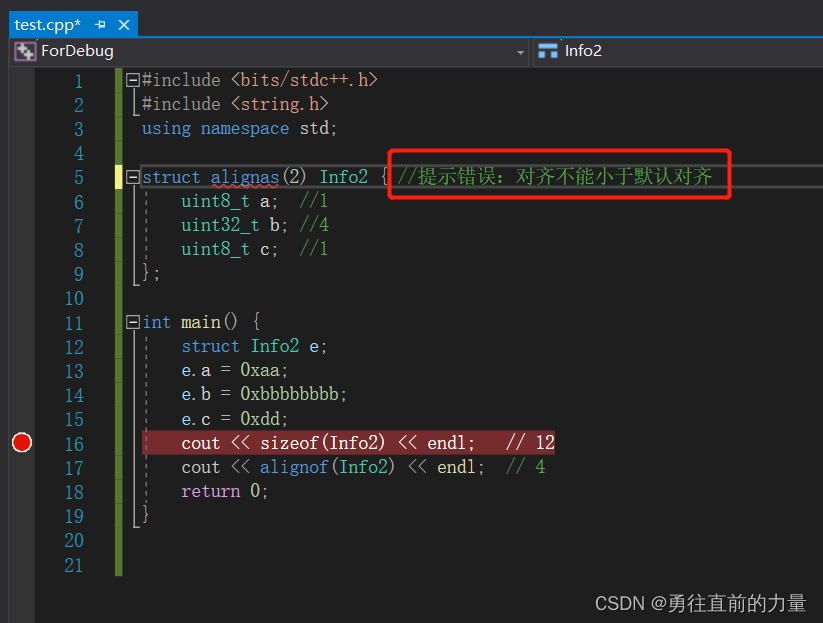
C语言结构体对齐
1. 结构体对齐 要点 变量只能存储在他的长度的整数倍地址上结构体整体对齐跟他的最长的字段整数倍对齐 栗子1 struct Example1 {char a; //1个字节int c; //4个字节short b; //2个字节 };std::cout << sizeof(Example1 ) << std::endl; // 12 std::cout &…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...
