深度学习 李沐报错
3.6. softmax回归的从零开始实现 — 动手学深度学习 2.0.0 documentation
softmax从0开始实现
函数执行需要加main指定
改成这样
if __name__=="__main__":print(evaluate_accuracy(net, test_iter))不然会这样出错
RuntimeError:
An attempt has been made to start a new process before the
current process has finished its bootstrapping phase.
This probably means that you are not using fork to start your
child processes and you have forgotten to use the proper idiom
in the main module:
if __name__ == '__main__':
freeze_support()
...
The "freeze_support()" line can be omitted if the program
is not going to be frozen to produce an executable.
相关文章:

深度学习 李沐报错
3.6. softmax回归的从零开始实现 — 动手学深度学习 2.0.0 documentation softmax从0开始实现 函数执行需要加main指定 改成这样 if __name__"__main__":print(evaluate_accuracy(net, test_iter)) 不然会这样出错 RuntimeError: An attempt has been m…...

【JAVA程序设计】(C00104)基于Springboot的家庭理财管理系统——有文档
基于Springboot的家庭理财管理系统项目简介项目获取开发环境项目技术运行截图运行视频项目简介 基于Springboot开发的家庭理财管理系统设计与实现共分为三个角色:系统管理员、家庭管理员、家庭用户 管理员角色包含以下功能: 用户管理、修改密码、角色管…...
【第五章 AOP概述,底层原理,AOP术语,切入点表达式,AOP操作(基于注解方式,基于xml配置文件)】
第五章 AOP概述,底层原理,AOP术语,切入点表达式,AOP操作(基于注解方式,基于xml配置文件) 1.AOP概述: (1)什么是AOP: ①面向切面编程(…...
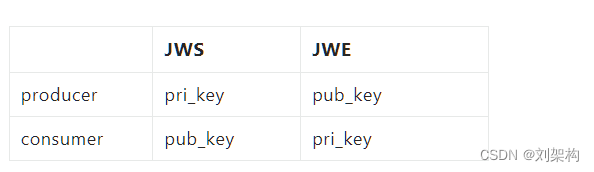
面试官: 你知道 JWT、JWE、JWS 、JWK嘛?
想起了 之前做过的 很多 登录授权 的项目 它相比原先的session、cookie来说,更快更安全,跨域也不再是问题,更关键的是更加优雅 ,所以今天总结了一篇文章来介绍他 JWT 指JSON Web Token,如果在项目中通过 jjwt 来支持 J…...
基于企业微信应用消息的每日早安推送
基于企业微信应用消息的每日早安推送 第一步:注册企业微信 企业微信注册地址:https://work.weixin.qq.com/wework_admin/register_wx 按照正常流程填写信息即可,个人也可以注册企业微信,不需要公司 注册完成后,登录…...
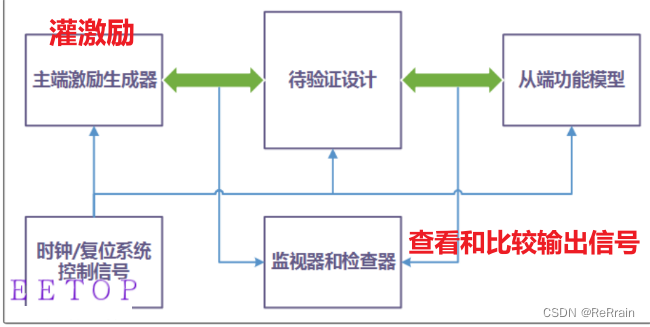
【数字IC基础】黑盒验证、白盒验证、 灰盒验证
文章目录 一、黑盒验证二、白盒验证三、灰盒验证一、黑盒验证 1、黑盒验证:大多数基于仿真的验证环境都是黑盒验证;2、不需要知道设计的内部结构和特性,只需要在输入端口打激励,观察输出即可;3、验证工程师学习设计的规格,然后编写验证环境中的 drivers, monitors, check…...

管理的本质是达成目标
“没有目标,其实就没有管理学存在的意义。要有效地使用管理学的智慧,首先要建立清晰的目标。” - 《宁向东的管理学课》 起源 最近开始刷很久之前就在得到上买了的已经起灰了的课程,看到这句话觉得很有道理。 思考 这里面有一个很重要的词…...
常用缩写)
【数字IC基础】IC(Integrated Circuit,集成电路)常用缩写
文章目录 1、集成电路:2、数字IC设计相关步骤:3、数字设计相关概念:4、验证相关:5、语言类:6、IC设计相关工具:7、存储器相关:8、总线协议类:9、文件格式类:10、标准和规范:11、其它:1、集成电路: 缩写全称中文翻译LSILarge-scale intergrated circuit大规模集成电…...
JavaScript 高级1 :面向对象
JavaScript 高级1 :面向对象 Date: January 16, 2023 Text: 面向对象、ES6中类和对象、类的继承、面向对象案例 目标: 能够说出什么是面向对象 能够说出类和对象的关系 能够使用 class 创建自定义类型 能够说出什么是继承 面向对象编程介绍 面向过…...
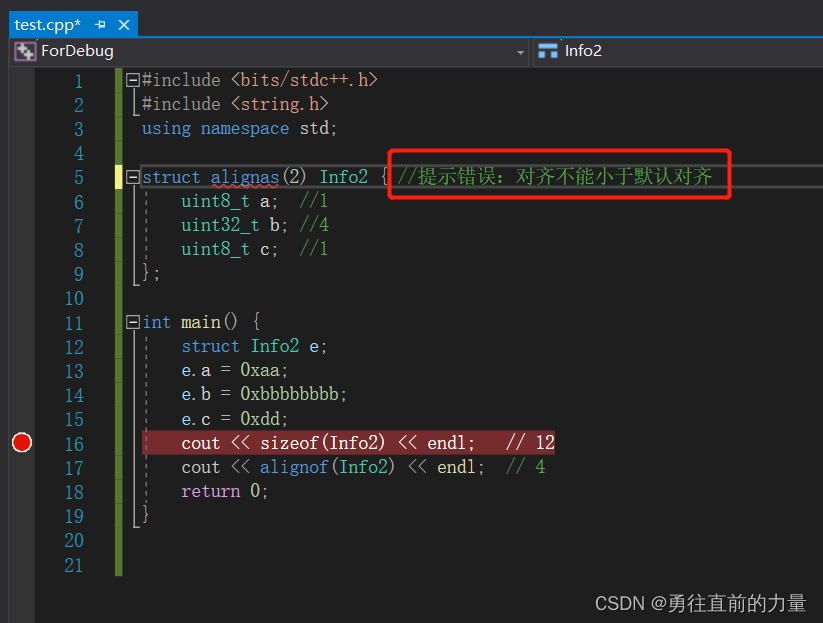
C语言结构体对齐
1. 结构体对齐 要点 变量只能存储在他的长度的整数倍地址上结构体整体对齐跟他的最长的字段整数倍对齐 栗子1 struct Example1 {char a; //1个字节int c; //4个字节short b; //2个字节 };std::cout << sizeof(Example1 ) << std::endl; // 12 std::cout &…...
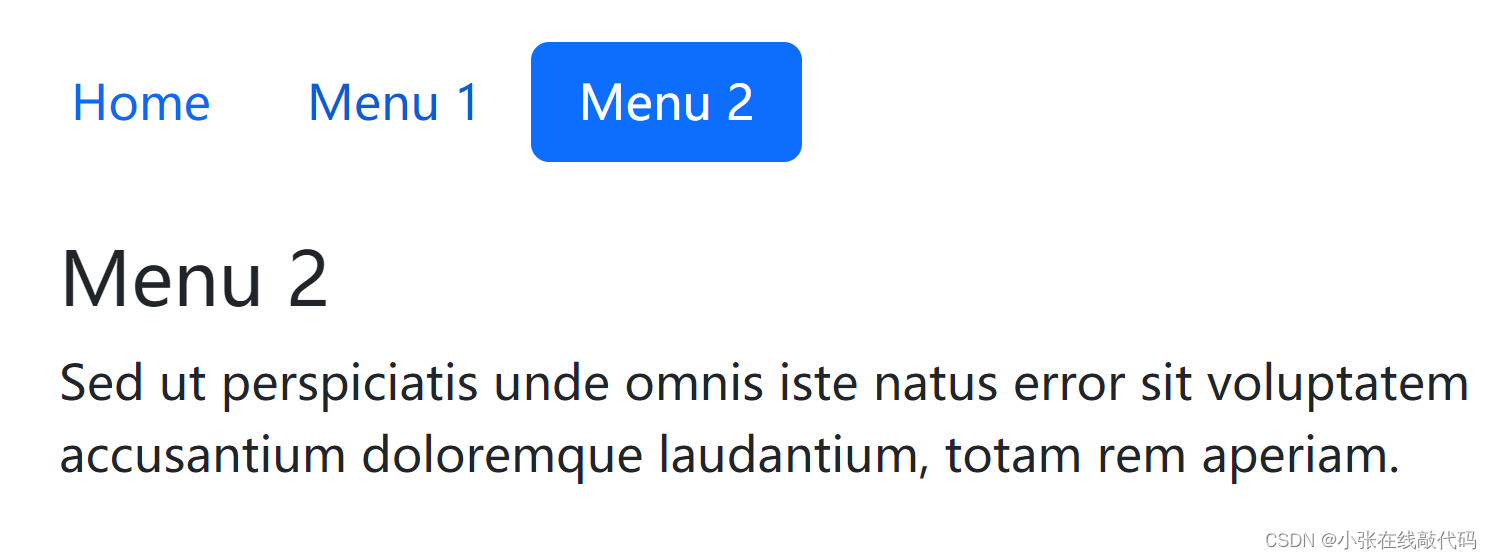
Bootstrap系列之导航
Bootstrap导航 可以在 ul 元素上添加 .nav类,在每个 li 选项上添加 .nav-item 类,在每个链接上添加 .nav-link 类: 基本的导航 <div class"container mt-3"><h2>导航</h2><p>简单的水平导航:</p><ul class&…...
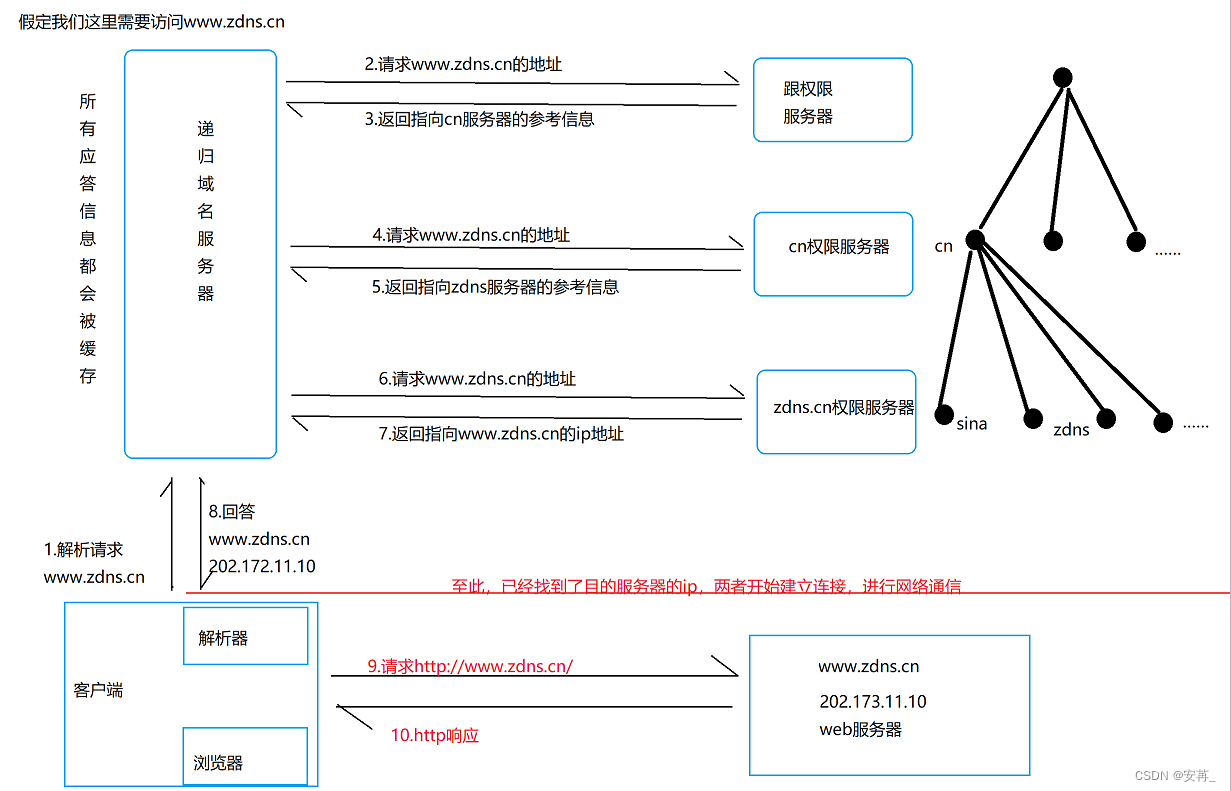
Java EE|TCP/IP协议栈之应用层协议DNS详解
文章目录一、对DNS的感性认识简介特点一些常见疑问二、DNSDNS域名结构域名的分级三、域名服务器四、域名解析过程参考一、对DNS的感性认识 简介 DNS,即Domain Name System,是域名系统的简称。它是Internet上解决网上机器命名的一种系统。 TCP/IP中的IP地址是由四…...
)
【MyBatis】作用域生命周期(四)
🚗MyBatis学习第四站~ 🚩起始站:MyBatis概述&环境搭建(一) 🚩本文已收录至专栏:数据库学习之旅 👍希望您能有所收获 一.引入 为了使用方便,我们经常能看到各种教程都将MyBatis抽离为工具类…...
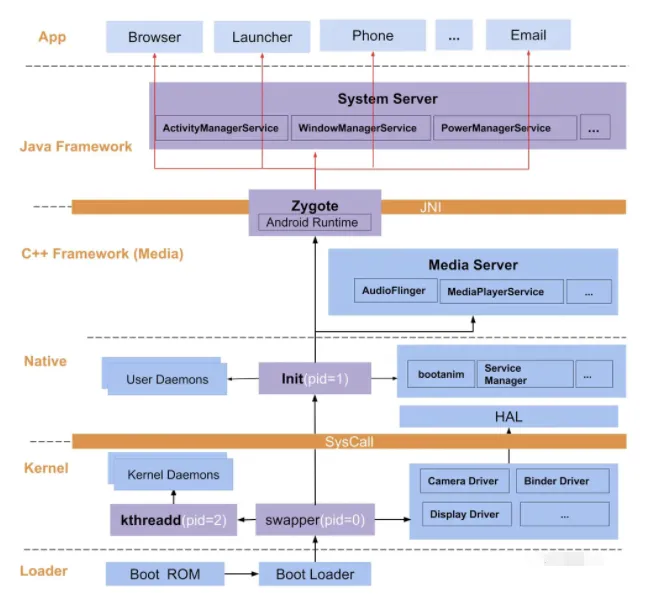
腾讯一面—Android 系统启动流程详解
正文AMS 是 Android 中最核心的服务之一,主要负责系统中四大组件的启动、切换、调度及应用进程的管理和调度等工作,其职责与操作系统中的进程管理和调度模块相类似,它本身也是一个 Binder 的实现类,应用进程能通过 Binder 机制调用…...
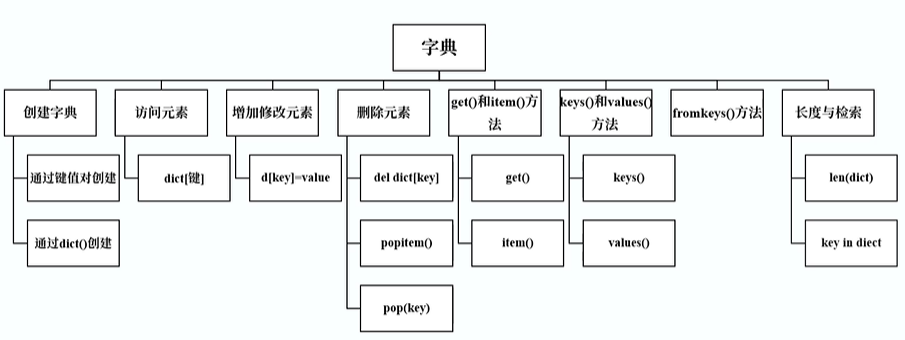
【Python知识点桂电版】02组合数据类型
一、序列序列简介序列是指一种包含多项数据的数据结构,分为不可变序列和可变序列。可变序列可修改序列内的元素如列表,二不可变序列一旦建立就不能修改其中的元素,字符串和元组属于不可变序列。列表和元组的创建列表:列表名 [元素…...
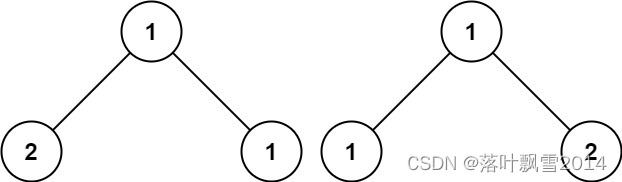
LeetCode100_100. 相同的树
LeetCode100_100. 相同的树 一、描述 给你两棵二叉树的根节点 p 和 q ,编写一个函数来检验这两棵树是否相同。 如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。 示例 1: 输入:p [1,2,3], q […...

javaEE 初阶 — 网络层中 IP 协议 的报文结构
文章目录IP 协议报文4位版本号4位首部长度8位服务类型16位总长度(字节数)8位生存时间(TTL)与 8位协议16位首部校验和32位源 IP 地址与32位目标 IP 地址动态分配的 IP 地址NAT 网络地址转换IPv6IP 协议报文 4位版本号 这里的 IP 协…...

iOS swift UICollectionView
文章目录1.纯代码自定义UICollectionViewCell2.禁止滑动(弹簧效果)3.UICollectionView的长按拖动2.在一个控制器中放两个UICollectionView或者UITableView,代理方法要怎么写1.纯代码自定义UICollectionViewCell import UIKitclass NewDeviceBottomColle…...

计算机三级数据库 填空题汇总
计算机三级 数据库 IDEF0需求建模方法由箭头和(活动/方框/矩形)两种元素构成。、从安全性角度考虑,防火墙技术是用来保证数据库应用系统的(网络)环境安全的。在UML的状态机图中,状态之间的转移是由&#x…...
【Java学习】初识Java
JavaSEJava初识1. Java简介2.Java环境的安装与配置3. 开发第一个Java程序Java初识 学前疑问:(带着疑问去学习,在学习中自行探索答案) Java是什么?能做什么?发展前景如何?需要学习哪些内容&…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...

提升移动端网页调试效率:WebDebugX 与常见工具组合实践
在日常移动端开发中,网页调试始终是一个高频但又极具挑战的环节。尤其在面对 iOS 与 Android 的混合技术栈、各种设备差异化行为时,开发者迫切需要一套高效、可靠且跨平台的调试方案。过去,我们或多或少使用过 Chrome DevTools、Remote Debug…...

热门Chrome扩展程序存在明文传输风险,用户隐私安全受威胁
赛门铁克威胁猎手团队最新报告披露,数款拥有数百万活跃用户的Chrome扩展程序正在通过未加密的HTTP连接静默泄露用户敏感数据,严重威胁用户隐私安全。 知名扩展程序存在明文传输风险 尽管宣称提供安全浏览、数据分析或便捷界面等功能,但SEMR…...
