算法题:870. 优势洗牌
该算法是临时想出来的,Java代码的实现在时间上不占优,之后有时间要优化一下,目前就是给大家提供一下思路。

解题思路:田忌赛马的思想 + 贪心法。
Step1. 对两个数组进行排序。
Step2. 同时遍历排序后的nums2和nums1,将num1中刚好超过nums2当前值的值放到对应的位置,而不超过nums2当前值的值放到最后面去,因为反正这些值超不过nums2,不如把num1中较小的值用来对应nums2中较大的值。
Java代码
import java.util.Arrays;
import java.util.Comparator;
import java.util.stream.IntStream;public class AdvantageCount {public static void main(String[] args) {Solution sol = new Solution();System.out.println(Arrays.toString(sol.advantageCount(new int[]{2,7,11,15}, new int[]{1,10,4,11})));System.out.println(Arrays.toString(sol.advantageCount(new int[]{12,24,8,32}, new int[]{13,25,32,11})));}
}class ArrayIndexComparator implements Comparator<Integer> {private final Integer[] A;public ArrayIndexComparator(Integer[] arr) {this.A = arr;}public int compare(Integer o1, Integer o2) {return A[o1].compareTo(A[o2]);}
}class Solution {public int[] advantageCount(int[] nums1, int[] nums2) {int n = nums1.length;// int[] -> Integer[]Integer[] nums2Integers = Arrays.stream(nums2).boxed().toArray(Integer[]::new);// 排序后返回原索引Integer[] nums2Indexs = new Integer[n];IntStream.range(0, n).forEach(val -> nums2Indexs[val] = val);Arrays.sort(nums2Indexs, new ArrayIndexComparator(nums2Integers));int[] new_nums1 = new int[n];Arrays.sort(nums1);int j = 0;int k = n - 1;for (int i = 0; i < n; i++) {while(j < n && nums1[j] <= nums2[nums2Indexs[i]]){new_nums1[nums2Indexs[k]] = nums1[j];k--;j++;}if(j < n){new_nums1[nums2Indexs[i]] = nums1[j];j++;}}return new_nums1;}
}完整题目
870. 优势洗牌
给定两个长度相等的数组 nums1 和 nums2,nums1 相对于 nums2 的优势可以用满足 nums1[i] > nums2[i] 的索引 i 的数目来描述。
返回 nums1 的任意排列,使其相对于 nums2 的优势最大化。
示例 1:
输入:nums1 = [2,7,11,15], nums2 = [1,10,4,11]
输出:[2,11,7,15]
示例 2:
输入:nums1 = [12,24,8,32], nums2 = [13,25,32,11]
输出:[24,32,8,12]
提示:
1 <= nums1.length <= 10^5nums2.length == nums1.length0 <= nums1[i], nums2[i] <= 10^9
相关文章:

算法题:870. 优势洗牌
该算法是临时想出来的,Java代码的实现在时间上不占优,之后有时间要优化一下,目前就是给大家提供一下思路。 解题思路:田忌赛马的思想 贪心法。 Step1. 对两个数组进行排序。 Step2. 同时遍历排序后的nums2和nums1,将…...

[架构之路-252/创业之路-83]:目标系统 - 纵向分层 - 企业信息化的呈现形态:常见企业信息化软件系统 - 企业应用信息系统集成
目录 第一章 什么是企业应用信息系统集成What 1.1 简介 1.2 架构 二、为什么需要企业应用信息系统集成Why 三、如何实现企业应用信息系统集成 3.1 步骤 3.2 企业应用集成的层次 3.3 业务流程重组 第一章 什么是企业应用信息系统集成What 1.1 简介 企业应用信息系统集…...

MFC发送http https以及json解析
域名解析成IP char szWeb[128] "www.baidu.com";struct hostent *pHost NULL;pHost gethostbyname(szWeb);//完成主机名到域名的解析char *IP inet_ntoa(*((struct in_addr *)pHost->h_addr));CString ipStr IP;请求三部曲: 1、CInternetSession…...
UE5加载websocket模块为空
今天测试UE 发现工程启动不了,后来看到原来是websocket模块无法加载。 解决的它的方法很简单,这种问题一般会出现在源码版本的引擎或者是停电了,导致UElaunch版本损坏,解决方法是来到源码版本的引擎 这个目录下: D:\…...

学习 Python 数据可视化,如何快速入门?
Python 是一种非常流行的编程语言,具有简单易学、高效、丰富的库和工具等特点。其中,数据可视化是 Python 的一个重要应用领域,可以帮助人们更好地理解和分析数据。本文将介绍如何快速入门 Python 数据可视化,以及常用的可视化工具…...

XUbuntu22.04之simplenote支持的Markdown语法总结(一百九十一)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 人生格言: 人生…...

JAVA深化篇_26——Apache commons-io工具包的使用
Apache commons-io工具包的使用 Apache基金会介绍 Apache软件基金会(也就是Apache Software Foundation,简称为ASF),是专门为支持开源软件项目而办的一个非盈利性组织。在它所支持的Apache项目与子项目中,所发行的软…...

centos 7 kafka2.6单机安装及动态认证SASL SCRAM配置
目录 1.kfaka安装篇 1.1 安装jdk 1.2安装kafka 2.安全篇 2.1 kafka安全涉及3部份: 2.2 Kafka权限控制认证方式 2.3 SASL/SCRAM-SHA-256 配置实例 2.3.1 创建用户 2.3.2 创建 JAAS 文件及配置 3.测试 3.1 创建测试用户 3.2 配置JAAS 文件 3.2.1 生产者配…...
TrafficWatch 数据包嗅探器工具
TrafficWatch 是一种数据包嗅探器工具,允许您监视和分析 PCAP 文件中的网络流量。它提供了对各种网络协议的深入了解,并可以帮助进行网络故障排除、安全分析等。 针对 ARP、ICMP、TCP、UDP、DNS、DHCP、HTTP、SNMP、LLMNR 和 NetBIOS 的特定于协议的数据…...
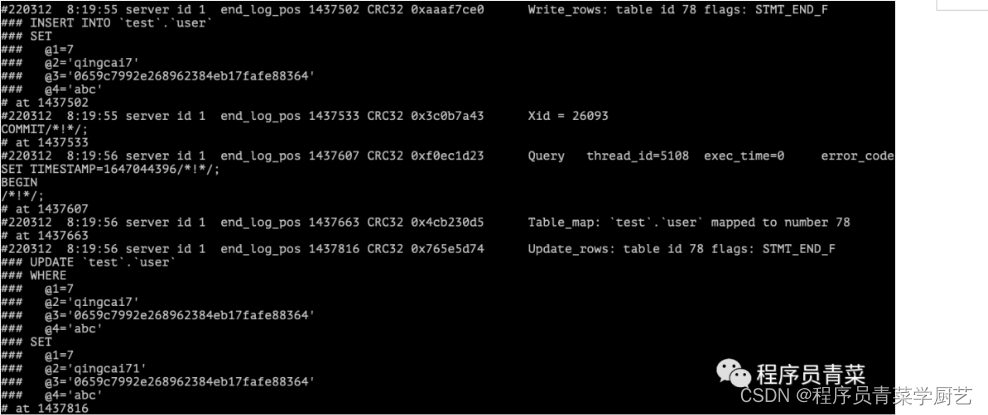
MySQL Binlog实战应用之一
一、前言 开发业务系统尤其是与财务相关的系统,需要记录每一笔变更操作的日志,这一般有两种实现方案。 1、代码中通过AOP实现,提供注解跟踪记录日志,这种方案能够比较清晰地以业务角度记录操作日志,但记录变更前的旧…...

【MySQL】MVCC机制(undo log,read view)
文章目录 前言一. 预备知识二. 模拟MVCC三. Read View四. RC与RR的本质区别结束语 前言 MVCC(多版本并发控制)是一种用来解决读-写冲突的无锁并发控制 MVCC为事务分配单向增长的事务ID,为每个修改保存一个版本,版本与事物ID相关联…...
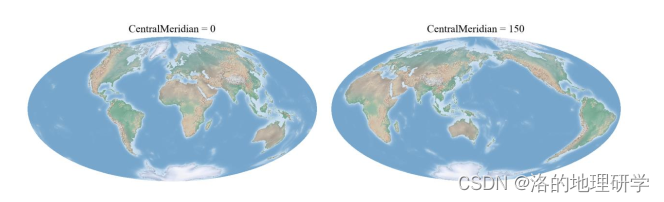
gma 2 教程(三)坐标参考系统:3.投影方法
安装 gma:pip install gma 地图投影是利用一定数学法则把地球表面的经、纬线转换到平面上的理论和方法。由于地球是一个赤道略宽两极略扁的不规则的梨形球体,故其表面是一个不可展平的曲面,所以运用任何数学方法进行这种转换都会产生误差和变…...

蓝桥杯每日一题2023.11.2
题目描述 等差素数列 - 蓝桥云课 (lanqiao.cn) 题目分析 对于此题我们需要求出最小的公差并且长度为10, 1.确保序列开始为素数 2.确定枚举的个数 注意:序列中数只是d的变化,可以通过此计算将开始数字后9个数字都计算出来,d是…...

Leetcode67二进制求和
1104 代码: class Solution {public String addBinary(String a, String b) {StringBuffer ans new StringBuffer();int n Math.max(a.length(),b.length()),carry 0;for(int i0;i<n;i){carry i < a.length()?(a.charAt(a.length()-1-i)-0):0;carry i…...
线性代数 第五章 特征值与特征向量
一、特征值定义 二、特征值求法 定义法;;相似。 三、特征向量求法 定义法;基础解系法;;相似。 四、特征值性质 不同特征值的特征向量线性无关k重特征值至多有k个线性无关的特征向量 五、相似的定义 若ÿ…...
(python数据库))
Python嵌入式数据库 / 轻量级数据库 / 小型数据库介绍(SQLite、Pandas DataFrame、TinyDB)(python数据库)
文章目录 Python嵌入式数据库/轻量级数据库介绍什么是嵌入式数据库/轻量级数据库?SQLitePandasTinyDB总结 Python嵌入式数据库/轻量级数据库介绍 在构建应用程序时,数据存储是必不可少的一部分。传统的方式是使用如MySQL、PostgreSQL这样的重量级数据库…...

USB PD v1.0快速充电通信原理
1 原理 本篇文章讲的快速充电是指USB论坛所发布的USB Power Delivery快速充电规范(通过VBUS直流电平上耦合FSK信号来请求充电器调整输出电压和电流的过程),不同于本人发布的另一篇文章所讲的高通Quick Charger 2.0规范,因为高通QC…...
【华为】路由器以PPPoE拨号接入广域网
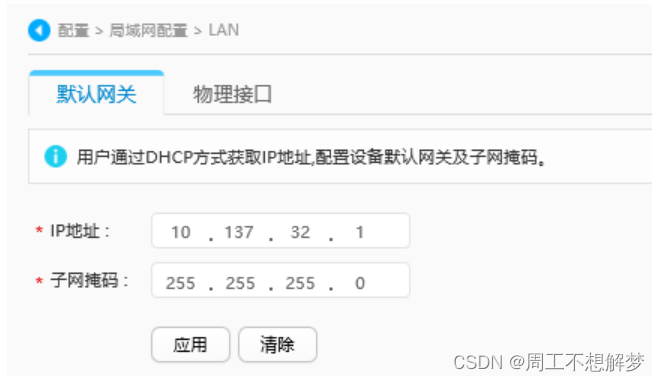
组网需求 用户希望以PPPoE拨号方式接入广域网,如图1所示,Router作为PPPoE客户端,得到PPPoE服务器的认证后获得IP地址,实现用户接入互联网的需求。内网网关地址(即VLANIF1接口的IP地址)为10.137.32.1/24。 …...
--内核架构和子系统)
Linux内核分析(一)--内核架构和子系统
目录 一、引言 二、内核架构 ------>2.1、kernel源码获取 ------>2.2、cpuinfo ------>2.3、内核体系结构 ------>2.4、内核主要组件 三、内核源码及子系统 ------>3.1、整体结构与子系统 ------>3.2、cpuinfo ------>3.3、整体结构与子系统 -…...
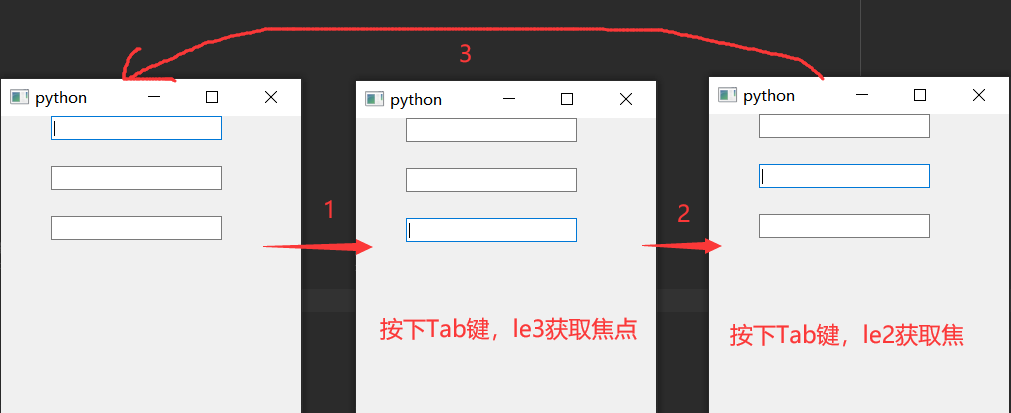
【PyQt学习篇 · ⑨】:QWidget -控件交互
文章目录 是否可用是否显示/隐藏是否编辑是否为活跃窗口关闭综合案例信息提示状态提示工具提示“这是什么”提示 焦点控制单个控件角度父控件角度 是否可用 setEnabled(bool):该函数用于设置QWidget控件的可用性,参数bool为True表示该控件为可用状态&…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...

第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10+pip3.10)
第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10pip3.10) 一:前言二:安装编译依赖二:安装Python3.10三:安装PIP3.10四:安装Paddlepaddle基础框架4.1…...

Win系统权限提升篇UAC绕过DLL劫持未引号路径可控服务全检项目
应用场景: 1、常规某个机器被钓鱼后门攻击后,我们需要做更高权限操作或权限维持等。 2、内网域中某个机器被钓鱼后门攻击后,我们需要对后续内网域做安全测试。 #Win10&11-BypassUAC自动提权-MSF&UACME 为了远程执行目标的exe或者b…...
