当前位置：首页 > news >正文

线性代数第五章特征值与特征向量

news 2026/2/8 15:22:42

一、特征值定义

$A\alpha =\lambda \alpha ,a\neq 0$

二、特征值求法

定义法；
$\left | \lambda E-A \right |=0$ ；
相似。

三、特征向量求法

定义法；
基础解系法；
$(\lambda E-A)x=0$ ；
相似。

四、特征值性质

不同特征值的特征向量线性无关
k重特征值至多有k个线性无关的特征向量
$\left | A \right |=\prod \lambda _i,\sum a_{ii}=\sum \lambda _i$

五、相似的定义

若 $P^{-1}AP=B$ ，则A和B相似。

六、相似的性质（必要条件）

$r(A)=r(B)$
$\left | A \right |=\left | B \right |$
$\left | \lambda E-A \right |=\left | \lambda E-B \right |$
$\sum a_{ii}=\sum b_{ii}$

七、可对角化

7.1 充要条件

A有n个线性无关的特征向量
如果λ是k重特征值，那么λ必有k个线性无关的特征向量
$r(\lambda _i E-A)=n-n_i,\lambda _i$ 为 $n_i$ 重特征值

7.2 充分条件

A有n个不同的特征值
A是实对称矩阵

八、实对称矩阵隐含的信息

必与对角矩阵相似
可用正交矩阵对角化，且对角阵上的元素即为特征值
不同特征值的特征向量必正交
特征值必是实数，特征向量必是实向量
k重特征值必有k个线性无关的特征向量（ $r(\lambda E-A)=n-k$ ）
n阶实对称矩阵A有n个特征值的话（含重根），若r(A)<n，则有n-r(A)个零特征值
秩等于非零特征值的个数

$P_1^{-1}AP_1=B,P_2^{-1}BP_2=C\Rightarrow P^{-1}AP=C,P=P_1P_2$

$A$	$kA+E$	$A+kE$	$A^{-1}$	$A^*$	$A^n$	$P^{-1}AP$
$\lambda$	$k\lambda +1$	$\lambda +k$	$\frac{1}{\lambda }$	$\frac{\left \| A \right \|}{\lambda }$	$\lambda ^n$	$\lambda$
$\alpha$	$\alpha$	$\alpha$	$\alpha$	$\alpha$	$\alpha$	$P^{-1}\alpha$

线性代数第五章特征值与特征向量

一、特征值定义二、特征值求法定义法；；相似。三、特征向量求法定义法；基础解系法；；相似。四、特征值性质不同特征值的特征向量线性无关k重特征值至多有k个线性无关的特征向量五、相似的定义若&#xff…...

编程日记 2023/11/4 6:38:24

Python嵌入式数据库 / 轻量级数据库 / 小型数据库介绍（SQLite、Pandas DataFrame、TinyDB）（python数据库）

文章目录 Python嵌入式数据库/轻量级数据库介绍什么是嵌入式数据库/轻量级数据库？SQLitePandasTinyDB总结 Python嵌入式数据库/轻量级数据库介绍在构建应用程序时，数据存储是必不可少的一部分。传统的方式是使用如MySQL、PostgreSQL这样的重量级数据库…...

编程日记 2023/11/4 6:37:23

USB PD v1.0快速充电通信原理

1 原理本篇文章讲的快速充电是指USB论坛所发布的USB Power Delivery快速充电规范（通过VBUS直流电平上耦合FSK信号来请求充电器调整输出电压和电流的过程），不同于本人发布的另一篇文章所讲的高通Quick Charger 2.0规范，因为高通QC…...

编程日记 2023/11/4 6:36:22

【华为】路由器以PPPoE拨号接入广域网

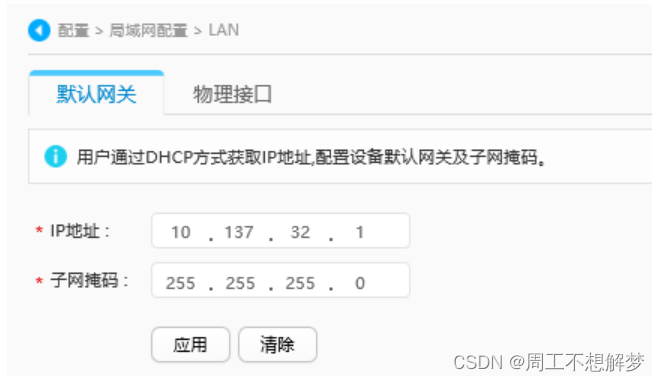
组网需求用户希望以PPPoE拨号方式接入广域网，如图1所示，Router作为PPPoE客户端，得到PPPoE服务器的认证后获得IP地址，实现用户接入互联网的需求。内网网关地址（即VLANIF1接口的IP地址）为10.137.32.1/24。 …...

编程日记 2023/11/4 6:35:20

Linux内核分析(一)--内核架构和子系统

目录一、引言二、内核架构 ------>2.1、kernel源码获取 ------>2.2、cpuinfo ------>2.3、内核体系结构 ------>2.4、内核主要组件三、内核源码及子系统 ------>3.1、整体结构与子系统 ------>3.2、cpuinfo ------>3.3、整体结构与子系统 -…...

编程日记 2023/11/4 6:34:19

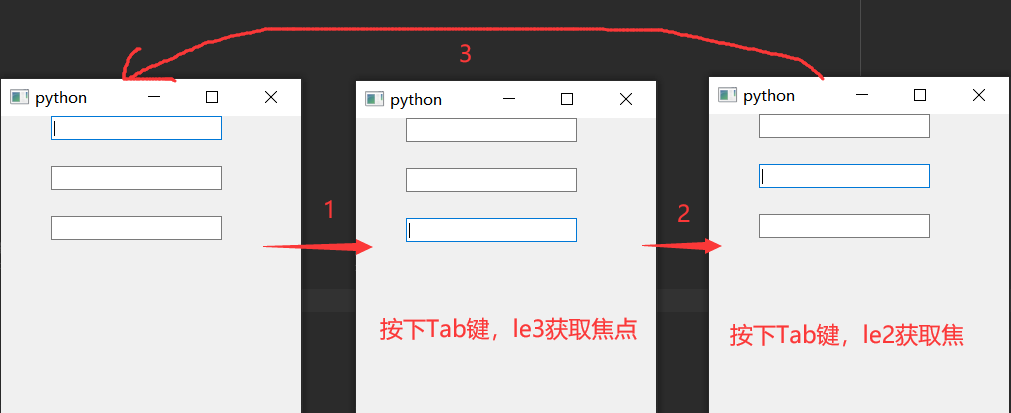
【PyQt学习篇 · ⑨】：QWidget -控件交互

文章目录是否可用是否显示/隐藏是否编辑是否为活跃窗口关闭综合案例信息提示状态提示工具提示“这是什么”提示焦点控制单个控件角度父控件角度是否可用 setEnabled(bool)：该函数用于设置QWidget控件的可用性，参数bool为True表示该控件为可用状态&…...

编程日记 2023/11/4 6:32:17

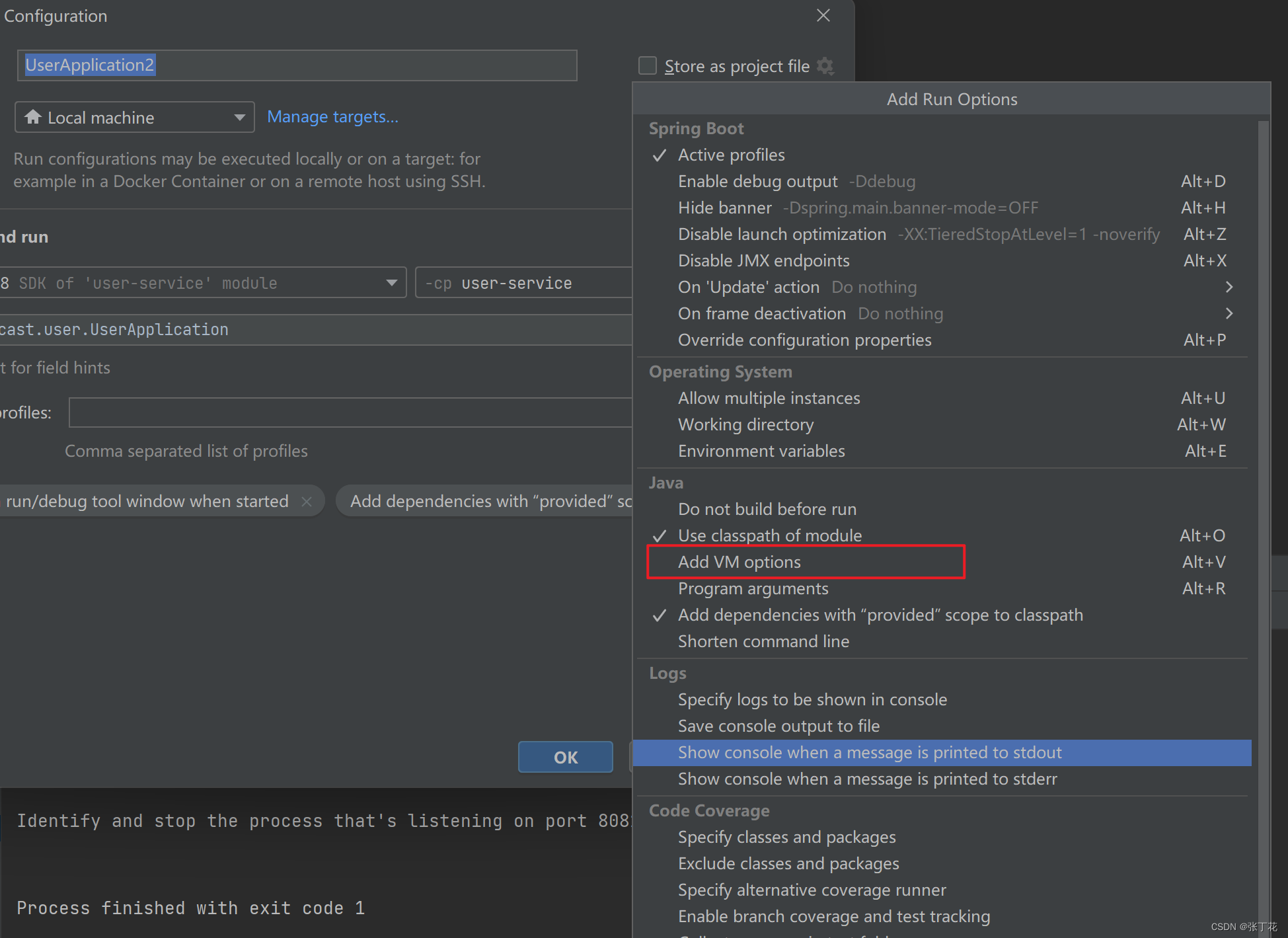
新版本IntelliJ IDEA（如2023）中运行Spring Boot找不到VM options进行端口的修改的问题解决

问题如下图找不到VM options。解决进行如下操作即可。...

编程日记 2023/11/4 6:31:16

Swift语言配合HTTP写的一个爬虫程序

下段代码使用Embassy库编写一个Swift爬虫程序来爬取jshk的内容。我会使用proxy_host为duoip，proxy_port为8000的爬虫IP服务器。使用Embassy库编写一个Swift爬虫程序可以实现从网页上抓取数据的功能。下面是一个简单的步骤： 1、首先，需要在X…...

编程日记 2023/11/4 6:28:12

前言本章介绍如何在linux开发板准备好了fb0的情况下移植lvgl。抓取源码 git clone https://github.com/lvgl/lvgl.git git clone https://github.com/lvgl/lv_drivers.git git clone https://github.com/lvgl/lv_demos.git git clone https://github.com/lvgl/lv_port_lin…...

编程日记 2023/11/4 6:26:09

C之(10)CMocka-单元测试框架使用

CMocka基础使用 Author：Once Day Date：2023年6月15日参考文档： GoogleTest User’s Guide | GoogleTest嵌入式自动化单元测试(2)-Cmocka - 知乎 (zhihu.com)使用 cmocka 进行单元测试 | 前尘逐梦 (qianchenzhumeng.github.io)cmocka - un…...

编程日记 2023/11/4 6:25:07

如何在idea中使用maven搭建tomcat环境

目录一、创建maven项目二、完善代码结构三、引入依赖和插件四、启动tomcat，运行项目 （1）点击添加配置 （2）点击左上角的加号，选择maven （3）输入运行命令五、验证一、创建…...

编程日记 2023/11/4 6:24:06

单点登录

单点登录（Single Sign-On，简称SSO）是一种可以让用户在多个应用程序和网站中使用同一组登录凭证的技术，即用户只需通过一次身份验证，就可以访问多个应用和网站。以下是单点登录的相关知识点： 1. 身份验证机…...

编程日记 2023/11/4 6:23:05

大数据(十)：数据可视化(二)

专栏介绍结合自身经验和内部资料总结的Python教程，每天3-5章，最短1个月就能全方位的完成Python的学习并进行实战开发，学完了定能成为大佬！加油吧！卷起来！ 全部文章请访问专栏：《Python全栈教…...

编程日记 2023/11/4 6:22:04

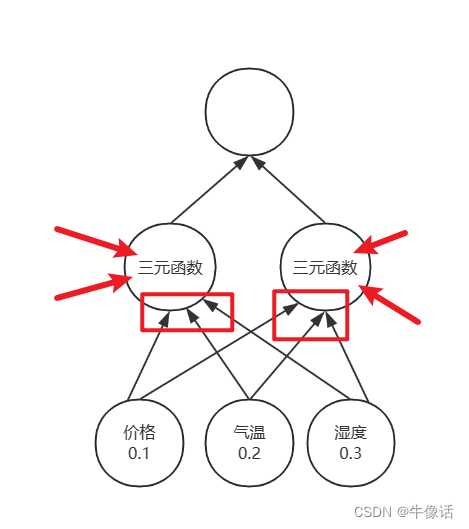
pytorch+LSTM实现使用单参数预测，以及多参数预测（代码注释版）

开发前准备： 环境管理：Anaconda python: 3.8 显卡：NVIDIA3060 pytorch: 到官网选择conda版本，使用的是CUDA11.8 编译器： PyCharm 简述： 本次使用seaborn库中的flights数据集来做试验，我们通过…...

编程日记 2023/11/4 6:20:03

腾讯云3年/5年特惠云服务器购买入口及攻略

腾讯云是腾讯旗下云计算品牌，为了吸引用户经常推出各种优惠活动，最吸引用户的还是特惠云服务器，下面给大家分享腾讯云3年/5年时长特惠服务器购买入口及教程！ 购买入口：传送门>>> 购买攻略： 进入…...

编程日记 2023/11/4 6:19:02

【Linux】jdk Tomcat MySql的安装及Linux后端接口部署

一，jdk安装 1.1 上传安装包到服务器打开MobaXterm通过Linux地址连接到Linux并登入Linux，再将主机中的配置文件复制到MobaXterm 使用命令查看：ll 1.2 解压对应的安装包解压jdk 解压命令：tar -xvf jdk 加键盘中Tab键即可…...

编程日记 2023/11/4 6:18:01

天空卫士为集度智能汽车系上“安全带”

10月27日，集度汽车在北京正式发布了旗下首款量产车型——极越 01 SUV。极越 01 SUV 是一款集科技、智能、美学于一身的纯电动中大型SUV，号称全球首款“AI 汽车机器人”。作为集度的合作伙伴，天空卫士第一时间送上祝福，祝愿极越大卖…...

编程日记 2023/11/4 6:16:58

vue el-table-column 修改一整列的背景颜色

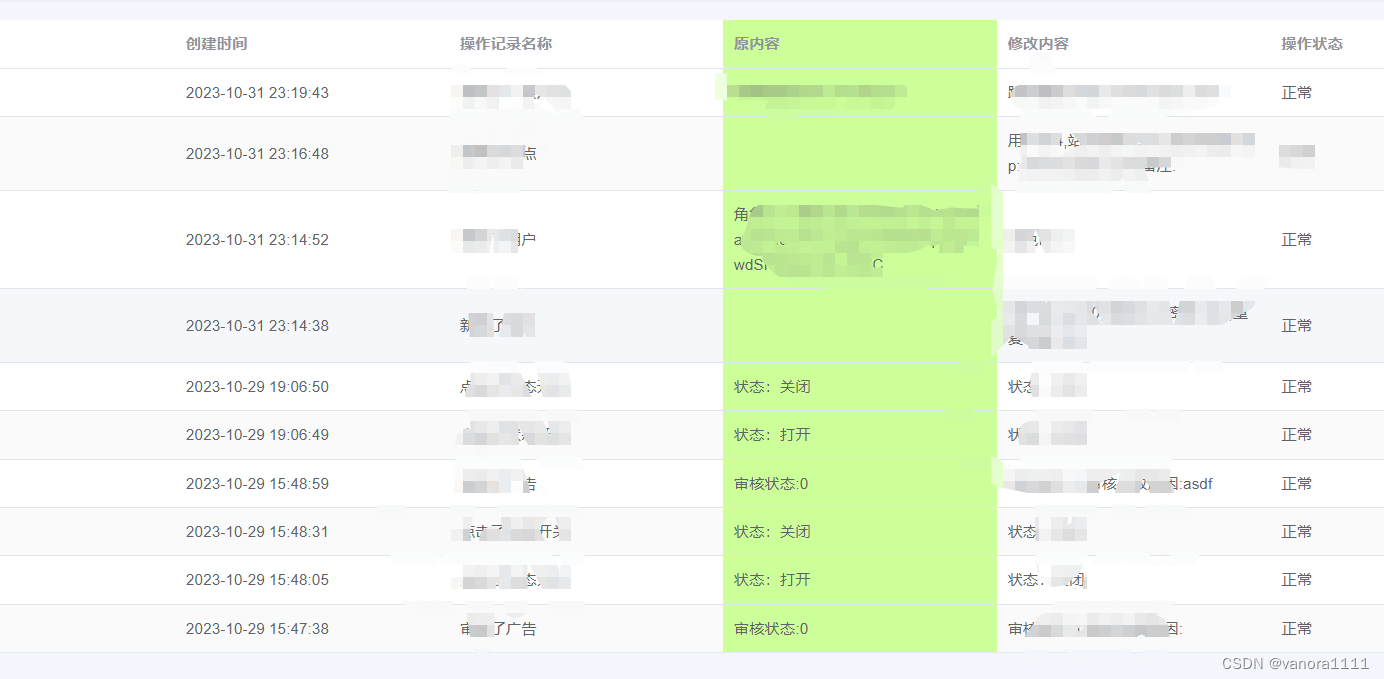
目录修改表头以及一整列数据的背景颜色，效果如下： 总结修改表头以及一整列数据的背景颜色，效果如下： 修改表头背景颜色：在el-table绑定header-cell-style 修改一整列的数据背景颜色：在el-table绑定:cel…...

编程日记 2023/11/4 6:15:57

docker 安装 minio (单体架构)

文字归档：https://www.yuque.com/u27599042/coding_star/qcsmgom7basm6y64 查询 minio 镜像 docker search minio拉取镜像 docker pull minio/minio创建启动 minio 容器用户名长度至少为 3，密码长度至少为 8 docker run \ -p 9000:9000 \ -p 9090:909…...

编程日记 2023/11/4 6:14:56

docker搭建kafka

1.拉取zookeeper镜像注意：云服务器需要设置安全策略放行2181与9092端口，否则访问失败 #默认拉取最新版本镜像 docker pull wurstmeister/zookeeper#检查镜像是否拉取成功 docker images | grep zookeeper2.通过docker运行zookeeper #docker容器单机启…...

编程日记 2023/11/4 6:13:54

深入剖析AI大模型：大模型时代的 Prompt 工程全解析

今天聊的内容，我认为是AI开发里面非常重要的内容。它在AI开发里无处不在，当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗"，或者让翻译模型 "将这段合同翻译成商务日语" 时，输入的这句话就是 Prompt。…...

编程新知 2026/2/7 5:56:30

突破不可导策略的训练难题：零阶优化与强化学习的深度嵌合

强化学习（Reinforcement Learning, RL）是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程，然后使用强化学习的Actor-Critic机制（中文译作“知行互动”机制），逐步迭代求解…...

编程新知 2026/2/5 4:17:42

STM32+rt-thread判断是否联网

一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

编程新知 2025/9/23 20:06:08

C++ 基础特性深度解析

目录引言一、命名空间（namespace） C 中的命名空间与 C 语言的对比二、缺省参数 C 中的缺省参数与 C 语言的对比三、引用（reference） C 中的引用与 C 语言的对比四、inline（内联函数…...

编程新知 2026/1/15 4:25:16

如何为服务器生成TLS证书

TLS（Transport Layer Security）证书是确保网络通信安全的重要手段，它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书，可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

编程新知 2025/12/17 5:54:30

WEB3全栈开发——面试专业技能点P2智能合约开发（Solidity）

一、Solidity合约开发下面是 Solidity 合约开发的概念、代码示例及讲解，适合用作学习或写简历项目背景说明。 🧠 一、概念简介：Solidity 合约开发 Solidity 是一种专门为以太坊（Ethereum）平台编写智能合约的高级编…...

编程新知 2026/1/27 9:33:09

分布式增量爬虫实现方案

之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面，避免重复抓取，以节省资源和时间。在分布式环境下，增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。另一种思路：将增量判…...

编程新知 2026/2/6 1:18:56

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”（装配）

船舶制造装配管理现状：装配工作依赖人工经验，装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书，但在实际执行中，工人对指导书的理解和遵循程度参差不齐。船舶装配过程中的挑战与需求挑战 (1…...

编程新知 2026/2/6 2:16:18

Java + Spring Boot + Mybatis 实现批量插入

在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法：使用 MyBatis 的 <foreach> 标签和批处理模式（ExecutorType.BATCH）。方法一：使用 XML 的 <foreach> 标签&#xff…...

编程新知 2025/6/11 2:44:05

保姆级教程：在无网络无显卡的Windows电脑的vscode本地部署deepseek

文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama（有网络的电脑）2.2.3 安装Ollama（无网络的电脑）2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

编程新知 2026/2/6 16:59:24