XCTF-RSA-2:baigeiRSA2、 cr4-poor-rsa
baigeiRSA2
题目描述
import libnum
from Crypto.Util import number
from functools import reduce
from secret import flagn = 5
size = 64
while True:ps = [number.getPrime(size) for _ in range(n)]if len(set(ps)) == n:breake = 65537
n = reduce(lambda x, y: x*y, ps)
m = libnum.s2n(flag)
c = pow(m, e, n)print('n = %d' % n)
print('c = %d' % c)n = 175797137276517400024170861198192089021253920489351812147043687817076482376379806063372376015921
c = 144009221781172353636339988896910912047726260759108847257566019412382083853598735817869933202168
分析解密
- 模数N不大,对其尝试分解,得到5个因子(P1,P2,P3,P4,P5)
- 题目中while循环生成了一个五元组ps
- n = reduce(lambda x, y: x*y, ps)
- reduce(function,iterable)对参数iterable进行function累积操作
- lambda匿名函数,在 lambda 关键字之后、冒号左边为参数列表,可不带参数,也可有多个参数。若有多个参数,则参数间用逗号隔开,冒号右边为 lambda 表达式的返回值。
- 因此n为ps里面元素的乘积,即 n = p s [ 1 ] ∗ p s [ 2 ] ∗ p s [ 3 ] ∗ p s [ 4 ] ∗ p s [ 5 ] = P 1 ∗ P 2 ∗ P 3 ∗ P 4 ∗ P 5 n=ps[1]*ps[2]*ps[3]*ps[4]*ps[5]=P1*P2*P3*P4*P5 n=ps[1]∗ps[2]∗ps[3]∗ps[4]∗ps[5]=P1∗P2∗P3∗P4∗P5
- 计算欧拉函数φ(n):
欧拉函数 φ(n) 的定义是小于等于 n 的正整数中与 n 互素的数的个数。
积的欧拉函数等于各个因子的欧拉函数之积。比如,φ(56)=φ(8×7)=φ(8)×φ(7)=4×6=24
因此此题中,根据因子都是素数,有
φ(n)=φ(P1*P2*P3*P4*P5)=φ(P1)*φ(P2)*φ(P3)*φ(P4)*φ(P5)=(P1-1)*(P2-1)*(P3-1)*(P4-1)*(P5-1) - 得到 φ(n) 后,即可计算私钥d,进行解密:
d和e在模数φ(n)下互为逆元:d = gmpy2.invert(e,phi)
m = c d m o d n c^d mod n cdmodn = pow(c,d,n) - 最后将明文m转换为字符串 libnum.n2s(int(m))
脚本如下
import gmpy2
import libnum
n = 175797137276517400024170861198192089021253920489351812147043687817076482376379806063372376015921
c = 144009221781172353636339988896910912047726260759108847257566019412382083853598735817869933202168
e = 65537
'''
循环生成了一个五元组ps
n = reduce(lambda x, y: x*y, ps)
reduce(function,iterable)对参数iterable进行function累积操作
lambda匿名函数,在 lambda 关键字之后、冒号左边为参数列表,可不带参数,也可有多个参数。若有多个参数,则参数间用逗号隔开,冒号右边为 lambda 表达式的返回值。
因此n为ps里面元素的乘积
'''
#分解n有:
P1 = 9401433281508038261
P2 = 13716847112310466417
P3 = 11215197893925590897
P4 = 10252499084912054759
P5 = 11855687732085186571#求欧拉函数φ(n)
#欧拉函数 φ(n) 的定义是小于等于 n 的正整数中与 n 互素的数的个数。
#积的欧拉函数等于各个因子的欧拉函数之积。比如,φ(56)=φ(8×7)=φ(8)×φ(7)=4×6=24
#因此此题中φ(n)=φ(P1*P2*P3*P4*P5)=φ(P1)*φ(P2)*φ(P3)*φ(P4)*φ(P5)=(P1-1)*(P2-1)*(P3-1)*(P4-1)*(P5-1),因子都是素数
phi = (P1-1)*(P2-1)*(P3-1)*(P4-1)*(P5-1)d = gmpy2.invert(e,phi)
m = pow(c,d,n)
print(libnum.n2s(int(m)))#b'HSCTF{@Tv0_br3ad5_c1ip_cHe3se_!@}'
cr4-poor-rsa
题目描述
 文件下载下来是一个.gz的压缩包,用Bandizip打开里面是密钥文件key.pub和flag文件flag.b64
文件下载下来是一个.gz的压缩包,用Bandizip打开里面是密钥文件key.pub和flag文件flag.b64
 !注意:不能就这样直接提取文件出来,得到的flag文件内容可能会出错。
!注意:不能就这样直接提取文件出来,得到的flag文件内容可能会出错。
正确的方式是将.gz补全后缀名,修改为.gz.tar压缩包,然后解压文件。
分析解密
- 对密钥pub文件提取n和e
哈哈我也不会,找了一下怎么打开key.pub文件
参考链接:https://blog.csdn.net/ChaoYue_miku/article/details/125749442
from Crypto.PublicKey import RSA
#获取密钥文件中的n和e
with open("./key.pub","rb") as file:key = file.read()
pub = RSA.importKey(key)
n = pub.n
e = pub.e
print("n=",n)
print("e=",e)
- 提取出n,e后,分解n得到p,q,然后可以计算私钥d
d = gmpy2.invert(e,(p-1)*(q-1)) - 提取密文后,解密flag:
生成私钥priv:rsa.PrivateKey(n,e,d,p,q)
先base64解密:base64.b64decode(cipher)
再rsa解密:rsa.decrypt(c,priv)
脚本如下:
from Crypto.PublicKey import RSA
import gmpy2
import base64
import rsa#获取密钥文件中的n和e
with open("./key.pub","rb") as file:key = file.read()
pub = RSA.importKey(key)
n = pub.n
e = pub.e
print("n=",n)
print("e=",e)
'''
#n= 833810193564967701912362955539789451139872863794534923259743419423089229206473091408403560311191545764221310666338878019
#e= 65537
'''#分解n,计算d
p = 863653476616376575308866344984576466644942572246900013156919
q = 965445304326998194798282228842484732438457170595999523426901
d = gmpy2.invert(e,(p-1)*(q-1))
print("d=",d)'''
根据n,e,d,p,q生成私钥,进行解密
先base64解密,再rsa解密
'''
priv = rsa.PrivateKey(n,e,d,p,q) #生成私钥
with open("./flag.b64","rb") as file: #提取密文cipher cipher = file.read()
print("cipher=",cipher)
c = base64.b64decode(cipher) #base64解密
flag = rsa.decrypt(c,priv).decode() #rsa解密
print("flag=",flag)#flag= ALEXCTF{SMALL_PRIMES_ARE_BAD}
相关文章:

XCTF-RSA-2:baigeiRSA2、 cr4-poor-rsa
baigeiRSA2 题目描述 import libnum from Crypto.Util import number from functools import reduce from secret import flagn 5 size 64 while True:ps [number.getPrime(size) for _ in range(n)]if len(set(ps)) n:breake 65537 n reduce(lambda x, y: x*y, ps) m …...
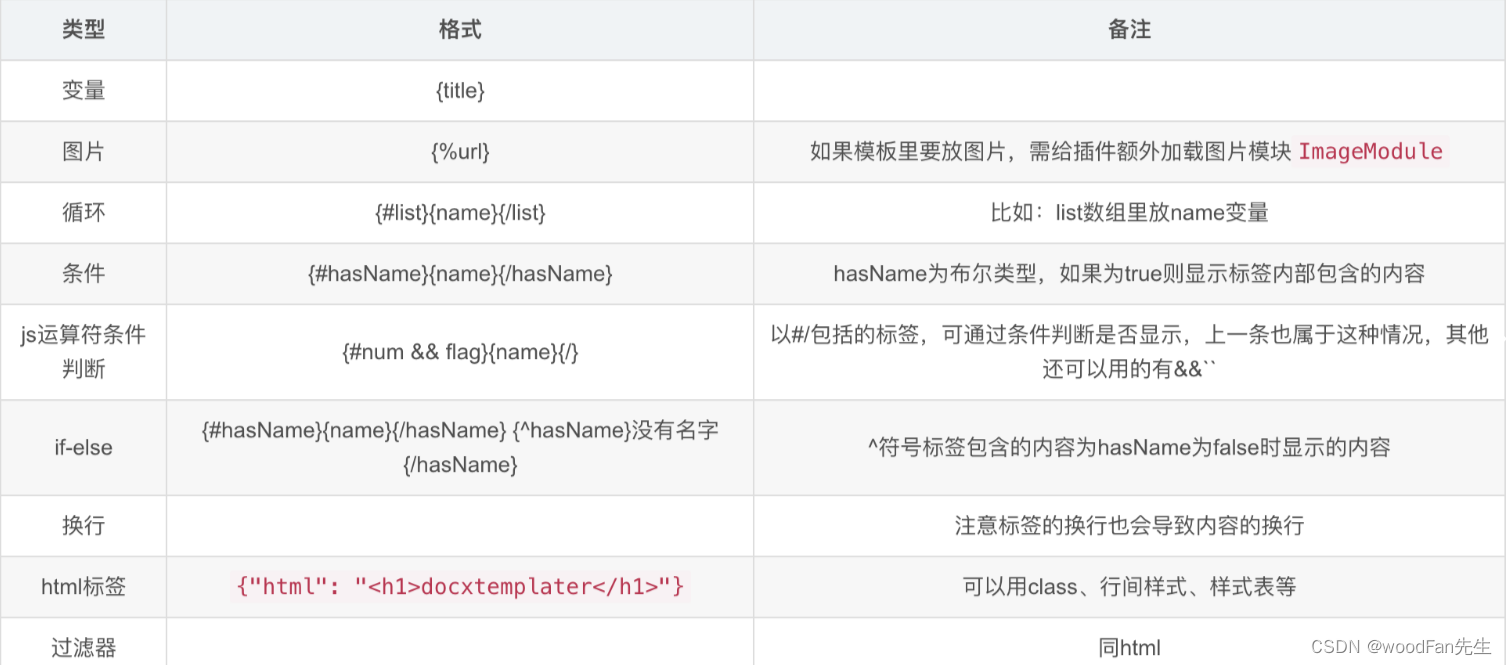
js 根据word文档模板导出内容
一、创建word导出模板 1、本地创建一个test.docx 2、将最终需要的文档内容及样式编辑完成(图1) 3、将所需动态值的位置,替换为变量参数(图2) 注: 动态值书写 图1 图2 模板值的书写要求 二、项目中使用 1、安装依赖 npm install docxtemplater-image-module-free --save n…...

AIGC | 如何用“Flow”,轻松解决复杂业务问题
随着LLM(大语言模型)的爆火,不少企业都在寻找通过LLM解决企业业务问题的方法,以达到降本增效的效果。但是,当面对较为复杂的业务问题(如:背景资料多、问题分类多、条件判断复杂、涉及模块多等&a…...

多级菜单 树结构 排序 前端 后端 java
目录 省流: 正文: v1.0版 前端传的值: 后端代码: v2.0版 v3.0版 省流: 前端提交过来整个树即可。 给整个树进行sort。代码如下: public static void sort(List<Node> tree){int i 0;for…...
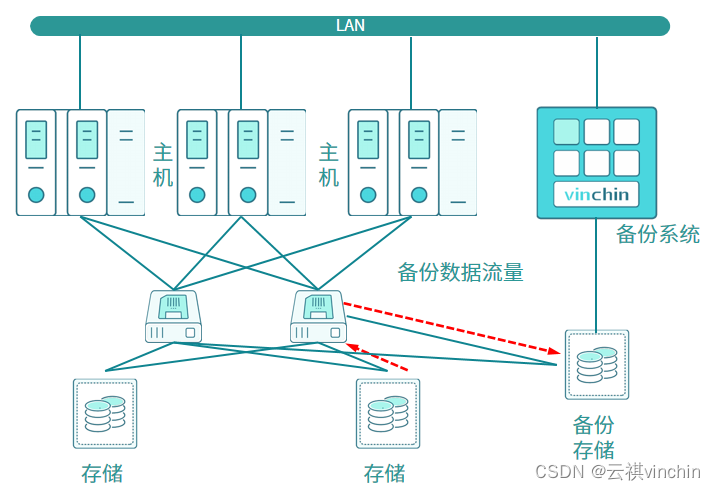
LAN-Free在数据备份时的应用与优势
在灾备领域中,常见的备份架构有LAN、LAN-Free和Server-Free备份,其中LAN备份架构图见图1,LAN-Free备份架构图见图2,Server-Free备份架构图见图3,途中红色箭头为备份数据流量走向: 图 1 图 2 图 3 从图1、图…...

HTML 文档声明和语言设置
HTML 文档声明 DOCTYPE 文档类型声明,用于告诉浏览器的解析器,该以那种 HTML 版本来解析这个文件。 HTML 5 版本声明 <!DOCTYPE html>XHTML 1.0 严格版声明 <!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Strict//EN" "http:/…...

【C++基础知识学习笔记】精华版(复习专用)
常用语法 函数重载(Overload) 规则: 函数名相同 参数个数不同、参数类型不同、参数顺序不同 注意: 返回值类型与函数重载无关 调用函数时,实参的隐式类型转换可能会产生二义性 默认参数 C++ 允许函数设置默认参数,在调用时可以根据情况省略实参。规则如下: 默认参数只能…...
探索ChatGPT在学术写作中的应用与心得
随着人工智能的迅猛发展,ChatGPT作为一种强大的自然语言处理模型,逐渐在学术界引起了广泛的关注。本文将探讨ChatGPT在学术写作中的应用,并分享使用ChatGPT进行学术写作时的一些经验和心得。 01 — ChatGPT在学术写作中的应用 1.文献综述和…...

Android:怎么学习才能更好的进大厂呢?
怎么学习才能更好的进大厂呢? 很多朋友都在问这个问题。 其实没有什么特别的技巧,就是依靠自己的毅力和决心。一天做不到,就一个月;一个月做不到,就一年。只要有决心,无论学历或资历如何,都不是…...

CSS标点符号换行问题
最近遇到一个奇怪的现象,元素中中文文本正常显示,但是加了一堆符号后中文文本居然换行了. div{width: 200px;border: 1px solid blue;word-break: break-all;} <div>文本</div>经过研究发现,因为标点符号不允许出现在行首和行尾,连带着符号…...
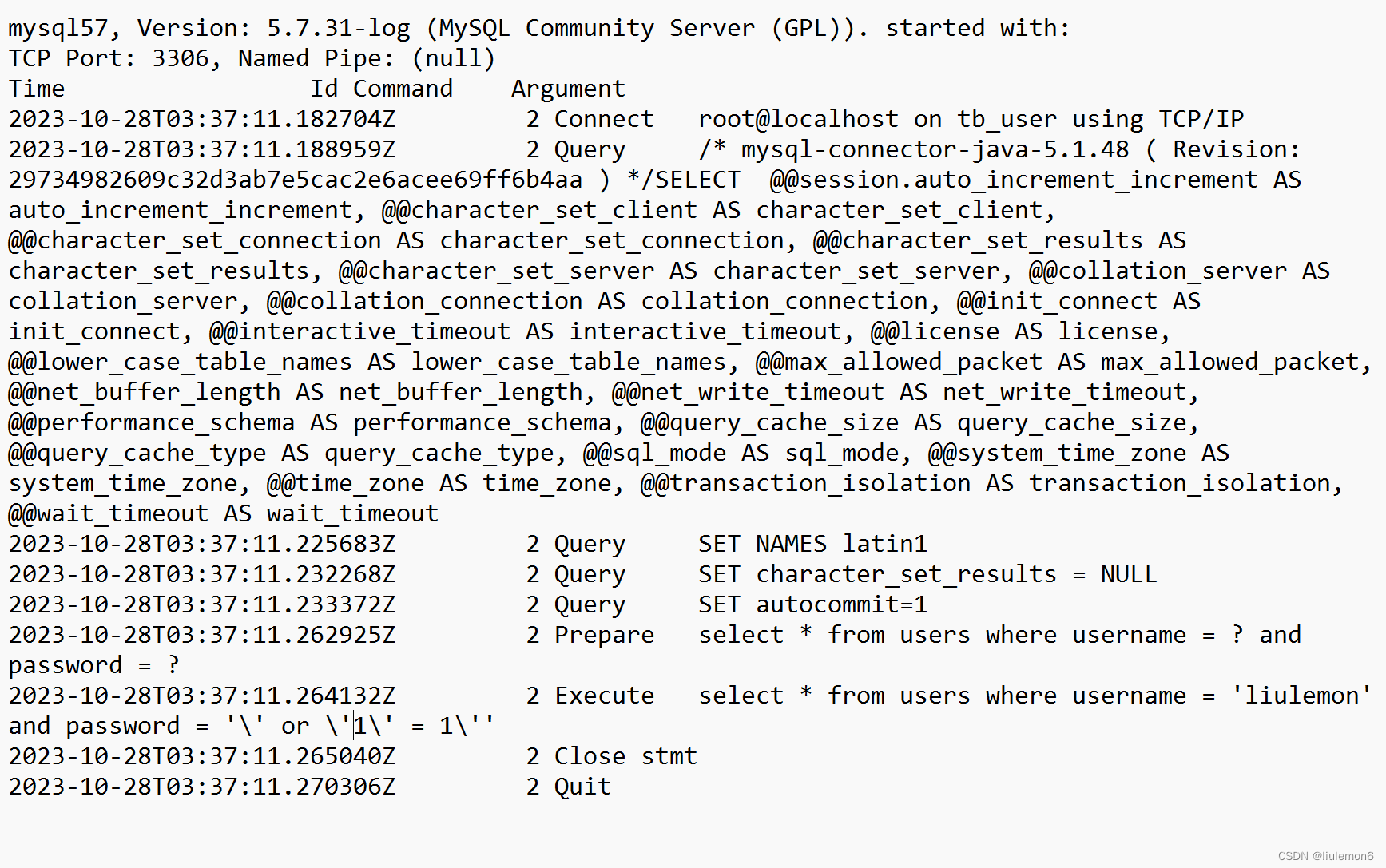
jdbc Preparestatement防止SQL注入的原理
2023-10-28T03:37:11.264132Z 2 Execute select * from users where username liulemon and password \ or \1\ 1\ 可以看到这一行,预编译时?变成了转义字符 useServerPrepStmtstrue加上这句才能预编译...

如何控制 LLM 的输出格式和解析其输出结果?
现在很多人对于如何使用像 ChatGPT 这样的 LLM 已经比较有经验了,可以使用各种不同的 Prompt 得到自己想要的结果。但有时候我们的使用场景不局限于手动操作,而是需要结合程序去调用 API,并且解析 API 的返回结果,从而实现一些自动…...

【Linux】 ps 命令使用
ps (英文全拼:process status)命令用于显示当前进程的状态,类似于 windows 的任务管理器。 语法 ps [选项] ps命令 -Linux手册页 著者 ps最初由布兰科兰克斯特撰写<lankestefwi.uva.nl>。迈克尔K约翰逊<johnsonmred…...

C++二分查找算法的应用:长度递增组的最大数目
本文涉及的基础知识点 二分查找 题目 给你一个下标从 0 开始、长度为 n 的数组 usageLimits 。 你的任务是使用从 0 到 n - 1 的数字创建若干组,并确保每个数字 i 在 所有组 中使用的次数总共不超过 usageLimits[i] 次。此外,还必须满足以下条件&…...

提示3D标题编辑器仍在运行怎么解决,以及3D标题编辑器怎么使用
在进行视频剪辑时,尤其是剪辑一些带有文字的开场视频,一般都会使用具有立体效果的3D标题,这样制作出来的视频效果不仅好看,还非常的炫酷,但是对于一些刚刚开始接触视频剪辑的小伙伴来说,可能对3D标题还不是…...
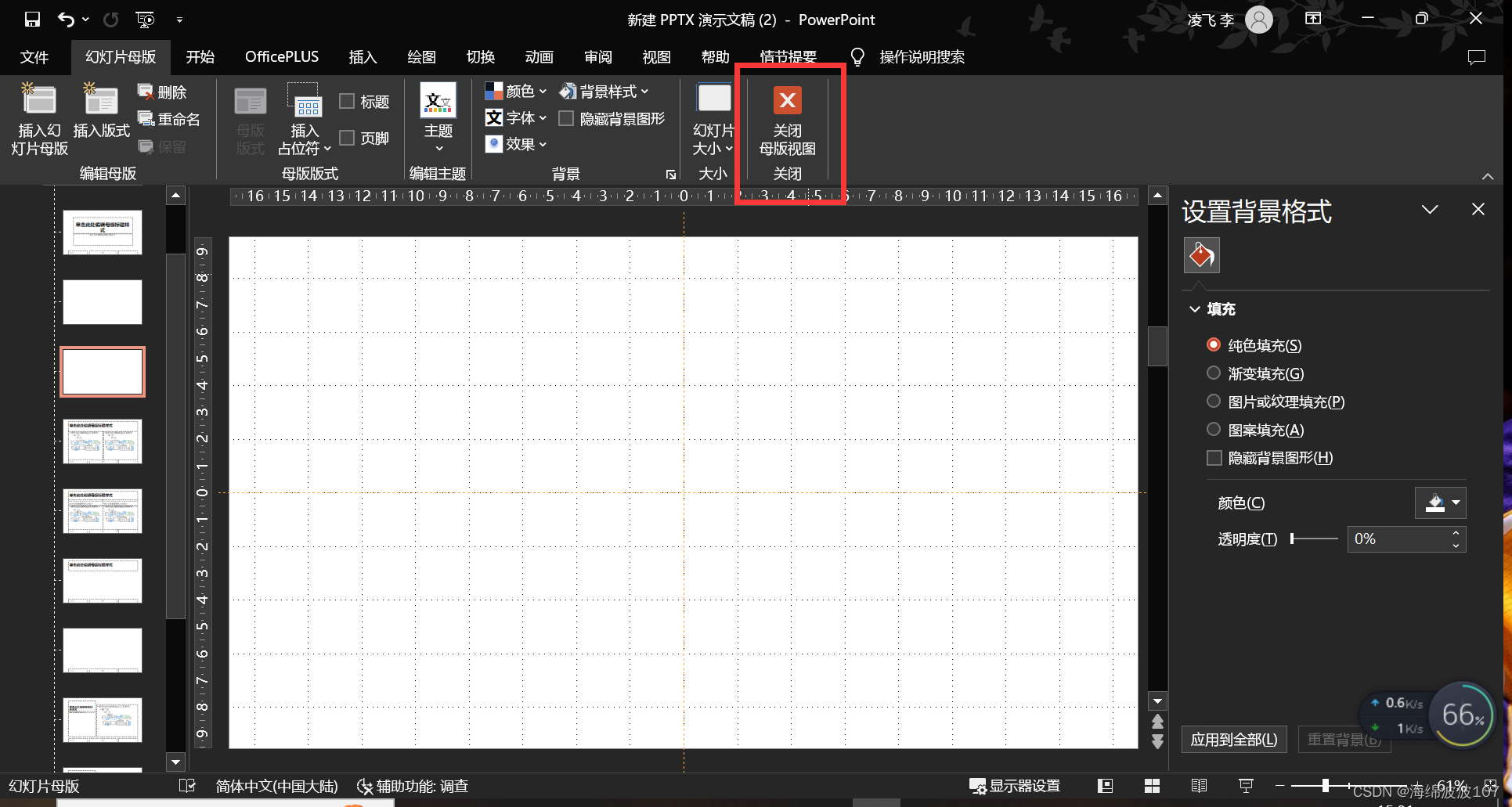
1. PPT高效初始化设置
1. PPT高效初始化设置 软件安装:Office 2019 主题和颜色 颜色可以在白天与黑夜切换,护眼 切换成了黑色 撤回次数 撤回次数太少,只有20次怎么办 自动保存 有时忘记保存就突然关闭,很需要一个自动保存功能 图片压缩 图…...

el-cascader级联选择器选中一个全选中问题
问题 只选中一个却把同级全选中 解决 :props中添加label、value、children属性 label、value、children属性值需要和后端返回的集合中的字段名保持一致 后端返回数据:...

Opencascad(C++)-创建自定义坐标系
文章目录 1、前言2、在Opencascad中显示小的坐标系3、在Opencascad中创建自定义的坐标系 1、前言 在Opencascad开发时,在view中可以显示小的坐标系,但是有时我们需要在建模时创建基准坐标系,当然可以作为工件坐标系也可以作为基准坐标系。本…...
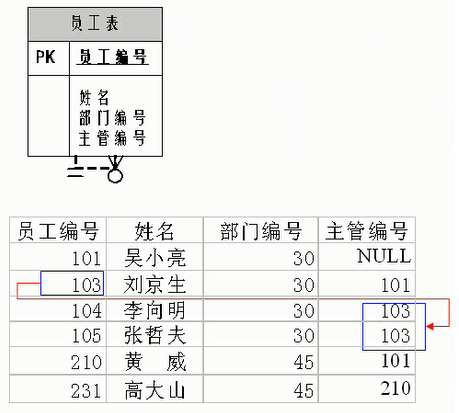
MySQL数据库入门到大牛_01_数据库概述
文章目录 1. 为什么要使用数据库2. 数据库与数据库管理系统2.1 数据库的相关概念2.2 数据库与数据库管理系统的关系2.3 常见的数据库管理系统排名(DBMS)2.4 常见的数据库介绍 3. MySQL介绍3.1 概述3.2 MySQL发展史重大事件3.3 关于MySQL 8.03.4 Why choose MySQL?3.5 Oracle v…...
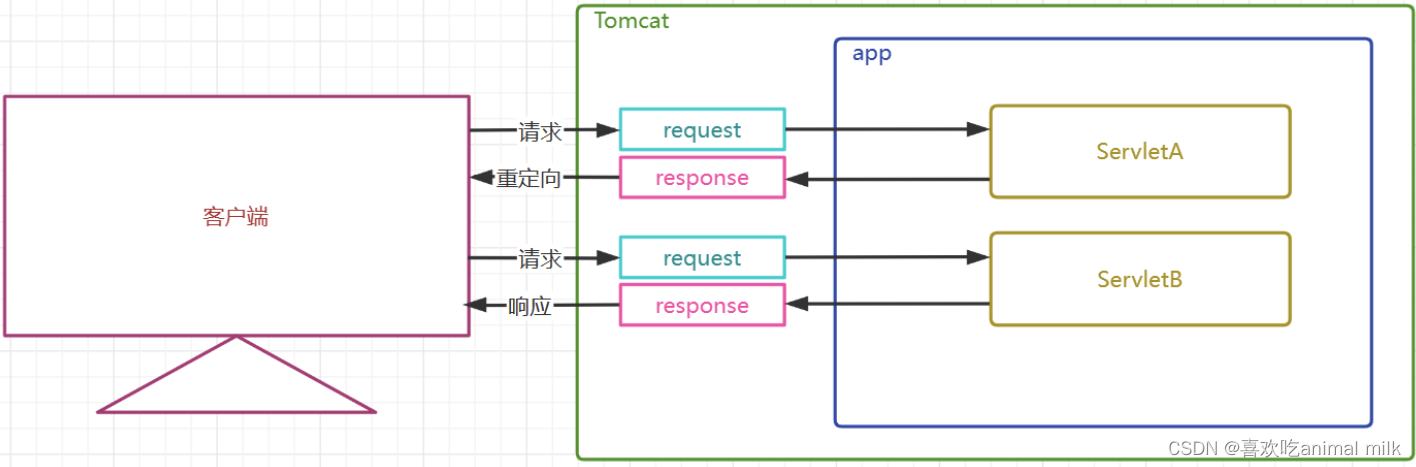
Web - Servlet详解
目录 前言 一 . Servlet简介 1.1 动态资源和静态资源 1.2 Servlet简介 二 . Servlet开发流程 2.1 目标 2.2 开发过程 三 . Servlet注解方式配置 编辑 四 . servlet生命周期 4.1 生命周期简介 4.2 生命周期测试 4.3 生命周期总结 五 . servlet继承结构 5.1 ser…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...

Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析
Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析 一、第一轮基础概念问题 1. Spring框架的核心容器是什么?它的作用是什么? Spring框架的核心容器是IoC(控制反转)容器。它的主要作用是管理对…...
0609)
书籍“之“字形打印矩阵(8)0609
题目 给定一个矩阵matrix,按照"之"字形的方式打印这个矩阵,例如: 1 2 3 4 5 6 7 8 9 10 11 12 ”之“字形打印的结果为:1,…...

PostgreSQL 与 SQL 基础:为 Fast API 打下数据基础
在构建任何动态、数据驱动的Web API时,一个稳定高效的数据存储方案是不可或缺的。对于使用Python FastAPI的开发者来说,深入理解关系型数据库的工作原理、掌握SQL这门与数据库“对话”的语言,以及学会如何在Python中操作数据库,是…...
