【学习笔记】[PA2019] Osady i warownie 2
这题好抽象😱
EI 说这题可以转化为对偶图,但是我完全没看懂😅
考虑维护最向右和向下的两条路径,那么不能放的位置就是两条路径的交(感性理解一下)
考虑抽象的描述这条路径, r i r_i ri表示第 i i i行能到达的最大的列,那么 { r i } \{r_i\} {ri}是单调不降的,等价于我们要维护字典序最大/最小的路径
考虑向下的怎么维护。首先,这个点一定要在路径上,即 r x − 1 ≤ y ≤ r x r_{x-1}\le y\le r_x rx−1≤y≤rx(假设插入的点是 ( x , y ) (x,y) (x,y));其次,我们希望以最小的代价调整(尽量保持前缀不变),但是又必须绕过 ( x , y ) (x,y) (x,y),这等价于 ∀ i ≥ x − 1 , r i = max ( r i , y + 1 ) \forall i\ge x-1,r_i=\max(r_i,y+1) ∀i≥x−1,ri=max(ri,y+1)。注意到每次调整时至少有一个障碍以后不会被考虑到,因此总调整数目不会超过 O ( k ) O(k) O(k)。
因此递归下去即可。
复杂度 O ( k log k ) O(k\log k) O(klogk)。
#include<bits/stdc++.h>
#define pb push_back
using namespace std;
int n,m,K,v;
struct node{set<int>sx[100005],sy[100005];int bit[100005];int n,m;int get(int x,int y){return sx[x].count(y);}void add(int x,int y){for(x++;x<=n;x+=x&-x)bit[x]=max(bit[x],y);}int qmax(int x){int y(0);for(x++;x;x-=x&-x)y=max(y,bit[x]);return y;}int query(int x,int y){if(x==0)return qmax(x)>=y;return qmax(x-1)<=y&&y<=qmax(x);}void upd(int x,int y){if(!query(x,y))return;add(x-1,y+1),x--,y++;if(sx[x].size()&&sx[x].upper_bound(y)!=sx[x].begin()){auto it=--sx[x].upper_bound(y);upd(x,*it);}if(sy[y].size()&&sy[y].lower_bound(x)!=sy[y].end()){auto it=sy[y].lower_bound(x);upd(*it,y);}}void ins(int x,int y){sx[x].insert(y),sy[y].insert(x);upd(x,y);}
}R,D;
int main(){ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);cin>>n>>m>>K;D.n=n,D.m=m;R.n=m,R.m=n;D.add(n-1,m-1);R.add(m-1,n-1);for(int i=1;i<=K;i++){int r,c,z;cin>>r>>c>>z;r=(r^v)%n,c=(c^v)%m;if(D.get(r,c)){cout<<"NIE"<<"\n";}else if(D.query(r,c)&&R.query(c,r)){cout<<"TAK"<<"\n";v^=z;} else{cout<<"NIE"<<"\n";D.ins(r,c),R.ins(c,r);}}
}
相关文章:

【学习笔记】[PA2019] Osady i warownie 2
这题好抽象😱 EI 说这题可以转化为对偶图,但是我完全没看懂😅 考虑维护最向右和向下的两条路径,那么不能放的位置就是两条路径的交(感性理解一下) 考虑抽象的描述这条路径, r i r_i ri表示…...

Flask——接口路由技术
接口路由技术 一、Flask 简介1、环境安装:2、一个最小的应用3、两种运行方式 二、定义路由1、普通路由2、动态路由3、限定类型4、地址尾部的“/” 三、请求与响应-请求方法四、请求与响应-处理请求数据1、request的常用属性/方法2、get 请求参数3、json 请求4、表单…...

Dubbo篇---第一篇
系列文章目录 文章目录 系列文章目录一、说说一次 Dubbo 服务请求流程?二、说说 Dubbo 工作原理三、Dubbo 支持哪些协议?一、说说一次 Dubbo 服务请求流程? 基本工作流程: 上图中角色说明: 二、说说 Dubbo 工作原理 工作原理分 10 层: 第一层:service 层,接口层,…...

powermock-成员变量赋值
powermock成员变量设置 //被测试类 Service public class Demo {private String aaa ;public String method1(){return aaa;} }//测试类,测试类中使用了mockito、和powermock,用powermock设置成员变量相较于mockito简洁一些,一般mockito和po…...

Axios请求成功和失败时分别执行哪个函数?
在 Axios 中,请求成功和失败时分别执行的函数是 then 和 catch。 特点: then 函数用于处理请求成功的情况,它接受一个回调函数作为参数,在请求成功时会调用该回调函数。catch 函数用于处理请求失败的情况,它也接受一…...

【Linux】进程概念III --fork函数解析
Halo,这里是Ppeua。平时主要更新C语言,C,数据结构算法…感兴趣就关注我吧!你定不会失望。 本篇导航 0. 创建进程1. 认识fork函数2.使用Fork函数3.关于fork的为什么3.1 一个函数如何返回两次?fork究竟在干什么?3.2 为什么要给子…...
)
关闭 Android SplashScreen(闪屏)
SplashScreen在Android 12上是强制的,如果你什么都不做,你的App在Android 12上就会自动拥有SplashScreen界面 但是这个SplashScreen界面太局限了能改的地方太少了 其实也没什么他主要作用是为了在App启动初始化的时候避免让用户在一个空白界面等待过长时…...

react_16
主页 import {DownCircleOutlined,MenuFoldOutlined,VerticalAlignTopOutlined, } from "ant-design/icons"; import { Button, Layout, Menu } from "antd"; import { ItemType } from "antd/es/menu/hooks/useItems"; import { Link, Navigat…...
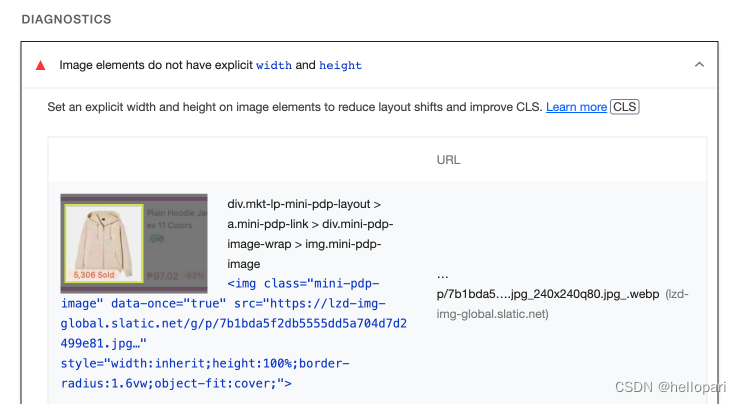
前端性能分析工具
前段时间在工作中,需要判断模块bundle size缩减对页面的哪些性能产生了影响, 因此需要了解前端的性能指标如何定义的,以及前端有哪些性能分析工具, 于是顺便整理了一篇笔记, 以供前端小白对性能这块知识点做一个入门级的了解. 页面渲染 在了解性能指标和分析工具之前,有必要先…...

根据Aurora发送时序,造Aurora 数据包,从而进行AXIS接口数据位宽转换仿真
首先Aurora采用AXIS接口 由于后续需要进行AXIS接口 不同时钟域的数据位宽转换(64bit和256bit之间的转换),因此分两次走。 第一种方法:采用AXIS数据位宽转换IP AXIS跨时钟域IP 第二种方法:逻辑完成 下面记录逻辑…...

java后端响应结果Result
目录 一、Result1-1、响应代码1-2、调用响应1-3、在前端vue页面使用方法 一、Result 1-1、响应代码 package com.aaa.common;import lombok.AllArgsConstructor; import lombok.Data; import lombok.NoArgsConstructor;Data AllArgsConstructor NoArgsConstructor public cla…...

react_11
MobX 介绍 需求,组件0 改变了数据,其它组件也想获得改变后的数据,如图所示 这种多个组件之间要共享状态数据,useState 就不够用了,useContext 也不好用了 能够和 react 配合使用的状态管理库有 MobX Redux 其中…...

AI:52-基于深度学习的垃圾分类
🚀 本文选自专栏:AI领域专栏 从基础到实践,深入了解算法、案例和最新趋势。无论你是初学者还是经验丰富的数据科学家,通过案例和项目实践,掌握核心概念和实用技能。每篇案例都包含代码实例,详细讲解供大家学习。 📌📌📌本专栏包含以下学习方向: 机器学习、深度学…...

[shell,hive] 在shell脚本中将hiveSQL分离出去
将Hive SQL语句写在单独的.hql文件中, 然后在shell脚本中调用这些文件来执行Hive查询。 这样可以将SQL语句与shell脚本分离,使代码更加清晰和易于维护。 基本用法 以下是一个示例,展示如何在shell脚本中使用.hql文件执行Hive查询…...
向量之间的rpy夹角)
求两个(法)向量之间的rpy夹角
主要使用Eigen库实现: 1. 四元素到欧拉角的转换 #include <array> #include <Eigen/Geometry>template <typename T> inline Eigen::Matrix<typename std::remove_reference<T>::type::Scalar, 3, 1> eulerAnglesZYX(T q_in) {typedef typenam…...
)
[100天算法】-每个元音包含偶数次的最长子字符串(day 53)
题目描述 给你一个字符串 s ,请你返回满足以下条件的最长子字符串的长度:每个元音字母,即 a,e,i,o,u ,在子字符串中都恰好出现了偶数次。示例 1:输入:s &qu…...
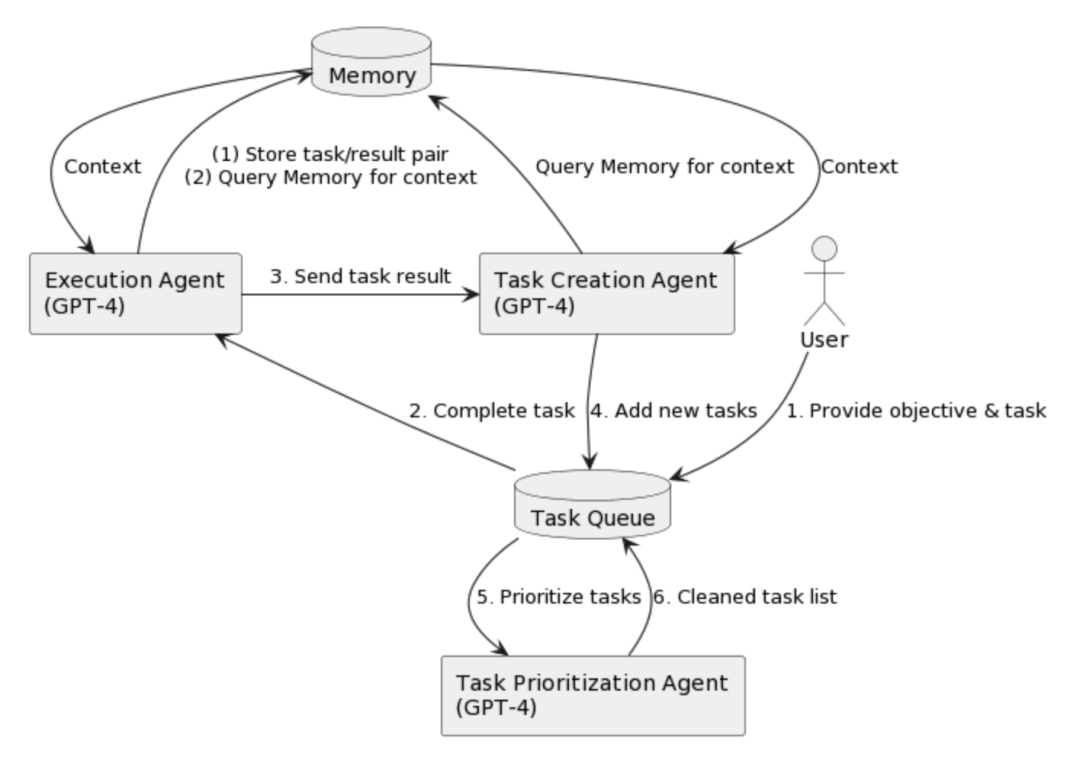
从科幻走向现实,LLM Agent 做到哪一步了?
LLM 洪流滚滚,AI 浪潮席卷全球,在这不断冲击行业认知的一年中,Agent 以冉冉新星之态引起开发者侧目。OpenAI 科学家 Andrej Karpathy 曾言“OpenAI 在大模型领域快人一步,但在 Agent 领域,却是和大家处在同一起跑线上。…...

[笔记] 数据类型
整形 一字节(Byte,也就是平时KB、MB里面的B)就是八个二进制位(bit) 整形——int——4B无符号整形——unsigned int——4B短整形——short——2B长整型——long——4B双长整型——long long——8B 浮点型 参考博客:C 语言的浮点类型…...
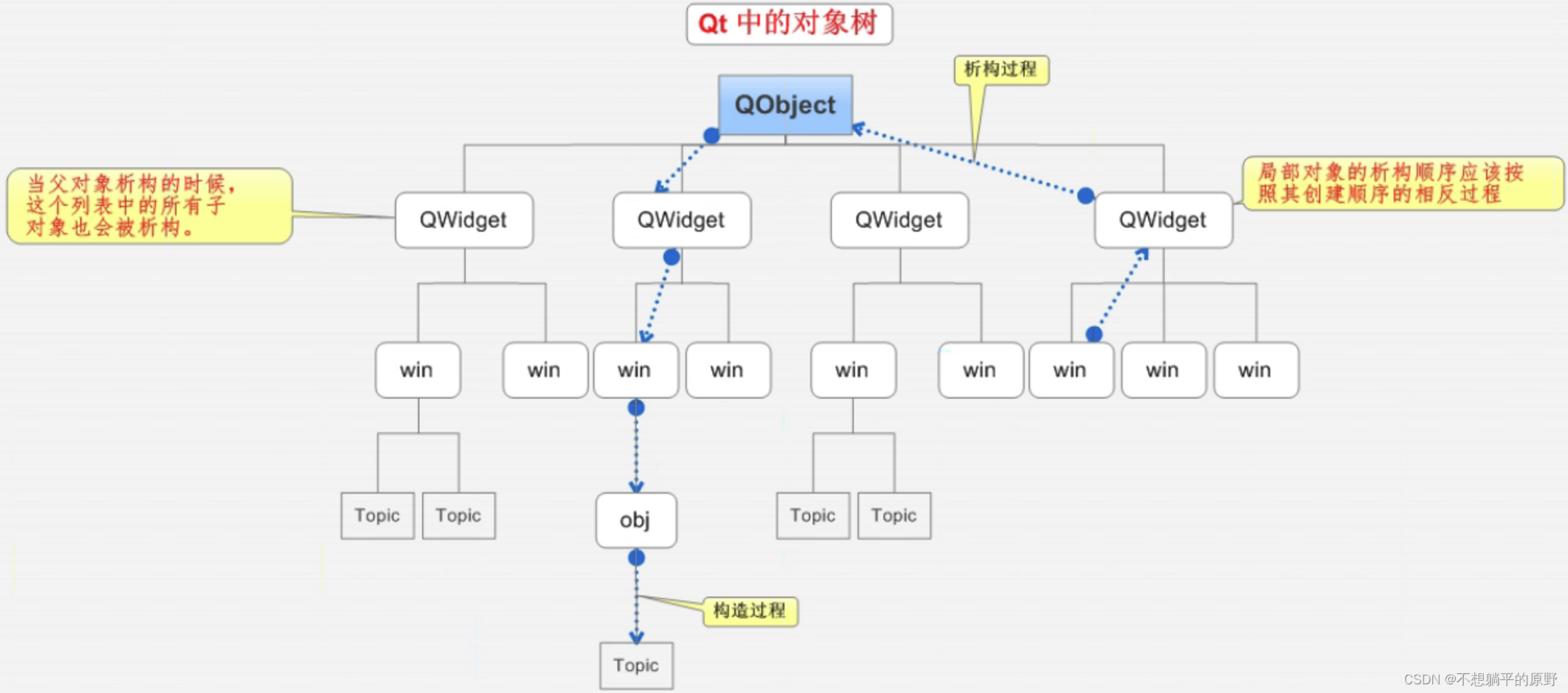
QT学习之QT概述
1.1 什么是QT? Qt是一个跨平台的C图形用户界面应用程序框架。 QT特点: 跨平台,几乎支持所有的平台接口简单,容易上手,学习QT框架对学习其他框架有参考意义。一定程度上简化了内存回收机制开发效率高,能够…...
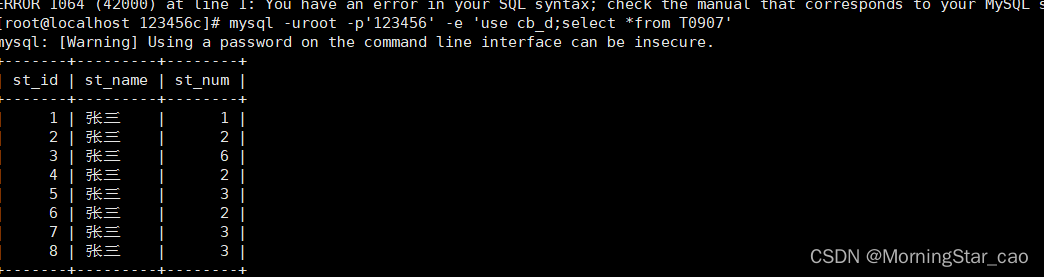
编写shell脚本,利用mysqldump实现MySQL数据库分库分表备份
查看数据和数据表 mysql -uroot -p123456 -e show databases mysql -uroot -p123456 -e show tables from cb_d 删除头部Database和数据库自带的表 mysql -uroot -p123456 -e show databases -N | egrep -v "information_schema|mysql|performance_schema|sys"编写…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...

6.9-QT模拟计算器
源码: 头文件: widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QMouseEvent>QT_BEGIN_NAMESPACE namespace Ui { class Widget; } QT_END_NAMESPACEclass Widget : public QWidget {Q_OBJECTpublic:Widget(QWidget *parent nullptr);…...
