【MATLAB】全网唯一的13种信号分解+FFT傅里叶频谱变换联合算法全家桶
有意向获取代码,请转文末观看代码获取方式~
大家吃一顿火锅的价格便可以拥有13种信号分解+FFT傅里叶频谱变换联合算法,绝对不亏,知识付费是现今时代的趋势,而且都是我精心制作的教程,有问题可随时反馈~也可单独获取某一算法的代码(见每一算法介绍后文)~
1 【MATLAB】EMD 信号分解+FFT傅里叶频谱变换联合算法
EMD 是一种信号分解方法,它将一个信号分解成有限个本质模态函数 (EMD) 的和,每个 EMD 都是具有局部特征的振动模式。EMD 分解的主要步骤如下:
-
将信号的局部极大值和极小值连接起来,形成一些局部极值包络线。
-
对于每个局部极值包络线,通过线性插值得到一条平滑的包络线。然后将原信号减去该包络线,得到一条局部振荡的残差信号。
-
对于该残差信号,重复步骤1和2,直到无法再分解出新的局部振荡模式为止。
-
将所有的局部振荡模式相加,得到原始信号的EMD分解。 EMD分解的优点是能够很好地处理非线性和非平稳信号,并且不需要预先设定基函数。因此,EMD分解在信号处理、图像处理和模式识别等领域得到了广泛的应用。
原始数据分解各分量示意图

傅里叶变换是一种数学方法,用于将一个信号分解成一系列正弦和余弦函数的和,从而更好地理解和处理信号。傅里叶变换在信号处理领域有着广泛的应用,包括音频处理、图像处理等。 具体来说,傅里叶变换的步骤如下:
-
给定一个连续时间域函数f(t),其中t为时间。
-
对f(t)进行傅里叶变换,得到它的频率域表示F(ω),其中ω为角频率。
-
F(ω)表示了f(t)中所有频率分量的幅度和相位信息。
-
将F(ω)分解成一系列正弦和余弦函数的和,即: F(ω) = ∑[a(k)cos(kω) + b(k)sin(kω)] 其中,k为频率分量的序号,a(k)和b(k)分别为对应的正弦和余弦函数的系数。 傅里叶变换的优点是可以将时间域中的信号转换成频率域中的信号,从而更好地理解信号的频率分量和周期性特征,同时也方便进行一些信号处理任务,例如滤波、降噪等。缺点是傅里叶变换需要对整个信号进行处理,计算量较大,在实时处理等场景下可能会存在较大的延迟。

2【MATLAB】EEMD信号分解+FFT傅里叶频谱变换联合算法
EEMD是对EMD的改进,可以克服EMD的一些缺点。EEMD的主要思想是通过对原始数据集进行多次噪声扰动,获得多个EMD分解的集合,然后将这些EMD集合求平均,得到最终的EEMD分解结果。EEMD的主要步骤如下:
-
对原始信号进行若干次随机噪声扰动,得到多个噪声扰动数据集。
-
对每个噪声扰动数据集进行EMD分解,得到多个EMD分解集合。
-
将每个 EMD 分解集合的对应分量进行平均,得到最终的 EEMD 分解结果。 EEMD 分解的优点是能够克服 EMD 的局限性,如基函数的选择和模态重叠等问题。同时,EEMD 还可以提供更好的信噪比和更高的分解精度。因此,EEMD 在信号处理、图像处理和模式识别等领域也得到了广泛的应用。
原始数据分解各分量示意图

原始数据分解各分量的箱型图
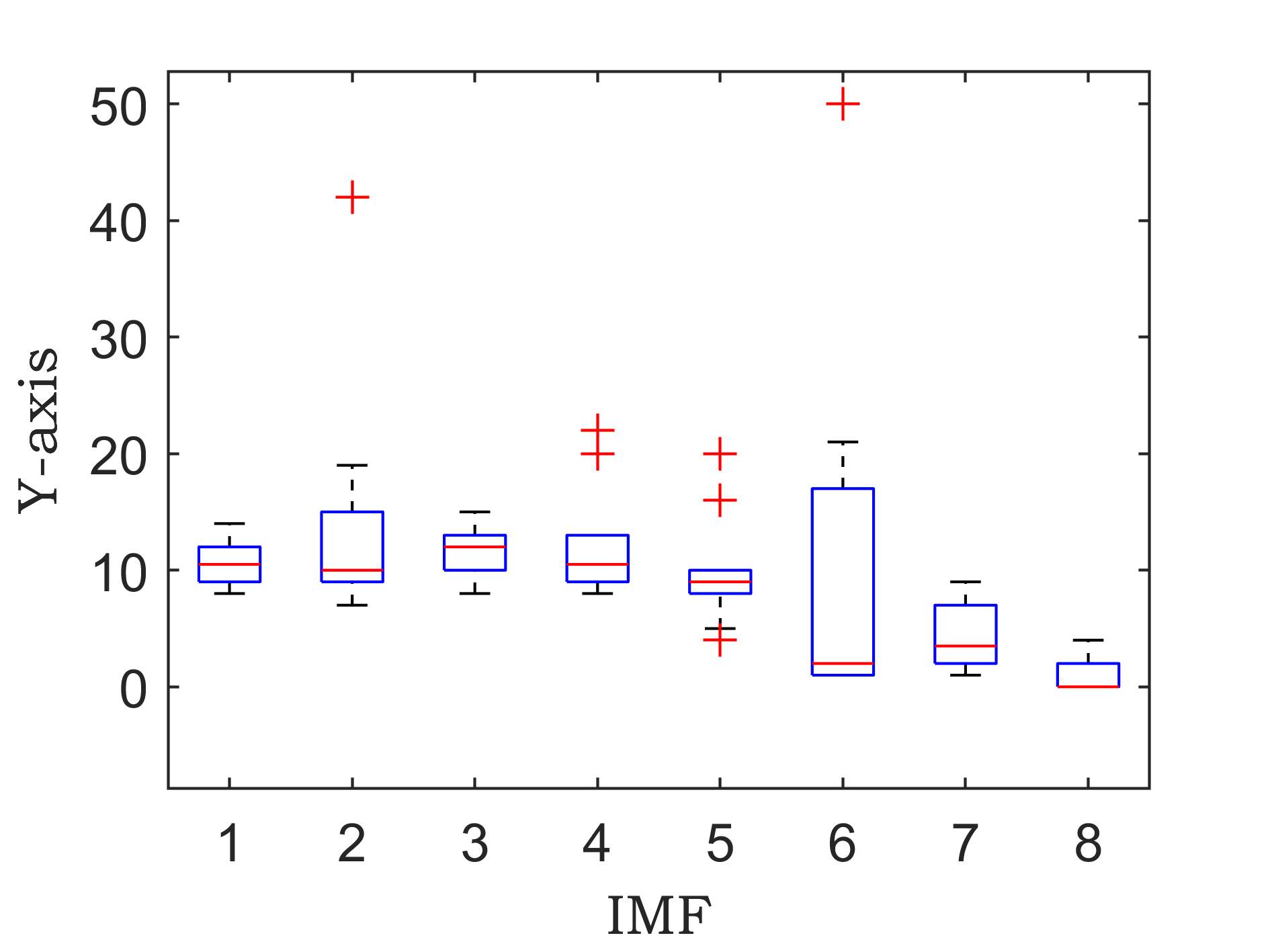
傅里叶变换是一种数学方法,用于将一个信号分解成一系列正弦和余弦函数的和,从而更好地理解和处理信号。傅里叶变换在信号处理领域有着广泛的应用,包括音频处理、图像处理等。 具体来说,傅里叶变换的步骤如下:
-
给定一个连续时间域函数f(t),其中t为时间。
-
对f(t)进行傅里叶变换,得到它的频率域表示F(ω),其中ω为角频率。
-
F(ω)表示了f(t)中所有频率分量的幅度和相位信息。
-
将F(ω)分解成一系列正弦和余弦函数的和,即: F(ω) = ∑[a(k)cos(kω) + b(k)sin(kω)] 其中,k为频率分量的序号,a(k)和b(k)分别为对应的正弦和余弦函数的系数。 傅里叶变换的优点是可以将时间域中的信号转换成频率域中的信号,从而更好地理解信号的频率分量和周期性特征,同时也方便进行一些信号处理任务,例如滤波、降噪等。缺点是傅里叶变换需要对整个信号进行处理,计算量较大,在实时处理等场景下可能会存在较大的延迟。
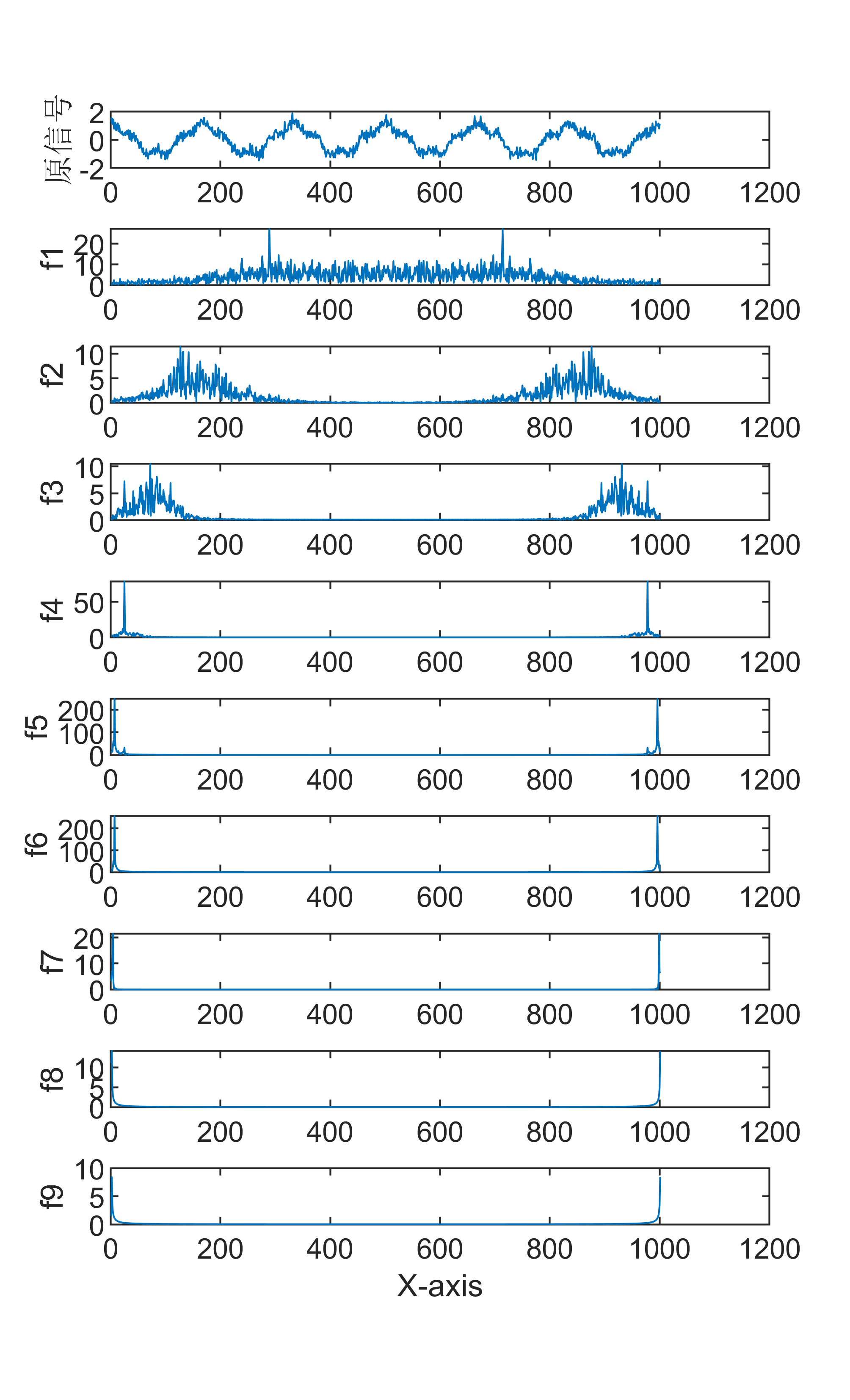
3【MATLAB】CEEMD信号分解+FFT傅里叶频谱变换联合算法
CEEMD是对EEMD的改进,它在EEMD的基础上引入了一个自适应的扩展方法,可以更好地解决EMD/EEMD中存在的模态混叠问题。CEEMD的主要步骤如下:
-
对原始信号进行若干次随机噪声扰动,得到多个噪声扰动数据集。
-
对每个噪声扰动数据集进行EMD分解,得到多个EMD分解集合。
-
对于每个EMD分解集合,通过一个自适应的扩展方法,将每个局部模态函数分配到它所属的固有模态函数上,消除模态混叠的影响。
-
将每个扩展后的 EMD 分解集合的对应分量进行平均,得到最终的 CEEMD 分解结果。 CEEMD 分解具有良好的局部性和自适应性,能够更准确地分解信号,同时避免了 EEMD 中的模态混叠问题。因此,CEEMD 在信号处理、图像处理和模式识别等领域也得到了广泛的应用。
原始数据分解各分量示意图
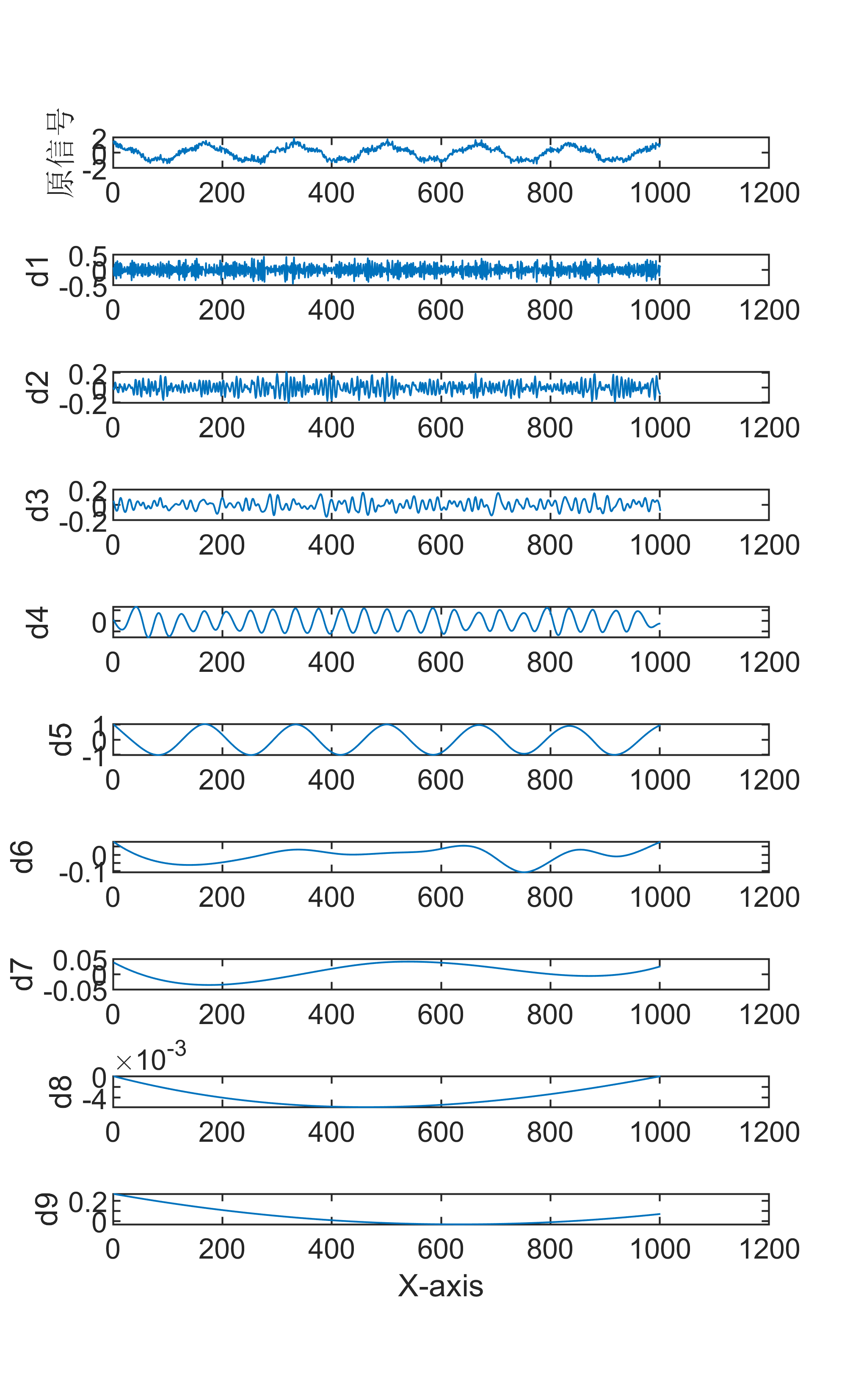
傅里叶变换是一种数学方法,用于将一个信号分解成一系列正弦和余弦函数的和,从而更好地理解和处理信号。傅里叶变换在信号处理领域有着广泛的应用,包括音频处理、图像处理等。 具体来说,傅里叶变换的步骤如下:
-
给定一个连续时间域函数f(t),其中t为时间。
-
对f(t)进行傅里叶变换,得到它的频率域表示F(ω),其中ω为角频率。
-
F(ω)表示了f(t)中所有频率分量的幅度和相位信息。
-
将F(ω)分解成一系列正弦和余弦函数的和,即: F(ω) = ∑[a(k)cos(kω) + b(k)sin(kω)] 其中,k为频率分量的序号,a(k)和b(k)分别为对应的正弦和余弦函数的系数。 傅里叶变换的优点是可以将时间域中的信号转换成频率域中的信号,从而更好地理解信号的频率分量和周期性特征,同时也方便进行一些信号处理任务,例如滤波、降噪等。缺点是傅里叶变换需要对整个信号进行处理,计算量较大,在实时处理等场景下可能会存在较大的延迟。
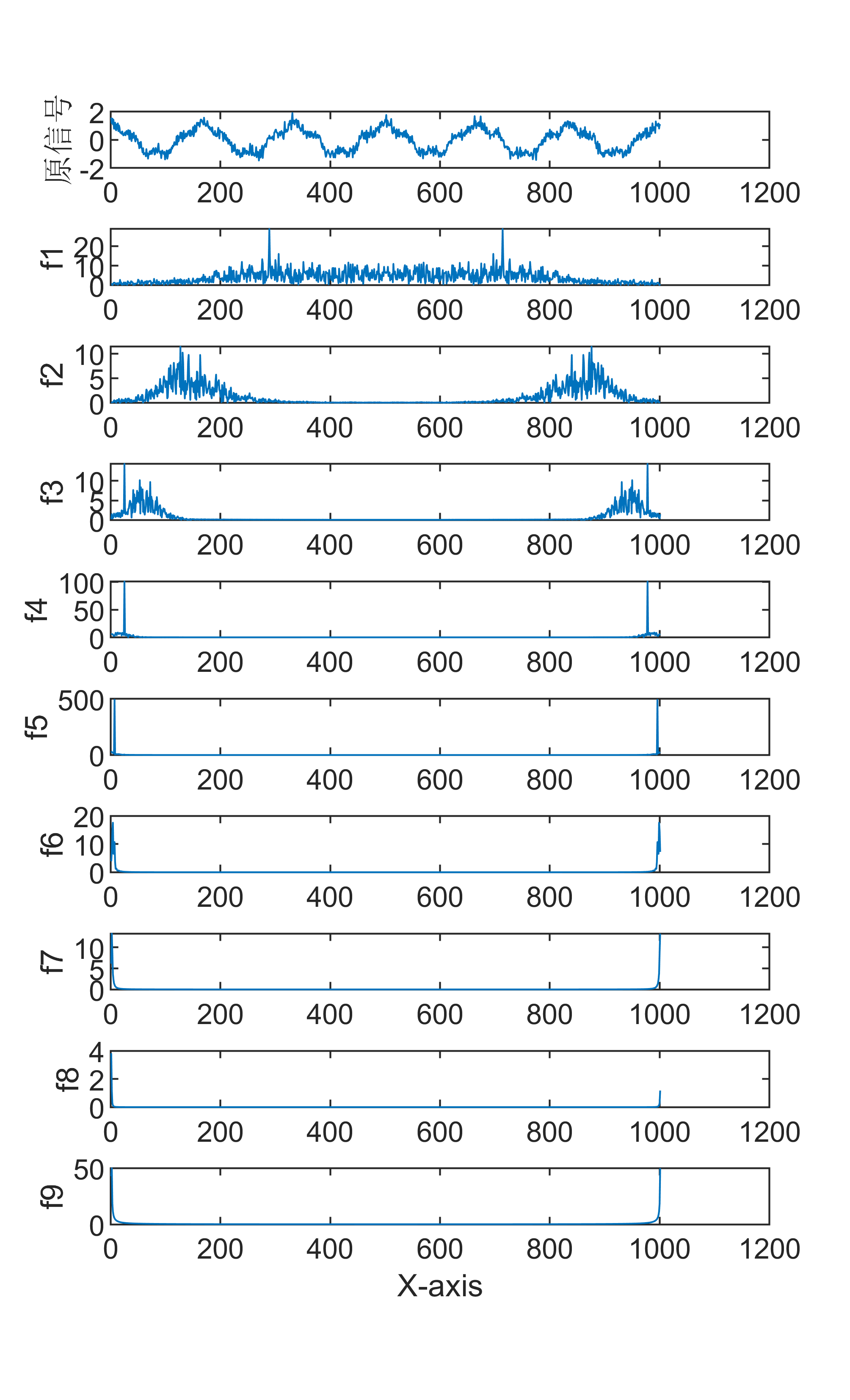
4【MATLAB】CEEMDAN信号分解+FFT傅里叶频谱变换联合算法
CEEMDAN是对CEEMD的进一步改进,它引入了一种自适应噪声辅助方法,可以更好地处理信号中的高频噪声。CEEMDAN的主要步骤如下:
-
对原始信号进行若干次随机噪声扰动,得到多个噪声扰动数据集。
-
对每个噪声扰动数据集进行CEEMD分解,得到多个CEEMD分解集合。
-
对于每个CEEMD分解集合,引入自适应噪声辅助方法,通过将噪声信号添加到每个局部模态函数中,增强信号的边缘和高频部分。
-
将每个自适应噪声辅助后的 CEEMD 分解集合的对应分量进行平均,得到最终的 CEEMDAN 分解结果。 CEEMDAN 分解具有更好的对高频噪声的适应性,能够更准确地分解信号。因此,CEEMDAN 在信号处理、图像处理和模式识别等领域也得到了广泛的应用。
原始数据分解各分量示意图

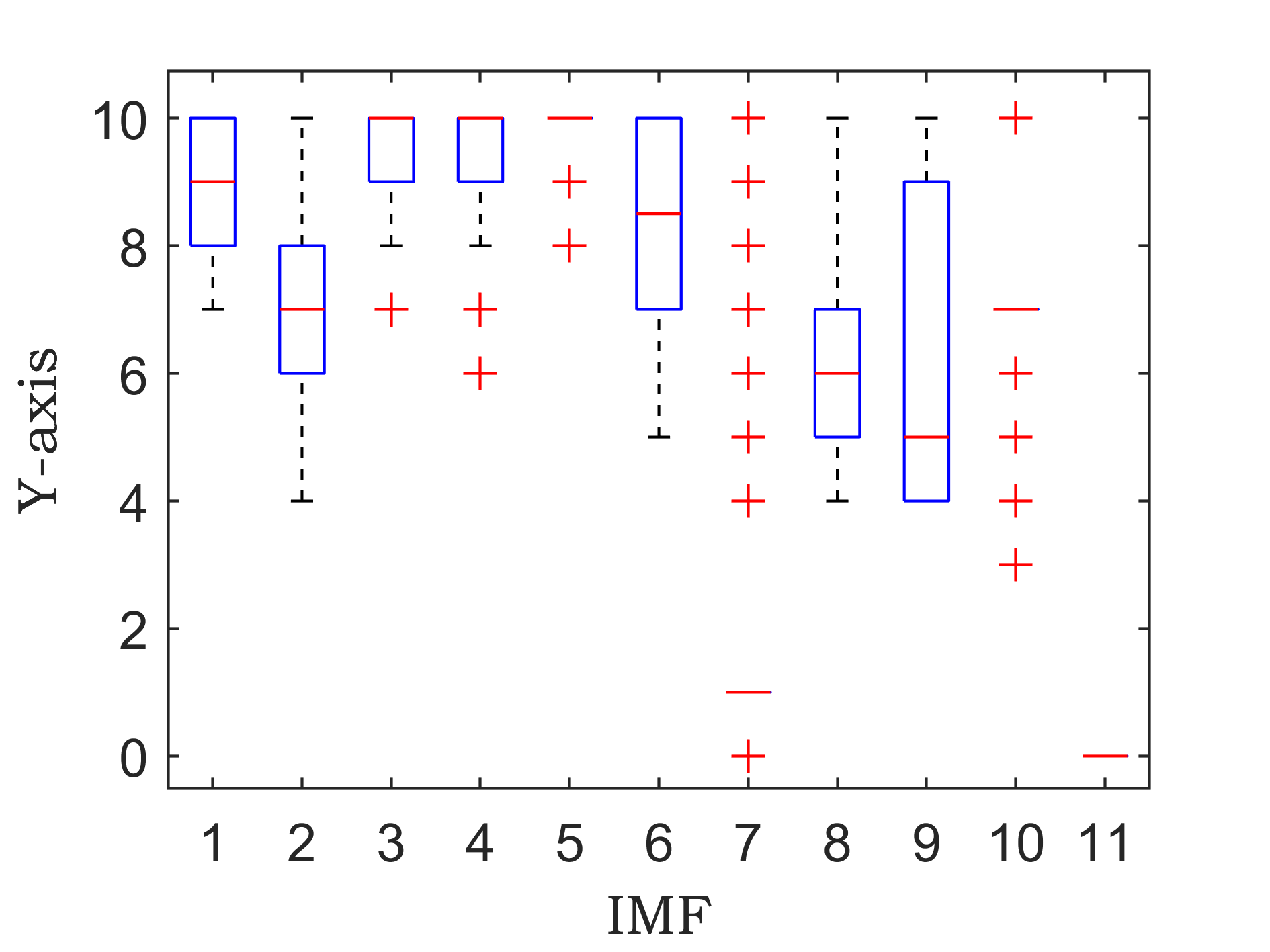
原始数据分解各分量的箱型图
傅里叶变换是一种数学方法,用于将一个信号分解成一系列正弦和余弦函数的和,从而更好地理解和处理信号。傅里叶变换在信号处理领域有着广泛的应用,包括音频处理、图像处理等。 具体来说,傅里叶变换的步骤如下:
-
给定一个连续时间域函数f(t),其中t为时间。
-
对f(t)进行傅里叶变换,得到它的频率域表示F(ω),其中ω为角频率。
-
F(ω)表示了f(t)中所有频率分量的幅度和相位信息。
-
将F(ω)分解成一系列正弦和余弦函数的和,即: F(ω) = ∑[a(k)cos(kω) + b(k)sin(kω)] 其中,k为频率分量的序号,a(k)和b(k)分别为对应的正弦和余弦函数的系数。 傅里叶变换的优点是可以将时间域中的信号转换成频率域中的信号,从而更好地理解信号的频率分量和周期性特征,同时也方便进行一些信号处理任务,例如滤波、降噪等。缺点是傅里叶变换需要对整个信号进行处理,计算量较大,在实时处理等场景下可能会存在较大的延迟。
5【MATLAB】ICEEMDAN信号分解+FFT傅里叶频谱变换联合算法
ICEEMDAN (Improved Complete Ensemble EMD with Adaptive Noise) 是一种基于经验模态分解(Empirical Mode Decomposition, EMD)的信号分解方法。与传统的 EMD 方法不同,ICEEMDAN 引入了自适应噪声和完整集成策略,以提高分解的稳定性和准确性。在 ICEEMDAN 方法中,首先采用 EMD 将原始信号分解成多个固有模态函数(Intrinsic Mode Functions, IMF),然后通过自适应噪声算法去除每个 IMF 中的噪声,最后将去噪后的 IMFs 进行完整集成,得到分解后的信号。相比于传统的 EMD 方法,ICEEMDAN 采用自适应噪声算法去除噪声,可以减少分解过程中的模态混叠问题。此外,完整集成策略可以保证分解后的信号保留了原始信号的全部信息,提高了分解的准确性。 ICEEMDAN 分解方法在信号处理、图像处理、语音处理等领域得到了广泛应用,具有较高的分解效果和可靠性。
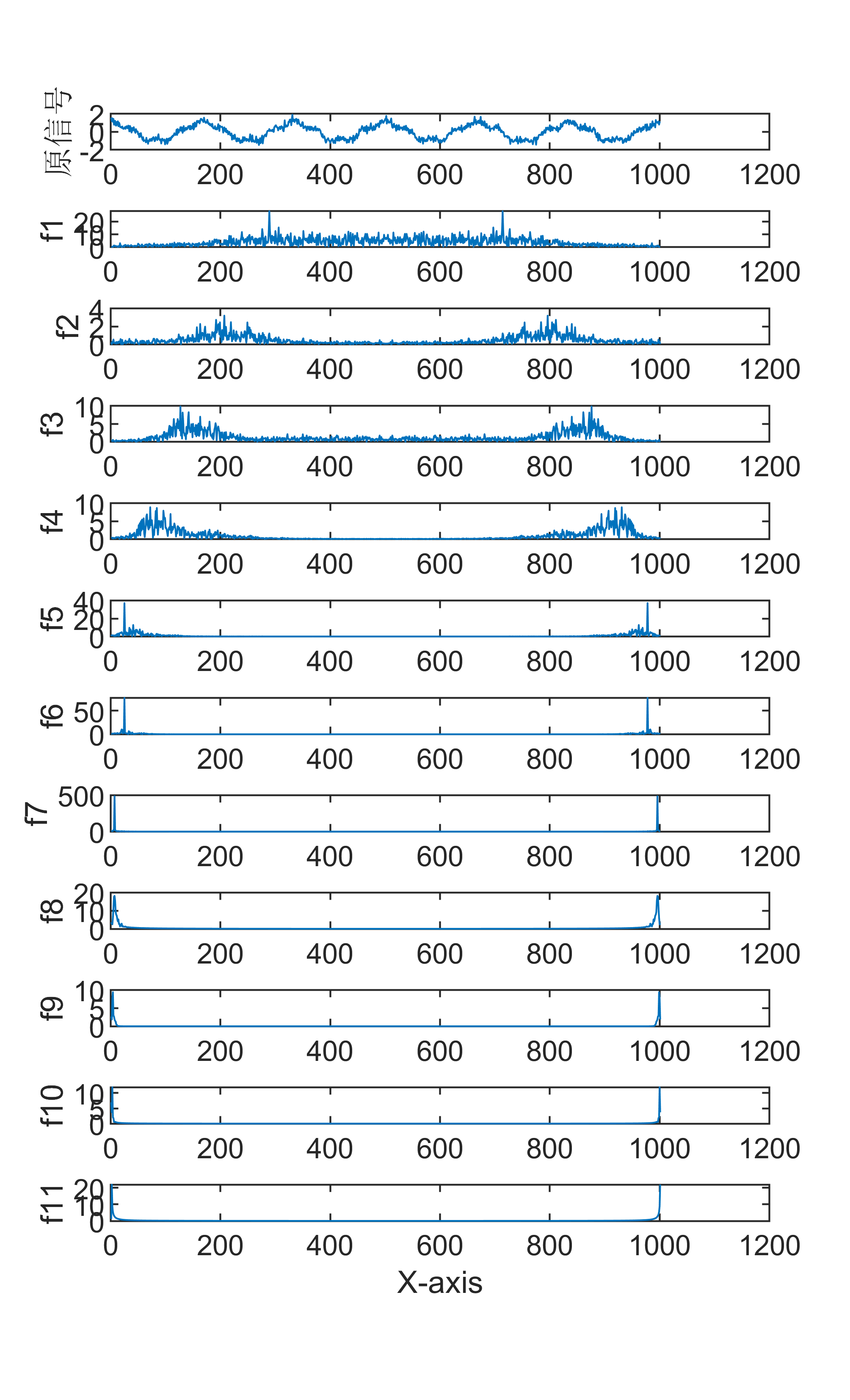
原始数据分解各分量示意图
傅里叶变换是一种数学方法,用于将一个信号分解成一系列正弦和余弦函数的和,从而更好地理解和处理信号。傅里叶变换在信号处理领域有着广泛的应用,包括音频处理、图像处理等。 具体来说,傅里叶变换的步骤如下:
-
给定一个连续时间域函数f(t),其中t为时间。
-
对f(t)进行傅里叶变换,得到它的频率域表示F(ω),其中ω为角频率。
-
F(ω)表示了f(t)中所有频率分量的幅度和相位信息。
-
将F(ω)分解成一系列正弦和余弦函数的和,即: F(ω) = ∑[a(k)cos(kω) + b(k)sin(kω)] 其中,k为频率分量的序号,a(k)和b(k)分别为对应的正弦和余弦函数的系数。 傅里叶变换的优点是可以将时间域中的信号转换成频率域中的信号,从而更好地理解信号的频率分量和周期性特征,同时也方便进行一些信号处理任务,例如滤波、降噪等。缺点是傅里叶变换需要对整个信号进行处理,计算量较大,在实时处理等场景下可能会存在较大的延迟。

6【MATLAB】小波分解信号分解+FFT傅里叶频谱变换联合算法
小波分解算法是一种数学方法,用于将信号分解为不同频率的小波成分。这种算法基于小波函数,可以用于信号处理、图像压缩和数据压缩等领域。小波分解算法的基本思想是将一个信号分解成多个小波子带,每个小波子带代表了一个不同频率的小波成分。这些小波子带可以分别进行处理,例如滤波、降采样等操作,然后再进行重构,得到原始信号。小波分解算法的优点是可以提供更好的时频分辨率,对于瞬态信号和非平稳信号的处理效果更好。同时,小波分解算法也可以用于图像压缩和数据压缩,因为小波分解后的子带可以选择性地保留或舍弃,从而实现数据压缩。总之,小波分解算法是一种强大的信号处理技术,被广泛应用于信号处理、图像压缩和数据压缩等领域。
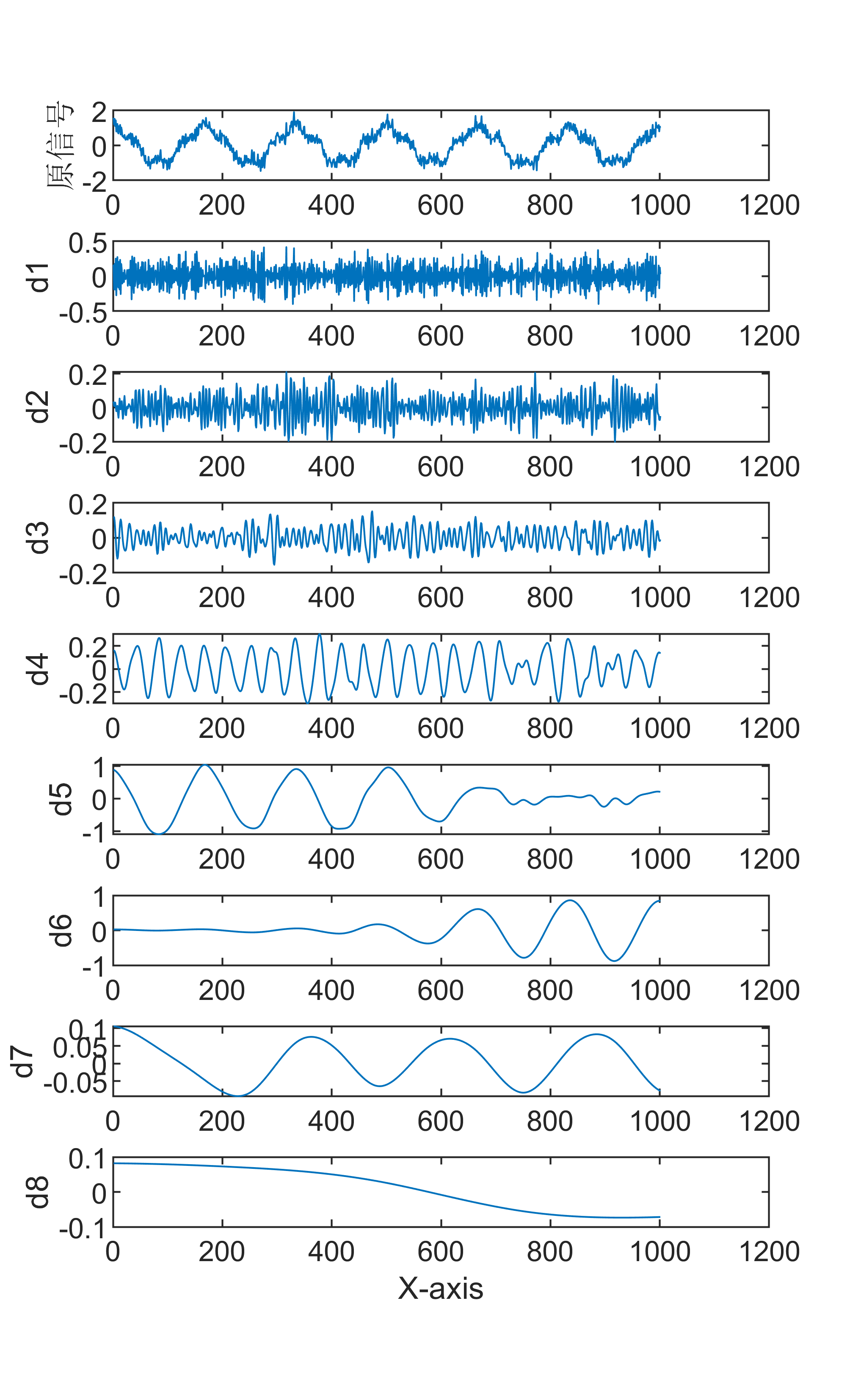
原始数据分解各分量示意图
傅里叶变换是一种数学方法,用于将一个信号分解成一系列正弦和余弦函数的和,从而更好地理解和处理信号。傅里叶变换在信号处理领域有着广泛的应用,包括音频处理、图像处理等。 具体来说,傅里叶变换的步骤如下:
-
给定一个连续时间域函数f(t),其中t为时间。
-
对f(t)进行傅里叶变换,得到它的频率域表示F(ω),其中ω为角频率。
-
F(ω)表示了f(t)中所有频率分量的幅度和相位信息。
-
将F(ω)分解成一系列正弦和余弦函数的和,即: F(ω) = ∑[a(k)cos(kω) + b(k)sin(kω)] 其中,k为频率分量的序号,a(k)和b(k)分别为对应的正弦和余弦函数的系数。 傅里叶变换的优点是可以将时间域中的信号转换成频率域中的信号,从而更好地理解信号的频率分量和周期性特征,同时也方便进行一些信号处理任务,例如滤波、降噪等。缺点是傅里叶变换需要对整个信号进行处理,计算量较大,在实时处理等场景下可能会存在较大的延迟。
7【MATLAB】VMD信号分解+FFT傅里叶频谱变换联合算法
VMD是一种新型的信号分解方法,它是通过使用变分推断方法将信号分解为一组局部振动模式,每个模式包含多个频率组件。VMD的主要步骤如下:
-
将原始信号进行多次低通滤波,得到多个频带信号。
-
对每个频带信号进行变分推断,得到该频带信号的局部振动模式。
-
将所有频带信号对应的局部振动模式相加,得到原始信号的 VMD 分解。 VMD 分解具有以下优点:能够自动提取信号的局部特征,避免了传统分解方法中需要手动选择基函数的问题;能够处理非线性和非平稳信号,并且不会产生模态重叠的问题。因此,VMD 在信号处理、图像处理和模式识别等领域也得到了广泛的应用。
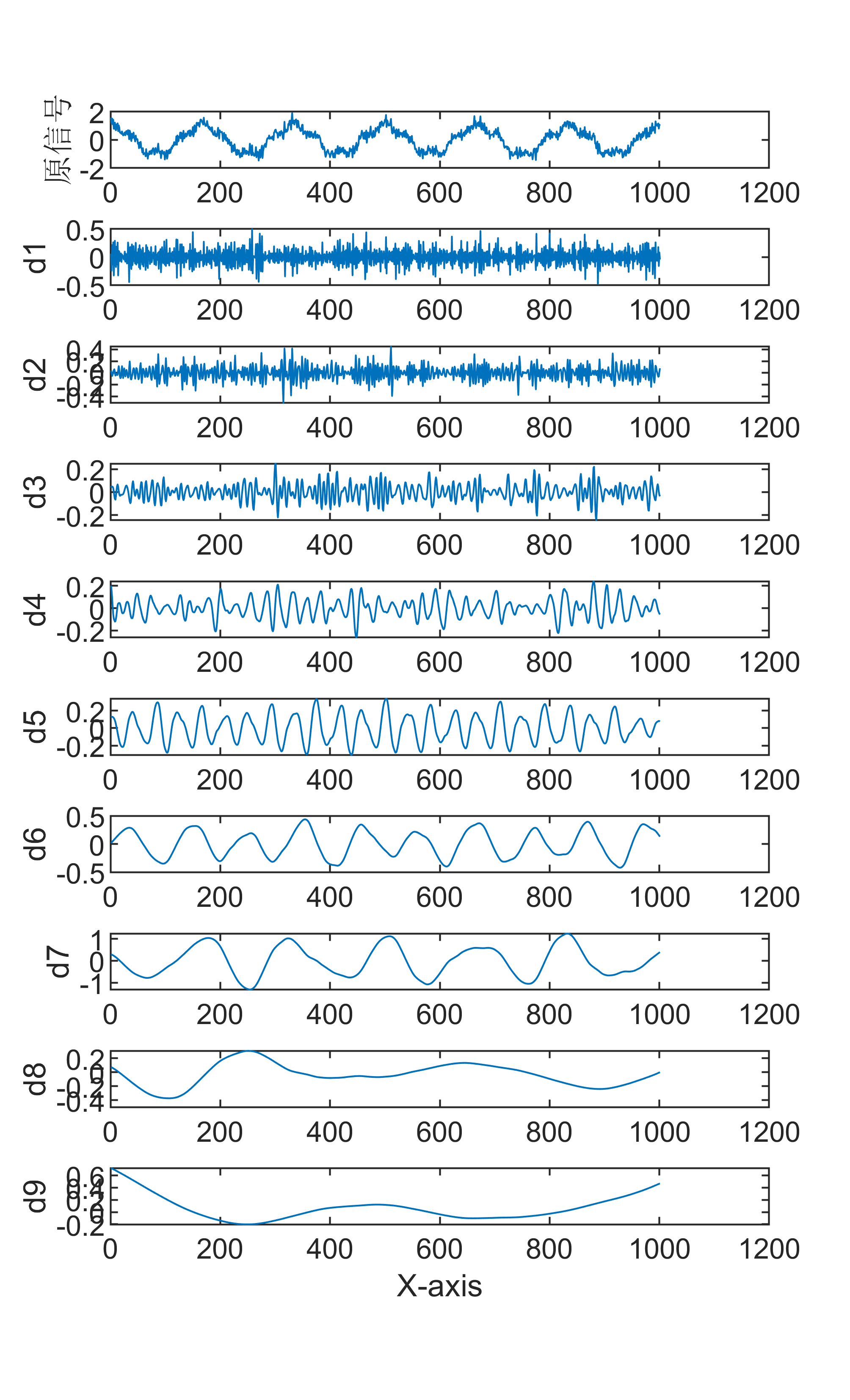
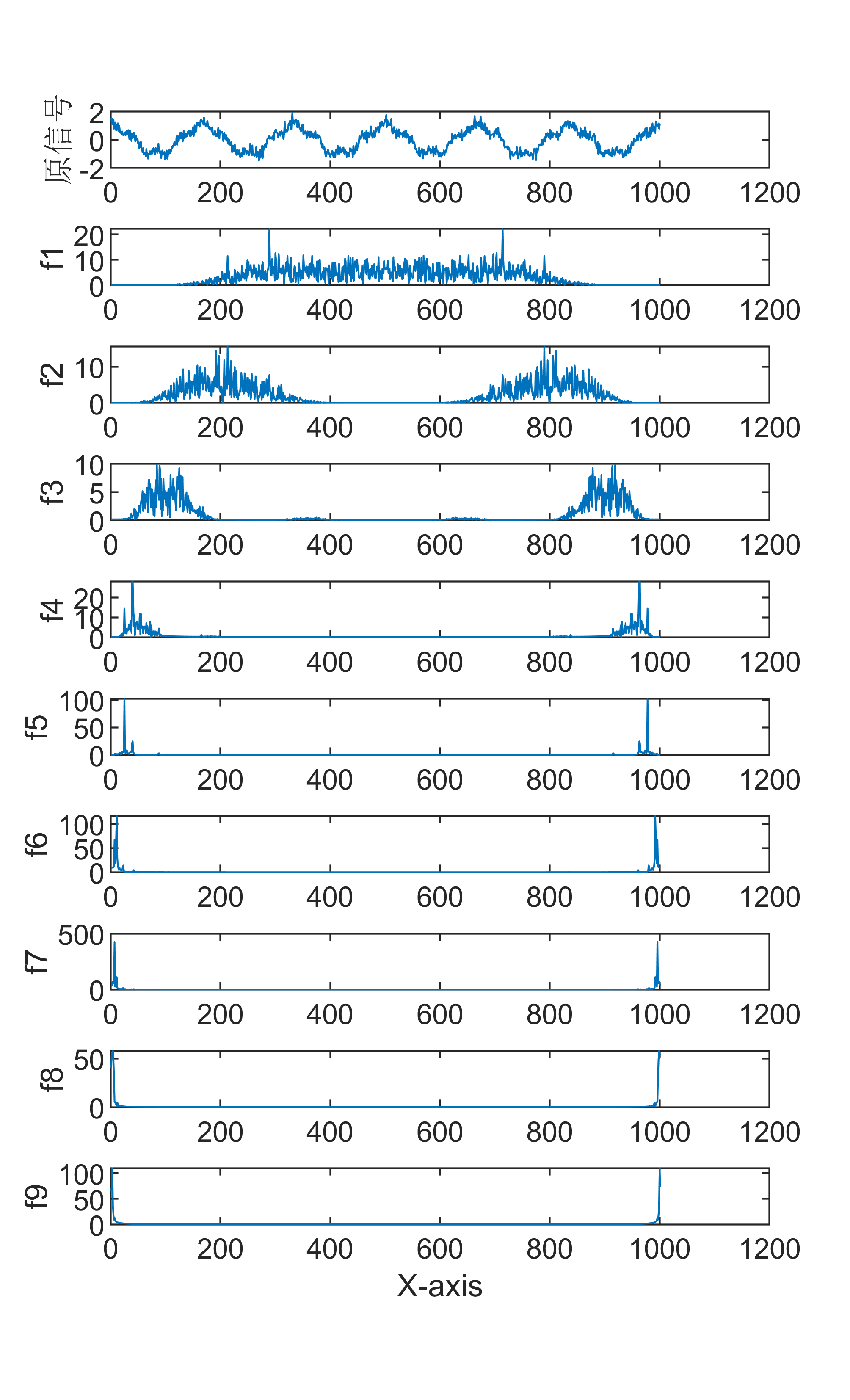
原始数据分解各分量示意图
傅里叶变换是一种数学方法,用于将一个信号分解成一系列正弦和余弦函数的和,从而更好地理解和处理信号。傅里叶变换在信号处理领域有着广泛的应用,包括音频处理、图像处理等。 具体来说,傅里叶变换的步骤如下:
-
给定一个连续时间域函数f(t),其中t为时间。
-
对f(t)进行傅里叶变换,得到它的频率域表示F(ω),其中ω为角频率。
-
F(ω)表示了f(t)中所有频率分量的幅度和相位信息。
-
将F(ω)分解成一系列正弦和余弦函数的和,即: F(ω) = ∑[a(k)cos(kω) + b(k)sin(kω)] 其中,k为频率分量的序号,a(k)和b(k)分别为对应的正弦和余弦函数的系数。 傅里叶变换的优点是可以将时间域中的信号转换成频率域中的信号,从而更好地理解信号的频率分量和周期性特征,同时也方便进行一些信号处理任务,例如滤波、降噪等。缺点是傅里叶变换需要对整个信号进行处理,计算量较大,在实时处理等场景下可能会存在较大的延迟。

8【MATLAB】LMD信号分解+FFT傅里叶频谱变换联合算法
LMD (Local Mean Decomposition) 分解算法是一种信号分解算法,它可以将一个信号分解成多个局部平滑的成分,并且可以将高频噪声和低频信号有效地分离出来。LMD 分解算法是一种自适应的分解方法,可以根据信号的局部特征来进行分解,从而提高了分解的精度和效果。 LMD 分解算法的基本思想是,在原始信号中选取局部的极大值点和极小值点,然后通过这些极值点之间的平均值来计算一个局部平滑的成分。这个过程可以迭代进行,直到得到所有的局部平滑的成分。最后,将这些局部平滑的成分加起来,即可得到原始信号的分解结果。 LMD 分解算法具有以下优点:
-
自适应性强:LMD 分解算法可以根据信号的局部特征来进行分解,从而提高了分解的精度和效果。
-
分解精度高:LMD 分解算法可以将高频噪声和低频信号有效地分离出来,从而提高了分解的精度。
-
计算效率高:LMD 分解算法的计算量较小,可以快速地进行信号分解。总之,LMD 分解算法是一种高效、精确、自适应的信号分解算法,被广泛应用于信号处理、图像处理、语音处理等领域。
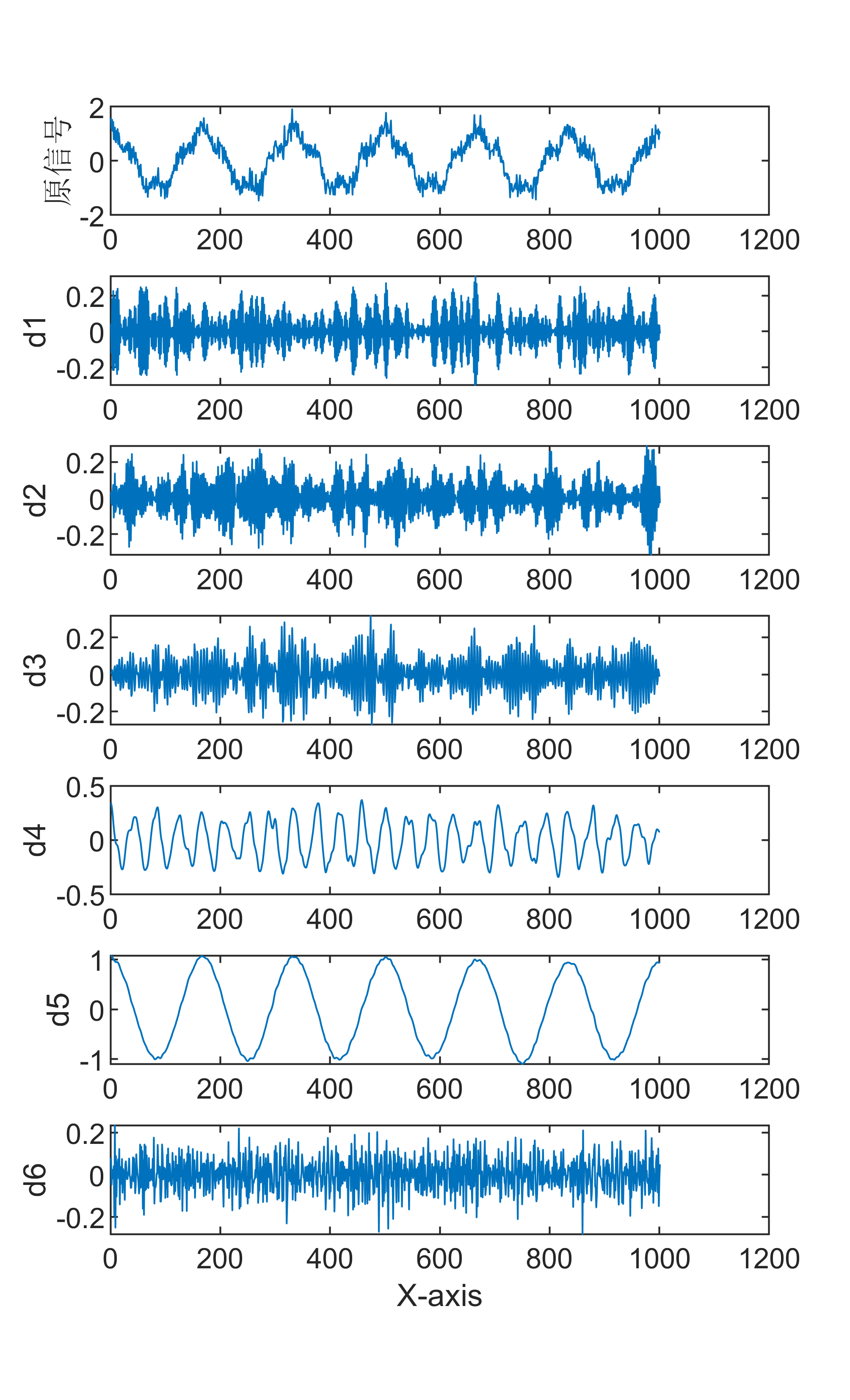
原始数据分解各分量示意图
傅里叶变换是一种数学方法,用于将一个信号分解成一系列正弦和余弦函数的和,从而更好地理解和处理信号。傅里叶变换在信号处理领域有着广泛的应用,包括音频处理、图像处理等。 具体来说,傅里叶变换的步骤如下:
-
给定一个连续时间域函数f(t),其中t为时间。
-
对f(t)进行傅里叶变换,得到它的频率域表示F(ω),其中ω为角频率。
-
F(ω)表示了f(t)中所有频率分量的幅度和相位信息。
-
将F(ω)分解成一系列正弦和余弦函数的和,即: F(ω) = ∑[a(k)cos(kω) + b(k)sin(kω)] 其中,k为频率分量的序号,a(k)和b(k)分别为对应的正弦和余弦函数的系数。 傅里叶变换的优点是可以将时间域中的信号转换成频率域中的信号,从而更好地理解信号的频率分量和周期性特征,同时也方便进行一些信号处理任务,例如滤波、降噪等。缺点是傅里叶变换需要对整个信号进行处理,计算量较大,在实时处理等场景下可能会存在较大的延迟。
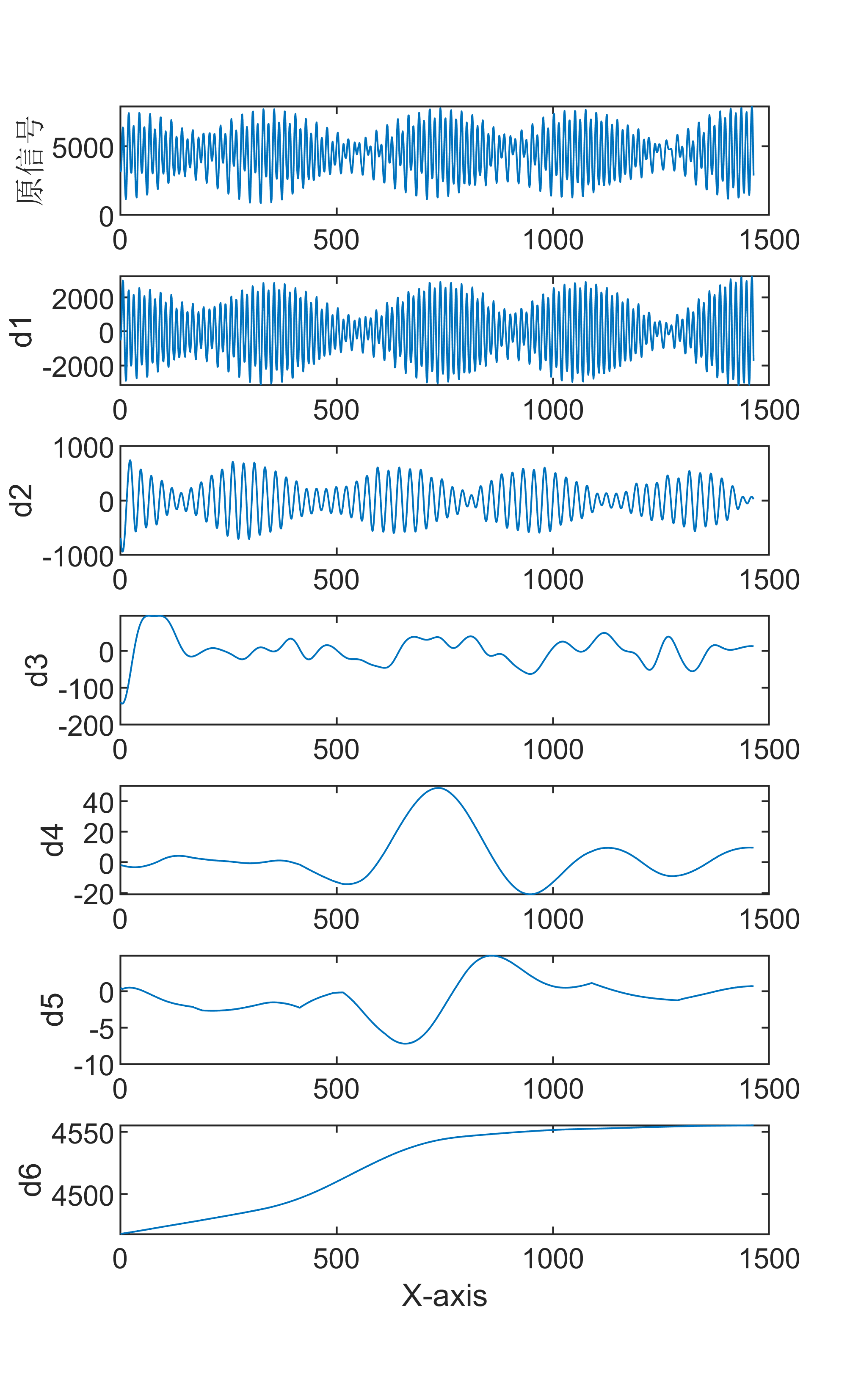
9【MATLAB】RLMD信号分解+FFT傅里叶频谱变换联合算法
RLMD(Robust Local Mode Decomposition)是一种鲁棒的局部模态分解方法。它是通过在局部区间内对信号进行多项式拟合,提取局部特征,进而分解信号为多个局部模态函数的和。RLMD的主要步骤如下:
-
将原始信号分段,对每个局部区间内的信号进行多项式拟合,得到该局部区间的局部趋势。
-
将原始信号减去该局部区间的局部趋势,得到该局部区间内的局部振动模式。
-
对每个局部振动模式,重复步骤1和2,直到该局部振动模式变为平稳信号,得到该局部区间内的局部模态函数。
-
将所有局部区间内的局部模态函数相加,得到原始信号的 RLMD 分解。 RLMD 分解具有对噪声和异常值的鲁棒性,能够更准确地分解信号。同时,RLMD 还能够处理非平稳信号,具有较好的局部性和自适应性。因此,RLMD 在信号处理、图像处理和模式识别等领域也得到了广泛的应用。
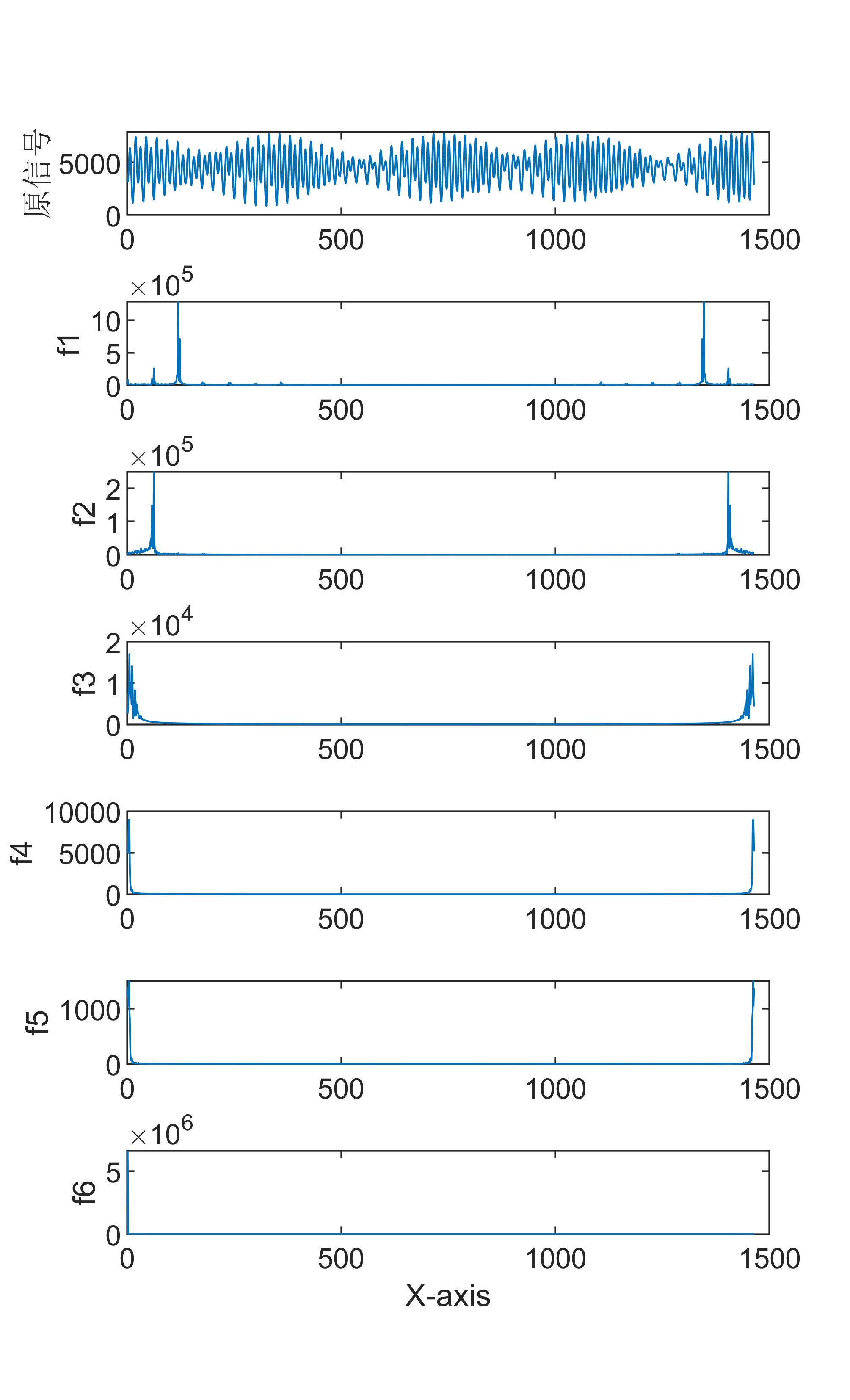
原始数据分解各分量示意图

傅里叶变换是一种数学方法,用于将一个信号分解成一系列正弦和余弦函数的和,从而更好地理解和处理信号。傅里叶变换在信号处理领域有着广泛的应用,包括音频处理、图像处理等。 具体来说,傅里叶变换的步骤如下:
-
给定一个连续时间域函数f(t),其中t为时间。
-
对f(t)进行傅里叶变换,得到它的频率域表示F(ω),其中ω为角频率。
-
F(ω)表示了f(t)中所有频率分量的幅度和相位信息。
-
将F(ω)分解成一系列正弦和余弦函数的和,即: F(ω) = ∑[a(k)cos(kω) + b(k)sin(kω)] 其中,k为频率分量的序号,a(k)和b(k)分别为对应的正弦和余弦函数的系数。 傅里叶变换的优点是可以将时间域中的信号转换成频率域中的信号,从而更好地理解信号的频率分量和周期性特征,同时也方便进行一些信号处理任务,例如滤波、降噪等。缺点是傅里叶变换需要对整个信号进行处理,计算量较大,在实时处理等场景下可能会存在较大的延迟。

10【MATLAB】EWT 信号分解+FFT傅里叶频谱变换联合算法
EWT (Empirical Wavelet Transform) 分解算法是一种用于信号分解的方法,它可以将信号分解成多个局部频率的小波成分,从而实现对信号的高效处理和分析。EWT 分解算法基于小波分析和自适应滤波器,可以适应不同类型的信号,并且能够处理非平稳信号和非线性信号。 EWT 分解算法的基本思想是,首先将信号分解成多个局部频率的小波成分,然后通过自适应滤波器对每个小波成分进行去噪和平滑处理,最后将处理后的小波成分合并起来得到原始信号的分解结果。 EWT 分解算法具有以下优点:
-
适应性强:EWT 分解算法可以适应不同类型的信号,并且能够处理非平稳信号和非线性信号。
-
分解精度高:EWT 分解算法可以将信号分解成多个局部频率的小波成分,从而提高了分解的精度。
-
计算效率高:EWT 分解算法的计算量较小,可以快速地进行信号分解。总之,EWT 分解算法是一种高效、精确、适应性强的信号分解算法,被广泛应用于信号处理、图像处理、语音处理等领域。
原始数据分解各分量示意图

傅里叶变换是一种数学方法,用于将一个信号分解成一系列正弦和余弦函数的和,从而更好地理解和处理信号。傅里叶变换在信号处理领域有着广泛的应用,包括音频处理、图像处理等。 具体来说,傅里叶变换的步骤如下:
-
给定一个连续时间域函数f(t),其中t为时间。
-
对f(t)进行傅里叶变换,得到它的频率域表示F(ω),其中ω为角频率。
-
F(ω)表示了f(t)中所有频率分量的幅度和相位信息。
-
将F(ω)分解成一系列正弦和余弦函数的和,即: F(ω) = ∑[a(k)cos(kω) + b(k)sin(kω)] 其中,k为频率分量的序号,a(k)和b(k)分别为对应的正弦和余弦函数的系数。 傅里叶变换的优点是可以将时间域中的信号转换成频率域中的信号,从而更好地理解信号的频率分量和周期性特征,同时也方便进行一些信号处理任务,例如滤波、降噪等。缺点是傅里叶变换需要对整个信号进行处理,计算量较大,在实时处理等场景下可能会存在较大的延迟。
11【MATLAB】MLPTDenoise信号分解+FFT傅里叶频谱变换联合算法
MLPTDenoise(Multi-Level and Multi-Scale Principal Trend Denoising)是一种多级、多尺度主导趋势去噪方法。它是通过将信号分解为多个层次和尺度的主导趋势,进而去除噪声和冗余信息。MLPTDenoise的主要步骤如下:
-
对原始信号进行小波变换,得到多个尺度的小波系数。
-
对每个小波系数进行主导趋势分解,得到该尺度上的主导趋势和细节信号。
-
将每个尺度的主导趋势相加,得到该层次的主导趋势。
-
将该层次的主导趋势作为信号的一部分,将细节信号作为噪声,对噪声进行滤波去除。
-
将去除噪声后的信号进行重构,得到该层次的去噪信号。
-
重复步骤 2~5,直到所有层次的信号都被分解和去噪,得到原始信号的 MLPTDenoise 分解。 MLPTDenoise 分解具有对噪声和冗余信息的较好抑制效果,同时能够保留信号的主导趋势信息,避免了传统方法中的信号失真问题。因此,MLPTDenoise 在信号处理、图像处理和模式识别等领域也得到了广泛的应用。
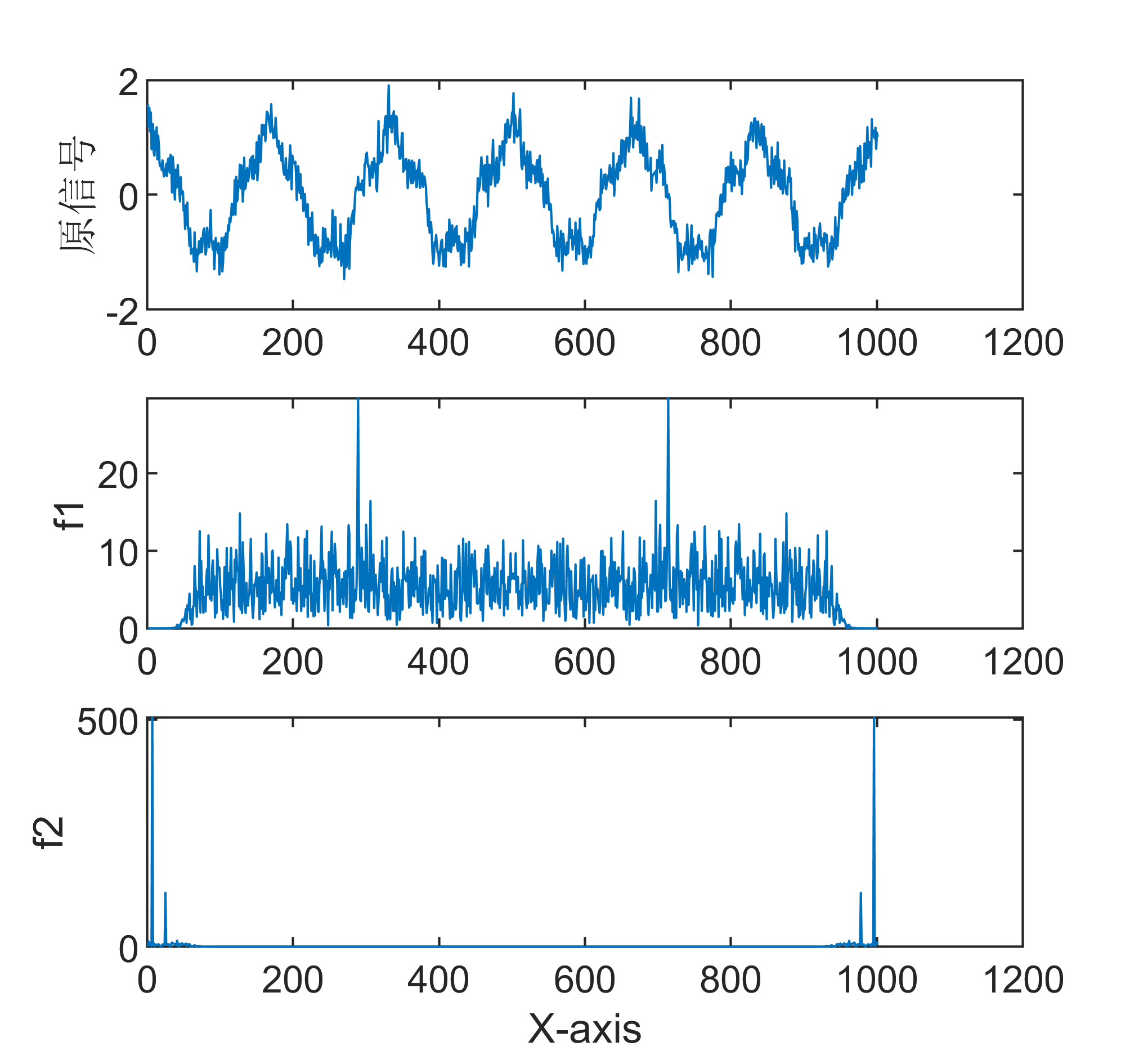
原始数据分解各分量示意图

傅里叶变换是一种数学方法,用于将一个信号分解成一系列正弦和余弦函数的和,从而更好地理解和处理信号。傅里叶变换在信号处理领域有着广泛的应用,包括音频处理、图像处理等。 具体来说,傅里叶变换的步骤如下:
-
给定一个连续时间域函数f(t),其中t为时间。
-
对f(t)进行傅里叶变换,得到它的频率域表示F(ω),其中ω为角频率。
-
F(ω)表示了f(t)中所有频率分量的幅度和相位信息。
-
将F(ω)分解成一系列正弦和余弦函数的和,即: F(ω) = ∑[a(k)cos(kω) + b(k)sin(kω)] 其中,k为频率分量的序号,a(k)和b(k)分别为对应的正弦和余弦函数的系数。 傅里叶变换的优点是可以将时间域中的信号转换成频率域中的信号,从而更好地理解信号的频率分量和周期性特征,同时也方便进行一些信号处理任务,例如滤波、降噪等。缺点是傅里叶变换需要对整个信号进行处理,计算量较大,在实时处理等场景下可能会存在较大的延迟。
12【MATLAB】MODWT信号分解+FFT傅里叶频谱变换联合算法
MODWT(Maximal Overlap Discrete Wavelet Transform)是一种最大重叠离散小波变换方法,它是通过多级小波分解,将信号分解为不同尺度和频率的小波系数。MODWT的主要步骤如下:
-
对原始信号进行多级小波分解,得到多个尺度和频率的小波系数。
-
对每个尺度的小波系数进行重构,得到重构系数。
-
对每个尺度的重构系数进行小波变换,得到该尺度的小波系数。
-
将所有尺度的小波系数相加,得到原始信号的 MODWT 分解。 MODWT 分解具有对信号的多尺度分析能力,能够提供不同尺度和频率的信号信息。同时,MODWT 还能够避免传统小波变换中的信号失真问题,具有比较好的重构能力。因此,MODWT 在信号处理、图像处理和模式识别等领域也得到了广泛的应用。
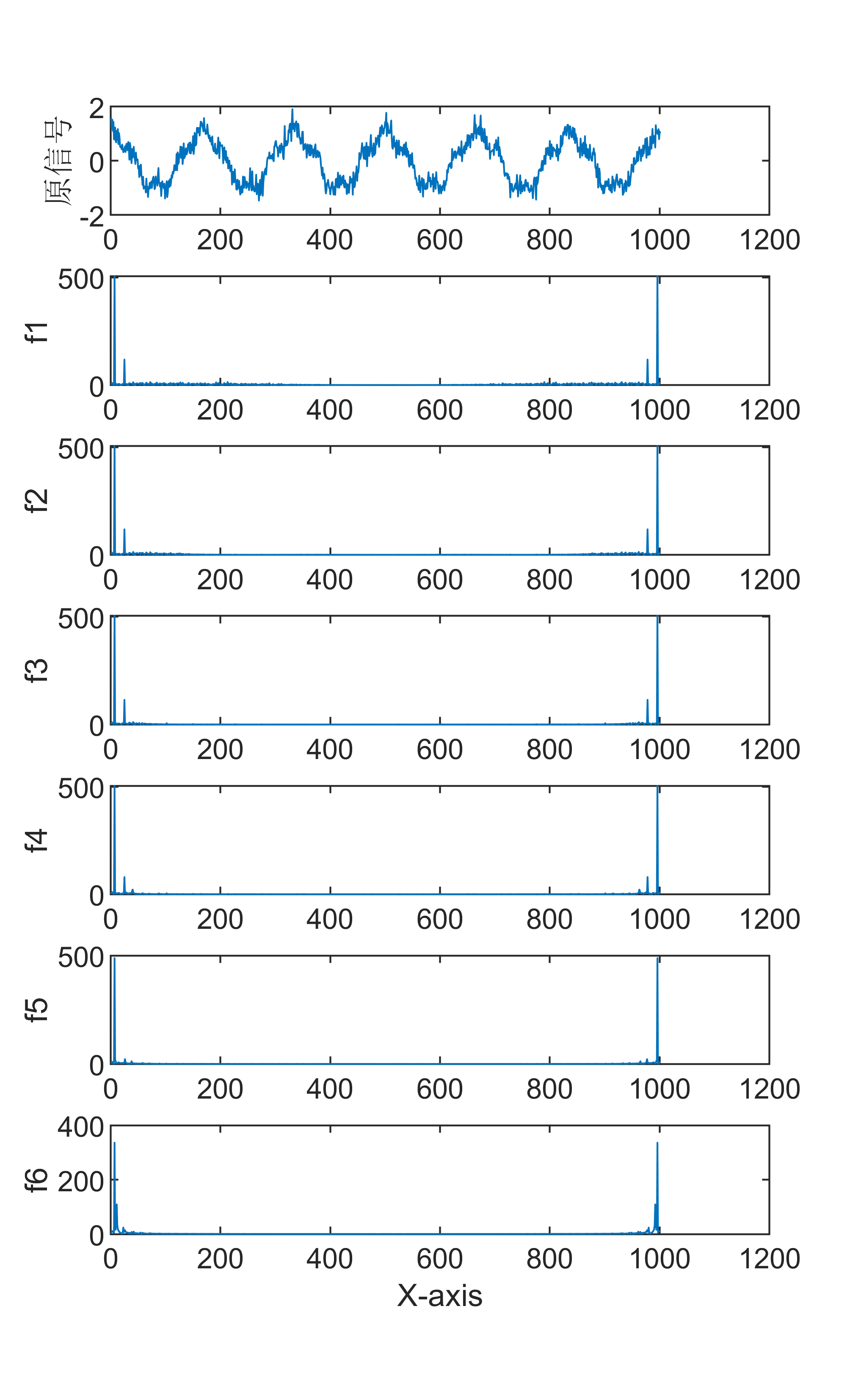
原始数据分解各分量示意图
傅里叶变换是一种数学方法,用于将一个信号分解成一系列正弦和余弦函数的和,从而更好地理解和处理信号。傅里叶变换在信号处理领域有着广泛的应用,包括音频处理、图像处理等。 具体来说,傅里叶变换的步骤如下:
-
给定一个连续时间域函数f(t),其中t为时间。
-
对f(t)进行傅里叶变换,得到它的频率域表示F(ω),其中ω为角频率。
-
F(ω)表示了f(t)中所有频率分量的幅度和相位信息。
-
将F(ω)分解成一系列正弦和余弦函数的和,即: F(ω) = ∑[a(k)cos(kω) + b(k)sin(kω)] 其中,k为频率分量的序号,a(k)和b(k)分别为对应的正弦和余弦函数的系数。 傅里叶变换的优点是可以将时间域中的信号转换成频率域中的信号,从而更好地理解信号的频率分量和周期性特征,同时也方便进行一些信号处理任务,例如滤波、降噪等。缺点是傅里叶变换需要对整个信号进行处理,计算量较大,在实时处理等场景下可能会存在较大的延迟。
13【MATLAB】辛几何模态分解信号分解+FFT傅里叶频谱变换联合算法
辛几何模态分解(Symplectic Modal Analysis,SMA)是一种用于辛结构系统(如机械系统、光学系统等)振动分析的方法。它基于辛几何理论和模态分析方法,能够在保持系统辛结构的前提下,分解系统振动模态,并得到相应的振动频率和阻尼比。具体来说,辛几何模态分解首先将辛结构系统的运动方程转化为哈密尔顿形式,并通过辛几何积分方法求解系统的运动轨迹。然后,通过对系统轨迹进行奇异值分解(SVD),可以得到系统的振动模态及其阻尼比和振动频率。相比于传统的有限元方法,辛几何模态分解能够更准确地描述系统的振动行为,并且可以避免传统方法中出现的不物理的振动模态。辛几何模态分解在机械系统、光学系统、天体力学等领域有着广泛的应用,例如用于光学望远镜的振动分析、用于机械系统的结构优化等。
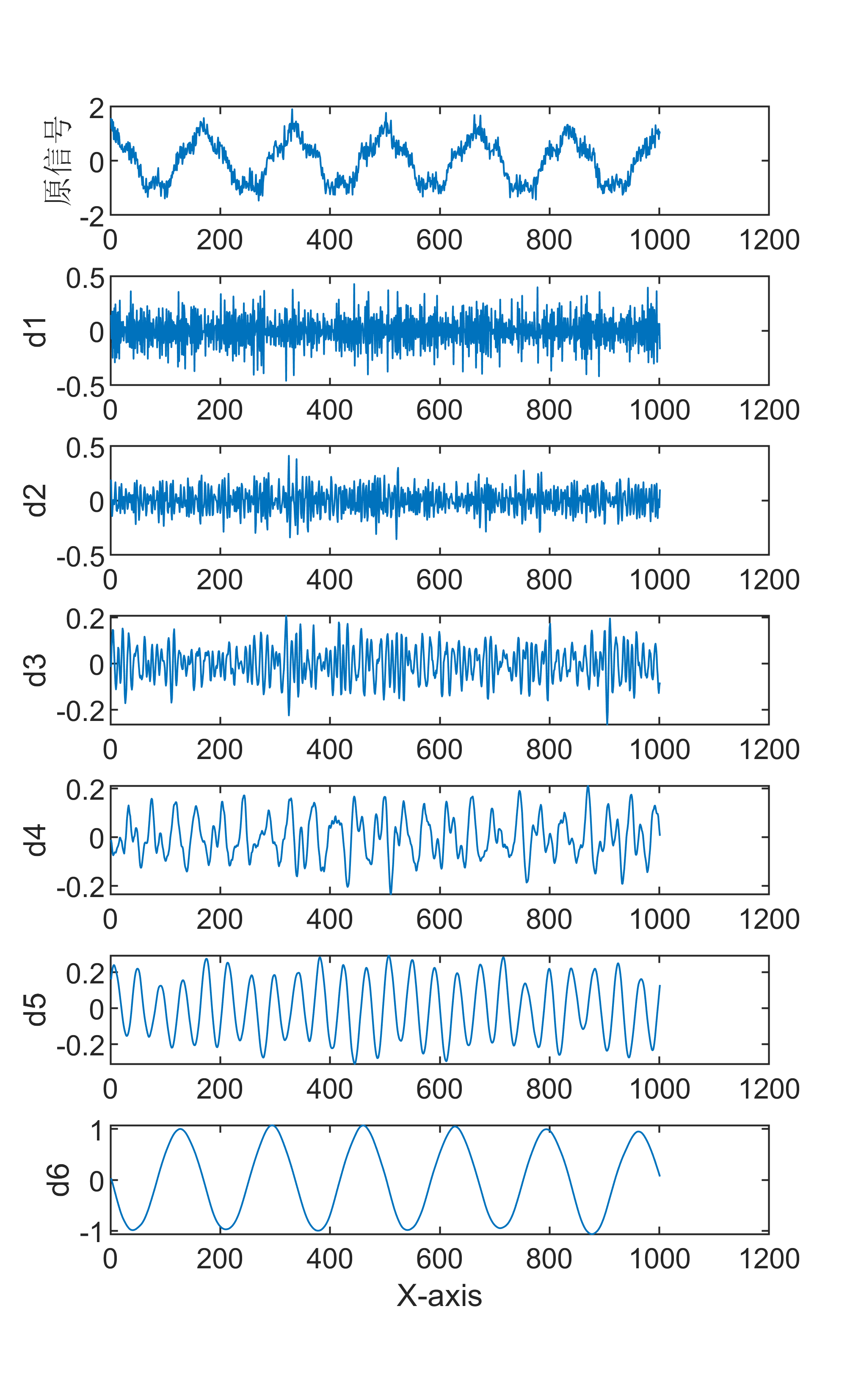
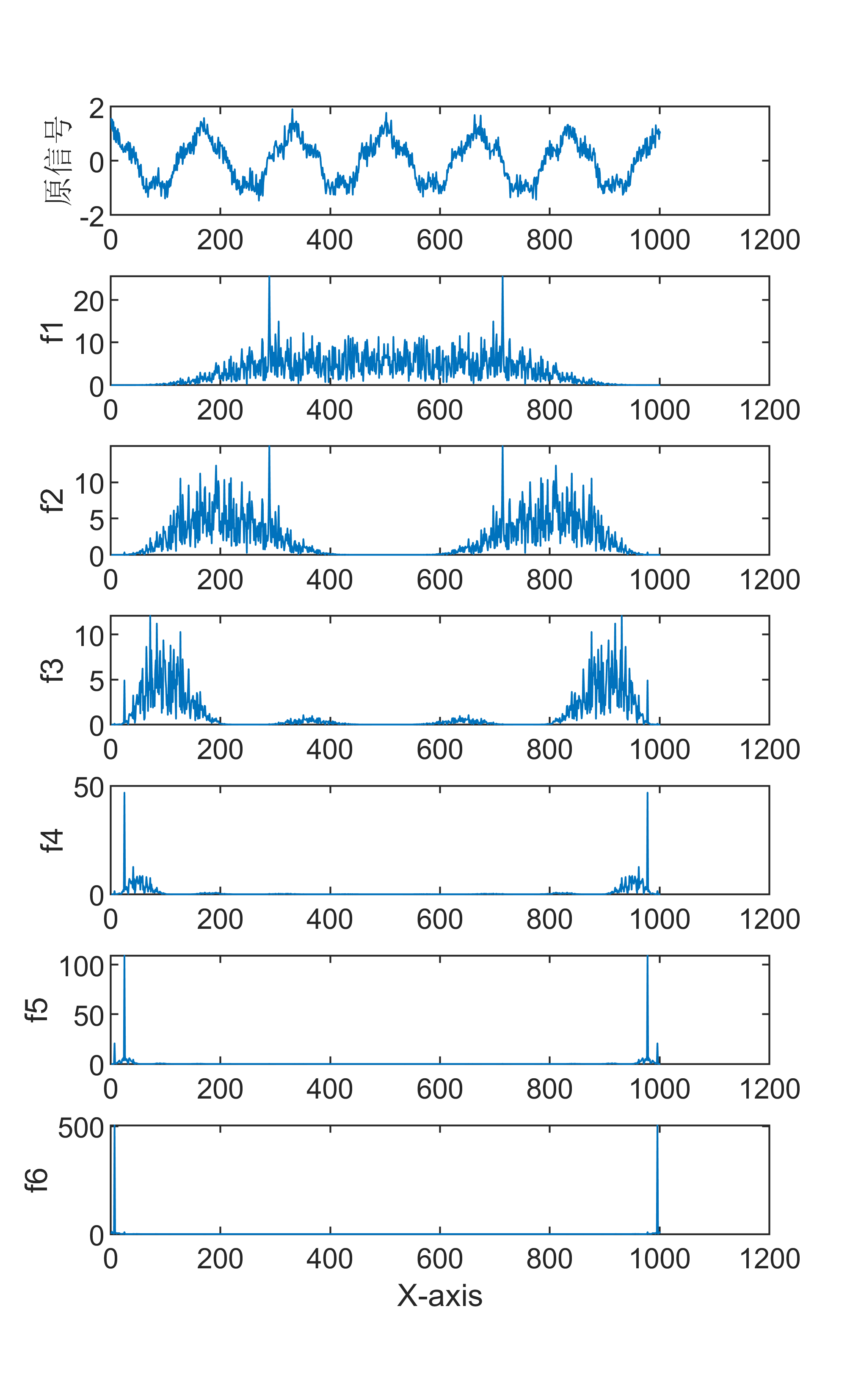
原始数据分解各分量示意图
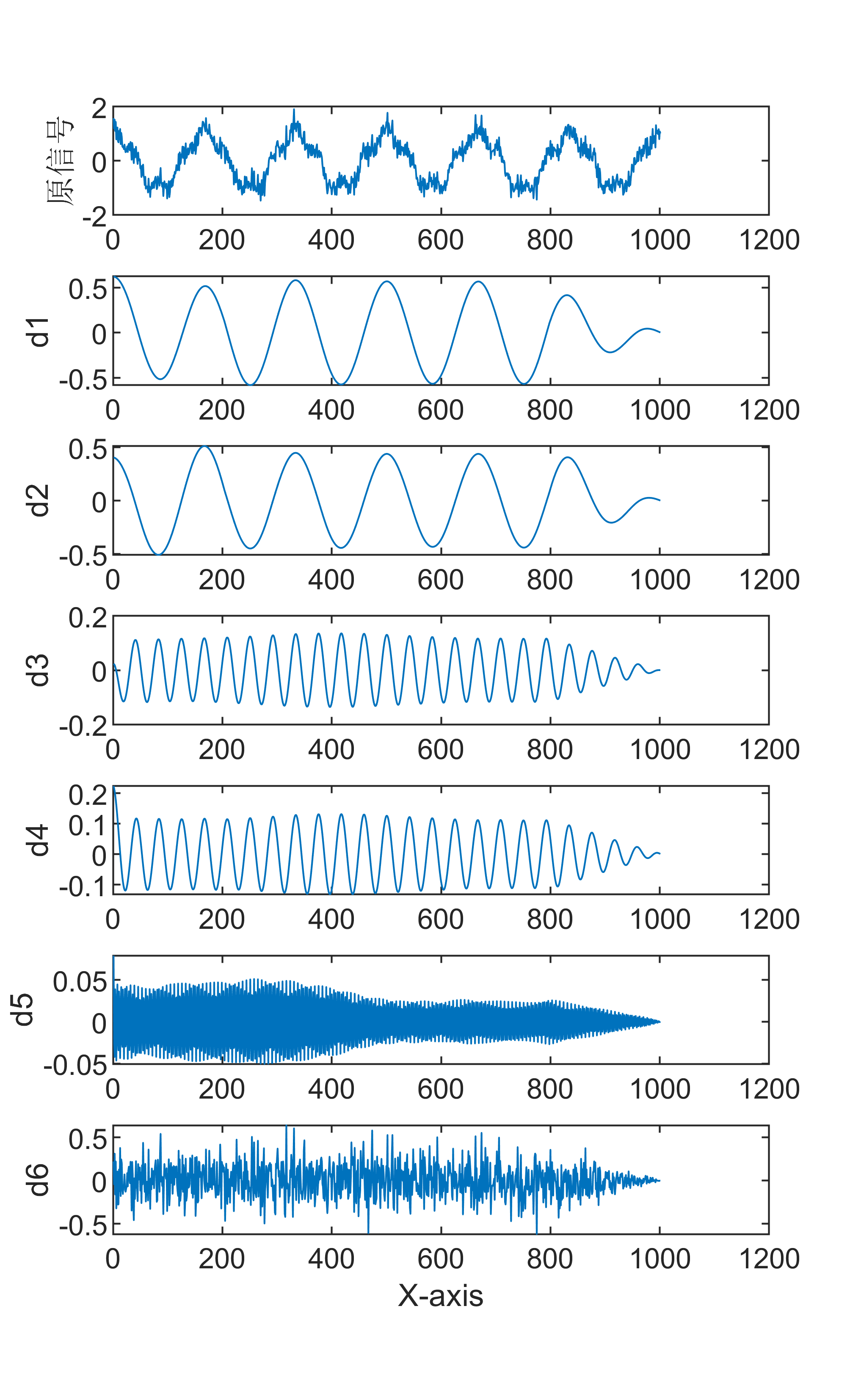
傅里叶变换是一种数学方法,用于将一个信号分解成一系列正弦和余弦函数的和,从而更好地理解和处理信号。傅里叶变换在信号处理领域有着广泛的应用,包括音频处理、图像处理等。 具体来说,傅里叶变换的步骤如下:
-
给定一个连续时间域函数f(t),其中t为时间。
-
对f(t)进行傅里叶变换,得到它的频率域表示F(ω),其中ω为角频率。
-
F(ω)表示了f(t)中所有频率分量的幅度和相位信息。
-
将F(ω)分解成一系列正弦和余弦函数的和,即: F(ω) = ∑[a(k)cos(kω) + b(k)sin(kω)] 其中,k为频率分量的序号,a(k)和b(k)分别为对应的正弦和余弦函数的系数。 傅里叶变换的优点是可以将时间域中的信号转换成频率域中的信号,从而更好地理解信号的频率分量和周期性特征,同时也方便进行一些信号处理任务,例如滤波、降噪等。缺点是傅里叶变换需要对整个信号进行处理,计算量较大,在实时处理等场景下可能会存在较大的延迟。

【MATLAB】全网唯一的13种信号分解+FFT傅里叶频谱变换联合算法全家桶
具体算法获取见文章顶部~
相关文章:

【MATLAB】全网唯一的13种信号分解+FFT傅里叶频谱变换联合算法全家桶
有意向获取代码,请转文末观看代码获取方式~ 大家吃一顿火锅的价格便可以拥有13种信号分解FFT傅里叶频谱变换联合算法,绝对不亏,知识付费是现今时代的趋势,而且都是我精心制作的教程,有问题可随时反馈~也可单独获取某一…...
Nginx安装与配置
1.下载安装包 官网下载地址:nginx: download 可以先将安装包下载到本地再传到服务器,或者直接用wget命令将安装包下载到服务器,这里我们直接将安装包下载到服务器上。未安装wget命令的需要先安装wget,yum install -y wget [root…...

linux笔记总结-基本命令
参考: 1.Linux 和Windows比 比较 (了解) 1. 记住一句经典的话:在 Linux 世界里,一切皆文件 2. Linux目录结构 /lib • 系统开机所需要最基本的动态连接共享库,其作用类似于Windows里的DLL文件。几 乎所有…...
[PHP]禅道项目管理软件ZenTaoPMS源码包 v16.4
禅道项目管理软件ZenTaoPMS一键安装包是一款国产的开源项目管理软件。它集产品管理、项目管理、质量管理、文档管理、组织管理和事务管理于一体,是一款专业的研发项目管理软件,完整地覆盖了项目管理的核心流程。注重实效的管理思想,合理的软件…...

Required String parameter ‘name‘ is not present
[org.springframework.web.bind.MissingServletRequestParameterException: Required String parameter name is not present] 服务端有参数name,客户端没有传上来...
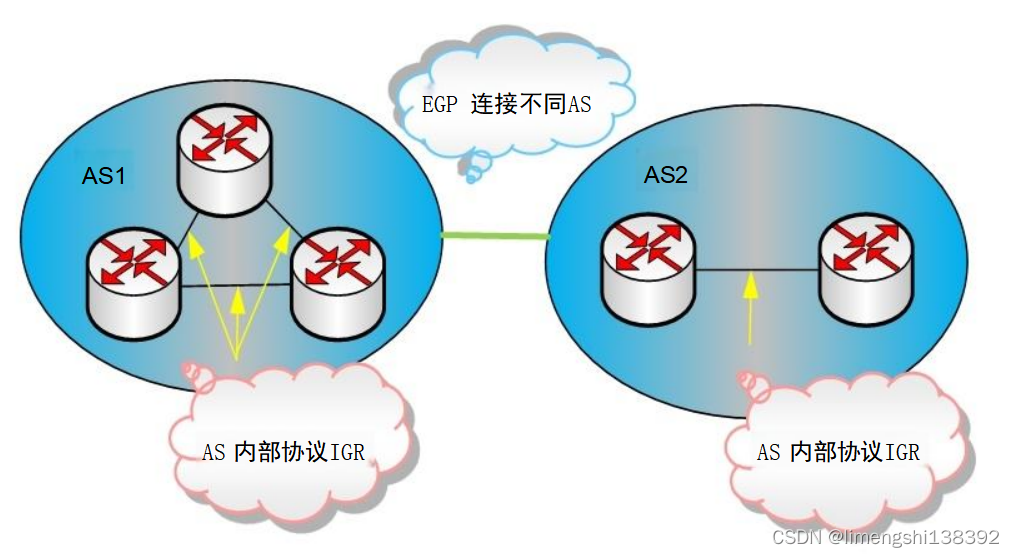
路由器基础(五): OSPF原理与配置
开放式最短路径优先 (Open Shortest Path First,OSPF) 是一个内部网关协议 (Interior Gateway Protocol,IGP),用于在单一自治系统(Autonomous System,AS) 内决策路由。OSPF 适合小型、中型、较大规模网络。OSPF 采用Dijkstra的最短路径优先算法 (Shortest Pat…...
Leetcode1128. 等价多米诺骨牌对的数量
Every day a Leetcode 题目来源:1128. 等价多米诺骨牌对的数量 解法1:暴力 代码: class Solution { public:int numEquivDominoPairs(vector<vector<int>> &dominoes){int n dominoes.size(), count 0;for (int i 0;…...
Dev-C调试的基本方法2-2
3.3 跳出函数 在图6所示的状态下,点击单步调试(F7)会继续调试下一行,而如果想结束在函数中的调试,则点击图4③所示的跳出函数,或CtrlF8按键跳出f()函数,程序将会停在图5所示的第11行处。 3.4 …...

企业之间的竞争,ISO三体系认证至关重要!
ISO三体系认证是指ISO 9001质量管理体系认证、ISO 14001环境管理体系认证、ISO 45001(OHSAS18001)职业健康安全管理体系认证。企业(组织)自愿申请、通过ISO三体系认证,并贯彻落实,确实能获益多多。 ISO 9001质量管理体系 我们经…...
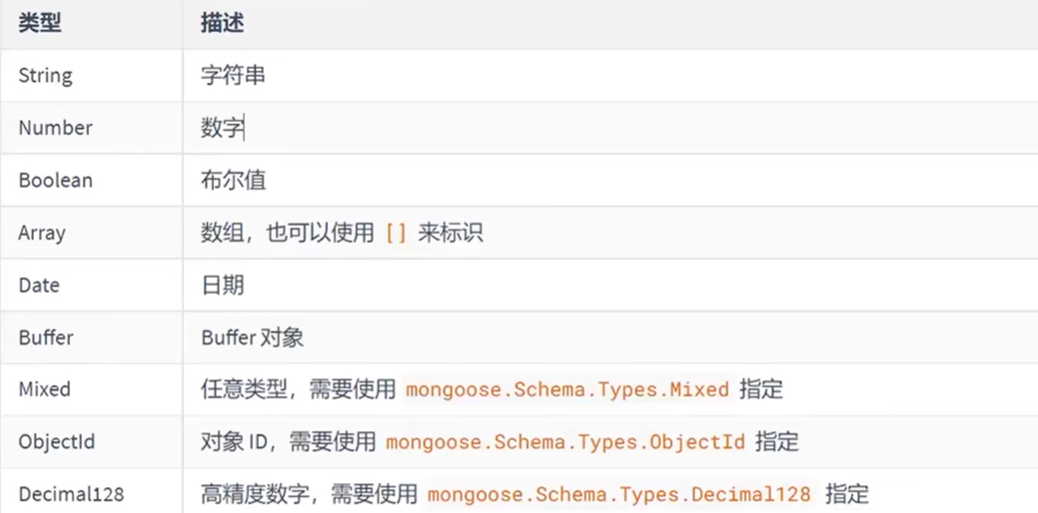
node教程(四)Mongodb+mongoose
文章目录 一、mongodb1.简介1.1Mongodb是什么?1.2数据库是什么?1.3数据库的作用1.4数据库管理数据的特点 2.核心概念3.下载安装与启动4.命令行交互4.1数据库命令4.3文档命令 二、Mongoose1.介绍2.作用3.使用流程4.插入文档5.mongoose字段类型 一、mongod…...

作为一个初学者,该如何入门大模型?
在生成式 AI 盛行的当下,你是否被这种技术所折服,例如输入一段简简单单的文字,转眼之间,一幅精美的图片,又或者是文笔流畅的文字就展现在你的面前。 相信很多人有这种想法,认为生成式 AI 深不可测…...

编译支持GPU的opencv,并供python的import cv2调用
下载opencv和opencv_contrib,cmake过程中要下载的一些包可以手动下载配置,如果网络较好,也可以等待自动下载。主要记录的是cmake命令: cmake -D CMAKE_BUILD_TYPERELEASE \-D BUILD_opencv_python3YES \-D CMAKE_INSTALL_PREFIX/…...

Bug记录
那些年写过的很小的bug: Bug1: if args.model IRNN or irnn:# some code这实际上不会按你期望的方式工作。原因在于 ‘irnn’ 是一个非空的字符串,因此它在布尔上下文中被视为 True。所以条件总是为真,而不会考虑 args.model 的…...
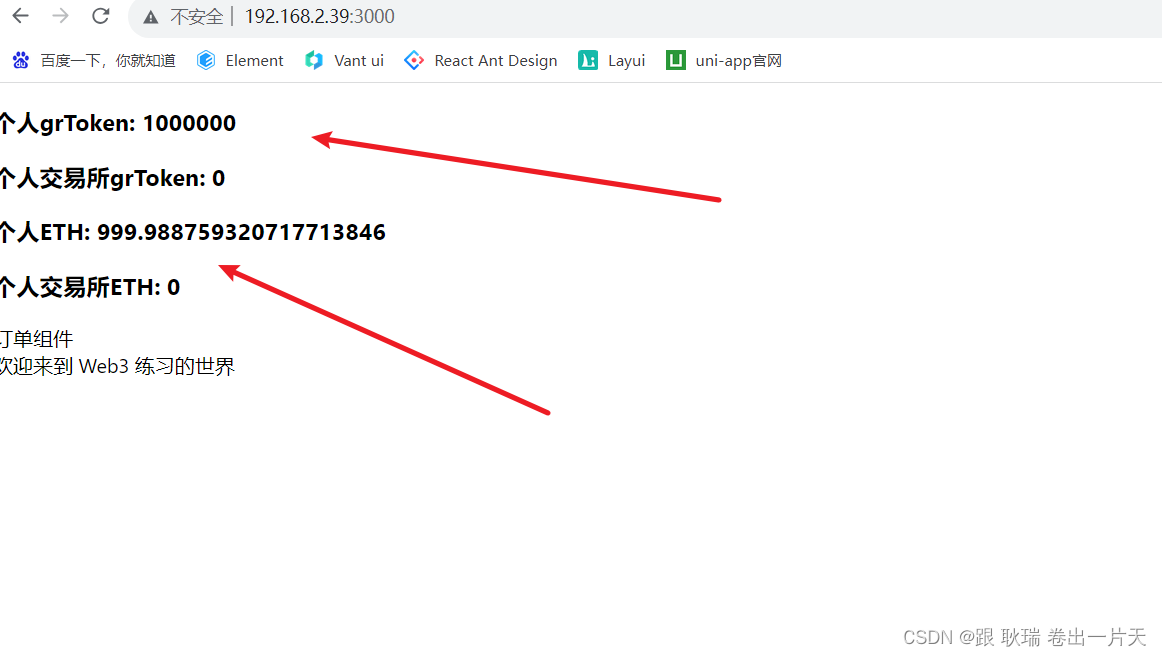
web3 React dapp中编写balance组件从redux取出并展示用户资产
好啊 上文WEB3 在 React搭建的Dapp中通过redux全局获取并存储用户ETH与自定义token与交易所存储数量中 我们拿到了用户的一个本身 和 交易所token数量 并放进了redux中做了一个全局管理 然后 我们继续 先 起来ganache的一个模拟环境 ganache -d然后 我们启动自己的项目 顺手发…...
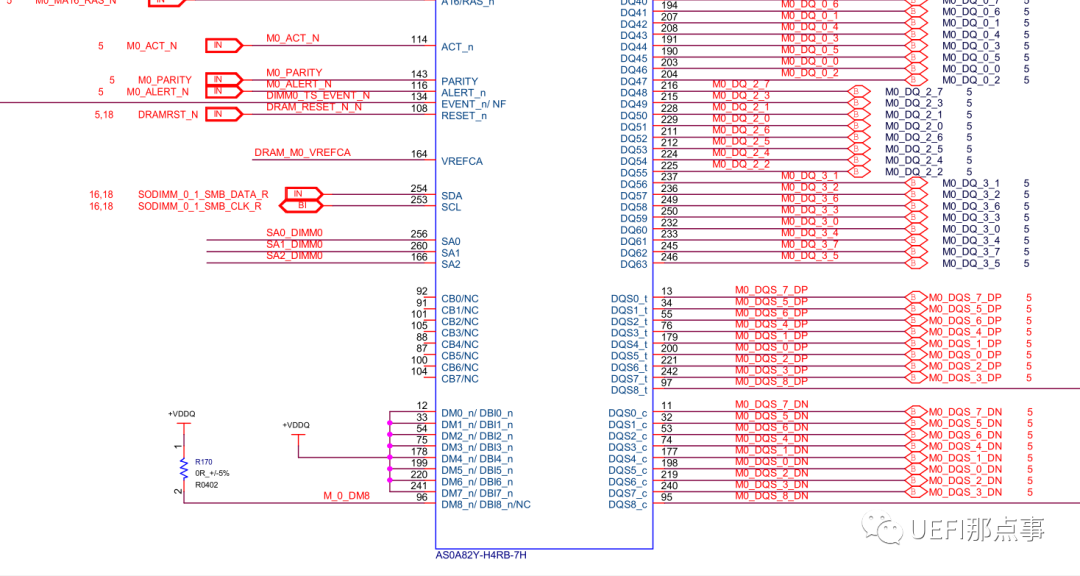
BIOS开发笔记 - DDR中的时序参数
通过前一篇文章学习,我们可以大致知道内存条(Module)的组成及SDRAM内部的结构,这一篇再介绍下SDRAM中常见的时序参数以及整个读写操作的流程。 一、外部信号 图1 DDR4的外部线路图 DDR是一种高带宽的传输接口,其外部信号较多,图1是一个DDR4的外部线路图,以下对图中跟通…...

语义分割 - 简介
语义分割是计算机视觉领域的一项重要任务,旨在将图像中的每个像素标记为对应的语义类别。与传统的图像分类任务不同,语义分割不仅要识别整个图像的类别,还需要对图像中的每个像素进行分类,从而实现对图像的像素级别理解。 语义分…...

ch0_OSI 七层网络协议介绍
目录 概述 1、三网融合的概念 三网:电信网络、有线电视网络、计算机网络 概念:把上述三种网络融合成一种网络 2、计算机网络的定义、分类 定义:计算机网络是将地理位置不同的独立计算机系统,通过传输介质链接起来,…...

超声波俱乐部分享:百度世界大会点燃AI创业者新希望
10月22日,2023年第十三期超声波俱乐部内部分享会在北京望京举行。本期的主题是:百度世界大会点燃AI创业者新希望。 到场的嘉宾有:超声波创始人杨子超,超声波联合创始人、和牛商业创始人刘思雨,中国国际经济交流中心研…...

【项目管理】项目计划中常见影响进度的风险汇总
哈喽,大家好,我是雷工。 在项目实施过程中针对项目进度的计划常常会有各种各样的的风险,相比出了问题去救火与填坑,能够提前预知风险,并提前调整计划,更能有利于项目的如期交付。 以下为项目计划中影响进度…...

Apache HttpClient库编写的Scala程序
Apache HttpClient库编写的Scala下载器程序,用于下载图片。代码如下: import org.apache.http.HttpHost import org.apache.http.client.HttpClients import org.apache.http.client.methods.HttpHead import org.apache.http.impl.client.CloseableHtt…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...

Spring Boot + MyBatis 集成支付宝支付流程
Spring Boot MyBatis 集成支付宝支付流程 核心流程 商户系统生成订单调用支付宝创建预支付订单用户跳转支付宝完成支付支付宝异步通知支付结果商户处理支付结果更新订单状态支付宝同步跳转回商户页面 代码实现示例(电脑网站支付) 1. 添加依赖 <!…...
