代码随想录算法训练营第10天|232. 用栈实现队列 225. 用队列实现栈
JAVA代码编写
232. 用栈实现队列
请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty):
实现 MyQueue 类:
void push(int x)将元素 x 推到队列的末尾int pop()从队列的开头移除并返回元素int peek()返回队列开头的元素boolean empty()如果队列为空,返回true;否则,返回false
说明:
- 你 只能 使用标准的栈操作 —— 也就是只有
push to top,peek/pop from top,size, 和is empty操作是合法的。 - 你所使用的语言也许不支持栈。你可以使用 list 或者 deque(双端队列)来模拟一个栈,只要是标准的栈操作即可。
示例 1:
输入:
["MyQueue", "push", "push", "peek", "pop", "empty"]
[[], [1], [2], [], [], []]
输出:
[null, null, null, 1, 1, false]解释:
MyQueue myQueue = new MyQueue();
myQueue.push(1); // queue is: [1]
myQueue.push(2); // queue is: [1, 2] (leftmost is front of the queue)
myQueue.peek(); // return 1
myQueue.pop(); // return 1, queue is [2]
myQueue.empty(); // return false
提示:
1 <= x <= 9- 最多调用
100次push、pop、peek和empty - 假设所有操作都是有效的 (例如,一个空的队列不会调用
pop或者peek操作)
进阶:
- 你能否实现每个操作均摊时间复杂度为
O(1)的队列?换句话说,执行n个操作的总时间复杂度为O(n),即使其中一个操作可能花费较长时间。
教程:https://programmercarl.com/0232.%E7%94%A8%E6%A0%88%E5%AE%9E%E7%8E%B0%E9%98%9F%E5%88%97.html#%E7%AE%97%E6%B3%95%E5%85%AC%E5%BC%80%E8%AF%BE
解:
思路:队列由两个栈表示:进栈stackIn、出栈stackOut
-
队列进队push:等价于直接进栈
-
队列出队pop:将stackIn中出栈到stackOut中,然后再出栈
- dumpstackIn()函数:将stackIn中出栈到stackOut中
-
返回队列底元素(最先入队的元素):相当岁返回stackOut的栈顶元素
-
队列是否为空:为空的话,就是要stackIn和stackOut都为空
import java.util.Stack;class MyQueue {Stack<Integer> stackIn;Stack<Integer> stackOut;/** Initialize your data structure here. */public MyQueue() {stackIn = new Stack<>(); // 负责进栈stackOut = new Stack<>(); // 负责出栈}/** Push element x to the back of queue.入队 */public void push(int x) {stackIn.push(x);}/** Removes the element from in front of queue and returns that element. 删除该队列元素,删第一个进队列的*/public int pop() {dumpstackIn();return stackOut.pop();}/** Get the front element. 返回队列底元素:最先入队的元素*/public int peek() {dumpstackIn();return stackOut.peek();}/** Returns whether the queue is empty. */public boolean empty() {return stackIn.isEmpty() && stackOut.isEmpty();}// 如果stackOut为空,那么将stackIn中的元素全部放到stackOut中private void dumpstackIn(){if (!stackOut.isEmpty()) return;while (!stackIn.isEmpty()){stackOut.push(stackIn.pop());}}public static void main(String[] args) {MyQueue myQueue= new MyQueue();myQueue.push(1);myQueue.push(2);myQueue.push(3);myQueue.push(4);myQueue.pop();myQueue.push(5);myQueue.push(6);System.out.println(myQueue.peek());}
}225. 用队列实现栈
请你仅使用两个队列实现一个后入先出(LIFO)的栈,并支持普通栈的全部四种操作(push、top、pop 和 empty)。
实现 MyStack 类:
void push(int x)将元素 x 压入栈顶。int pop()移除并返回栈顶元素。int top()返回栈顶元素。boolean empty()如果栈是空的,返回true;否则,返回false。
注意:
- 你只能使用队列的基本操作 —— 也就是
push to back、peek/pop from front、size和is empty这些操作。 - 你所使用的语言也许不支持队列。 你可以使用 list (列表)或者 deque(双端队列)来模拟一个队列 , 只要是标准的队列操作即可。
示例:
输入:
["MyStack", "push", "push", "top", "pop", "empty"]
[[], [1], [2], [], [], []]
输出:
[null, null, null, 2, 2, false]解释:
MyStack myStack = new MyStack();
myStack.push(1);
myStack.push(2);
myStack.top(); // 返回 2
myStack.pop(); // 返回 2
myStack.empty(); // 返回 False
提示:
1 <= x <= 9- 最多调用
100次push、pop、top和empty - 每次调用
pop和top都保证栈不为空
**进阶:**你能否仅用一个队列来实现栈。
教程:https://programmercarl.com/0225.%E7%94%A8%E9%98%9F%E5%88%97%E5%AE%9E%E7%8E%B0%E6%A0%88.html
解:
思路:栈由两个队列表示:queue1、queue2
- 进栈push:将元素,进队到queue2;当queue1不是空的时候,将queue1出队的元素入队到queue2;再交换queue1和queue2
import java.util.LinkedList;
import java.util.Queue;class MyStack {Queue<Integer> queue1; // 和栈中保持一样元素的队列Queue<Integer> queue2; // 辅助队列/** Initialize your data structure here. */public MyStack() {queue1 = new LinkedList<>();queue2 = new LinkedList<>();}/** Push element x onto stack. 入栈*/public void push(int x) {queue2.offer(x); // 先放在辅助队列中,offer:元素入队while (!queue1.isEmpty()){queue2.offer(queue1.poll());//poll:移除并返回队列头部的元素//逆序存入queue2}Queue<Integer> queueTemp;queueTemp = queue1;queue1 = queue2;queue2 = queueTemp; // 最后交换queue1和queue2,将元素都放到queue1中}/** Removes the element on top of the stack and returns that element. */public int pop() {return queue1.poll(); // 因为queue1中的元素和栈中的保持一致,所以这个和下面两个的操作只看queue1即可}/** Get the top element. */public int top() {return queue1.peek();}/** Returns whether the stack is empty. */public boolean empty() {return queue1.isEmpty();}public static void main(String[] args) {MyStack myStack = new MyStack();myStack.push(1);myStack.push(2);myStack.push(3);myStack.pop();myStack.push(4);}
}
相关文章:

代码随想录算法训练营第10天|232. 用栈实现队列 225. 用队列实现栈
JAVA代码编写 232. 用栈实现队列 请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty): 实现 MyQueue 类: void push(int x) 将元素 x 推到队列的末尾int pop() 从队列的开头移除…...

线上Kafka集群如何调整消息存储时间
这里是weihubeats,觉得文章不错可以关注公众号小奏技术,文章首发。拒绝营销号,拒绝标题党 Kafka版本 kafka_2.13-3.5.0 背景 Kafka 默认消息存储时间为7天,实际线上的业务使用Kafka更多的是一些数据统计之类的业务,大多是朝生夕…...
[迁移学习]DA-DETR基于信息融合的自适应检测模型
原文标题为:DA-DETR: Domain Adaptive Detection Transformer with Information Fusion;发表于CVPR2023 一、概述 本文所描述的模型基于DETR,DETR网络是一种基于Transformer的目标检测网络,详细原理可以参见往期文章:…...
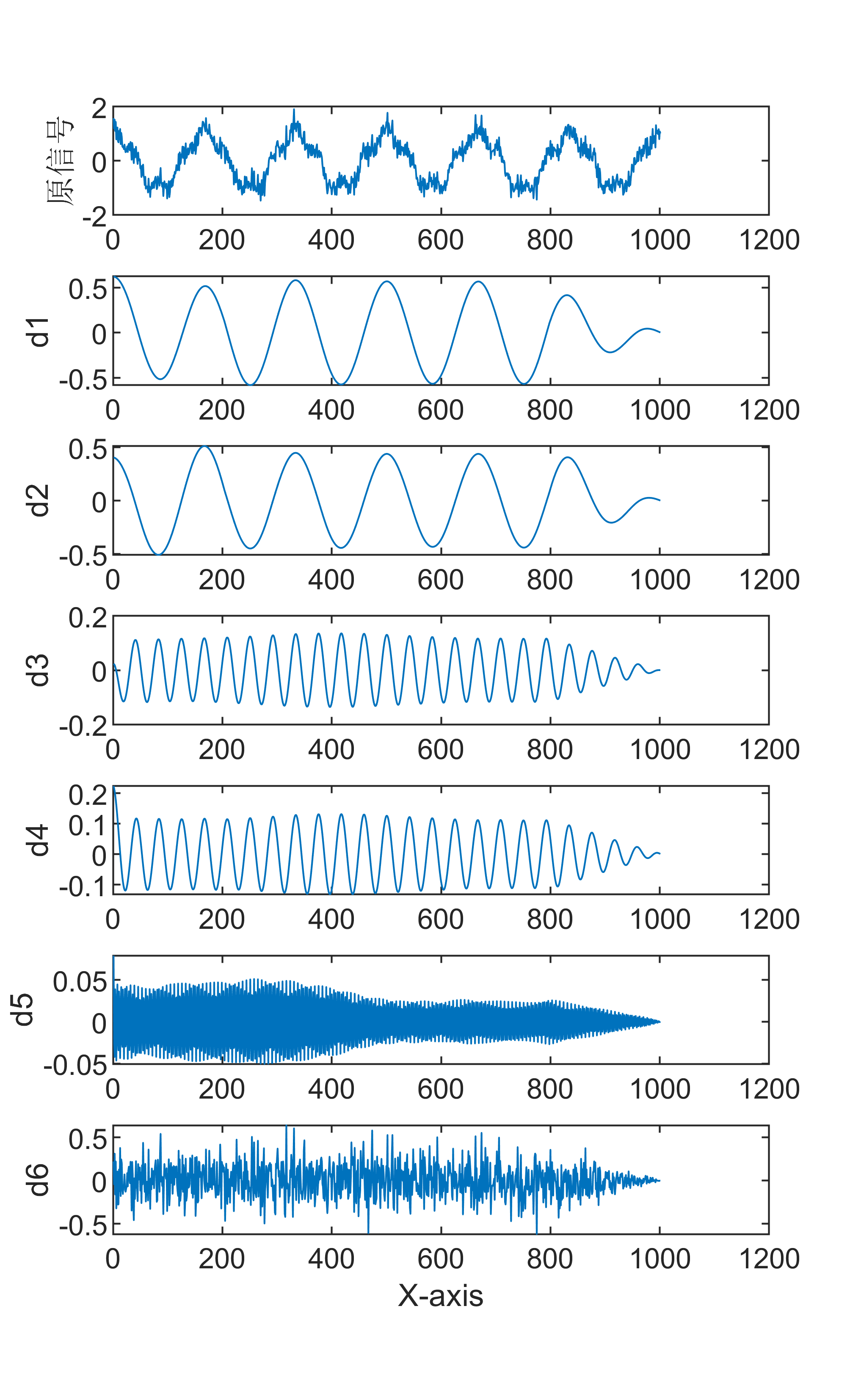
【MATLAB】全网唯一的13种信号分解+FFT傅里叶频谱变换联合算法全家桶
有意向获取代码,请转文末观看代码获取方式~ 大家吃一顿火锅的价格便可以拥有13种信号分解FFT傅里叶频谱变换联合算法,绝对不亏,知识付费是现今时代的趋势,而且都是我精心制作的教程,有问题可随时反馈~也可单独获取某一…...
Nginx安装与配置
1.下载安装包 官网下载地址:nginx: download 可以先将安装包下载到本地再传到服务器,或者直接用wget命令将安装包下载到服务器,这里我们直接将安装包下载到服务器上。未安装wget命令的需要先安装wget,yum install -y wget [root…...

linux笔记总结-基本命令
参考: 1.Linux 和Windows比 比较 (了解) 1. 记住一句经典的话:在 Linux 世界里,一切皆文件 2. Linux目录结构 /lib • 系统开机所需要最基本的动态连接共享库,其作用类似于Windows里的DLL文件。几 乎所有…...
[PHP]禅道项目管理软件ZenTaoPMS源码包 v16.4
禅道项目管理软件ZenTaoPMS一键安装包是一款国产的开源项目管理软件。它集产品管理、项目管理、质量管理、文档管理、组织管理和事务管理于一体,是一款专业的研发项目管理软件,完整地覆盖了项目管理的核心流程。注重实效的管理思想,合理的软件…...

Required String parameter ‘name‘ is not present
[org.springframework.web.bind.MissingServletRequestParameterException: Required String parameter name is not present] 服务端有参数name,客户端没有传上来...
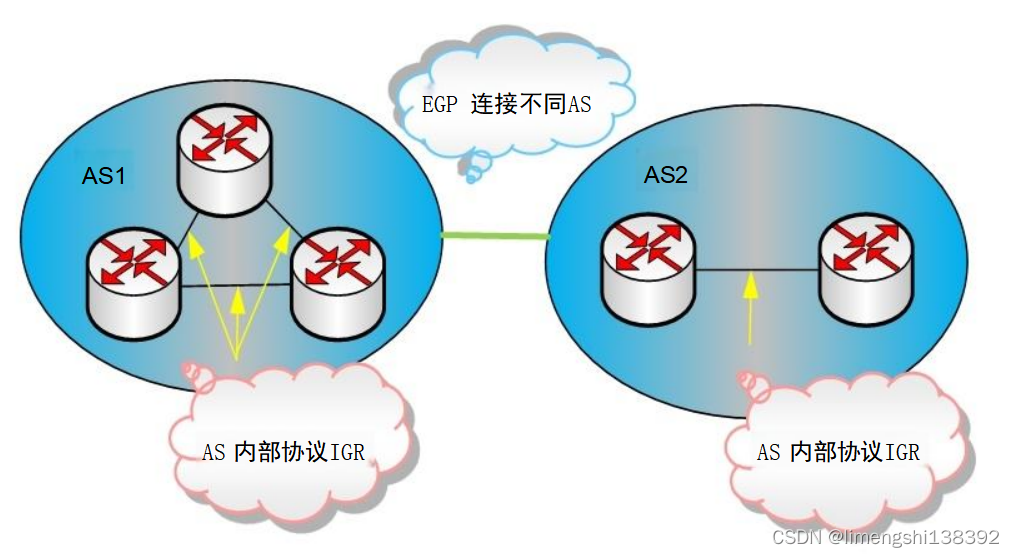
路由器基础(五): OSPF原理与配置
开放式最短路径优先 (Open Shortest Path First,OSPF) 是一个内部网关协议 (Interior Gateway Protocol,IGP),用于在单一自治系统(Autonomous System,AS) 内决策路由。OSPF 适合小型、中型、较大规模网络。OSPF 采用Dijkstra的最短路径优先算法 (Shortest Pat…...
Leetcode1128. 等价多米诺骨牌对的数量
Every day a Leetcode 题目来源:1128. 等价多米诺骨牌对的数量 解法1:暴力 代码: class Solution { public:int numEquivDominoPairs(vector<vector<int>> &dominoes){int n dominoes.size(), count 0;for (int i 0;…...
Dev-C调试的基本方法2-2
3.3 跳出函数 在图6所示的状态下,点击单步调试(F7)会继续调试下一行,而如果想结束在函数中的调试,则点击图4③所示的跳出函数,或CtrlF8按键跳出f()函数,程序将会停在图5所示的第11行处。 3.4 …...

企业之间的竞争,ISO三体系认证至关重要!
ISO三体系认证是指ISO 9001质量管理体系认证、ISO 14001环境管理体系认证、ISO 45001(OHSAS18001)职业健康安全管理体系认证。企业(组织)自愿申请、通过ISO三体系认证,并贯彻落实,确实能获益多多。 ISO 9001质量管理体系 我们经…...
node教程(四)Mongodb+mongoose
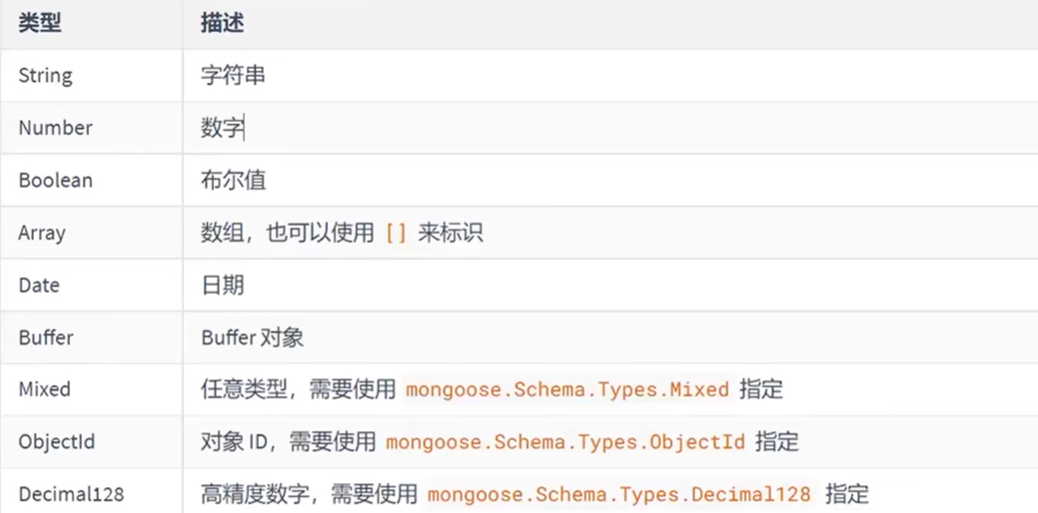
文章目录 一、mongodb1.简介1.1Mongodb是什么?1.2数据库是什么?1.3数据库的作用1.4数据库管理数据的特点 2.核心概念3.下载安装与启动4.命令行交互4.1数据库命令4.3文档命令 二、Mongoose1.介绍2.作用3.使用流程4.插入文档5.mongoose字段类型 一、mongod…...

作为一个初学者,该如何入门大模型?
在生成式 AI 盛行的当下,你是否被这种技术所折服,例如输入一段简简单单的文字,转眼之间,一幅精美的图片,又或者是文笔流畅的文字就展现在你的面前。 相信很多人有这种想法,认为生成式 AI 深不可测…...

编译支持GPU的opencv,并供python的import cv2调用
下载opencv和opencv_contrib,cmake过程中要下载的一些包可以手动下载配置,如果网络较好,也可以等待自动下载。主要记录的是cmake命令: cmake -D CMAKE_BUILD_TYPERELEASE \-D BUILD_opencv_python3YES \-D CMAKE_INSTALL_PREFIX/…...

Bug记录
那些年写过的很小的bug: Bug1: if args.model IRNN or irnn:# some code这实际上不会按你期望的方式工作。原因在于 ‘irnn’ 是一个非空的字符串,因此它在布尔上下文中被视为 True。所以条件总是为真,而不会考虑 args.model 的…...
web3 React dapp中编写balance组件从redux取出并展示用户资产
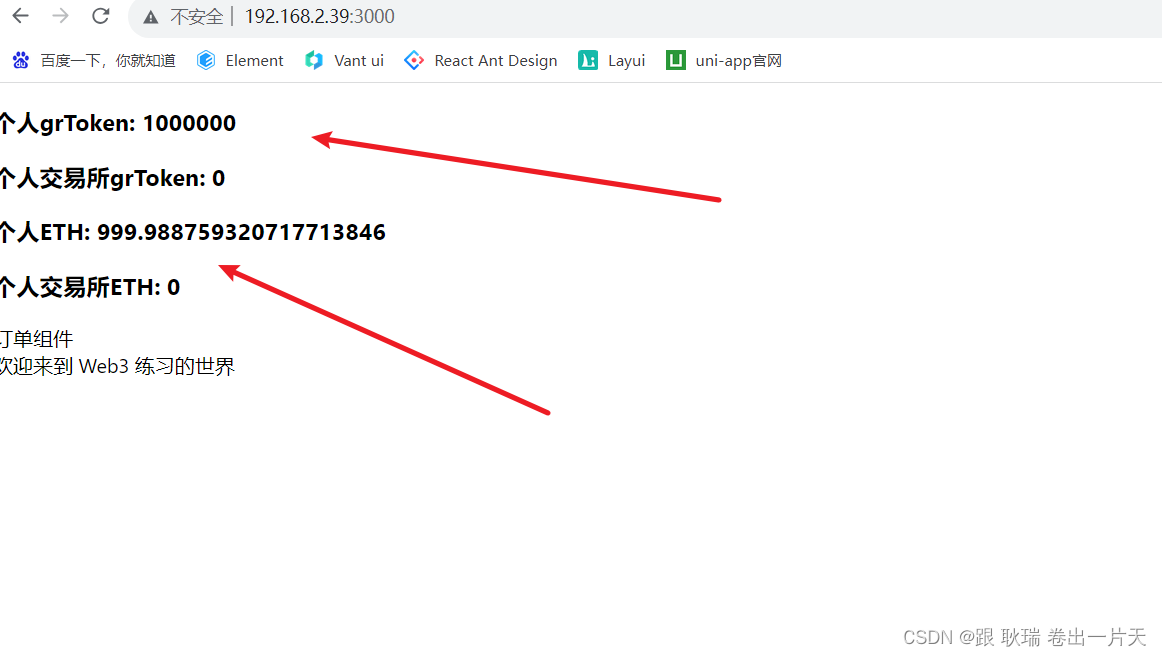
好啊 上文WEB3 在 React搭建的Dapp中通过redux全局获取并存储用户ETH与自定义token与交易所存储数量中 我们拿到了用户的一个本身 和 交易所token数量 并放进了redux中做了一个全局管理 然后 我们继续 先 起来ganache的一个模拟环境 ganache -d然后 我们启动自己的项目 顺手发…...
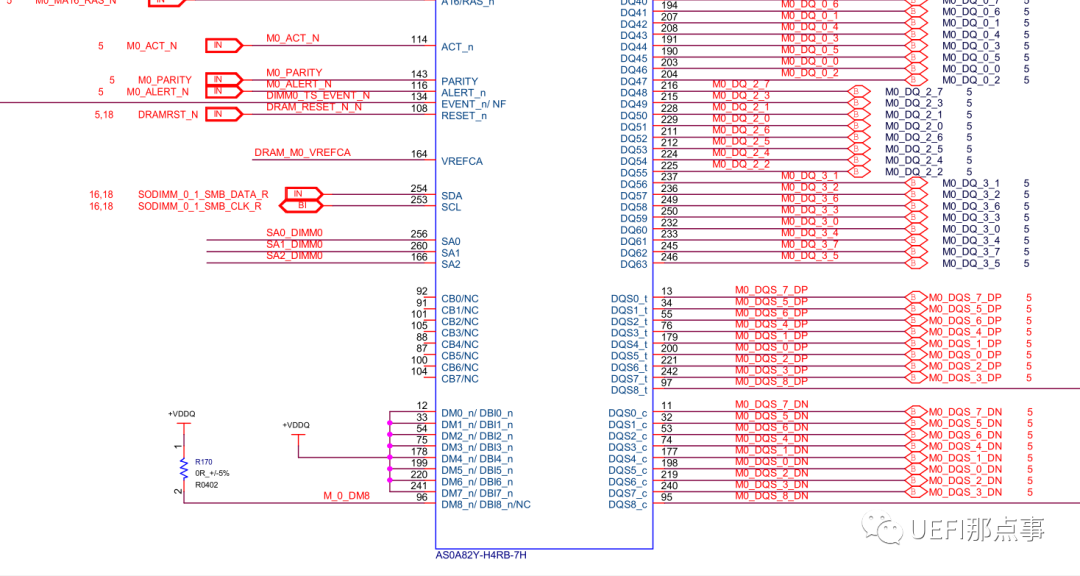
BIOS开发笔记 - DDR中的时序参数
通过前一篇文章学习,我们可以大致知道内存条(Module)的组成及SDRAM内部的结构,这一篇再介绍下SDRAM中常见的时序参数以及整个读写操作的流程。 一、外部信号 图1 DDR4的外部线路图 DDR是一种高带宽的传输接口,其外部信号较多,图1是一个DDR4的外部线路图,以下对图中跟通…...

语义分割 - 简介
语义分割是计算机视觉领域的一项重要任务,旨在将图像中的每个像素标记为对应的语义类别。与传统的图像分类任务不同,语义分割不仅要识别整个图像的类别,还需要对图像中的每个像素进行分类,从而实现对图像的像素级别理解。 语义分…...

ch0_OSI 七层网络协议介绍
目录 概述 1、三网融合的概念 三网:电信网络、有线电视网络、计算机网络 概念:把上述三种网络融合成一种网络 2、计算机网络的定义、分类 定义:计算机网络是将地理位置不同的独立计算机系统,通过传输介质链接起来,…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...
