代碼隨想錄算法訓練營|第五十九天|647. 回文子串、7516.最长回文子序列、动态规划总结篇。刷题心得(c++)
目录
讀題
647. 回文子串
看完代码随想录之后的想法
516.最长回文子序列
看完代码随想录之后的想法
647. 回文子串 - 實作
思路
動態規劃思路
雙指針思路
Code
動態規劃思路
雙指針思路
516.最长回文子序列 - 實作
思路
Code
动态规划 - 總結
動態規劃基礎
動態規劃五部曲
誤區
動態規劃與貪心算法的差別
靈魂三問
基礎題目
背包問題
背包問題 - 遞推公式
遍歷順序差異
打家劫舍
股票問題
子序列問題
編輯距離問題
回文子串問題
讀題
647. 回文子串
看完代码随想录之后的想法
對於dp數組的定義又有了進一步的了解,之前沒有想到可以使用i,j這兩個下標來表示範圍,理解過後使用上就比較知道怎做了,並且後續也有談到如何使用雙指針法進行,基本上就是利用回文子串的特性,相對的位置上一定相同,在這題上又加深了自己對於雙指針以及回文特性的操作。
516.最长回文子序列
看完代码随想录之后的想法
原本有想到應該是類似於647,但自己只有想清楚了下標,但沒有想清楚遞推公式,看題解之前並沒有去思考說相等等於原本的回文子串+2長度,並且不相等時當時想過很多,但後面看完之後才知道是去取兩段範圍內最長的部分,在這個題目當中又複習到了之前的操作。
647. 回文子串 - 實作
思路
動態規劃思路
<aside> 💡 根據字符串的性質決定dp數組的定義
</aside>
-
定義DP數組以及下標的含意
dp[i][j]: [i, j]範圍內的字符串是否為回文子串
-
遞推公式
dp[i][j] s[i] s[j] 相等有三種狀況
-
兩者指向同一個元素,範圍為0,j - i = 0;
-
兩者相差一個元素,即相鄰,範圍為1,j - i = 1;
-
兩者相差大於一個元素,其實可以想成兩者範圍內的元素是否為回文子串,如下圖
如果[i+2, j-2] [i+1][j-1]都是回文子串,那當s[i]s[j]相等時,一定也會是回文子串
|------|------|------|------| i i+1 i+2 j-1 jj-2
-
-
根據遞推公式、題意以及定義,確定DP數組如何初始化
將dp數組都初始化為false,確保每一次的狀態都是由自己推的
-
確定遍歷順序
可以看到dp[i][j]是由左下角的值推導出來的,所以遍歷順序應該是由下到上由左到右。
+------------+------------+ | | dp[i][j] | +------------+------------+ |dp[i+1][j-1]| | +------------+------------+
雙指針思路
<aside> 💡 雙指針法,由中間往外擴散出去,進行遍歷
</aside>
-
定義函數,
來遍歷以i,j為中心的數組,往左右擴散並確認是否為回文字串
需要傳入的參數
i,j,左邊界以及字串
回傳以i、j為中心的的回文字串有多少個。
-
主函數
有兩種狀況,i以及i與i+1,因為中心點有可能是一個數也有可能是兩個數
遍歷字符串所有位置
定義一個result變數紀錄回文字串的總數
Code
動態規劃思路
class Solution {
public:int countSubstrings(string s) {vector<vector<bool>> dp (s.size(), vector<bool>(s.size(), false));int result = 0;for(int i = s.size() - 1; i >= 0; i--) {for(int j = i; j < s.size(); j++) {if(s[i] == s[j]) {if(j - i <= 1) {dp[i][j] = true;result++;} else if(dp[i + 1][j - 1] == true) {dp[i][j] = true;result++;}}}}return result;}
};
雙指針思路
class Solution {
public:int countSubstrings(string s) {int result = 0;for(int i = 0; i < s.size(); i++) {result += extend(s, i, i, s.size());result += extend(s, i, i + 1, s.size());}return result;}int extend(string& s, int i, int j, int n) {int res = 0;while(i >= 0 && j < n && s[i] == s[j]) {i--;j++;res++;}return res;}
};
516.最长回文子序列 - 實作
思路
<aside> 💡 根據字符串的性質決定dp數組的定義
</aside>
-
定義DP數組以及下標的含意
dp[i][j]: [i, j]範圍內的字符串最長回文子串長度為dp[i][j]
-
遞推公式
相等: s[i] s[j] 相等代表說這兩個數值可以加入到回文子串最長的範圍內,所以是dp[i + 1][j - 1] + 2,代表上
|------|------|------|------| i i+1 i+2 j-1 jj-2不相等: s[i] s[j] 不相等代表說這兩個數值無法到回文子串最長的範圍內,所以我們要找出上一次i ~ j - 1 以及i + 1 ~ j的這兩個範圍內,誰有最長的回文子串。
所以是max(dp[i+1][j], dp[i][j - 1]) 範圍內哪段回文子串最長。
|--------------------| i j-1|--------------------|i+1 j |------|------|------|------| i i+1 i+2 j-1 jj-2兩者指向同一個元素,範圍為0,j - i = 0;
-
兩者相差一個元素,即相鄰,範圍為1,j - i = 1;
-
兩者相差大於一個元素,其實可以想成兩者範圍內的元素是否為回文子串,如下圖
如果[i+2, j-2] [i+1][j-1]都是回文子串,那當s[i]s[j]相等時,一定也會是回文子串
-
-
根據遞推公式、題意以及定義,確定DP數組如何初始化
在i跟j 相同時,可以知道最長回文子串的長度都是1,而在遞推公式中是計算不到i、j相同的情況。
將dp數組都初始化為0,並確保i、j相等的狀態都是1。
-
確定遍歷順序
可以看到dp[i][j]是由左下角的值推導出來的,所以遍歷順序應該是由下到上由左到右。
+------------+------------+ | dp[i][j-1] | dp[i][j] | +------------+------------+ |dp[i+1][j-1]| dp[i+1][j] | +------------+------------+
Code
class Solution {
public:int longestPalindromeSubseq(string s) {vector<vector<int>> dp (s.size(), vector<int>(s.size(), 0));for(int i = 0; i < s.size(); i++) dp[i][i] = 1;for(int i = s.size() - 1; i >= 0; i--) {for(int j = i + 1; j < s.size(); j++) {if(s[i] == s[j]) {dp[i][j] = dp[i + 1][j - 1] + 2;} else {dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);}}}return dp[0][s.size() - 1];}
};
动态规划 - 總結
動態規劃基礎
動態規劃五部曲
-
定義DP數組以及下標的含意
如果想不清楚dp数组的具体含义,递归公式从何谈起,甚至初始化的时候就写错了。
dp[i][j] i 代表甚麼意思,j代表甚麼意思
dp[i] i 代表甚麼意思,元素代表甚麼意思
-
遞推公式
-
根據遞推公式,確定DP數組如何初始化
例如**动态规划:不同路径还不够,要有障碍! (opens new window)**在这道题目中,初始化才是重头戏
-
確定遍歷順序
如果看过背包系列,特别是完全背包,那么两层for循环先后顺序绝对可以搞懵很多人,反而递归公式是简单的。
-
打印dp數組
至于推导dp数组的重要性,动规专题里几乎每篇Carl都反复强调,当程序结果不对的时候,一定要自己推导公式,看看和程序打印的日志是否一样。
誤區
遞推公式不該是過於關注的點,它只是解題的一部分,別讓自己在解題時處於黑盒狀態
動態規劃與貪心算法的差別
動態規劃每一個狀態一定是由上一個狀態推導出來,而貪心則是從局部選最優堆疊成全局最優
靈魂三問
- 这道题目我举例推导状态转移公式了么?
- 我打印dp数组的日志了么?
- 打印出来了dp数组和我想的一样么?
基礎題目
- 动态规划:斐波那契数(opens new window)
- 动态规划:爬楼梯(opens new window)
- 动态规划:使用最小花费爬楼梯(opens new window)
- 动态规划:不同路径(opens new window)
- 动态规划:不同路径还不够,要有障碍!(opens new window)
- 动态规划:整数拆分,你要怎么拆?(opens new window)
- 动态规划:不同的二叉搜索树
背包問題
背包問題 - 遞推公式
-
最多裝多少/能否裝滿
dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]); → 可以想像成物品重量與價值相等
對應題目
- 动态规划:416.分割等和子集(opens new window)
- 动态规划:1049.最后一块石头的重量 II
-
最大價值
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); → 可以想像成物品重量與價值不相等
對應題目
- 动态规划:474.一和零
-
裝滿背包有多少方式
dp[j] += dp[j - nums[i]];
對應題目
- 动态规划:494.目标和(opens new window)
- 动态规划:518. 零钱兑换 II(opens new window)
- 动态规划:377.组合总和Ⅳ(opens new window)
- 动态规划:70. 爬楼梯进阶版(完全背包)
-
最少裝多少/能否裝滿
dp[j] = min(dp[j - coins[i]] + 1, dp[j])
對應題目
- 动态规划:322.零钱兑换(opens new window)
- 动态规划:279.完全平方数
遍歷順序差異
-
01背包
-
二維dp
因為數值都會根據左上方以及正上方的值進行更新,所以當我們初始化第一行與第一列時,不管是從背包開始遞推還是物品開始遞推,都可以。
第二層遍歷順序是由小到大
-
一維dp
在二维數組中,每一層的數值都是當前位置的正上方以及左上方的數據得出
從二维壓縮成一维數組,我們需要模擬二维數組的方式
所以根據我們的遞推公式,我們不能使用正序遍歷,不然原本在二维數組中左上方的數據就會被覆蓋掉
而使用倒序可以保證每一層的數據都是由二维數組上一層正上方以及左上方得出的。
-
二維dp 滾動dp
在**动态规划:474.一和零 中是有兩個維度的背包**
先遍歷物品,在遍歷二維背包
因為是滾動數組,所以二維背包是由後往前遍歷
-
-
完全背包
在純完全背包的問題當中,既然物品可以被選取無限次,那麼考慮某個物品時不必限制只看一次。
換句話說,可以在考慮這個物品的同時也考慮其他所有的物品。
因此,不論先遍歷物品還是先遍歷容量,結果都是一樣的。
如果求最小数,那么两层for循环的先后顺序就无所谓了,相关题目如下:
- 求最小数:动态规划:322. 零钱兑换 (opens new window)、动态规划:279.完全平方数
但如果題目要求的回答是組合或者是排序就會有所差別
組合 - 不要求順序性: 外層遍歷物品內層遍歷背包
排列- 要求順序性: 外層遍歷背包內層遍歷物品
相關題目
- 求组合数:动态规划:518.零钱兑换II(opens new window)
- 求排列数:动态规划:377. 组合总和 Ⅳ (opens new window)、动态规划:70. 爬楼梯进阶版(完全背包)
可以想像在求組合的時候,外層遍歷物品,確保每個背包至多只會有一次的組合
但在求排序時,因為每個背包都會重新遍歷物品,所以會有不同的順序被計算到
打家劫舍
- 對應問題
- 动态规划:开始打家劫舍!(opens new window)
- 动态规划:继续打家劫舍!(opens new window)
- 动态规划:还要打家劫舍!
股票問題
-
單一股票買賣一次求最大数值,主要就是定義上持有股票的現金以及不持有的部分進行初步的劃分
-
动态规划:121.买卖股票的最佳时机
-
透過遞規公式找出数組中的最大数值
dp[i][0] = max(dp[i - 1][0], -prices[i]); dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i]);
-
-
單一股票買賣多次求最大数值,主要就是定義上持有股票的現金以及不持有的部分進行初步的劃分
-
动态规划:122.买卖股票的最佳时机II
-
在遞推公式上就是在買入的時機會出現差異,變成是說上一次獲得的現金,減去當下的股票金額,哪個優
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]); dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i]);
-
-
單一股票只能買賣特定次数
-
动态规划:123.买卖股票的最佳时机III 、 动态规划:188.买卖股票的最佳时机IV
-
主要體現在下標上面就會有差異,分為沒有操作、買入股票、賣出股票這三個部分
-
因為每次的買賣都一定是2 * k 次(買入、賣出),所以在的推公式上其實就是將買賣次数進行抽象化處理
for(int j = 1; j < 2 * k + 1; j++) {if(j % 2 == 1) dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - 1] - prices[i]);else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - 1] + prices[i]); }
-
-
單一股票只能買賣包含冷凍期
-
动态规划:309.最佳买卖股票时机含冷冻期
-
主要體現在定義上會有所差別,需要將賣出的狀態分為,保持賣出以及賣出,這樣使得冷凍期的數值有所依歸
-
遞推公式如下
dp[i][0] = max(dp[i - 1][0], max(dp[i - 1][3]- prices[i], dp[i - 1][1]- prices[i])); dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]); dp[i][2] = dp[i - 1][0] + prices[i]; dp[i][3] = dp[i - 1][2];
-
-
單一股票多次買賣包含手續費
-
动态规划:714.买卖股票的最佳时机含手续费
-
主要體賣出時,需要多加上一個手續費的計算
-
遞推公式如下
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]); dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i] - fee);
-
子序列問題
編輯距離問題
在編輯距離的題目當中,有個很重要的核心就是定義好dp[i][j]的定義,在根據這個定義,去推導出公式以及初始化的方式
其實前三題很重要的思維就是對於刪除的理解,在不同的定義上刪除的做法都不太一樣
- 判斷子序列
刪除是dp[i][j - 1],忽略前一個t
- 不同子序列
使用s[i - 1]的,我不用刪除任何元素,所以值會是dp[i - 1][j - 1]即上一次的狀況,
如果不使用s[i - 1]的狀況,我等同於只需要不考慮s[i - 1] 但t[j - 1]仍然在,所以值會是dp[i - 1][j]
相同時的轉移方程就會是dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
兩者不相等時相當於s 要刪除元素,因為 s的字符串中,這個位置並沒有t的字串,所以要刪除
如果是s要刪除元素,那就是取s[i - 2] 這個不包含s[ i -1]的最大值,但t是要比較的子序列,所以t不用動,也就是說這個dp[i][j]會是由s[i - 2]t[j - 1]所組成,所對應的dp數組是dp[i][j] = dp[i - 1][j]。
-
兩個字符串的刪除操作
- 刪除word1
- 代表不包含當前word1的狀況在加上一個刪除的個數也就是dp[i - 1][j] + 1
- 刪除word2
- 代表不包含當前word2的狀況再加上1個刪除數,也就是dp[i][j - 1] + 1
- 刪除word1、word2
- 代表要不包含word1以及word2的值,也就是dp[i - 1][j - 1] ,並加上刪除兩次,所以是dp[i - 1][j - 1] + 2
- 刪除word1
-
編輯距離
所謂的增刪基本上是同一個操作數,只是需要明確甚麼是替換,以及下標定義為何
- 需要增刪word1時,都是取dp[i - 1][j] + 1
- 需要增刪word2時,都是取dp[i][j - 1] + 1
- 需要替換word1或word2的話,則需要取這兩個都不存在的部分加上一次操作數也就是dp[i - 1][j - 1] + 1
-
對應題目
- 动态规划:最长递增子序列(opens new window)
- 动态规划:最长连续递增序列(opens new window)
- 动态规划:最长重复子数组(opens new window)
- 动态规划:最长公共子序列(opens new window)
- 动态规划:不相交的线(opens new window)
- 动态规划:最大子序和(opens new window)
- 动态规划:判断子序列(opens new window)
- 动态规划:不同的子序列(opens new window)
- 动态规划:两个字符串的删除操作(opens new window)
- 动态规划:编辑距离
回文子串問題
<aside> 💡 根據字符串的性質決定dp數組的定義
</aside>
主要就是對於回文子串的性質要清晰,並且dp數組定義時要定義清楚
- 對應題目
- 动态规划:回文子串(opens new window)
- 动态规划:最长回文子序列
相关文章:
)
代碼隨想錄算法訓練營|第五十九天|647. 回文子串、7516.最长回文子序列、动态规划总结篇。刷题心得(c++)
目录 讀題 647. 回文子串 看完代码随想录之后的想法 516.最长回文子序列 看完代码随想录之后的想法 647. 回文子串 - 實作 思路 動態規劃思路 雙指針思路 Code 動態規劃思路 雙指針思路 516.最长回文子序列 - 實作 思路 Code 动态规划 - 總結 動態規劃基礎 動…...

Qt封装的Halcon显示控件,支持ROI绘制
前言 目前机器视觉ROI交互控件在C#上做的比较多,而Qt上做的比较少,根据作者 VSQtHalcon——显示图片,实现鼠标缩放、移动图片的文章,我在显示和移动控件的基础上,增加了ROI设置功能,并封装成了一个独立的Q…...
基于深度学的图像修复 图像补全 计算机竞赛
1 前言 🔥 优质竞赛项目系列,今天要分享的是 基于深度学的图像修复 图像补全 该项目较为新颖,适合作为竞赛课题方向,学长非常推荐! 🧿 更多资料, 项目分享: https://gitee.com/dancheng-se…...

vue3框架全局修改样式(字体颜色以及初始化定义基础elemplent颜色)
问题1、全局修改vue管理系统框架的字体颜色(index.scss目录下修改) 问题2、vue3中使用elemplent-plus中的el-select组件,默认选中二级或三级的一个数据,没有显示label只显示了id 问题如下 原因是因为 这个属性为true了࿰…...

Linux - 进程控制(上篇)- 进程创建 和 进程终止
进程控制 进程创建 对于进程的创建,你肯定知道,在 C/C 当中使用 fork()函数,以当前可执行程序生成的进程为 父进程,创建这个父进程的 一个子进程,这个 子进程就是一个新的进程。 如上图所示&a…...

NiceGui:Python中的轻量级GUI框架初体验
目录 一、引言 二、NiceGui概述 三、NiceGui实战:一个简单的计算器应用 四、NiceGui与其他GUI框架的比较 五、注意事项 总结与展望 一、引言 Python作为一门功能强大且易于学习的编程语言,广泛应用于各种领域。在图形用户界面(GUI&…...

php 常用的接口和函数
ArrayAccess — interface to provide accessing to objects as arrays 提供以数组形式访问对象的接口。 interface synopsis 接口需要实现下面几个方法 interface ArrayAccess { /* Methods */ public offsetExists(mixed $offset): bool public offsetGet(mixed $offset):…...
:掌握 AnimatedBuilder 将动画的逻辑和 UI 代码分离)
【Flutter】Flutter 动画深入解析(2):掌握 AnimatedBuilder 将动画的逻辑和 UI 代码分离
【Flutter】Flutter 动画深入解析(2):掌握 AnimatedBuilder 将动画的逻辑和 UI 代码分离 文章目录 一、前言二、Flutter 动画简介三、什么是 AnimatedBuilder四、AnimatedBuilder 与其他动画小部件的比较五、如何使用 AnimatedBuilder六、实际业务中的应用场景七、完整示例八…...

Spring Boot中解决跨域问题(CORS)
1. 跨域介绍 首先解释什么是跨域,跨域就是前端和后端的端口号不同;会产生跨域问题,这里浏览器的保护机制(同源策略)。 同源策略:前端和后端的协议、域名、端口号三者都相同叫做同源。 我们看一下不同源&am…...

基于生成对抗网络的照片上色动态算法设计与实现 - 深度学习 opencv python 计算机竞赛
文章目录 1 前言1 课题背景2 GAN(生成对抗网络)2.1 简介2.2 基本原理 3 DeOldify 框架4 First Order Motion Model5 最后 1 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 基于生成对抗网络的照片上色动态算法设计与实现 该项目较为新颖&am…...
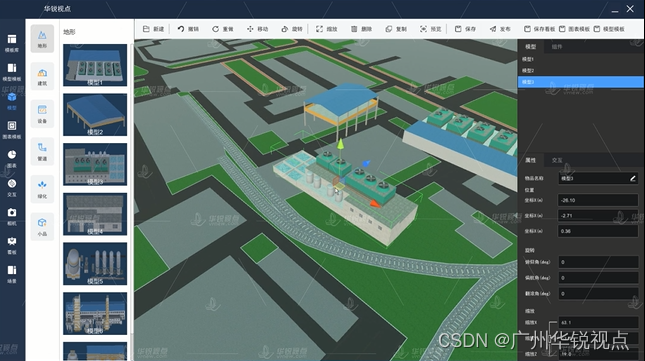
广州华锐互动:数字孪生可视化制作软件有哪些亮点?
由广州华锐互动开发的数字孪生可视化制作软件在当今的数字孪生领域中扮演着重要角色,它突破了许多传统数字孪生可视化制作软件的限制。以下是几个方面的突破: 无限自由度:传统的3D建模工具通常有限制编辑器的自由度,使用户难以进行…...

设计模式之工厂模式讲解与案例
工厂模式是一种创建对象的设计模式,它通过提供一个统一的接口来创建对象,隐藏了具体对象的实例化过程。Java中的工厂模式有多种实现方式,下面我将举两个常见的例子。 简单工厂模式(Simple Factory Pattern):…...
(免费领源码)php#MySQL软件测试文档管理系统28035-计算机毕业设计项目选题推荐
目 录 摘 要 Abstract 第1章 前 言 1.1 研究背景 1.2 开发意义 1.3 系统开发目标 第2章 系统开发环境 6 2.1 HTTP协议 6 2.2 HTML网页技术 6 2.3 B/S结构 6 2.4 PHP脚本语言 7 2.5 MySQL数据库 7 2.6 Apache简介 8 第3章 需求分析 3.1 需求分析 3.2 系统可…...

05.Oracle数据库对象
Oracle数据库对象 Oracle数据库对象是指在Oracle数据库中存储和管理数据的各种实体。以下是一些常见的Oracle数据库对象: 表(Table):用于存储数据的基本结构。表由一组列(Column)组成,每列定义了…...

某国产中间件企业:提升研发安全能力,助力数字化建设安全发展
某国产中间件企业是我国中间件领导者,国内领先的大安全及行业信息化解决方案提供商,为各个行业领域近万家企业客户提供先进的中间件、信息安全及行业数字化产品、解决方案及服务支撑,致力于构建安全科学的数字世界,帮助客户实现…...

Servlet中主要的内置对象
Servlet中有一些内置对象,它们提供了与 Web 容器和客户端交互的功能。这些对象在开发Servlet时可以直接使用,无需显式创建。 一些主要的内置对象包括: HttpServletRequest:代表客户端的HTTP请求,提供访问请求的内容&am…...
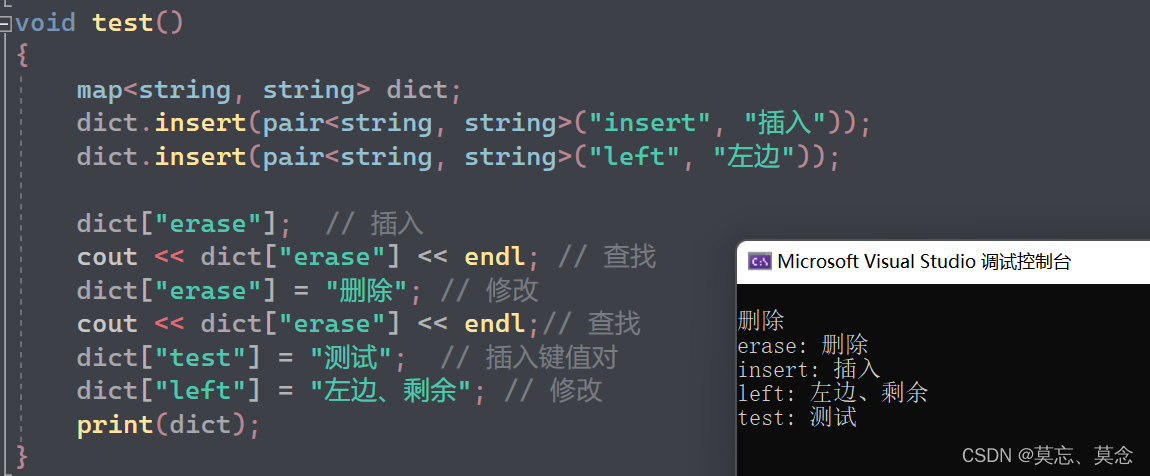
STL-set和map
目录 一、pair和make_pair 1. pair 2. make_pair 二、set (一)set的模板参数列表 (二)set的构造 (三)set的插入 1. 测试1 2. 测试2 (四)low_bound和upper_boundÿ…...

【WinForm详细教程四】WinForm中的ProgressBar 、ImageList和ListView控件
文章目录 1.ProgressBar2. ImageList3.ListView控件 1.ProgressBar 用于显示某个操作的进度。 属性: Value: 表示当前进度条的值,其范围由Min和Max决定。Step: 设置每次调用PerformStep()方法时增加的步长。MarqueeAnimationSpeed: 在Style设置为Marq…...

写一个简单实用的Excel工具类
我们在开发中经常要将数据导入成Excel表格供展示,也需要解析Excel中的数据,官方提供的api操作太麻烦,这边封装了一个Excel工具类,可以很轻松的实现Excel的操作 首先加入依赖 <dependencies><!-- EasyPoi 基本库依赖 --…...
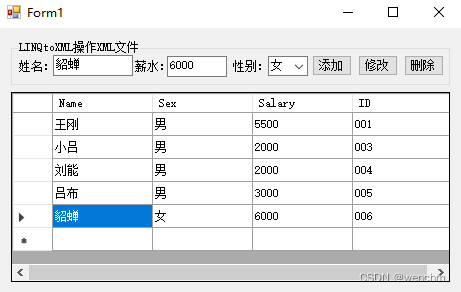
C#中LINQtoObjects、LINQtoDataSet和LINQtoXML
目录 一、使用LINQ操作数组和集合 二、使用LINQ操作DataSet数据集 1.AsEnumerable()方法 2.CopyToDataTable()方法 3.AsDataView()方法 4.Take()方法 5.Sum()方法 6.示例 (1)源码 (2)生成效果 三、使用LINQ操作XML 1.…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...
