0101基础概念-图-数据结构和算法(Java)
文章目录
- 1 图
- 1.1 定义
- 1.2 4种图模型
- 2 无向图
- 2.1 定义
- 2.2 术语
- 后记
1 图
1.1 定义
图是一种非线性的数据结构,表示多对多的关系。
图(Graph)是由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为:G(V, E),其中,G表示一个图,V是图G中顶点的集合,E是图G中边的集合。
在图中需要注意的是:
-
线性表和树可以看做特殊的图。
-
线性表中我们把数据元素叫元素,树中将数据元素叫结点,在图中数据元素,我们则称之为顶点(Vertex)。
-
线性表可以没有元素,称为空表;树中可以没有节点,称为空树;但是,在图中不允许没有顶点(有穷非空性)
-
线性表中的各元素是线性关系,树中的各元素是层次关系,而图中各顶点的关系是用边来表示(边集可以为空)。
1.2 4种图模型
- 无向图
- 有向图
- 加权图
- 加权有向图
2 无向图
2.1 定义
图是由一组顶点和一组能够将两个顶点相连的边组成。
图下图2.1-1所示:

顶点一般使用0至V-1来表示一张含有V个顶点的图中的各个顶点,使用数组索引作为结点很方便。我们使用v-w或者w-v表示连接v和w的边。
特殊的图:
- 自环:一条连接一个顶点和其自身的边
- 连接同一对顶点的两条及以上的边称为平行边
含有平行边的图称为多重图;没有平行边或自环的图称为简单图。
2.2 术语

-
相邻顶点:由同一条边连接的两个顶点,称为相邻顶点,并称这条边依附于这2个顶点。
-
度数:某个顶点的度数即为依附于这个顶点的边的总数。
-
子图:有一幅图所以边的一个子集(以及他们所依附的所有顶点)组成的图。
-
路径:由边顺序连接的一系列顶点。
- 简单路径:一条没有重复顶点的路径。
-
环:一条至少含有一条边且起点和终点相同的路径。
- 简单环:一条(除起点和终点必须相同外)不含有重复顶点和边的环。
- u-v-w-x-u记法表示从u到v到w在回到u到一条环。
-
路径长度或者环的长度:路径或者边所 包含的边数。
-
连通:当两个顶点之间存在一条连接双方的路径时,我们称一个顶点和另外一个顶点连通。
- u-v-w-x记法表示u到x的一条路径
-
连通图:如果从任意一顶点都存在一条路径到达另一个任意顶点,我们称这幅图是连通图。
- 一幅非连通图由若干连通的部分组成,它们都是其极大连通子图(分量)。
-
连通图的生成树:连通图的生成树是它的一幅子图,它含有图中的所有顶点且是一颗树。
- 树是一幅无环连通图。互不相连的树组成的集合称为森林。
-
图的生成树森林:图的所有连通子图上生成树的集合。
一棵树如下图所示:

生成树森林:

当且仅当一幅含有V个结点的图G满足下列5个条件之一时,它就是一棵树:
-
G有V-1条边且不含有环;
-
G有V-1条边且时连通的;
-
G是连通的,但删除任意一条边都会使它不在连通;
-
G是无环图,但添加任意一条边都会产生一条环;
-
G中任意一堆顶点之间仅存在一条简单路径。
-
图密度:图密度是指已连接的顶点对占所有可能连接顶点对的比例。
- 稀疏图:如果一幅图中不同边的数量在顶点总数V的一个小的常数倍以内,那么我们就称这幅图是稀疏的。
- 稠密图:否则就是稠密图。
-
二分图:二分图是一种能够将所有结点分为两部分的图,其中图的每条边所连接的两个顶点分别属于不同的部分。
后记
如果小伙伴什么问题或者指教,欢迎交流。
❓QQ:806797785
⭐️源代码仓库地址:https://gitee.com/gaogzhen/algorithm
参考链接:
[1][美]Robert Sedgewich,[美]Kevin Wayne著;谢路云译.算法:第4版[M].北京:人民邮电出版社,2012.10
[2]数据结构:图的基本概念
相关文章:

0101基础概念-图-数据结构和算法(Java)
文章目录1 图1.1 定义1.2 4种图模型2 无向图2.1 定义2.2 术语后记1 图 1.1 定义 图是一种非线性的数据结构,表示多对多的关系。 图(Graph)是由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为:G(V, E)…...

Linux基础命令和工具使用详解
Linux基础命令和工具使用详解一、grep搜索字符二、find查找文件三、ls 显示文件四、wc命令计算字数五、uptime机器启动时间负载六、ulimit用户资源七、curl http八、scp远程拷贝九、dos2unix和unix2dos十、sed 行处理10.1、简单模式10.2、替换模式十一、awk 列处理11.1、打印某…...

一个好的python文件可以有几种用途?
大家好鸭!我是小熊猫~ 这次来带大家浅浅回顾一点python小知识~ 源码资料电子书:点击此处跳转文末名片获取 python文件总共有两种用途: 一种是执行文件另一种是被当做模块导入 编写好的一个python文件可以有两种用途: 1. 脚本,…...

HDFS优化
单节点多块磁盘数据均衡 生成HDFS块均衡计划 hdfs diskbalancer -plan node1 执行均衡计划,node1.plan.json均衡计划文件 hdfs diskbalancer -execute node1.plan.json 查看当前均衡任务的执行情况 hdfs diskbalancer -query node1 取消均衡任务hdfs diskbalancer -cancel nod…...

行测-判断推理-图形推理-样式规律-黑白运算
黑白元素个数不同,优先考虑黑白运算白白白黑黑白黑白黑选A考试时,这种题不要先把规律全部推出来,再去做题,太慢了直接看要推的图,通过排除法选答案黑白元素个数不同,优先考虑黑白运算白白白黑黑白黑白黑选B…...
java+springboot+vue高校学生医疗保险管理系统
医保管理系统是对与职工健康息息相关的档案进行的系统化、自动化的管理,主要是对职工办理的医疗保险的管理,本系统能够很好的适应社会的需求,最大化的为城镇职工提供服务。医疗保险是国家社会保障体系的重要组成部分,也是社会保险…...

[已解决] AHK 映射 ESC 延迟 500 ms 的严重问题
问题描述 今天发现一个重大bug,我竟然用了一年多都不知道! CapsLock::Esc 我的 ahk 脚本将 capslock 映射为 esc,但这在vim环境中,估算响应 500ms。 也就说按下 caps 键,还要等一会,才进入normal模式 如果…...

QML state详解
1.state简介 changes(list<Change>):保存当前State下的多个Change对象,比如PropertyChanges、StateChangeScript、ParentChange等。 extend(string):表示该状态要在哪个State的基础上进行扩展,当一个…...

一起Talk Android吧(第五百零六回:如何调整组件在约束布局中的角度)
文章目录背景介绍相关属性使用方法示例程序各位看官们大家好,上一回中咱们说的例子是"如何调整组件在约束布局中的大小",这一回中咱们说的例子是"如何调整组件在约束布局中的角度"。闲话休提,言归正转, 让我们一起Talk A…...
微信投票-课后程序(JAVA基础案例教程-黑马程序员编著-第七章-课后作业)
【实验7-5】 微信投票 【任务介绍】 1.任务描述 如今微信聊天已经普及到几乎每一个人,在聊天中,经常会有人需要帮忙在某个APP中投票。本案例要求编写一个模拟微信投票的程序,通过在控制台输入指令,实现添加候选人、查看当前投票…...

duboo+zookeeper分布式架构入门
分布式 dubbo Zookeeper 分布式系统就是若干独立计算机的集合(并且这些计算机之间相互有关联,就像是一台计算机中的C盘F盘等),这些计算对于用户来说就是一个独立的系统。 zookeeper安装 下载地址:Index of /dist/z…...

黑盒测试用例设计方法-等价类划分法
目录 一、等价类的作用 二、等价类的分类 三、等价类的方法 四、等价类的原则 五、按照测试用例的完整性划分等价类 六、等价类步骤 七、案例 一、等价类的作用 为穷举测试设计测试点。 穷举:列出所有的可能情况,对其一一判断。 测试点&#x…...

4.OCR文本识别Connectionist Temporal Classification(CTC)算法
文章目录1.基础介绍2.Connectionist Temporal Classification(CTC)算法2.1 什么是Temporal Classification2.2 CTC问题描述2.2关于对齐2.3 前向后向算法2.4 推理时3.pytorch中的CTCLOSS参考资料欢迎访问个人网络日志🌹🌹知行空间🌹dz…...

误删了Ubuntu/Linux的一些默认用户目录怎么办?
用户目录:指位于 $HOME 下的一系列常用目录,例如 Documents,Downloads,Music,还有 Desktop等。本文不是讲如何恢复原有目录及其重要文件,适用于仅恢复目录功能一:仅恢复个别目录如误删了Desktop…...
ArXiv简介以及论文提交
arXiv网站简介 arXiv是一个收集物理学、数学、计算机科学、生物学与数理经济学的论文预印本的网站。其中arXiv发音同“archive”,因为“X”代表希腊字母 ,国际音标为[kai]。它于1991年8月14日成立,现由美国康奈尔大学维护。 ——维基百科 对…...

pytorch学习
目录如下: pytorch常用操作 pytorch 常用操作 pytorch 的 detach()函数 1. 什么是detach()函数 我们在将输出特征矩阵进行存储的时候,经常需要将torch.Tensor类型的数据转换成别的如numpy类型的数据,但是Tensor类型的数据是会自动计算梯度…...
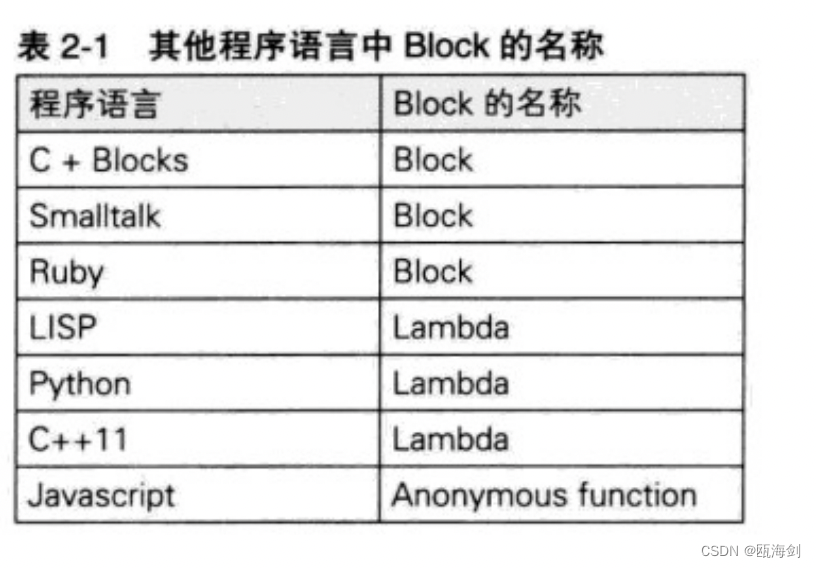
【OC】块初识
Block简介 Blocks是C语言的扩充功能。可以用一句话来表示Blocks的扩充功能:带有自动变量的匿名函数。 匿名函数 所谓匿名函数就是不带有名称的函数。C语言的标准不允许存在这样的函数。例: int func(int count);它声明了名称为func的函数。下面的源代…...
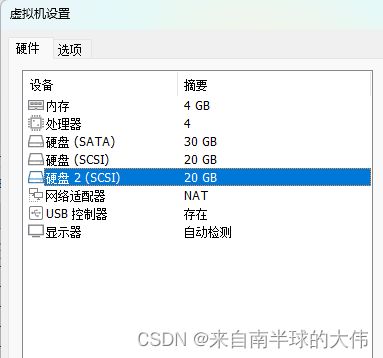
3-2 创建一个至少有两个PV组成的大小为20G的名为testvg的VG
文章目录1. 在vmware添加多块20G的硬盘,并创建分区2. 创建一个至少有两个PV组成的大小为20G的名为testvg的VG,要求PE大小为16M,而后在卷组中创建大小为5G的逻辑卷testlv;挂载至/users目录3. 新建用户archlinux,要求其家目录为/users/archlinu…...

【密码学】 一篇文章讲透数字证书
【密码学】 一篇文章讲透数字证书 数字证书介绍 数字证书是一种用于认证网络通信中参与者身份和加密通信的证书,人们可以在网上用它来识别对方的身份。 我们在上一篇博客中介绍了数字签名的作用和原理,数字签名可以防止消息被否认。有了公钥算法和数字签…...
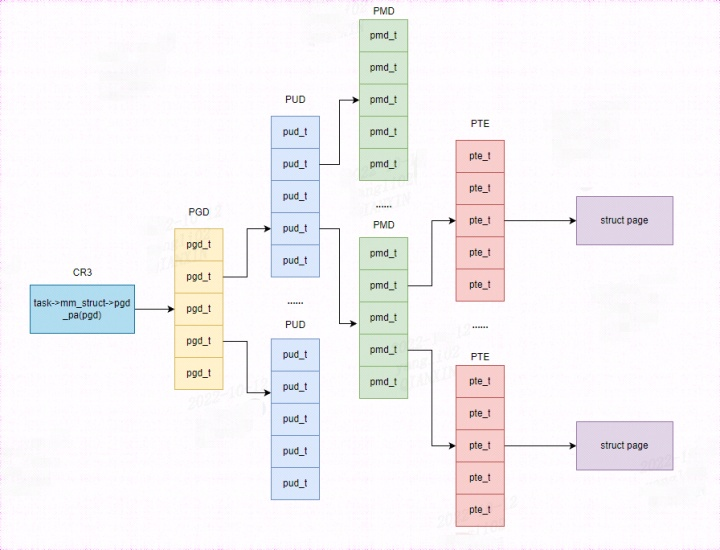
Linux 操作系统原理 — 内存管理 — 虚拟地址空间(x86 64bit 系统)
目录 文章目录目录虚拟地址格式与内核页表(四级页表)虚拟地址格式与内核页表(四级页表) 在 x86 64bit 系统中,可以描述的最长地址空间为 2^64(16EB),远远超过了目前主流内存卡的规格…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...

从实验室到产业:IndexTTS 在六大核心场景的落地实践
一、内容创作:重构数字内容生产范式 在短视频创作领域,IndexTTS 的语音克隆技术彻底改变了配音流程。B 站 UP 主通过 5 秒参考音频即可克隆出郭老师音色,生成的 “各位吴彦祖们大家好” 语音相似度达 97%,单条视频播放量突破百万…...
