动手学深度学习:2.线性回归pytorch实现
动手学深度学习:2.线性回归pytorch实现
- 1.手动构造数据集
- 2.小批量读取数据集
- 3.定义模型和损失函数
- 4.初始化模型参数
- 5.小批量随机梯度下降优化算法
- 6.训练
- 完整代码
- Q&A
1.手动构造数据集
import torch
from torch.utils import data
from d2l import torch as d2ltrue_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = d2l.synthetic_data(true_w, true_b, 1000)
使用 d2l.torch.synthetic_data() 函数生成 y = X w + b + n o i s e y = Xw + b + noise y=Xw+b+noise 数据集。
2.小批量读取数据集
可以调用框架中现有的API来读取数据。 我们将features和labels作为API的参数传递,并通过数据迭代器指定batch_size。
布尔值is_train表示是否希望数据迭代器对象在每个迭代周期内打乱数据。
def load_array(data_arrays, batch_size, is_train=True): """构造一个PyTorch数据迭代器"""dataset = data.TensorDataset(*data_arrays)return data.DataLoader(dataset, batch_size, shuffle=is_train)batch_size = 10
data_iter = load_array((features, labels), batch_size)
构造的 data_iter 数据迭代器使用方法,同 线性回归从0开始实现 中的使用相同。
为了验证是否正常工作,让我们读取并打印第一个小批量样本:这里我们使用iter构造Python迭代器,并使用next从迭代器中获取第一项
next(iter(data_iter))
'''
[tensor([[ 0.5050, -1.7171],[ 0.8045, -1.2517],[-0.4567, 0.2793],[-0.8896, -0.4969],[ 1.6303, 0.1123],[ 2.5058, -0.0823],[-0.3293, -1.2887],[-0.9669, -1.8388],[-0.1570, -0.6264],[ 1.0302, 1.2225]]),
tensor([[11.0521],[10.0705],[ 2.3309],[ 4.1006],[ 7.0623],[ 9.4687],[ 7.9316],[ 8.5144],[ 6.0212],[ 2.1108]])]
'''
3.定义模型和损失函数
对于标准深度学习模型,我们可以使用框架的预定义好的层。这使我们只需关注使用哪些层来构造模型,而不必关注层的实现细节。
我们首先定义一个模型变量net,它是一个Sequential类的实例。 Sequential类将多个层串联在一起。 当给定输入数据时,Sequential实例将数据传入到第一层, 然后将第一层的输出作为第二层的输入,以此类推。
在下面的例子中,我们的模型只包含一个层,因此实际上不需要Sequential。 但是由于以后几乎所有的模型都是多层的,在这里使用Sequential会让你熟悉“标准的流水线”。
全连接层 fully-connected layer ,在PyTorch中,全连接层在Linear类中定义。
我们将两个参数传递到nn.Linear中。 第一个指定输入特征形状,即2,第二个指定输出特征形状,输出特征形状为单个标量,因此为1。
from torch import nnnet = nn.Sequential(nn.Linear(2, 1))
计算均方误差使用的是MSELoss类,也称为平方 L 2 L_2 L2 范数。 默认情况下,它返回所有样本损失的平均值。
loss = nn.MSELoss()
4.初始化模型参数
在使用net之前,我们需要初始化模型参数。 如在线性回归模型中的权重和偏置。 深度学习框架通常有预定义的方法来初始化参数。 在这里,我们指定每个权重参数应该从均值为0、标准差为0.01的正态分布中随机采样, 偏置参数将初始化为零。
正如我们在构造nn.Linear时指定输入和输出尺寸一样, 现在我们能直接访问参数以设定它们的初始值。我们通过net[0]选择网络中的第一个图层, 然后使用weight.data和bias.data方法访问参数。 我们还可以使用替换方法normal_和fill_来重写参数值。
net[0].weight.data.normal_(0, 0.01)
net[0].bias.data.fill_(0)
5.小批量随机梯度下降优化算法
小批量随机梯度下降算法是一种优化神经网络的标准工具, PyTorch在optim模块中实现了该算法的许多变种。
当我们实例化一个SGD实例时,我们要指定优化的参数 (可通过net.parameters()从我们的模型中获得)以及优化算法所需的超参数字典。 小批量随机梯度下降只需要设置lr值,这里设置为0.03。
trainer = torch.optim.SGD(net.parameters(), lr=0.03)
可以参考 线性回归从0开始实现 中的 sgd 函数的实现。
6.训练
在每个迭代周期里,我们将完整遍历一次数据集(train_data), 不停地从中获取一个小批量的输入和相应的标签。 对于每一个小批量,我们会进行以下步骤:
- 通过调用
net(X)生成预测并计算损失l(前向传播)。 - 通过进行反向传播来计算梯度。
- 通过调用优化器来更新模型参数。
num_epochs = 3
for epoch in range(num_epochs):for X, y in data_iter:l = loss(net(X) ,y)trainer.zero_grad() # 在默认情况下,PyTorch会累积梯度,我们需要清除之前的值l.backward()trainer.step()l = loss(net(features), labels)print(f'epoch {epoch + 1}, loss {l:f}')'''
epoch 1, loss 0.000354
epoch 2, loss 0.000104
epoch 3, loss 0.000104
'''
下面我们比较生成数据集的真实参数和通过有限数据训练获得的模型参数。要访问参数,我们首先从net访问所需的层,然后读取该层的权重和偏置。
w = net[0].weight.data
print('w的估计误差:', true_w - w.reshape(true_w.shape))
b = net[0].bias.data
print('b的估计误差:', true_b - b)'''
w的估计误差: tensor([-8.0824e-05, 4.2796e-04])
b的估计误差: tensor([-0.0006])
'''
完整代码
import torch
from torch.utils import data
from d2l import torch as d2l
from torch import nntrue_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = d2l.synthetic_data(true_w, true_b, 1000)def load_array(data_arrays, batch_size, is_train=True):"""构造一个PyTorch数据迭代器"""dataset = data.TensorDataset(*data_arrays)return data.DataLoader(dataset, batch_size, shuffle=is_train)batch_size = 10
data_iter = load_array((features, labels), batch_size)
print(next(iter(data_iter)))net = nn.Sequential(nn.Linear(2, 1))
net[0].weight.data.normal_(0, 0.01)
net[0].bias.data.fill_(0)loss = nn.MSELoss(reduction='sum')
trainer = torch.optim.SGD(net.parameters(), lr=0.03 / batch_size)num_epochs = 3
for epoch in range(num_epochs):for X, y in data_iter:l = loss(net(X), y)trainer.zero_grad()l.backward()trainer.step()l = loss(net(features), labels)print(f'epoch {epoch + 1}, loss {l:f}')w = net[0].weight.data
print('w的估计误差:', true_w - w.reshape(true_w.shape))
b = net[0].bias.data
print('b的估计误差:', true_b - b)
Q&A
如果将小批量的总损失替换为小批量损失的平均值,需要如何更改学习率?
如果我们用
nn.MSELoss(reduction=‘sum’)替换nn.MSELoss()为了使代码的行为相同,需要怎么更改学习速率?为什么?
查看损失函数 nn.MSELoss 定义可知,损失默认为 mean
def __init__(self, size_average=None, reduce=None, reduction: str = 'mean') -> None:super().__init__(size_average, reduce, reduction)
当使用 nn.MSELoss(reduction=‘sum’) 时,要把学习率除以batch_size才能达到 nn.MSELoss() 同样的效果。因为在求导过程中,常数项作为系数保持不变,梯度的大小也乘上了batch_size。
loss = nn.MSELoss(reduction='sum')trainer = torch.optim.SGD(net.parameters(), lr=0.03/batch_size)
修改前的运行效果:
epoch 1, loss 0.000354
epoch 2, loss 0.000104
epoch 3, loss 0.000104
w的估计误差: tensor([-8.0824e-05, 4.2796e-04])
b的估计误差: tensor([-0.0006])
修改以后运行效果:
epoch 1, loss 0.220722
epoch 2, loss 0.110026
epoch 3, loss 0.109946
w的估计误差: tensor([0.0008, 0.0002])
b的估计误差: tensor([9.3937e-05])
相关文章:

动手学深度学习:2.线性回归pytorch实现
动手学深度学习:2.线性回归pytorch实现 1.手动构造数据集2.小批量读取数据集3.定义模型和损失函数4.初始化模型参数5.小批量随机梯度下降优化算法6.训练完整代码Q&A 1.手动构造数据集 import torch from torch.utils import data from d2l import torch as d2l…...

重要的linux指令
系统管理命令 切换用户 su 用户名管理员身份运行 sudo 命令实时显示进程信息(linux下任务管理器) top查看进程信息(ps) ps -efps -ef | grep 进程名 ps -aux | grep 进程名参数说明e 显示所有进程f 全格式a 显示所有程序u 以用户为主的格式来显示程序状况x 显示无控制终端…...

delphi7安装并使用皮肤控件
1、下载控件 我已经上传到云盘,存储位置 2、下载后并解压。 3、打开dephi7,File-Open,打开路径D:\LC\Desktop\vclskin2_XiaZaiBa\d7, 然后将 D:\LC\Desktop\vclskin2_XiaZaiBa\d7文件夹中所有后缀.dcu的文件复制粘贴到delphi安装路…...

安徽省黄山景区免9天门票为哪般?
今日浑浑噩噩地睡了大半天,强撑起身子写网文......可是,题材不好选,本“人民体验官”只得推广人民日报官方微博文化产品《这两个月“黄山每周三免门票”》。 图:来源“人民体验官”推广平台 因年事渐高,又有未愈的呼吸…...
MFC 窗体插入图片
1.制作BMP图像1.bmp 放到res文件夹下,资源视图界面导入res文件夹下的1.bmp 2.添加控件 控件类型修改为Bitmap 图像,选择IDB_BITMAP1 3.效果...

关于中间件技术
中间件是一种独立的系统软件或服务程序,可以帮助分布式应用软件在不同的技术之间共享资源。中间件可以: 1、负责客户机与服务器之间的连接和通信,以及客户机与应用层之间的高效率通信机制。 2、提供应用的负载均衡和高可用性、安全机制与管…...
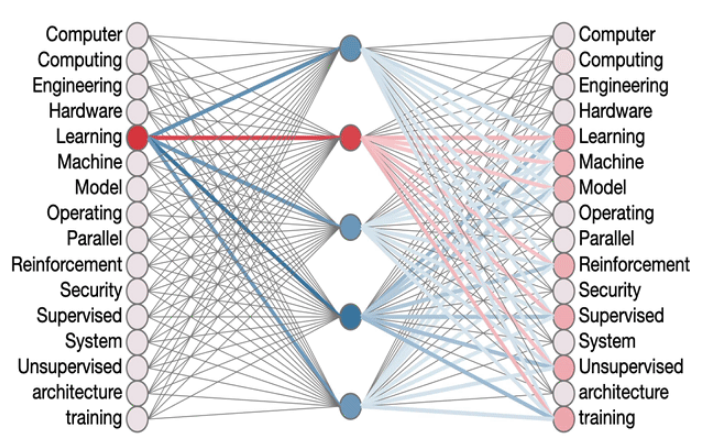
机器学习中的嵌入:释放表征的威力
简介 机器学习通过使计算机能够从数据学习和做出预测来彻底改变了人工智能领域。机器学习的一个关键方面是数据的表示,因为表示形式的选择极大地影响了算法的性能和有效性。嵌入已成为机器学习中的一种强大技术,提供了一种捕获和编码数据点之间复杂关系的…...
【Midjourney入门教程3】写好prompt常用的参数
文章目录 1、图片描述词(图片链接)文字描述词后缀参数2、权重划分3、后缀参数版本选择:--v版本风格:--style长宽比:--ar多样性: --c二次元化:--niji排除内容:--no--stylize--seed--tile、--q 4、…...
01-单节点部署clickhouse及简单使用
1、下载rpm安装包: 官网:https://packages.clickhouse.com/rpm/stable/ clickhouse19.4版本之后只需下载3个rpm安装包,上传到节点目录即可 2、rpm包安装: 安装顺序为conmon->server->client 执行 rpm -ivh ./clickhouse-…...
项目实战:展示第一页数据
1、在FruitDao接口中添加查询第一页数据和查询总记录条数 package com.csdn.fruit.dao; import com.csdn.fruit.pojo.Fruit; import java.util.List; //dao :Data Access Object 数据访问对象 //接口设计 public interface FruitDao {void addFruit(Fruit fruit);vo…...

c#中使用METest单元测试
METest是一个用于测试C#代码的单元测试框架。单元测试是一种软件测试方法,用于验证代码的各个单元(函数、方法、类等)是否按照预期工作。METest提供了一种简单而强大的方式来编写和运行单元测试。 TestMethod:这是一个特性&#…...

七月论文审稿GPT第二版:从Meta Nougat、GPT4审稿到Mistral、LLaMA LongLora
前言 如此前这篇文章《学术论文GPT的源码解读与微调:从chatpaper、gpt_academic到七月论文审稿GPT》中的第三部分所述,对于论文的摘要/总结、对话、翻译、语法检查而言,市面上的学术论文GPT的效果虽暂未有多好,可至少还过得去&am…...

社群团购对接合作,你有研究过社群团购平台的选品吗?
社群团购对接合作,你有研究过社群团购平台的选品吗? 社群团购选品是非常重要的一项工作,一个好的社群团购平台选品逻辑包含了:用户定位,时节性,产品性价比,售后率。用户定位在选品过程中非常重要…...
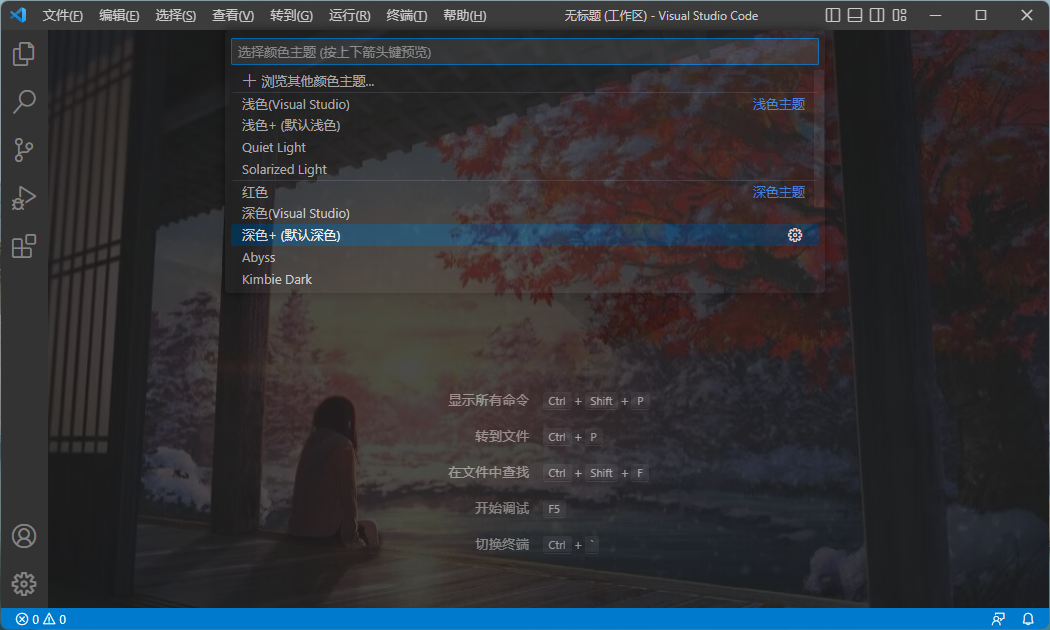
VSCode 如何设置背景图片
VSCode 设置背景图片 1.打开应用商店,搜索 background ,选择第一个,点击安装。 2. 安装完成后点击设置,点击扩展设置。 3.点击在 settings.json 中编辑。 4.将原代码注释后,加入以下代码。 // { // "workben…...
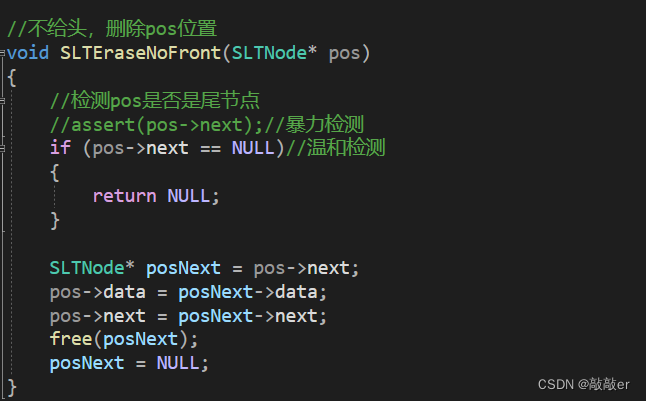
【数据结构】单向链表的增删查改以及指定pos位置的插入删除
目录 单向链表的概念及结构 尾插 头插 尾删 编辑 头删 查找 在pos位置前插 在pos位置后插 删除pos位置 删除pos的后一个位置 总结 代码 单向链表的概念及结构 概念:链表是一种 物理存储结构上非连续 、非顺序的存储结构,数据元素的 逻辑顺序 是…...

PageRank算法c++实现
首先用邻接矩阵A表示从页面j到页面i的概率,然后根据公式生成转移概率矩阵 M(1-d)*Qd*A 常量矩阵Q(qi,j),qi,j1/n 给定点击概率d,等级值初始向量R0,迭代终止条件e; 计算Ri1M*R…...
超低价:阿里云双11服务器优惠价格表_87元一年起
2023阿里云双十一优惠活动已经开启了,轻量2核2G服务器3M带宽优惠价87元一年、2核4G4M带宽优惠价165元一年,云服务器ECS经济型e实例2核2G3M固定带宽优惠价格99元一年,还有2核4G、2核8G、4核8G、4核16G、8核32G等配置报价,云服务器e…...

docker的安装Centos8
在CentOS 7中,可以使用yum安装Docker。Docker官方提供了一个yum源,可以用于安装Docker。以下是安装Docker的步骤: 卸载旧版本的Docker(如果有) 如果你之前安装过Docker,需要先卸载旧版本的Docker。执行以…...

Android.mk文件制定了链接库,但是出现ld Error
问题描述 Android.mk文件中,指定了库: LOCAL_LDLIBS : -lmylib LOCAL_LDFLAGS -L$(MYLIB_DIR)/lib出现ld: error: undefined symbol: my_function,于是查看so里面是否有my_function函数: nm -D libmylib.so | grep my_functio…...
10.MySQL事务(上)
个人主页:Lei宝啊 愿所有美好如期而遇 目录 前言: 是什么? 为什么? 怎么做? 前言: 本篇文章将会说明什么是事务,为什么会出现事务?事务是怎么做的? 是什么? 我…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

CppCon 2015 学习:REFLECTION TECHNIQUES IN C++
关于 Reflection(反射) 这个概念,总结一下: Reflection(反射)是什么? 反射是对类型的自我检查能力(Introspection) 可以查看类的成员变量、成员函数等信息。反射允许枚…...

中国政务数据安全建设细化及市场需求分析
(基于新《政务数据共享条例》及相关法规) 一、引言 近年来,中国政府高度重视数字政府建设和数据要素市场化配置改革。《政务数据共享条例》(以下简称“《共享条例》”)的发布,与《中华人民共和国数据安全法》(以下简称“《数据安全法》”)、《中华人民共和国个人信息…...
